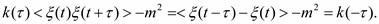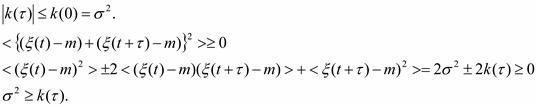Автокорреляционная функция (АКФ) и ее свойства. Частная автокорреляционная функция (ЧАКФ) и ее свойства

Автокорреляционной функцией называется функция оценки коэффициента автокорреляции в зависимости от величины временного лага между исследуемыми рядами.

Графически автокорреляционная функция изображается с помощью коррелограммы. Коррелограмма отражает численно и графически коэффициенты автокорреляции и их стандартные ошибки для последовательности лагов из определённого диапазона (например, от 1 до 25). При этом по оси Х откладываются значения τ (тау) – величины сдвига между рядами остатков, которые совпадают с порядком автокорреляционного коэффициента. Также на коррелограмме отмечается диапазон в размере двух стандартных ошибок коэффициентов автокорреляции на каждом лаге.

Частная автокорреляционная функция является более углублённой версией обычной автокорреляционной функции. Её отличительной особенностью является исключение корреляционной зависимости между наблюдениями внутри лагов, т. е. частная автокорреляционная функция на каждом лаге отличается от обычной автокорреляционной функции на величину удалённых автокорреляций с меньшими временными лагами. Следовательно, частная автокорреляционная функция более точно характеризует автокорреляционные зависимости внутри временного ряда.

Свойства автокорреляционной функции:

1) чётность (определяется как k()=k(-))

2) Абсолютное значение автокорреляционной функции при любых не может превышать её значения при =0.

3) Для многих практических стационарных процессов справедливо:

Источник

КОРРЕЛЯЦИЯ СИГНАЛОВ

Предельный страх и предельный пыл храбрости одинаково расстраивают желудок и вызывают понос.

Мишель Монтень. Французский юрист-мыслитель, XVI в.

Вот это номер! Две функции имеют стопроцентную корреляцию с третьей и ортогональны друг другу. Ну и шуточки были у Всевышнего при сотворении Мира.

Анатолий Пышминцев. Новосибирский геофизик Уральской школы, ХХ в.

8.2. Взаимнокорреляционные функции сигналов (ВКФ).

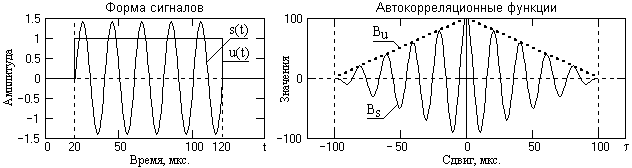
Корреляция (correlation), и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов. Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы «прикладываем» искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения.

Корреляционный анализ дает возможность установить в сигналах (или в рядах цифровых данных сигналов) наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).

В варианте автокорреляции (autocorrelation) по аналогичной методике производится определение скалярного произведения сигнала s(t) с собственной копией, скользящей по аргументу. Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчетов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.

Особое значение методы корреляции имеют при анализе случайных процессов для выявления неслучайных составляющих и оценки неслучайных параметров этих процессов.

Заметим, что в терминах «корреляция» и «ковариация» в настоящее время существует изрядная путаница. В иностранной литературе термин «ковариация» применяется к центрированным функциям, а «корреляция» – к произвольным. В отечественной литературе, и особенно в литературе по сигналам и их обработке, довольно часто применяется прямо противоположная терминология. Однако при переводах иностранной литературы терминология, как правило, не изменяется, и начинает все шире проникать в отечественную литературу. Принципиального значения это не имеет, но при знакомстве с литературными источниками стоит обращать внимание на принятое назначение данных терминов.

При разработке настоящих лекций было принято решение использовать общепринятую международную терминологию, как согласованную по понятиям с основными положениями теории вероятностей и математической статистики.

8.1. Автокорреляционные функции сигналов [1,25].

Понятие автокорреляционных функций (АКФ) сигналов. АКФ (correlation function, CF) сигнала s(t), конечного по энергии, является количественной интегральной характеристикой формы сигнала, и определяется интегралом от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t :

B s ( t ) =s(t) s(t+ t ) dt = б s(t), s(t+ t ) с = ||s(t)|| ||s(t+ t )|| cos j ( t ). (8.1.1)

АКФ относится к четным функциям, в чем нетрудно убедиться заменой переменной t = t- t в выражении (8.1.1):

B s ( t ) = s(t) s(t+ t ) dt = s(t- t ) s(t) dt = B s (- t ).

Максимум АКФ, равный энергии сигнала при t =0, всегда положителен, а модуль АКФ при любом значении временного сдвига не превосходит энергии сигнала. Последнее прямо вытекает из свойств скалярного произведения (как и неравенство Коши-Буняковского):

б s(t), s(t+ t ) с = ||s(t)|| Ч ||s(t+ t) || Ч cos j ( t ),

B s ( t ) = s(t) s(t- t ) dt. (8.1.1′)

По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается, а, соответственно, косинус угла взаимодействия и скалярное произведение в целом стремятся к нулю:

= 0.

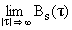
АКФ, вычисленная по центрированному значению сигнала s(t), представляет собой автоковариационную функцию сигнала:

C s ( t ) =[s(t)- m s ][s(t+ t )- m s ] dt, (8.1.2)

где m s – среднее значение сигнала. Ковариационные функции связаны с корреляционным функциями достаточно простым соотношением:

B s ( t ) =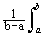s(t) s(t+ t ) dt. (8.1.3)

АКФ может быть вычислена и для слабозатухающих сигналов с бесконечной энергией, как среднее значение скалярного произведения сигнала и его копии при устремлении интервала задания сигнала к бесконечности:

B s ( t ) = 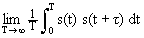. (8.1.4)

АКФ по данным выражениям имеет физическую размерность мощности, и равна средней взаимной мощности сигнала и его копии в функциональной зависимости от сдвига копии.

Иногда эту функцию называют «истинной» автокорреляционной функцией. В силу нормировки ее значения не зависят от единиц (масштаба) представления значений сигнала s(t) и характеризуют степень линейной связи между значениями сигнала в зависимости от величины сдвига t между отсчетами сигнала. Так, например, для шумовых сигналов при полной статистической независимости отсчетов по независимой переменной, значение r s ( t ) стремится к нулю при t ≠ 0, и стремится к 1 при t ® 0.

АКФ периодических сигналов. Энергия периодических сигналов бесконечна, поэтому АКФ периодических сигналов вычисляется по одному периоду Т, с усреднением скалярного произведения сигнала и его сдвинутой копии в пределах этого периода:

B s ( t ) = (1/Т) 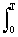s(t) s(t- t ) dt. (8.1.7)

Математически более строгое выражение:

B s ( t ) = 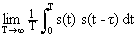. (8.1.8)

При t =0 значение нормированной на период АКФ равно средней мощности сигналов в пределах периода. При этом АКФ периодических сигналов является периодической функцией с тем же периодом Т. Так, для сигнала s(t) = A cos( w 0 t+ j 0 ) при T=2 p / w 0 имеем:

B s ( t ) = 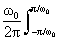A cos( w 0 t+ j 0 ) A cos( w 0 (t- t )+ j 0 ) = (A 2 /2) cos( w 0 t ).

Полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ. С помощью функций автокорреляции можно проверять наличие периодических свойств в любых произвольных сигналах.

АКФ дискретных сигналов. При интервале дискретизации данных D t = const вычисление АКФ выполняется по интервалам Dt = D t и обычно записывается, как дискретная функция номеров n сдвига отсчетов n Dt :

Дискретные сигналы обычно задаются в виде числовых массивов определенной длины с нумерацией отсчетов к = 0,1,…N, а вычисление дискретной АКФ выполняется в одностороннем варианте с учетом длины массивов по формуле:

Множитель N/(N+1-n) в данной функции является поправочным коэффициентом на постепенное уменьшение числа перемножаемых и суммируемых значений (от N до N-n) по мере увеличения сдвига n. Без этой поправки для нецентрированных сигналов в значениях АКФ появляется тренд суммирования средних значений.

Практически, дискретная АКФ имеет такие же свойства, как и непрерывная АКФ. Она также является четной, а ее значение при n = 0 равно мощности дискретного сигнала.

Кодовые сигналы являются разновидностью дискретных сигналов. На определенном интервале кодового слова М Ч D t они могут иметь только два амплитудных значения: 0 и 1 или 1 и –1. При выделении кодов на существенном уровне шумов форма АКФ кодового слова имеет особое значение. С этой позиции наилучшими считаются такие коды, значения боковых лепестков АКФ которых минимальны по всей длине интервала кодового слова при максимальном значении центрального пика. К числу таких кодов относится код Баркера, приведенный в таблице 8.1. Как видно из таблицы, амплитуда центрального пика кода численно равна значению М, при этом амплитуда боковых осцилляций при n № 0 не превышает 1.

Источник

Акф Что Это Такое

Ингибиторы акф препараты

Из данной статьи вы узнаете: что такое ингибиторы АПФ (сокращенно иАПФ), каким образом они понижают давление? Чем похожи и чем различаются друг от друга фармацевтические средства.

Перечень фаворитных препаратов, показания к применению, механизм деяния, побочные эффекты и противопоказания ингибиторов АПФ.

Ингибиторами АПФ именуют группу фармацевтических препаратов, которые заблокируют хим вещество, способствующее сужению сосудов и увеличению давления.

Почки человека продуцируют специфичный фермент – ренин, с которого начинается цепочка хим перевоплощений, приводящих к возникновению в тканях и плазме крови (внутренней средой организма человека и животных) вещества под заглавием «ангиотензинпревращающий фермент», либо ангиотензин.

Что такое ангиотензин? Это фермент, который владеет свойством сузивать сосудистые стены, усиливая тем скорость кровотока (тока внутренней среды организма) и давление.

Сразу его повышение в крови (внутренней средой организма человека и животных) провоцирует выработку надпочечниками остальных гормонов, которые задерживают ионы натрия в тканях, усиливают спазм сосудов, провоцируют сердцебиение, наращивают количество воды в организме.

Выходит замкнутый круг хим перевоплощений, в итоге которого артериальная гипертензия становится устойчивой и содействует повреждению сосудистых стен, развитию приобретенной сердечной и почечной дефицитности.

Ингибитор АПФ (иАПФ) прерывает эту цепочку реакций, заблокируя ее на шаге трансформации в ангиотензинпревращающий фермент.

Сразу он содействует скоплению другого вещества (брадикинина), которое предупреждает развитие патологических клеточных реакций при сердечно-сосудистой и почечной дефицитности (интенсивное деление, рост и отмирание клеток миокарда, почек, сосудистых стен).

Потому иАПФ используют не только лишь для исцеления артериальной гипертензии, да и для профилактики сердечной и почечной дефицитности, инфаркта миокарда, инфаркта.

ИАПФ – одни из самых действенных гипотензивных средств. В отличие от остальных препаратов, которые расширяют сосуды, они предупреждают сосудистый спазм и действуют мягче.

Ингибиторы АПФ назначает врач-терапевт, исходя из симптомов артериальной гипертензии и сопутствующих болезней. Без помощи других принимать и устанавливать суточную дозу не советуют.

Чем различаются иАПФ друг от друга

ИАПФ имеют схожие показания и противопоказания, механизм деяния, побочные эффекты, но различаются друг от друга:

Начальное вещество

Начальное вещество влияет на сроки деяния лекарства в организме, при предназначении это дозволяет подобрать дозу и найти просвет времени, через который нужно повторять прием.

Автокорреляционная функция Примеры расчётов

Санкт-Петербургский институт машиностроения

по дисциплине Статистика

Автокорреляционная функция. Примеры расчётов

Глава 1. Теоретические сведения. 5

Коэффициент автокорреляции и его оценка. 5

Автокорреляционные функции. 7

Аспект Дарбина-Уотсона. 9

Глава 2. Примеры практических расчетов при помощи макроса Excel «Автокорреляционная функция». 11

Пример 1. ВВП (Валовой внутренний продукт — макроэкономический показатель, отражающий рыночную стоимость всех конечных товаров и услуг, то есть предназначенных для непосредственного употребления, произведённых за год во всех отраслях экономики на территории государства) РФ (Российская Федерация — государство в Восточной Европе и Северной Азии, наша Родина).. 11

Пример 2. Импорт. 15

Пример 3. Экспорт. 18

Введение

Повторяющаяся зависимость представляет собой общий тип компонент временного ряда.

Можно просто созидать, что каждое наблюдение весьма похоже на примыкающее; добавочно, имеется циклическая повторяющаяся составляющая, это значит, что каждое наблюдение также похоже на наблюдение, имевшееся в том же самое время период вспять.

В общем, повторяющаяся зависимость быть может формально определена как корреляционная зависимость порядка k меж каждым i-м элементом ряда и (i-k)-м элементом. Ее можно измерить при помощи автокорреляции (т.е.

корреляции меж самими членами ряда); k обычно именуют лагом (время от времени употребляют эквивалентные определения: сдвиг, запаздывание). Если ошибка измерения не очень большая, то периодичность можно найти зрительно, рассматривая поведение членов ряда через любые k временных единиц [7, 153].

Повторяющиеся составляющие временного ряда могут быть найдены при помощи коррелограммы.

Коррелограмма (автокоррелограмма) указывает численно и графически автокорреляционную функцию (AКФ), другими словами коэффициенты автокорреляции для последовательности лагов из определенного спектра.

На коррелограмме обычно отмечается спектр в размере 2-ух обычных ошибок на любом лаге, но обычно величина автокорреляции наиболее увлекательна, чем ее надежность, поэтому что энтузиазм в главном представляют весьма мощные[1] автокорреляции [6, 207].

При исследовании коррелограмм следует держать в голове, что автокорреляции поочередных лагов формально зависимы меж собой. Разглядим последующий пример.

Если 1-ый член ряда тесновато связан со вторым, а 2-ой с третьим, то 1-ый элемент должен также каким-то образом зависеть от третьего и т.д.

Это приводит к тому, что повторяющаяся зависимость может значительно поменяться опосля удаления автокорреляций первого порядка, (т.е. опосля взятия разности с лагом 1).

1. Отдать главные теоретические сведения

2. Отдать примеры расчета АКФ

Для полной свойства случайного процесса недостаточно его математического ожидания и дисперсии. Еще в 1927 г. Е.Е.

Слуцкий ввел для зависимых наблюдений понятие «связанного ряда»: возможность появления на определенном месте тех либо других определенных значений зависит от того, какие значения случайная величина уже получила ранее либо будет получать позднее.

Другими словами, существует поле рассеяния пар значений x(t), x(t+k) временного ряда, где k — неизменный интервал либо задержка, характеризующее взаимозависимость следующих реализаций процесса от прошлых. Теснота данной связи оценивается коэффициентами автоковариации –

g (k) = E[(x(t) — m)(x(t + k) — m)] –

где m и D — математическое ожидание и дисперсия случайного процесса. Для расчета автоковариации и автокорреляции настоящих действий нужна информация о совместном распределении вероятностей уровней ряда p(x(t1),x(t2)).

Так как дисперсия стационарного процесса в хоть какой момент времени (как в t, так и в t + k) равна D = g (0), то автокорреляция с задержкой k быть может выражена как [5, 312]

откуда вытекает, что r (0) = 1. В тех же критериях стационарности коэффициент корреляции r (k) меж 2-мя значениями временного ряда зависит только от величины временного интервала k и не зависит от самих моментов наблюдений t. [2]

В статистике есть некоторое количество выборочных оценок теоретических значений автокорреляции r (k) процесса по конечному временному ряду из n наблюдений. Более пользующейся популярностью оценкой является нециклический коэффициент автокорреляции с задержкой k (Андерсон, 1976; Вайну, 1977):

Распределение коэффициентов автокорреляции непонятно, позтому для оценки их достоверности время от времени употребляют непараметрическую теорию Андерсона (1976), предложившего статистику [4, 112]

которая при довольно большенный выборке распределена нормально, имеет нулевую среднюю и дисперсию, равную единице (Тинтнер, 1965).

Автокорреляционные функции

Последовательность коэффициентов корреляции rk, где k = 1, 2, …, n, как функция интервала k меж наблюдениями именуется автокорреляционной функцией (АКФ).

Вид выборочной автокорреляционной функции тесновато связан со структурой ряда.

· Автокорреляционная функция rk для «белоснежного шума», при k >0, также образует стационарный временной ряд со средним значением 0.

· Для стационарного ряда АКФ стремительно убывает с ростом k. При наличии ясного тренда автокорреляционная функция приобретает соответствующий вид весьма медлительно спадающей кривой [3, 268].

· В случае выраженной сезонности в графике АКФ также находятся выбросы для запаздываний, кратных периоду сезонности, но эти выбросы могут быть завуалированы присутствием тренда либо большенный дисперсией случайной составляющие.

Разглядим примеры автокорреляционной функции:

· на рис. 1 представлен график АКФ, характеризующегося умеренным трендом и непонятно выраженной сезонностью;

· рис. 2 показывает АКФ ряда, характеризующегося феноменальной сезонной детерминантой;

· фактически незатухающий график АКФ ряда (рис. 3) свидетельствует о наличии ясного тренда.

В общем случае можно полагать, что в рядах, состоящих из отклонений от тренда, автокорреляции нет. К примеру, на рис. 4 представлен график АКФ для остатков, приобретенных от выравнивания ряда, весьма напоминающий процесс «белоснежного шума». Но нередки случаи, когда остатки (случайная компонента h ) могут оказаться автокоррелированными, к примеру, по последующим причинам [1, 172]:

· в детерминированных либо стохастических моделях динамики не учтен значимый фактор[3]

· в модели не учтено несколько несущественных причин, обоюдное воздействие которых оказывается значимым вследствие совпадения фаз и направлений их конфигурации;

· избран неверный тип модели (нарушен принцип контринтуитивности);

· случайная компонента имеет специфическую структуру.

Аспект Дарбина-Уотсона

Аспект Дарбина-Уотсона (Durbin, 1969) представляет собой всераспространенную статистику, созданную для тестирования наличия автокорреляции остатков первого порядка опосля выравнивания ряда либо в регрессионных моделях.

Численное значение коэффициента равно

Вероятные значения аспекта находятся в интервале от 0 до 4, при этом табулированы его табличные пороговые значения для различных уровней значимости (Лизер, 1971).

Значение d близко к величине 2*(1 — r1), где r — выборочный коэффициент автокорреляции для остатков. Соответственно, безупречное значение статистики — 2 (автокорреляция отсутствует). Наименьшие значения соответствуют положительной автокорреляции остатков, огромные – отрицательной [2, 193].

К примеру, опосля выравнивания ряда ряд остатков имеет аспект d = 1.912. Подобная статистика опосля выравнивания ряда — d = 1.638 — свидетельствует о некой автокоррелированности остатков.

Глава 2. Примеры практических расчетов при помощи макроса Excel «Автокорреляционная функция»

Все данные взяты с веб-сайта http://e3.prime-tass.ru/macro/

Пример 1. ВВП (Валовой внутренний продукт — макроэкономический показатель, отражающий рыночную стоимость всех конечных товаров и услуг, то есть предназначенных для непосредственного употребления, произведённых за год во всех отраслях экономики на территории государства) РФ (Российская Федерация — государство в Восточной Европе и Северной Азии, наша Родина)

Приведем данные о ВВП (Валовой внутренний продукт — макроэкономический показатель, отражающий рыночную стоимость всех конечных товаров и услуг, то есть предназначенных для непосредственного употребления, произведённых за год во всех отраслях экономики на территории государства) РФ (Российская Федерация — государство в Восточной Европе и Северной Азии, наша Родина)

ACF — Что такое ACF?

Advanced Custom Fields плагин для WordPress делает работу с случайными полями легкой и резвой. Произвольные поля интегрированы в WP, но они достаточно неудобны в настройке и не комфортны для юзера. На снимках экрана ниже показана разница меж интегрированы ми случайными полями и Advanced Custom Fields.

Интегрированные произвольные поля Advanced Custom Fields

Группы полей

В Группах полей хранятся произвольные поля, условия отображения и зрительные опции. Каждой группе можно указать где она обязана выводится на базе массы опций. Обычная группа полей смотрится так:

Интегрированные произвольные поля

Снутри группы полей можно создавать отдельные произвольные поля. Например, создаем группу полей «Артисты» и в ней 2 поля «Имя» и «Изображение».

Каждое поле имеет огромное количество характеристик, которые меняют тип(текст, изображение, редактор wysiwyg, списки и т.д.), значение по-умолчанию, зависимости и почти все другое. В платной версии плагина доступны еще более полей, упрощающих Вашу жизнь, повторитель, галерея, гибкое содержание и даже глобальные опции веб-сайта!

Положение

Вы сможете весьма гибко настроить где показывать группу полей. В этом Для вас посодействуют логические конструкции либо/и, дозволяющие указать в которых таксономиях необходимо выводить поля.

Опции отображения

Дозволяет настроить зрительное отображения для группы полей. Также можно скрыть ненадобные элементы интрфейса, чтоб не отвлекать юзера. Например, можно скрыть обычное окно редактирования и поставить туда свое. Это дозволяет «разгрузить» рабочее место и создать наиболее комфортным процесс работы.

Вывод значений ACF в темах

В ACF встроенно огромное количество массивных и нужных функций для работы с данными. Они основаны на интегрированных функциях WP, но наиболее гибкие и комфортные. Благодаря этому код становится компактнее и умнее.

При работе с ACF рекомендуется иметь базисные представления о работе с WordPress темами и базы PHP. Функция the_field(‘hero_text’) выведет значение поля в подходящем месте, а get_field(‘hero_text’) возвратит значение поля в переменную. Прочитайте все доступные функции, чтоб быть во всеоружии и применять по-полной способности ACF!

Заключение

ACF — это плагин позволяющий глубоко настроить произвольные поля под свои нужды. Но, не забываете, что данные необходимо вывести в теме.

ACF — легкий, но мощнейший плагин. Вы сможете сделать формы, глобальные опции для веб-сайта и почти все другое. Попытайтесь! Для вас понравится!

Источник