кодирование информации в эвм с помощью спинов фотонов
ЦП Автоматизированные системы управления и промышленная безопасность
БК Автоматизированные системы управления и кибернетика
3. Кодирование данных в ЭВМ
В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц, поэтому компьютер может обрабатывать только информацию, представленную в цифровой форме.
Для преобразования числовой, текстовой, графической, звуковой информации в цифровую необходимо применить кодирование.
Кодирование – это преобразование данных одного типа через данные другого типа. В ЭВМ применяется система двоичного кодирования, основанная на представлении данных последовательностью двух знаков: 1 и 0, которые называются двоичными цифрами (binary digit – сокращенно bit).
Целые числа кодируются двоичным кодом довольно просто (путем деления числа на два). Для кодирования нечисловой информации используется следующий алгоритм: все возможные значения кодируемой информации нумеруются и эти номера кодируются с помощью двоичного кода.
Кодирование чисел
Есть два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, второй (так называемое представление числа в формате с плавающей точкой) используется для задания некоторого подмножества действительных чисел.
Кодирование целых чисел производиться через их представление в двоичной системе счисления: именно в этом виде они и помещаются в ячейке. Один бит отводиться при этом для представления знака числа (нулем кодируется знак «плюс», единицей – «минус»).
Кодирование координат
Закодировать можно не только числа, но и другую информацию, например, о том, где находится некоторый объект. Величины, определяющие положение объекта в пространстве, называются координатами. В любой системе координат есть начало отсчёта, единица измерения, масштаб, направление отсчёта, или оси координат. Примеры систем координат – декартовы координаты, полярная система координат, шахматы, географические координаты.
Кодирование текста
Для представления текстовой информации используется таблица нумерации символов или таблица кодировки символов, в которой каждому символу соответствует целое число (порядковый номер). Восемь двоичных разрядов могут закодировать 256 различных символов.
Существующий стандарт ASCII (сокращение от American Standard Code for Information Intercange – американский стандартный код для обмена информацией; 8 – разрядная система кодирования) содержит две таблицы кодирования – базовую и расширенную. Первая таблица содержит 128 основных символов, в ней размещены коды символов английского алфавита, а во второй таблице кодирования содержатся 128 расширенных символов.
Так как в этот стандарт не входят символы национальных алфавитов других стран, то в каждой стране 128 кодов расширенных символов заменяются символами национального алфавита. В настоящее время существует множество таблиц кодировки символов, в которых 128 кодов расширенных символов заменены символами национального алфавита.
Так, например, кодировка символов русского языка Widows – 1251 используется для компьютеров, работающих под ОС Windows. Другая кодировка для русского языка – это КОИ – 8, которая также широко используется в компьютерных сетях и российском секторе Интернет.
В настоящее время существует универсальная система UNICODE, основанная на 16 – разрядном кодировании символов. Эта 16 – разрядная система обеспечивает универсальные коды для 65536 различных символов, т.е. в этой таблице могут разместиться символы языков большинства стран мира.
Кодирование графической информации
В видеопамяти находится двоичная информация об изображении, выводимом на экран. Почти все создаваемые, обрабатываемые или просматриваемые с помощью компьютера изображения можно разделить на две большие группы – растровую и векторнуюграфику.
Растровые изображения представляют собой однослойную сетку точек, называемых пикселями (pixel, от англ. picture element). Код пикселя содержит информации о его цвете.
Цветные изображения воспринимаются нами как сумма трёх основных цветов – красного, зелёного и синего. Например, сиреневый = красный + синий; жёлтый = красный + зелёный; оранжевый = красный + зелёный, но в другой пропорции. Поэтому достаточно закодировать цвет тремя числами – яркостью его красной, зелёной и синей составляющих. Этот способ кодирования называется RGB (Red – Green – Blue). Его используют в устройствах, способных излучать свет (мониторы). При рисовании на бумаге действуют другие правила, так как краски сами по себе не испускают свет, а только поглощают некоторые цвета спектра. Если смешать красную и зелёную краски, то получится коричневый, а не жёлтый цвет. Поэтому при печати цветных изображений используют метод CMY (Cyan – Magenta – Yellow) – голубой, сиреневый, жёлтый цвета. При таком кодировании красный = сиреневый + жёлтый; зелёный = голубой + жёлтый.
В противоположность растровой графике векторное изображение многослойно. Каждый элемент такого изображения – линия, прямоугольник, окружность или фрагмент текста – располагается в своем собственном слое, пиксели которого устанавливаются независимо от других слоев. Каждый элемент векторного изображения является объектом, который описывается с помощью специального языка (математических уравнения линий, дуг, окружностей и т.д.) Сложные объекты (ломаные линии, различные геометрические фигуры) представляются в виде совокупности элементарных графических объектов.
Объекты векторного изображения, в отличие от растровой графики, могут изменять свои размеры без потери качества (при увеличении растрового изображения увеличивается зернистость).
Как всякий звук, музыка является не чем иным, как звуковыми колебаниями, зарегистрировав которые достаточно точно, можно этот звук безошибочно воспроизвести. Нужно только непрерывный сигнал, которым является звук, преобразовать в последовательность нулей и единиц. С помощью микрофона звук можно превратить в электрические колебания и измерить их амплитуду через равные промежутки времени (несколько десятков тысяч раз в секунду). Каждое измерение записывается в двоичном коде. Этот процесс называется дискретизацией. Устройство для выполнения дискретизации называется аналогово-цифровым преобразователем (АЦП). Воспроизведение такого звука ведётся при помощи цифро-аналогового преобразователя (ЦАП). Полученный ступенчатый сигнал сглаживается и преобразуется в звук при помощи усилителя и динамика. На качество воспроизведения влияют частота дискретизации и разрешение (размер ячейки, отведённой под запись значения амплитуды). Например, при записи музыки на компакт-диски используются 16-разрядные значения и частота дискретизации 44 032 Гц.
Описанный способ кодирования звуковой информации достаточно универсален, он позволяет представить любой звук и преобразовывать его самыми разными способами. Но бывают случаи, когда выгодней действовать по-иному.
Издавна используется достаточно компактный способ представления музыки – нотная запись. В ней с помощью специальных символов указывается высота и длительность, общий темп исполнения и как сыграть. Фактически, такую запись можно считать алгоритмом для музыканта, записанным на особом формальном языке. В 1983 г. ведущие производители компьютеров и музыкальных синтезаторов разработали стандарт, определивший такую систему кодов. Он получил название MIDI (Musical Instrument Digital Interface). При таком кодировании запись компактна, легко меняется инструмент исполнителя, тональность звучания, одна и та же запись воспроизводится как на синтезаторе, так и на компьютере.
Конечно, такая система кодирования позволяет записать далеко не всякий звук, она годится только для инструментальной музыки. Но есть у нее и преимущества: чрезвычайно компактная запись, естественность для музыканта (практически любой MIDI-редактор позволяет работать с музыкой в виде обычных нот), легкость замены инструментов, изменения темпа и тональности мелодии.
Есть и другие форматы записи музыки. Среди них – формат MP3, позволяющий с очень большим качеством и степенью сжатия кодировать музыку, при этом вместо 18 – 20 музыкальных композиций на стандартном компакт-диске (CDROM) помещается около 200. Одна песня занимает примерно 3,5 Mb, что позволяет пользователям сети Интернет легко обмениваться музыкальными композициями.
Некоторые элементы квантовой информатики
Квантовый характер таких объектов проявляется в том, что они обладают дискретным набором возможных состояний, которые можно «переключать», воздействуя на них электромагнитным излучением. Фактически, они могут выступать в роли своеобразных логических элементов, на основе которых может быть создана вычислительная система. Так появилась новая наука – квантовая информатика, которая пока что делает лишь первые шаги. Но некоторые ее практические приложения, такие как квантовая криптография, позволяющая создать абсолютно защищенный канал передачи данных, могут использоваться уже в самом ближайшем будущем
Создание экспериментальных методов управления отдельными квантовыми системами привело к появлению новой и необычной области науки – квантовой информатики. Отдельные атомы, азотные вакансии, одиночные фотоны могут выступать в роли логических ячеек, но подчиняются особой квантовой логике. Это позволяет создавать невычислимые системы, способные решить невычисляемые с помощью обычных компьютеров задачи. Синтез информатики и квантовой физики рождает новые технологии в передаче и кодировании информации – квантовую криптографию, позволяющую создать абсолютно защищенный канал передачи данных.
Исследование отдельных квантовых систем, ставшее возможным благодаря развитию и совершенствованию тонких экспериментальных методов, является принципиально новым и многообещающим подходом к изучению природы. Эксперименты с отдельными ионами и нейтральными атомами, взаимодействующими с одиночными фотонами, в 2012 г. были отмечены Нобелевской премией по физике.
Квантовый характер таких объектов проявляется в том, что они обладают дискретным набором возможных состояний, которые можно «переключать», воздействуя на них электромагнитным излучением. И, фактически, они могут выступать в роли своеобразных логических элементов, на основе которых может быть создана вычислительная система.
Вычислить невычислимое
Однако есть ряд задач, решить которые с помощью классических компьютеров в разумные сроки невозможно. Это, в первую очередь, все точные (неэмпирические) квантово-механические расчеты атомов и молекул – если в интересующей нас молекуле содержится N электронов, то необходимое для последовательных вычислений время пропорционально некоторому числу в степени N, и уже для нескольких десятков электронов становится больше времени существования Вселенной. Эти трудности обсуждались в 1981 г. Ричардом Фейнманом в лекции «Моделирование физики с использованием компьютеров».
Но еще в 1980 г. в пионерной работе Юрия Манина «Вычислить невычислимое» (Манин, 1980), выдвигалась идея создания «квантовых автоматов» для расчета процесса разворачивания двойной спирали ДНК – предлагалось использовать для моделирования квантово-механических явлений системы, обладающие не классическими, а квантовыми свойствами.
В те времена, когда были опубликованы работы Манина и Фейнмана, возможность использовать в компьютерах квантовые объекты была лишь гипотетической. Но в последнее время благодаря развитию экспериментальных методик появилась технологическая возможность создавать вычислительные системы, использующие квантовые свойства микроскопических объектов. Естественно, это вызывает огромный интерес у научного сообщества.
Вроде бы ноль, но немного единица
Обычные компьютеры производят математические операции над числами, представленными в двоичном виде, то есть в виде последовательностей нулей и единиц. Двоичная система удобна с точки зрения аппаратной реализации – ячейки памяти, в которых записаны числа, должны иметь всего два состояния – есть напряжение или нет напряжения, есть намагниченность или нет намагниченности и т. д. Процесс вычислений в двоичном счислении сводится к последовательности операций над нулями и единицами, а фактически – к изменению по определенным правилам состояний хранящих их ячеек памяти, регистров.
Квантовый компьютер, как и классический, может быть построен на основе двоичной системы исчисления. Некоторые микроскопические объекты, проявляющие квантовые свойства, обладают двумя состояниями, которые могут быть использованы для кодирования нулей и единиц.
Например, это может быть атом, обладающий собственным магнитным моментом – спином. В магнитном поле такой атом может обладать двумя ориентациями спина – в направлении поля и против поля.
Но, если обычная ячейка памяти содержит либо ноль, либо единицу, квантовый объект может находиться в особом состоянии, называемом суперпозицией. В этом случае, если измерять ориентацию спина атома в магнитном поле, можно получить как спин, направленный вверх, так и направленный вниз. И если такой объект использовать как ячейку памяти, то результат считывания с него информации даст с некоторой вероятностью ноль, и с некоторой вероятностью – единицу.
Кроме того, квантовые ячейки памяти, или как их принято называть, кубиты, могут взаимодействовать между собой, и находиться в одном общем, коллективном квантовом состоянии. В этом случае состояние нескольких ячеек можно изменять практически мгновенно, воздействуя лишь на одну из них. Этот коллективный характер поведения взаимодействующих кубитов, или квантового регистра, как раз и позволяет решать те вычислительные задачи, с которыми не может справиться обычный компьютер.
Наиболее важные требования к квантовому компьютеру как физической системе – возможность управления состоянием каждого отдельного кубита, и полная изоляция от внешнего окружения. Кубит – объект атомных размеров, и чтобы он помнил свое состояние достаточно долго, необходимо, что бы он был изолирован от внешних воздействий или, как говорят, его состояние сохраняло когерентность. Или, по крайней мере, время, за которое происходит разрушение квантовых суперпозиций, должно быть большим, хотя бы в 104 раза превышающим время выполнения одной квантовой логической операции.
Для реальных вычислений кубиты должны быть объединены в квантовый регистр. Отдельные кубиты регистра должны быть различимы и управляемы извне. Кубиты должны быть строго двухуровневыми и не переходить самопроизвольно на какой-либо третий уровень. Кроме того, должна существовать возможность масштабировать квантовый регистр, т. е. добавлять, если нужно, новые кубиты. Необходимо управлять взаимодействием кубитов друг с другом. Именно взаимодействие, его вид и характеристики влияет на то, какие логические операции сможет выполнять квантовый регистр.
Конечное состояние регистра также должно измеряться достаточно быстро. Немаловажную роль играет эффективность такого измерения – нужно уметь считать информацию с микроскопического объекта атомных размеров.
Фотонные кубиты
В настоящее время для реализации квантовых вычислений изучаются различные физические системы (Ladd, 2010). Например, в качестве состояний кубита можно использовать направление поляризации фотонов, которое практически не подвержено декогеренции. Логические операции с помощью фотонов можно выполнять, используя пластины из двулучепреломляющих материалов, вращающих поляризацию света. Основная трудность – реализовать взаимодействие отдельных фотонов, что требует оптических сред с очень высокой нелинейностью. Для этого могут быть использованы эффекты электромагнитно-индуцированной прозрачности или взаимодействие атомов с фотонами в микроволновом резонаторе.
В 2001 г. было показано, что квантовые вычисления могут быть реализованы на основе однофотонных источников, а также детекторов и линейных оптических схем с делителями пучка и интерферирующими одиночными фотонами (Knill, 2001).
Для считывания информации с фотонных кубитов могут быть использованы кремниевые однофотонные детекторы, достигающие квантовой эффективности при комнатной температуре в 70 %. Если же применять сверхпроводящие детекторы, их квантовая эффективность может достигать 95 %, но для этого необходимо охлаждение до 100 мК. Быстродействие сверхпроводящих детекторов может быть радикально увеличено путем использования нанопроволок.
Однако, главный недостаток схем квантовых вычислений, основанных на поляризации фотонов, – большая скорость потерь фотонов, сопоставимая со скоростью декогеренции в альтернативных реализациях квантового компьютера.
Для записи квантовой информации можно использовать сверхтонкие состояния нейтральных атомов, время жизни которых составляет секунды. Дальнодействующие взаимодействия между атомами позволяют выполнять двухкубитовые логические операции, а точность измерения конечного состояния кубита близка к 100 %.
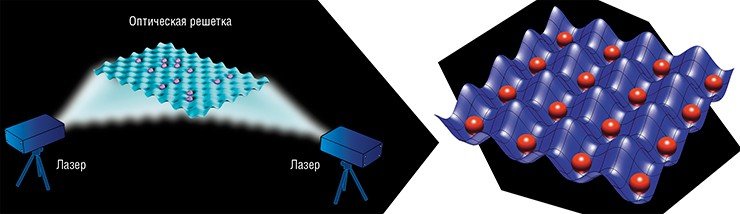
Для создания квантового регистра нейтральные атомы можно захватывать в оптические решетки, образуемые стоячими световыми волнами. Пересечение лучей двух лазеров создает стоячую электромагнитную волну, к пучностям которой притягиваются атомы. Таким образом, из них можно создать пространственно упорядоченные структуры.
В 2010 г. ученым из университета Висконсин-Мэдисон (США) удалось осуществить квантовые логические операции с нейтральными холодными атомами (Isenhower, 2010).
Близкий подход – применение ионов, охлажденных лазерным излучением за счет сил резонансного светового давления и удерживаемых электрическим полем.
Квантовые регистры, составленные из нескольких кубитов, были успешно реализованы в молекулах с использованием ядерного магнитного резонанса (ЯМР). В магнитном поле ядерные спины начинают прецессировать, ориентируясь параллельно или антипараллельно относительно направления магнитного поля. Этим двум возможным направлениям соответствуют логические состояния кубитов. В молекулах частота прецессии для различных атомов будет отличаться. Это позволяет индивидуально адресоваться к отдельным атомам в молекуле, используя резонансное электромагнитное излучение. Простейшие квантовые алгоритмы были продемонстрированы в квантовых ЯМР-компьютерах на основе органических молекул, но масштабирование таких систем пока невозможно.
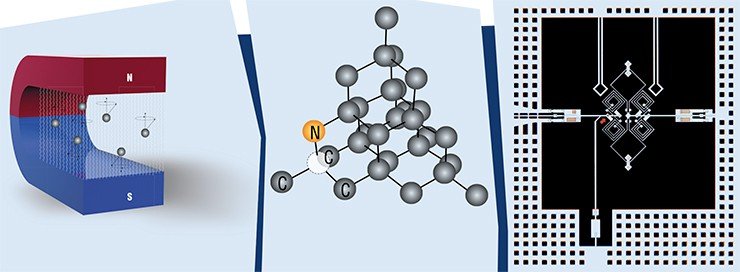
Вместо массивов нейтральных атомов, удерживаемых лазерным излучением, можно использовать массивы «искусственных атомов», например, квантовых точек в полупроводниках (Валиев, 2001). Логические состояния кубита в этом случае представляются двумя состояниями спина электрона в квантовой точке. Также для создания кубитов можно использовать донорные атомы фосфора в полупроводниках или азотные вакансии в алмазах. Спиновые состояния таких кубитов легко управляются внешними электромагнитными полями, время жизни спинового состояния достигает миллисекунд, а спин-спиновые взаимодействия позволяют получить когерентные суперпозиции состояний и реализовать двухкубитовые и более операции.

Широко известным и достаточно перспективным методом реализации квантового компьютера является использование сверхпроводников – в этом случае отдельные кубиты могут иметь мезоскопический характер и содержать до
10 10 движущихся квантово коррелированно электронов. Преимущество такого подхода – большие времена декогеренции.
Многие из этих методов в настоящее время развиваются, в частности, в Институте физики полупроводников СО РАН, включая исследование квантовых точек, азотных вакансий в алмазе и взаимодействия ультрахолодных ридберговских атомов.
Квантовая криптография
Успехи в создании квантовых логических элементов позволяют перейти к практической реализации принципов квантовой информатики. Хотя квантовые вычислительные системы обладают потенциально огромными возможностями, они, конечно же, не заменят обычные компьютеры. Аналогично, появление лазеров не привело к исчезновению обычных источников света – но они создали возможность решения новых и специфических задач.
К примеру, эксперименты в квантовой оптике позволили продемонстрировать такие фундаментальные физические явления, как квантовая запутанность, – измерение состояния одного квантового объекта может привести к тому, что состояние другого объекта, квантово коррелированного с первым, изменится. Излагаемый далее протокол квантовой криптографии не требует квантовой запутанности – в его основе лежит невозможность копирования квантового состояния.
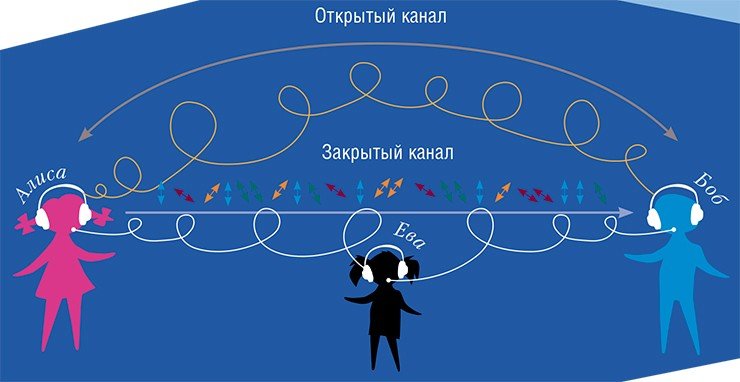
Передатчик (Алиса) кодирует информацию путем задания той или иной поляризации испускаемых им фотонов, скажем, пропуская их через материал, который вращает плоскость поляризации. Вертикальная поляризация означает «1», а горизонтальная – «0». Приемник (Боб) анализирует полученный фотон с помощью устройства, пропускающего только вертикально поляризованные частицы. И, соответственно, получает «1», когда регистрирует сигнал, или «0», когда сигнала нет.
Допустим, что Алиса испускает также и фотоны, поляризованные по диагонали – под углом в 45 и 135° (в другом базисе). Тогда Боб, анализируя диагонально поляризованный фотон вертикально ориентированным анализатором, будет получать не достоверные значения нулей и единица с некоторой вероятностью ошибется: в 50 % случаев он будет получать «1», в 50 % – «0». Чтобы получить достоверную информацию, приемник должен знать, какой тип поляризации использовал передатчик при кодировании. Об этом Алиса сообщает Бобу по отдельному, открытому каналу, используя тот или иной протокол.
Если кто-то будет пытаться прослушать канал обмена данными (перехватчик, или Ева), то он заведомо не будет знать базиса. Чтобы остаться незамеченной, Еве необходимо поглотить фотон и испустить такой же точно квант света обратно в канал. Но она не знает, какой был базис поляризации – вертикальный или диагональный, она получила только лишь сигналы «0» или «1». И, соответственно, не может в точности скопировать такой поглощенный фотон, чем вносит дополнительную ошибку в получаемую Бобом информацию. Благодаря этому Алиса и Боб узнают о том, что канал кто-то прослушивает.
Системы секретной передачи данных на основе методов квантовой криптографии производятся компаниями ID Quantique и MagiQ Technologies. Кроме того, исследования в данной области ведутся в интересах органов безопасности ряда стран. В ИФП СО РАН созданы российские прототипы систем квантовой криптографии.
Манин Ю. И. Вычислимое и невычислимое. М.: Сов. радио, 1980. 128 с.
Isenhower L., Urban E., Zhang X. L., et al. // Phys. Rev. Let., 2010. V. 104.
Feynman R. P. Engineering and Science/ 1960. P. 22–36. http://www.nobelprize.org/nobel_prizes/physics/laureates/2012/.
Feynman R. P. Simulating physics with computers // Int. J. Theor. Phys. 1982. V. 21. P. 467;
Feynman R. P. Quantum mechanical computers // Opt. News. 1985. V. 11. P. 11.
Knill E., Laflamme R., and Milburn G. J. // Nature. 2001. V. 409. P. 46–52.
Ladd T. D., Jelezko F., Laflamme R., et al. // Nature. 2010. V. 464. P. 45.
Nature Physics Insight // Quantum Simulation. 2012. V. 8. No 4. Ed. by A. Trabesinger.
Nielsen M. A., Chuang I. L. Quantum Computation and Quanum Information. Cambridge, UK: Cambridge University Press. 2010.
DiVincenzo D. P. Quantum computation // Science. 1995. V. 270. P. 255;
DiVincenzo D. P. The Physical Implementation of Quantum Computation // Fortschr. Phys. 2000. V. 48. P. 771.