кодирование строки по хаффману python
Русские Блоги
Принцип кодирования Хаффмана (Huffman Coding), этапы работы, реализация на Python
Кодирование ХаффманаЭто типичное применение жадного алгоритма. Кодирование Хаффмана использует частоту (вероятность) каждой части данных для перекодирования этих данных с точки зрения теории информации. Результатом кодирования Хаффмана является получение более короткого кода для данных с более высокой частотой появления и более длинного кода для данных с более низкой частотой появления.
Давайте рассмотрим пример, чтобы проиллюстрировать шаги кодирования Хаффмана: Теперь есть данные [a, a, a, a, a, b, b, b, b, c, c, c, d, d, e]. Видно, что символ a появляется 5 раз, символ 2 появляется 4 раза, символ c появляется 3 раза, символ d появляется 2 раза и символ e появляется 1 раз.
Алгоритм слияния: сначала выберите два леса с наименьшим значением частоты корневого узла и объедините два леса в одно дерево, значение корневого узла которого является суммой двух вышеуказанных значений частоты корневого узла, а два вышеуказанных корневых узла являются новыми. Левый и правый узлы корневого узла дерева. Повторяйте этап объединения, пока не закончится алгоритм объединения всех лесов в одно дерево. Процесс работы алгоритма следующий:
| шаг | положение дел |
|---|---|
| init |  |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
После построения дерева Хаффмана проследуйте по пути обхода, чтобы получить кодировку каждого символа:
Русские Блоги
Поддержите оригинальные функции Nuggets
Вторая глава SICP фокусируется на абстракции данных, которую можно просто понять как структуру данных языка Lisp. Конечно, это понимание может использоваться только как переход, потому что в Лиспе нет разницы между данными и процессом, и нет необходимости в дополнительной концепции для описания процесса абстрагирования данных.2.3.4 Возьмите кодирование Хаффмана в качестве примера, чтобы показать, как реализовать представление и работу структуры данных двоичного дерева Хаффмана в Лиспе. После выполнения упражнений в этом разделе (полное создание, декодирование и кодирование дерева кодирования Хаффмана) в этой статье будет использоваться Лисп. (Здесь используется DrRacket #lang sicp Узор, который примерно Scheme ) Сравнить с версией программы на Python.
1. Дерево Хаффмана
Кодирование Хаффмана основано на взвешенном двоичном дереве, которое выражается в Python:
Лисп представлен списком:
2. Алгоритм Хаффмана.
Чтобы сгенерировать оптимальное двоичное дерево, кодирование Хаффмана принимает частоту появления символа в качестве веса, и каждый раз два узла с наименьшим весом выбираются в качестве левой и правой ветвей сгенерированного двоичного дерева, а сумма весов используется в качестве веса корневого узла. Алгоритм создания двоичного дерева с кратчайшим взвешенным путем снизу вверх.
Согласно этому алгоритму, дерево Хаффмана может быть построено на основе статистической информации «частота символов». В реализации Python необходимо только каждый раз переупорядочивать все узлы в соответствии с их весами:
Lisp обычно использует рекурсивный процесс для выполнения операций цикла. Упорядоченный набор, подобный сортировке вставкой, реализуется следующим образом:
Следующий абзац похож на функцию вывода списка Python, которая может помочь вам лучше почувствовать простоту и красоту Python:
Наконец, сгенерируйте дерево кодирования Хаффмана на основе упорядоченного набора «частота символов»:
3. Кодирование и декодирование
Корневой узел каждого уровня в двоичном дереве Лиспа кэширует символы, которые появляются во всех поддеревьях, а пространство обменивается на время:
Процесс декодирования более простой, просто следуйте «0» Возьмите левое поддерево и встретите «1» Просто возьмите правила правильного поддерева:
Следует отметить, что вышеупомянутый алгоритм не гарантирует, что дерево Хаффмана, генерируемое каждый раз, является уникальным, потому что могут быть проблемы с равными весами и распределением левого и правого поддеревьев, но для одного и того же дерева результаты кодирования и декодирования являются интероперабельными. оф.
4. Резюме
Python обладает удивительной гибкостью, обеспечивая при этом простоту и элегантность. Мы даже можем имитировать Scheme Синтаксис для выполнения всех вышеуказанных процедур:
Хотя делать это бессмысленно, идея абстрагирования описания процесса до уровня функции и последующего управления функцией также очень важна в Python.
Большинство вышеперечисленных кодов выполняется в поездах или автомобилях во время поездки. Есть несколько возможностей испытать «веселье» автономного программирования. sort с участием nonlocal Благодаря резюме при написании PyTips, так что я все еще надеюсь, что успею заполнить 0xFF 。
Сжатие данных алгоритмом Хаффмана
Вступление
В данной статье я расскажу вам о широко известном алгоритме Хаффмана, и вы наконец разберетесь, как все там устроено изнутри. После прочтения вы сможете своими руками(а главное, головой) написать архиватор, сжимающий реальные, черт подери, данные! Кто знает, быть может именно вам светит стать следующим Ричардом Хендриксом!
Да-да, об этом уже была статья на Хабре, но без практической реализации. Здесь же мы сфокусируемся как на теоретической части, так и на программерской. Итак, все под кат!
Немного размышлений
В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASY\n». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — ‘\n’. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или ‘\n’) — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.
Кодирование
Почему бы символу ‘S’ не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ‘ ‘(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:
Ни один код не должен быть префиксом другого
Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:
Символы с наибольшим количеством вхождений должны кодироваться наименьшим возможным количеством битов. Приведу пример одной из возможных таблиц кодов:
Таким образом, закодированное сообщение будет выглядеть так:
Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос: как этот салага придумал код как создать таблицу кодов? Об этом пойдет речь ниже.
Построение дерева Хаффмана
Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:
Это не полный код, полный код будет ниже.
Вот сам алгоритм построения дерева:
Здесь символ «lf»(linefeed) обозначает переход на новую строку, «sp» (space) — это пробел.
А что дальше?
Мы получили дерево Хаффмана. Ну окей. И что с ним делать? Его и за бесплатно не возьмут А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.
Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.
Декодирование
Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:
Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:
Ни один код не должен являться префиксом другого
Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.
Реализация
Пришло время унижать мой код писать архиватор. Назовем его Compressor.
Начнем с начала. Первым делом пишем класс Node:
Класс, создающий дерево Хаффмана:
Класс, содержащий который кодирует/декодирует:
Класс, облегчающий запись в файл:
Класс, облегчающий чтение из файла:
Ну, и главный класс:
Файл с инструкциями readme.txt предстоит вам написать самим 🙂
Заключение
Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу моей некомпетентности улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!
Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то только не по лицу вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.
Выпустил upgrade: добавил GUI + изменил алгоритм обработки исходного текста так, чтобы не читать весь файл в память. Короче, кидаю ссылку на git для любознательных: сами всё увидите.
Благодарности
Как и автор каждой хорошей книги, я созидал эту статью не без помощи других людей. Имхо, очень мало людей сделало что-то крутое в одиночку.
Огромное спасибо Исаеву Виталию Вячеславовичу за небходимую теоретическую поддержку.
Также, часть материала этой статьи взята из книги Роберта Лафоре «Data Structures and Algorithms in Java». Если сомневаетесь как или окуда начать свой путь в теории алгоритмов и структур данных — берите, не прогадаете.
Алгоритм Хаффмана на пальцах
Вы вероятно слышали о Дэвиде Хаффмане и его популярном алгоритме сжатия. Если нет, то поищите информацию в интернете — в этой статье я не буду вас грузить историей или математикой. Сегодня я хочу просто попытаться показать вам практический пример применения алгоритма к символьной строке.
Примечание переводчика: под символом автор подразумевает некий повторяющийся элемент исходной строки — это может быть как печатный знак (character), так и любая битовая последовательность. Под кодом подразумевается не ASCII или UTF-8 код символа, а кодирующая последовательность битов.
К статье прикреплён исходный код, который наглядно демонстрирует, как работает алгоритм Хаффмана — он предназначен для людей, которые плохо понимают математику процесса. В будущем (я надеюсь) я напишу статью, в которой мы поговорим о применении алгоритма к любым файлам для их сжатия (то есть, сделаем простой архиватор типа WinRAR или WinZIP).
Идея, положенная в основу кодировании Хаффмана, основана на частоте появления символа в последовательности. Символ, который встречается в последовательности чаще всего, получает новый очень маленький код, а символ, который встречается реже всего, получает, наоборот, очень длинный код. Это нужно, так как мы хотим, чтобы, когда мы обработали весь ввод, самые частотные символы заняли меньше всего места (и меньше, чем они занимали в оригинале), а самые редкие — побольше (но так как они редкие, это не имеет значения). Для нашей программы я решил, что символ будет иметь длину 8 бит, то есть, будет соответствовать печатному знаку.
Мы могли бы с той же простотой взять символ длиной в 16 бит (то есть, состоящий из двух печатных знаков), равно как и 10 бит, 20 и так далее. Размер символа выбирается, исходя из строки ввода, которую мы ожидаем встретить. Например, если бы я собрался кодировать сырые видеофайлы, я бы приравнял размер символа к размеру пикселя. Помните, что при уменьшении или увеличении размера символа меняется и размер кода для каждого символа, потому что чем больше размер, тем больше символов можно закодировать этим размером кода. Комбинаций нулей и единичек, подходящих для восьми бит, меньше, чем для шестнадцати. Поэтому вы должны подобрать размер символа, исходя из того по какому принципу данные повторяются в вашей последовательности.
Для этого алгоритма вам потребуется минимальное понимание устройства бинарного дерева и очереди с приоритетами. В исходном коде я использовал код очереди с приоритетами из моей предыдущей статьи.
Предположим, у нас есть строка «beep boop beer!», для которой, в её текущем виде, на каждый знак тратится по одному байту. Это означает, что вся строка целиком занимает 15*8 = 120 бит памяти. После кодирования строка займёт 40 бит (на практике, в нашей программе мы выведем на консоль последовательность из 40 нулей и единиц, представляющих собой биты кодированного текста. Чтобы получить из них настоящую строку размером 40 бит, нужно применять битовую арифметику, поэтому мы сегодня не будем этого делать).
Чтобы лучше понять пример, мы для начала сделаем всё вручную. Строка «beep boop beer!» для этого очень хорошо подойдёт. Чтобы получить код для каждого символа на основе его частотности, нам надо построить бинарное дерево, такое, что каждый лист этого дерева будет содержать символ (печатный знак из строки). Дерево будет строиться от листьев к корню, в том смысле, что символы с меньшей частотой будут дальше от корня, чем символы с большей. Скоро вы увидите, для чего это нужно.
Чтобы построить дерево, мы воспользуемся слегка модифицированной очередью с приоритетами — первыми из неё будут извлекаться элементы с наименьшим приоритетом, а не наибольшим. Это нужно, чтобы строить дерево от листьев к корню.
Для начала посчитаем частоты всех символов:
| Символ | Частота |
|---|---|
| ‘b’ | 3 |
| ‘e’ | 4 |
| ‘p’ | 2 |
| ‘ ‘ | 2 |
| ‘o’ | 2 |
| ‘r’ | 1 |
| ‘!’ | 1 |
После вычисления частот мы создадим узлы бинарного дерева для каждого знака и добавим их в очередь, используя частоту в качестве приоритета:
Теперь мы достаём два первых элемента из очереди и связываем их, создавая новый узел дерева, в котором они оба будут потомками, а приоритет нового узла будет равен сумме их приоритетов. После этого мы добавим получившийся новый узел обратно в очередь. 
Повторим те же шаги и получим последовательно: 


Ну и после того, как мы свяжем два последних элемента, получится итоговое дерево:
Теперь, чтобы получить код для каждого символа, надо просто пройтись по дереву, и для каждого перехода добавлять 0, если мы идём влево, и 1 — если направо:
Если мы так сделаем, то получим следующие коды для символов:
| Символ | Код |
|---|---|
| ‘b’ | 00 |
| ‘e’ | 11 |
| ‘p’ | 101 |
| ‘ ‘ | 011 |
| ‘o’ | 010 |
| ‘r’ | 1000 |
| ‘!’ | 1001 |
Чтобы расшифровать закодированную строку, нам надо, соответственно, просто идти по дереву, сворачивая в соответствующую каждому биту сторону до тех пор, пока мы не достигнем листа. Например, если есть строка «101 11 101 11» и наше дерево, то мы получим строку «pepe».
Важно иметь в виду, что каждый код не является префиксом для кода другого символа. В нашем примере, если 00 — это код для ‘b’, то 000 не может оказаться чьим-либо кодом, потому что иначе мы получим конфликт. Мы никогда не достигли бы этого символа в дереве, так как останавливались бы ещё на ‘b’.
На практике, при реализации данного алгоритма сразу после построения дерева строится таблица Хаффмана. Данная таблица — это по сути связный список или массив, который содержит каждый символ и его код, потому что это делает кодирование более эффективным. Довольно затратно каждый раз искать символ и одновременно вычислять его код, так как мы не знаем, где он находится, и придётся обходить всё дерево целиком. Как правило, для кодирования используется таблица Хаффмана, а для декодирования — дерево Хаффмана.
Входная строка: «beep boop beer!»
Входная строка в бинарном виде: «0110 0010 0110 0101 0110 0101 0111 0000 0010 0000 0110 0010 0110 1111 0110 1111 0111 0000 0010 0000 0110 0010 0110 0101 0110 0101 0111 0010 0010 000»
Закодированная строка: «0011 1110 1011 0001 0010 1010 1100 1111 1000 1001»
Как вы можете заметить, между ASCII-версией строки и закодированной версией существует большая разница.
Приложенный исходный код работает по тому же принципу, что и описан выше. В коде можно найти больше деталей и комментариев.
Все исходники были откомпилированы и проверены с использованием стандарта C99. Удачного программирования!
Чтобы прояснить ситуацию: данная статья только иллюстрирует работу алгоритма. Чтобы использовать это в реальной жизни, вам надо будет поместить созданное вами дерево Хаффмана в закодированную строку, а получатель должен будет знать, как его интерпретировать, чтобы раскодировать сообщение. Хорошим способом сделать это, является проход по дереву в любом порядке, который вам нравится (я предпочитаю обход в глубину) и конкатенировать 0 для каждого узла и 1 для листа с битами, представляющими оригинальный символ (в нашем случае, 8 бит, представляющие ASCII-код знака). Идеальным было бы добавить это представление в самое начало закодированной строки. Как только получатель построит дерево, он будет знать, как декодировать сообщение, чтобы прочесть оригинал.
Python алгоритмы
суббота, 18 июня 2011 г.
Деревья кодирования по Хаффману
С таким кодом, сообщение
BACADAEAFABBAAAGAH
кодируется как строка из 54 бит
001000010000011000100000101000001001000000000110000111
Такие коды, как ASCII и наш код от A до H, известны под названием кодов с фиксированной длиной, поскольку каждый символ сообщения они представляют с помощью одного и того же числа битов. Иногда полезно использовать и коды с переменной длиной (variable-length), в которых различные символы могут представляться различным числом битов. Например, азбука Морзе не для всех букв алфавита использует одинаковое число точек и тире. В частности, E, наиболее частая (в английском) буква, представляется с помощью одной точки. В общем случае, если наши сообщения таковы, что некоторые символы встречаются очень часто, а некоторые очень редко, то мы можем кодировать свои данные более эффективно (т. е. с помощью меньшего числа битов на сообщение), если более частым символам мы назначим более короткие коды. Рассмотрим следующий код для букв с A по H:
С таким кодом то же самое сообщение преобразуется в строку
100010100101101100011010100100000111001111
В этой строке 42 бита, так что она экономит более 20% места по сравнению с приведенным выше кодом с фиксированной длиной.
Одна из сложностей при работе с кодом с переменной длиной состоит в том, чтобы узнать, когда при чтении последовательности единиц и нулей достигнут конец символа. В азбуке Морзе эта проблема решается при помощи специального кода-разделителя (separator code) (в данном случае паузы) после последовательности точек и тире для каждой буквы. Другое решение состоит в том, чтобы построить систему кодирования так, чтобы никакой полный код символа не совпадал с началом (или префиксом) кода никакого другого символа. Такой код называется префиксным (prefix). В вышеприведенном примере A кодируется 0, а B 100, так что никакой другой символ не может иметь код, который начинается на 0 или 100.
В общем случае можно добиться существенной экономии, если использовать коды с переменной длиной, использующие относительные частоты символов в подлежащих кодированию сообщениях. Одна из схем такого кодирования называется кодированием
по Хаффману, в честь своего изобретателя, Дэвида Хаффмана. Код Хаффмана может быть представлен как бинарное дерево, на листьях которого лежат кодируемые символы.
В каждом нетерминальном узле находится множество символов с тех листьев, которые лежат под данным узлом. Кроме того, каждому символу на листе дерева присваивается вес (представляющий собой относительную частоту), а каждый нетерминальный узел имеет вес, который равняется сумме весов листьев, лежащих под данным узлом. Веса не используются в процессе кодирования и декодирования. Ниже мы увидим, как они оказываются полезными при построении дерева.
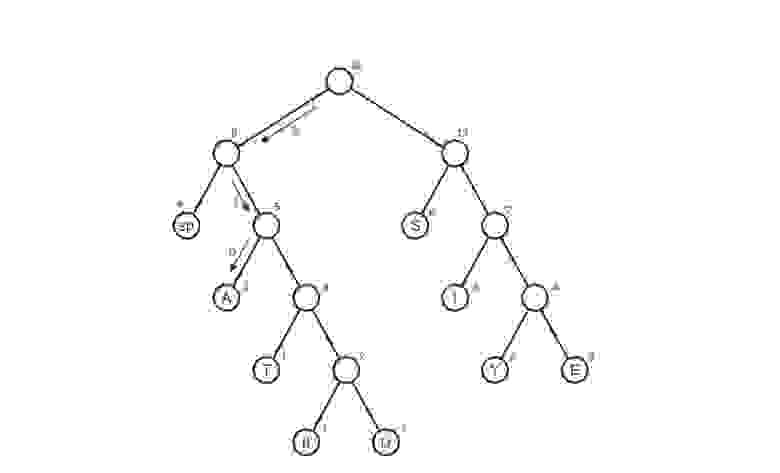
Рисунок ниже изображает дерево Хаффмана для кода от A до H, показанного выше. Веса в вершинах дерева указывают, что дерево строилось для сообщений, где A встречается с относительной частотой 8, B с относительной частотой 3, а все остальные буквы с относительной частотой 1.
Имея дерево Хаффмана, можно найти код любого символа, если начать с корня и двигаться вниз до тех пор, пока не будет достигнута концевая вершина, содержащая этот символ. Каждый раз, как мы спускаемся по левой ветви, мы добавляем 0 к коду, а спускаясь по правой ветви, добавляем 1. (Мы решаем, по какой ветке двигаться, проверяя, не является ли одна из веток концевой вершиной, а также содержит ли множество при вершине символ, который мы ищем.) Например, начиная с корня на рисунке выше, мы попадаем в концевую вершину D, сворачивая на правую дорогу, затем на левую, затем на правую, затем, наконец, снова на правую ветвь; следовательно, код для D — 1011.
Чтобы раскодировать последовательность битов при помощи дерева Хаффмана, мы начинаем с корня и просматриваем один за другим биты в последовательности, чтобы решить, нужно ли нам спускаться по левой или по правой ветви. Каждый раз, как мы добираемся до листовой вершины, мы порождаем новый символ сообщения и возвращаемся к вершине дерева, чтобы найти следующий символ. Например, пусть нам дано дерево, изображенное на рисунке, и последовательность 10001010. Начиная от корня, мы идем по правой ветви (поскольку первый бит в строке 1), затем по левой (поскольку второй бит 0), затем опять по левой (поскольку и третий бит 0). Здесь мы попадаем в лист, соответствующий B, так что первый символ декодируемого сообщения — B. Мы снова начинаем от корня и идем налево, поскольку следующий бит строки 0. Тут мы попадаем в лист, изображающий символ A. Мы опять начинаем от корня с остатком строки 1010, двигаемся направо, налево, направо, налево и приходим в C. Таким образом, всесообщение было BAC.
Порождение деревьев Хаффмана
Если нам дан «алфавит» символов и их относительные частоты, как мы можем породить «наилучший» код? (Другими словами, какое дерево будет кодировать сообщения при помощи наименьшего количества битов?) Хаффман дал алгоритм для решения этой задачи и показал, что получаемый этим алгоритмом код — действительно наилучший код с переменной длиной для сообщений, где относительная частота символов соответствует частотам, для которых код строился. Здесь мы не будем доказывать оптимальностькодов Хаффмана, но покажем, как эти коды строятся
Алгоритм порождения дерева Хаффмана весьма прост. Идея состоит в том, чтобы упорядочить дерево так, чтобы символы с наименьшей частотой оказались дальше всего от корня. Начнем с множества терминальных вершин, содержащих символы и их частоты, как указано в исходных данных, из которых нам надо построить дерево. Теперь найдем два листа с наименьшими весами и сольем их, получая вершину, у которой предыдущие две являются левым и правым потомками. Вес новой вершины равен сумме весов ее ветвей. Исключим два листа из исходного множества и заменим их новой вершиной. Продолжим этот процесс. На каждом шаге будем сливать две вершины с самыми низкими весами, исключая их из множества и заменяя вершиной, для которой они являются левой и правой ветвями. Этот процесс заканчивается, когда остается только одна вершина, которая и является корнем всего дерева. Вот как было порождено дерево Хаффмана на рисунке выше:
Алгоритм не всегда приводит к построению единственно возможного дерева, поскольку на каждом шаге выбор вершин с наименьшим весом может быть не единственным. Выбор порядка, в котором будут сливаться две вершины (то есть, какая из них будет левым, а какая правым поддеревом) также произволен.
Представление деревьев Хаффмана
В следующих упражнениях мы будем работать с системой, которая использует деревья Хаффмана для кодирования и декодирования сообщений и порождает деревья Хаффмана в соответствии с вышеописанным алгоритмом. Начнем мы с обсуждения того, как представляются деревья.
Листья дерева представляются в виде списка, состоящего из символа leaf (лист), символа, содержащегося в листе, и веса:
Дерево в общем случае будет списком из левой ветви, правой ветви, множества символов и веса. Множество символов будет просто их списком, а не каким-то более сложным представлением. Когда мы порождаем дерево слиянием двух вершин, мы получаем вес дерева как сумму весов этих вершин, а множество символов как объединение множеств их символов. Поскольку наши множества представлены в виде списка, мы можем породить объединение при помощи процедуры append, определенной нами ранее.
Если мы порождаем дерево таким образом, то у нас будут следующие селекторы:
Процедуры symbols и weight должны вести себя несколько по-разному в зависимости от того, вызваны они для листа или для дерева общего вида. Это простые примеры обобщенных процедур (generic procedures) (процедур, которые способны работать более, чем с одним типом данных).
Итак, ради интереса можете посмотреть на результат создания дерева tree=make_code_tree((‘leaf’, (‘A’, None), 8), ((‘leaf’, (‘B’, None), 3), (‘leaf’, (‘E’, None), 1), (‘B’, ‘E’), 4))
Процедура декодирования
Следующая процедура реализует алгоритм декодирования. В качестве аргументов она
принимает список из единиц и нулей, а также дерево Хаффмана.
Пример использования: decode((1, (0,(0, None))),tree), где tree мы создали с вами процедурой make_code_tree выше.
Процедура decode1 принимает два аргумента: список остающихся битов и текущую позицию в дереве. Она двигается «вниз» по дереву, выбирая левую или правую ветвь в зависимости от того, ноль или единица следующий бит в списке (этот выбор делается в процедуре choose_branch). Когда она достигает листа, она возвращает символ из него как очередной символ сообщения, присоединяя его посредством cons к результату декодирования остатка сообщения, начиная от корня дерева. Обратите внимание на проверку ошибок в конце choose_branch, которая заставляет программу протестовать, если во входных данных обнаруживается что-либо помимо единиц и нулей.
Множества взвешенных элементов
В нашем представлении деревьев каждая нетерминальная вершина содержит множество символов, которое мы представили как простой список. Однако алгоритм порождения дерева, который мы обсуждали выше, требует, чтобы мы работали еще и с множествами листьев и деревьев, последовательно сливая два наименьших элемента. Поскольку нам нужно будет раз за разом находить наименьший элемент множества, удобно для такого множества использовать упорядоченное представление.
Мы представим множество листьев и деревьев как список элементов, упорядоченный
по весу в возрастающем порядке. Следующая процедура adjoinset для построения множеств работает так, что элементы сравниваются по своим весам, и никогда не бывает так, что добавляемый элемент уже содержится в множестве.
Следующая процедура принимает список пар вида символ–частота, например ((A4) (B 2) (C 1) (D 1)), и порождает исходное упорядоченное множество листьев,готовое к слиянию по алгоритму Хаффмана:
Пример использования: make_leaf_set((((‘A’, None), 4), (((‘B’, None), 2), (((‘C’, None), 1), (((‘D’, None), 1), None)))))
Ну вот и все, тут конечно еще есть над чем поработать, но идея я надеюсь вам ясна.
И практики хватило X)))