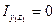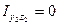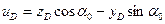Момент сопротивления что это простым языком

Момент инерции и момент сопротивления

При определении сечения строительных конструкций очень часто необходимо знать момент инерции и момент сопротивления для рассматриваемого поперечного сечения конструкции. Что такое момент сопротивления и как он связан с моментом инерции изложено отдельно. Кроме того, для сжимаемых конструкций также нужно знать значение радиуса инерции. Определить момент сопротивления и момент инерции, а иногда и радиус инерции для большинства поперечных сечений простой геометрической формы можно по давно известным формулам:

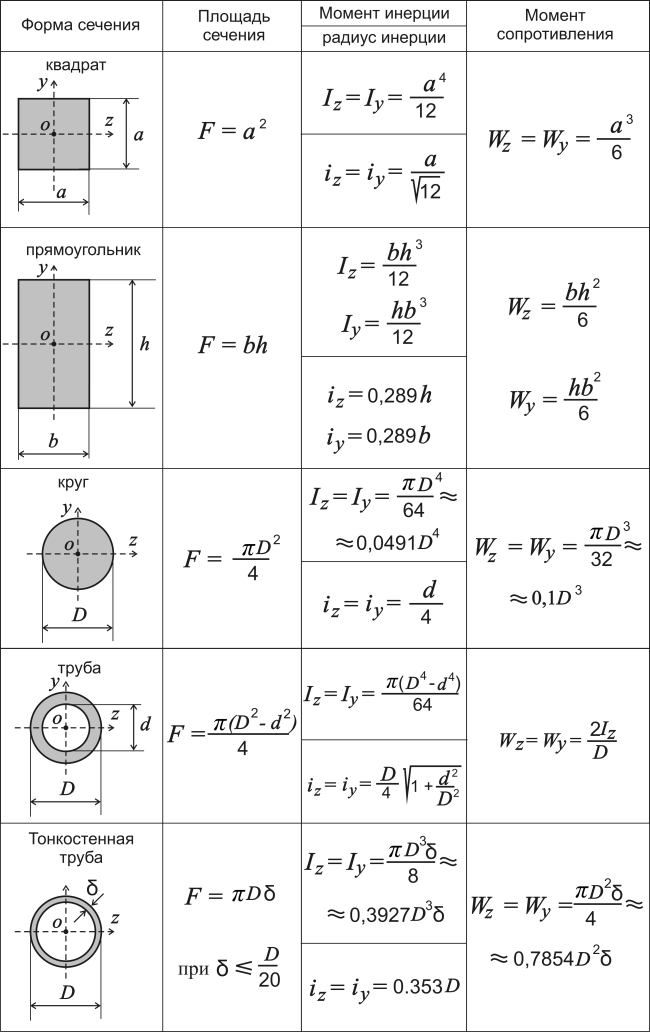
Таблица 1. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм.

Обычно, этих формул достаточно для большинства расчетов, но случаи бывают всякие и сечение конструкции может быть не такой простой геометрической формы или положение осей, относительно которых нужно определить момент инерции или момент сопротивления, может быть не таким, тогда можно воспользоваться следующими формулами:

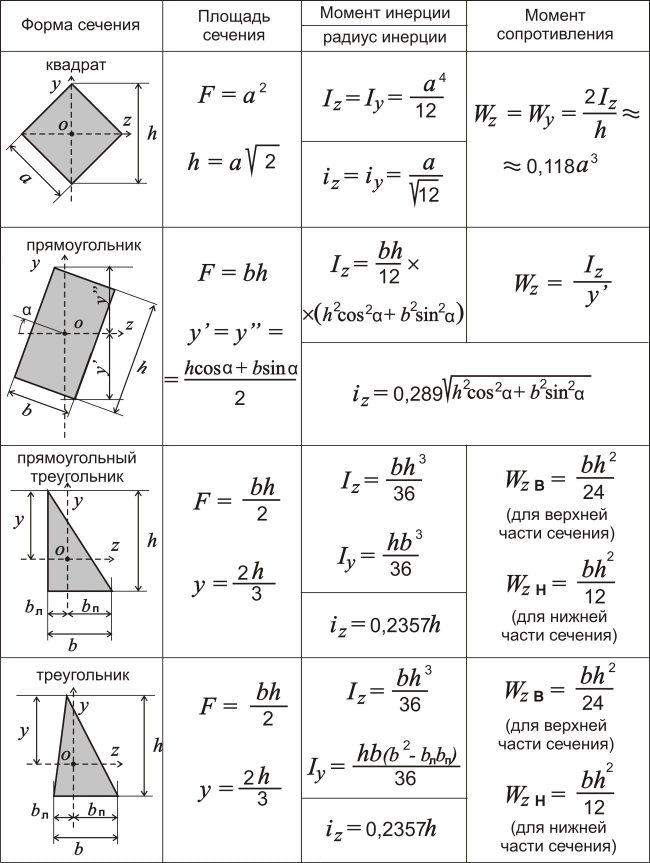
Таблица 2. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций более сложных геометрических форм

Как видно из таблицы 2, высчитывать момент инерции и момент сопротивления для неравнополочных уголков достаточно сложно, да нет в этом необходимости. Для неравнополочных и равнополочных прокатных уголков, а также для швеллеров, двутавров и профильных труб есть сортаменты. В сортаментах значения момента инерции и момента сопротивления приводятся для каждого профиля.

Таблица 3. Изменения моментов инерции и моментов сопротивления в зависимости от положения осей.

Формулы из таблицы 3 могут понадобиться для расчета наклонных элементов кровли.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Было бы неплохо объяснить на наглядном примере для особо одаренных, типа меня, что такое момент инерции и с чем его едят. На специализированных сайтах как-то всё очень запутанно, а у Дока есть явный талант довести информацию, быть может не самую сложную, но очень грамотно и понятно

В принципе все предельно ясно, но здесь проще www.kataltim.ru

требуется определить момент инерции для сложного нестандартного сечения. сечение: прямоугольник с двумя пазами. внешне похоже на букву «Ш». не получается найти какую либо информацию. буду признателен за какую нибудь информацию

Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона» (http://doctorlom.com/item249.html)
там в частности определяется момент инерции тоже не совсем простого сечения.

Вот здесь http://otvet.mail.ru/question/33111076
дана другая формула для момента сопротивления трубы, а именно: W=(D^3-d^3)*3,14/32.
Объясните, пожалуйста, правильность этой формулы (или неправильность).

Формула из приведенного вами источника неправильная (ею можно пользоваться только для приблизительных вычислений) и проверить это легко.
Чтобы определить момент инерции сечения трубы, достаточно вычесть из момента инерции стержня круглого сечения (тут при вычислениях используется наружный диаметр трубы) момент инерции отверстия (внутренний диаметр, ведь внутри трубы никакого материала нет, на то она и труба). После простейших математических преобразований мы получим формулу момента инерции трубы, приведенную в таблице.
А для того, чтобы определить момент сопротивления, нужно момент инерции разделить на максимальное расстояние от центра тяжести до самой дальней точки сечения, соответственно на D/2, или умножить на 2/D.
В итоге получить указанную вами формулу невозможно и чем толще будет стенка трубы, тем больше будет погрешность при использовании этой формулы.

Не смог найти инфо о том в каких единицах (мм, см, м) все значения в формулах.
Попробовал посчитать Wz для уголка 210х90мм (если у швел.24П срезать верхнюю полку), получилось 667,5 см3, при условии что все значения в см.
Для примера, у швел.24П (до срезания полки) Wx(Wz)=243 см3.

Это общие формулы. В каких единицах подставите значения, в таких и получите результат, только само собой уже в кубических. Но если начали подставлять, например, в сантиметрах, то так и нужно продолжать.
У швеллера без полки момент сопротивления по умолчанию не может быть больше чем у целого швеллера. Для приблизительного определения момента сопротивления швеллера без полки вы можете воспользоваться формулами для неравнополочного уголка (только для определения Wz, для Wy эти формулы не подойдут).

Если сечение трубы ослаблено несколькими значительными отверстиями, как учесть это при расчёте момента инерции и момента сопротивления? Труба 32.39см и в ней 9 отв. диам.2.8см в сечении(шаг отвермтий 10см. по длине трубы).

Неравноплечий уголок.При вычислении Wy не y,а H-y

Не пойму, о чем вы. Определение момента сопротивления относительно оси у в таблицах вообще не приводится.

Для треугольников при вычислении Wzп h в квадрате.

Все верно. Теперь понял, о чем вы. Более корректно было бы указать момент сопротивления для верхней и для нижней части сечения, а я указал только для нижней. Ну а при определении момента сопротивления треугольников банально пропущен квадрат.
Исправил. Спасибо за внимательность.

Здравствуете! Кто может помочь о правильности расчета http://ej.kubagro.ru/2011/02/pdf/19.pdf
я не могу понят откуда значение берется момент сопротивления. Помогите пожалуйста!

Что именно вам не понятно (вычитывать весь документ у меня нет времени). Если речь о балке, лежащей на упругом основании, то скорее всего балка эта имеет прямоугольное сечение (см. таблицу 1).

Если максимально упростить, то:
Сначала определяете момент инерции отверстия (для упрощения расчетов его можно принимать прямоугольным). Затем из момента инерции швеллера вычитаете момент инерции отверстия, затем делите полученный момент инерции на половину высоты швеллера и получаете момент сопротивления.

здравствуйте,Сергей. я прочитал некоторые ваши статьи,очень интересно и понятно(в основном).я хотел бы рассчитать балку двутаврового сечения,но не могу найти Ix и Wx. дело в том что она не стандартная,я её буду делать сам,из дерева.можете ли вы мне помочь? я оплачу.только я не смогу оплатить электронными средствами т.к. не знаю как этим пользоваться.

Игорь, я отправил вам письмо.

Уважаемый доктор, желаю вам всего найлучшего. Помогите пожалуйста, какими формулами нужны для подбора и проверки на прочность балку следующих сечений,:Швеллер,уголок и бульбовый профиль, имея допускаемый момент сопротивления W=58,58cm3. спасибо большое и жду вашу помощь.

Посмотрите статью «Расчет стальных однопролетных балок с шарнирными опорами при изгибе согласно СП 16.13330.2011», там все достаточно подробно расписано.

Здравствуйте пожалуйста подскажите почему Ql^2/8 почему деленная на 8 и почему иногда делим на 6 и 24 итд подскажите пожалуйста только это не понял

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

МОМЕНТ СОПРОТИВЛЕНИЯ

геом. хар-ка поперечного сечения стержня (балки, вала), определяющая его сопротивляемость в рассматриваемом сечении изгибу или кручению и равная осевому (или полярному) моменту инерции, делённому на расстояние от оси (или центра тяжести) до наиболее удалённой точки сечения. М. с. применяют в ф-лах сопротивления материалов и строит. механики.

Смотреть что такое «МОМЕНТ СОПРОТИВЛЕНИЯ» в других словарях:

Момент сопротивления — – отношение момента инерции относительно определенной оси сечения к расстоянию от центра тяжести сечения до точки на линии, перпендикулярной оси (проходящей через центр тяжести), максимально удаленной от центра тяжести сечения. [Полякова, Т … Энциклопедия терминов, определений и пояснений строительных материалов

момент сопротивления — atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Konstrukcijos elemento skerspjūvio geometrinė charakteristika, rodanti elemento atsparumą lenkimui arba sukimui. atitikmenys: angl. moment of resistance vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

момент сопротивления — atsparumo momentas statusas T sritis fizika atitikmenys: angl. moment of resistance vok. Widerstandsmoment, n rus. момент сопротивления, m pranc. moment résistant, m … Fizikos terminų žodynas

МОМЕНТ СОПРОТИВЛЕНИЯ — геометрическая характеристика поперечного сечения стержня, показывающая сопротивляемость стержня в рассматриваемом сечении изгибу или кручению (Болгарский язык; Български) съпротивителен момент (Чешский язык; Čeština) průřezový modul; modul… … Строительный словарь

МОМЕНТ СОПРОТИВЛЕНИЯ ПЛАСТИЧЕСКИЙ — момент сопротивления в поперечном сечении изгибаемого стержня, определяемый из условия образования в сечении пластического шарнира (Болгарский язык; Български) пластичен съпротивителен момент (Чешский язык; Čeština) plastický průřezový modul… … Строительный словарь

момент сопротивления (тормозной) вращающегося электродвигателя — 3.9 момент сопротивления (тормозной) вращающегося электродвигателя : Вращающий момент на валу электродвигателя, действующий так, чтобы снизить частоту вращения двигателя. Источник: СТО 70238424.29.160.30.002 2009: Электродвигатели. Организация… … Словарь-справочник терминов нормативно-технической документации

момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus antrajam ploto momentui, padalytam iš atstumo nuo ašies iki toliausiai nuo jos esančio ploto taško. atitikmenys: angl. section modulus vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

момент сопротивления сечения — ašinis ploto atsparumo momentas statusas T sritis fizika atitikmenys: angl. section modulus vok. Widerstandsmoment gegen Biegung, n rus. момент сопротивления сечения, m pranc. module résistant, m … Fizikos terminų žodynas

Момент сопротивления качению колеса — 72. Момент сопротивления качению колеса Mf Источник: ГОСТ 17697 72: Автомобили. Качение колеса. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

момент сопротивления сечения — [section modulus] геометрическая характеристика поперечного сечения тела, равная отношению момента инерции к расстоянию от оси наиболее удаленной точки сечения. Смотри также: Момент момент прокатки момент количества движения момент инерции … Энциклопедический словарь по металлургии

Источник

Основы сопромата, момент сопротивления

10. Определение момента сопротивления.

Для абсолютного большинства строительных материалов значение расчетного сопротивления уже определено эмпирическим путем, поэтому определить параметры сечения, на которое действуют растягивающие или сжимающие напряжения, не сложно. Значения расчетных сопротивлений для большинства строительных материалов есть в разного рода справочниках, тем не менее при большом желании эти значения можно определить и самому.

Рисунок 10.1. Внутренние напряжения в поперечном сечении балки.

В этом случае, если нам известна нагрузка и расчетное сопротивление материала, то можно легко определить площадь сечения конструкции:

S ≥ Q / R (10.1)

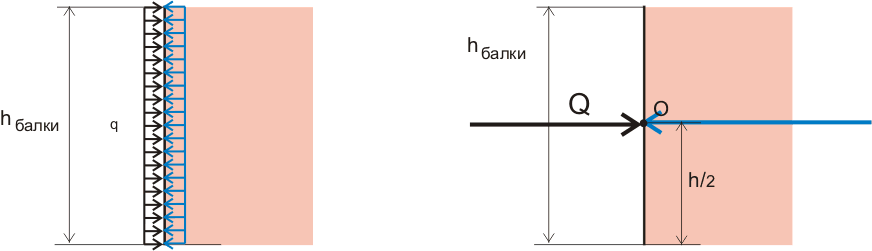
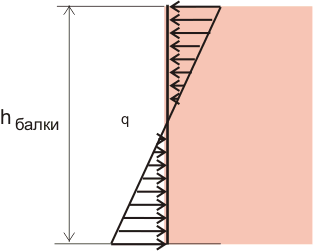
Пример №2. На поперечное сечение балки действует изгибающий момент, который можно заменить парой сил (рисунок 8.2) или распределенной нагрузкой, изменяющейся по высоте (рисунок 8.3). Т.е. растягивающие и сжимающие нормальные напряжения изменяются по высоте балки и поэтому использовать приведенную выше формулу нельзя, нужно как-то учитывать изменение внутренних напряжений в зависимости от высоты балки.

Рисунок 8.2. Увеличение значения сил при уменьшении высоты балки при одинаковом вращающем моменте.

Рисунок 8.3. Изменение распределенной нагрузки по высоте балки.

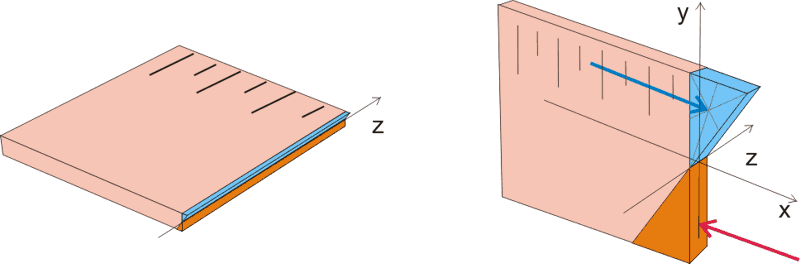
Для наглядности на пару минут вернемся к нашей линейке. Если мы возьмем линейку, которая лежала на книгах плашмя, поставим ее и приложим к линейке точно такую же нагрузку как и к лежащей плашмя линейке, то линейка вообще не прогнется, точнее прогнется, но увидеть это невооруженным глазом невозможно. В чем же дело? ведь ни нагрузка, ни длина балки и, соответственно, изгибающий момент, ни материал балки, ни сечение балки не изменились, изменилось только положение балки в пространстве. Теория сопротивления материалов объясняет это чудо так: при действии на балку нагрузки балка деформируется (прогибается), при этом верхняя часть балки сжимается и в этой части возникают сжимающие напряжения, а нижняя часть балки растягивается и в этой части возникают растягивающие напряжения. Эти напряжения называются нормальными, так как они направлены перпендикулярно поперечному сечению балки (по нормали).

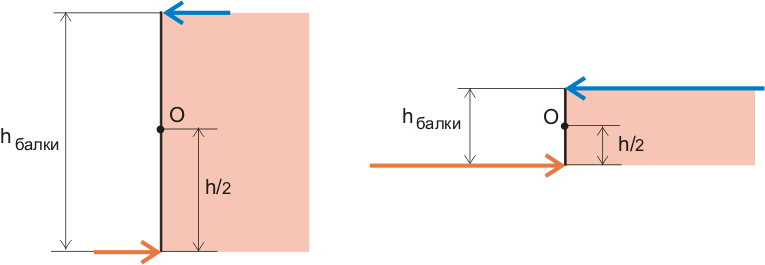
Конечно же при деформации балки в любом поперечном сечении возникают и касательные напряжения, направленные параллельно поперечному сечению (значение этих напряжений можно определить по эпюре «Q», рисунки 7.1 и 7.2), однако значение касательных напряжений при простом загружении в сечении, где действует максимальный изгибающий момент, равно нулю. При этом предполагается, что в некоторой точке (а точнее в ряде точек, которые находятся на оси z) поперечного сечения балки никаких деформаций нет, т.е. значение нормальных сжимающих или растягивающих напряжений равно 0, при этом максимальные сжимающие напряжения возникают в самом верхнем слое балки, а максимальные растягивающие напряжения возникают в самом нижнем слое балки. Графически это выглядит так:

Рисунок 10.2. Напряжения, возникающие в поперечном сечении балки при действии изгибающего момента.

Так как мы предполагаем для конструкции из однородного материала, что растягивающие напряжения суммарно равны сжимающим напряжениям и при этом площадь на которую действуют растягивающие напряжения, равна площади, на которую действуют сжимающие напряжения. То определить значение момента сопротивления мы можем следующим образом. Сначала сведем линейно-изменяющиеся нормальные напряжения к равнодействующим, обозначим их как Р:

Р_σс = Р_σр = P = (bh/2)σ/2 = bhσ/4 (10.2)

Тогда момент сопротивления для двух равнодействующих сил, действующих относительно центра тяжести сечения, составит:

W’ = 2Py (10.3)

Как известно на все тела, живые и неживые, в пределах планеты Земля действует сила тяжести. Например, если линейка которую мы все никак не можем доломать, весит 50 г, то это означает, что на линейку действует сила тяжести 0.5 Н или 0.05 кгс. Кроме того, пока никто не опровергнул и предположения, что на каждый отдельный атом, молекулу и любую другую часть материи действует своя сила тяжести, при этом общая сила тяжести линейки равна сумме сил тяжести всех атомов или других частиц, входящих в состав этой линейки. Далее, чтобы линейка не падала на землю под воздействием силы тяжести, мы должны сделать опору для линейки хотя бы в одной точке. Точка эта не простая, получается, что сумма моментов, возникающих при действии сил тяжести, действующих на каждую частицу линейки, в этой точке равна нулю. Таким образом соблюдается условие равновесия системы. Вполне логично эта точка называется центром тяжести. Например, для нашей линейки центр тяжести находится в геометрическом центре линейки. Но сейчас нас интересует центр тяжести не прямоугольника, а треугольника, который символизирует внутренние напряжения или линейно изменяющуюся равномерную нагрузку. Как утверждает наука геометрия, центр тяжести треугольника находится на пересечении медиан углов треугольника, при этом расстояние от любого острого угла до высоты, опущенной на катет, равно 2/3 длины этого катета (рисунок 8.2). Так как мы рассматриваем не все поперечное сечение балки, а только верхнюю (или нижнюю половину), то

у = (h/2)(2/3) = h/3 (10.4)

Теперь, когда мы определили значение плеча силы, мы можем подставить его в формулу (4.3) и определить момент сопротивления для нашей балки прямоугольного сечения относительно оси z:

W’_z = 2(bhσ/4)h/3 = σbh 2 /6 (10.5)

Примечание: как правило момент сопротивления рассматривается как геометрическая характеристика сечения. Т.е. нормальные напряжения в формуле опускаются (W_z = W’_z/σ). Почему, мы узнаем чуть позже.

Момент сопротивления сечения можно определять и как отношение момента инерции относительно оси z к максимальному расстоянию от оси z до наиболее удаленных точек сечения.

W_z = I_z / (h/2) = (bh 3 /12)/(h/2) = bh 2 /6 (10.6)

Итак, в ходе долгих, хотя и не сложных вычислений мы определили, что

М = W’ или M/W’ = 1 или Мσ/W = σ (10.7)

А так как внутренние нормальные напряжения σ должны быть меньше или в крайнем случае равны расчетному сопротивлению материала (σ ≤ R), то формула (4.7) будет иметь несколько иной вид:

М/W = Mσ/W’ ≤ R или W ≥ M/R (10.8)

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Просто благодарна вам за ваш труд, просто восполняю пробелы в знаниях, хотя, имею сертификат конструктора. Сделала небольшой перевод на карту ПБ Украины.

Инна, и вам большое спасибо.

Напишите номер банковские карты

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Момент инерции и момент сопротивления

При определении сечения строительных конструкций очень часто необходимо знать момент инерции и момент сопротивления для рассматриваемого поперечного сечения конструкции. Что такое момент сопротивления и как он связан с моментом инерции изложено отдельно. Кроме того, для сжимаемых конструкций также нужно знать значение радиуса инерции.

Определить момент сопротивления и момент инерции, а иногда и радиус инерции для большинства поперечных сечений простой геометрической формы можно по давно известным формулам:

Таблица 1. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций достаточно простых геометрических форм.

Обычно, этих формул достаточно для большинства расчетов, но случаи бывают всякие и сечение конструкции может быть не такой простой геометрической формы или положение осей, относительно которых нужно определить момент инерции или момент сопротивления, может быть не таким, тогда можно воспользоваться следующими формулами:

Таблица 2. Формы сечения, площади сечений, моменты инерции и моменты сопротивления для конструкций более сложных геометрических форм

Как видно из таблицы 2, высчитывать момент инерции и момент сопротивления для неравнополочных уголков достаточно сложно, да нет в этом необходимости. Для неравнополочных и равнополочных прокатных уголков, а также для швеллеров, двутавров и профильных труб есть сортаменты. В сортаментах значения момента инерции и момента сопротивления приводятся для каждого профиля.

Таблица 3. Изменения моментов инерции и моментов сопротивления в зависимости от положения осей.
Формулы из таблицы 3 могут понадобиться для расчета наклонных элементов кровли.

Источник

Моменты сопротивления.

Моментом сопротивления поперечного сечения относительно какой-нибудь оси зовется отношение момента инерции относительно данной оси к расстоянию наиболее отдаленной точки сечения от этой оси. Обозначим момент сопротивления относительно оси yчерез W_y, а расстояние наиболее отдаленной точки сечения от этой оси через z_max, тогда будем иметь:

(8.34)

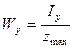
Пользуясь этим правилом, определим моменты сопротивления прямоугольного (рис.8.5), треугольного (рис.8.6), и круглого (рис.8.7) поперечных сечений относительно главных центральных осей yи z.

Для прямоугольного сечения имеем:

, , , , тогда:

, (8.35)

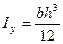
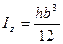
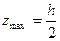
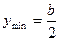
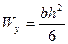
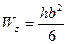
Для треугольного сечения:

, , , , тогда:

, (8.36)

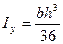
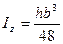
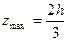
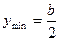
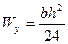
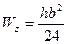
Для круглого сечения:

, , тогда:

(8.37)

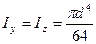
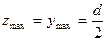
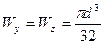
Для поперечного сечения круглой формы определяется полярный момент сопротивления, который равняется отношению полярного момента инерции к радиусу сечения. Учитывая, что

, а , получим:

(8.38)

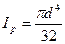
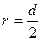
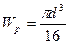
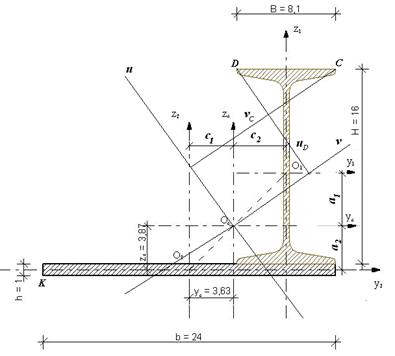
Пример 8.2: Для поперечного сечения, состоящего из двутавра №16 и прямоугольника со сторонами 1 см и 24 см (рис.8.11), требуется:

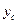
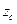
1) определить осевые моменты и центробежный момент инерции относительно центральных осей и ;

2) определить положение главных осей инерции и величины главных осевых моментов инерции;

3) определить главные радиусы инерции и главные моменты сопротивления

Последовательность решения задачи: Учитывая, что положение центра тяжести заданного сечения было уже найдено (смотри пример 8.1), решение задачи осуществляем в такой последовательности:

1) Выписываем геометрические характеристики двутавра №16 (из таблицы ГОСТ 8240-89) и определяем геометрические характеристики прямоугольника с размерами сторон 1х24:

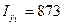
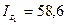
А₁= 20,2 см2; см4; см4;

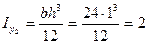
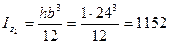
А₂=1·24=24см 2 ; см4;

см4;

2) Определяем расстояния между центральными осями всего сечения и параллельными к ним собственными осями каждой части этого сечения:

см;

см;

см;

см.

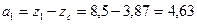
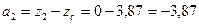
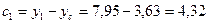
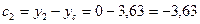
3) Определяем осевые и центробежный моменты инерции сечения относительно центральных осей и :

см 4 ;

см 4 ;

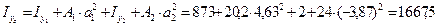
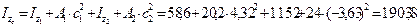
4) Определяем положение главных центральных осей инерции сечения:

;

;

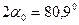
Таким образом, чтобы получить положение главных осей инерции сечения нужно центральные оси повернуть на угол 40,45 0 против часовой стрелки.

Ось максимальной инерции получаем при повороте центральной оси, относительно которой момент инерции имеет больше значения. В данном случае 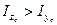, поэтому ось u будет осью максимальной инерции, а перпендикулярная к ней ось v будет осью минимальной инерции.

5) Определяем главные моменты инерции заданного сечения по формулам (8.30):

;

см 4 ;

см 4

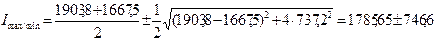
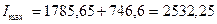
Проверим эти величины. Существует две проверки:

1. сумма моментов инерции относительно двух взаимно перпендикулярных центральных осей остается постоянной величиной при повороте осей, т.е.

;

, это равенство выполняется.

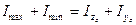
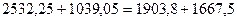
2.Максимальный и минимальный моменты инерции определяем соответственно по формулам (8.26) и (8.25):

,

, где

, , , и

,тогда:

см 4

см 4

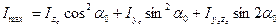
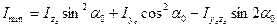
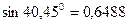
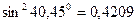
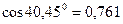
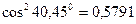
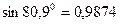
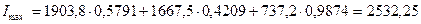
Эти величины полностью совпадают с величинами, определенными по формуле (8.30).

6) Определяем главные радиусы инерции, используя формулы (8.33):

см;

см.

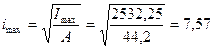
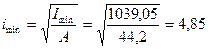
7) Определяем главные моменты сопротивления. Для этого необходимо определить расстояния от главных осей инерции до наиболее отдаленных точек сечения. Рассматривая чертеж сечения, легко заметить, что его точка С больше всего удалена от оси u, а точка D больше всего удалена от оси v. Найдем эти расстояния по формулам (8.24)

,

см, см,

см, см,

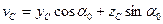
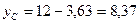
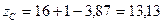
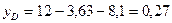
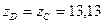
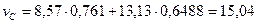
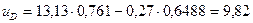
тогда: см,

см

Определяем моменты сопротивления относительно главных центральных осей u и v:

см 3 ;

см 3

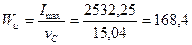
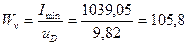
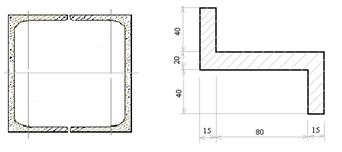
2.8 Задание для самостоятельной работы: 1) Для поперечного сечения балки, составленного из двух прокатных швеллеров № 24, соединенных полками согласно рисунку 8.12, нужно определить геометрические характеристики. 2) Определить геометрические характеристики поперечного сечения, форма и размеры которого (в сантиметрах) показаны на рис.8.13.

Дата добавления: 2018-11-26 ; просмотров: 1034 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник