2пр формула окружности что такое

2 Пи р квадрат это формула

Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:

S=πr 2 – это произведение числа пи на квадрат радиуса.

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .

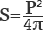
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.

Перевод радиан в градусы.
A_d = A_r * 180 / пи
Где A_d — угол в градусах, A_r — угол в радианах.

Перевод градусов в радианы.
A_r = A_d * пи / 180
Где A_d — угол в градусах, A_r — угол в радианах.

Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.

Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.

Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.

Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.

Площадь сектора.
S = L_d * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, L_d — длина дуги.

Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.

Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.

Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.

Содержание

История [ править | править код ]

Использование многоугольников [ править | править код ]

Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]

Доказательство Архимеда [ править | править код ]

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше [ править | править код ]

Предположим, что площадь круга C больше площади треугольника T = 1 ⁄₂cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈. Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T E&<>=C-T\&<>>G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>> G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>»/>

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄₂nhs. Но h 1 ⁄₂cr, получили противоречие.

Не меньше [ править | править код ]

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника P_n должна быть меньше T.

G_ \P_ &<>=C+G_ \&<> D = T − C > G n P n = C + G n C + D P n T =T-C\&<>>G_ \P_ &<>=C+G_ \&<> G_ \P_ &<>=C+G_ \&<>

Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.

Таким образом, площадь круга в точности равна площади треугольника.

Доказательство перегруппировкой [ править | править код ]

многоугольник			параллелограмм
n	сторона	основание	высота	площадь
4	1,4142136	2,8284271	0,7071068	2,0000000
6	1,0000000	3,0000000	0,8660254	2,5980762
8	0,7653669	3,0614675	0,9238795	2,8284271
10	0,6180340	3,0901699	0,9510565	2,9389263
12	0,5176381	3,1058285	0,9659258	3,0000000
14	0,4450419	3,1152931	0,9749279	3,0371862
16	0,3901806	3,1214452	0,9807853	3,0614675
96	0,0654382	3,1410320	0,9994646	3,1393502
∞	1/∞	π	1	π

Интегрирование [ править | править код ]

Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.

Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:

Быстрая аппроксимация [ править | править код ]

Метод удвоения Архимеда [ править | править код ]

Если задан круг, пусть u_n будет периметром вписанного правильного n-угольника, а U_n — периметром описанного правильного n-угольника. Тогда u_n и U_n являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (u_n + U_n)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить u_n и U_n для больших n, Архимед вывел следующие формулы:

u 2 n = U 2 n u n = u_ >>> (среднее геометрическое) U 2 n = 2 U n u n U n + u n = u_ > +u_ >>> (среднее гармоническое).

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.

В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u₆ = 6, а описанный шестиугольник имеет периметр U₆ = 4√3. Удваиваем семь раз, получаем

knu_nU_n(u_n + U_n)/466,00000006,92820323,23205081126,21165716,43078063,16060942246,26525726,31931993,14614433486,27870046,29217243,14271824966,28206396,28542923,141873351926,28290496,28374613,141662863846,28311526,28332553,141610277686,28316786,28322043,1415970

Улучшение Снелла-Гюйгенса [ править | править код ]

Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:

Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.

Развитие формулы удваивания Архимеда [ править | править код ]

В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+ 1 ⁄₂c_n, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена

Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону S_n, тогда отношение превращается в S_n : s_n = 1 : 1 ⁄₂c_n. (Мы снова используем факт, что OP равен половине A′B.) Получаем

Обозначим периметр вписанного многоугольника через u_n = ns_n, а описанного через U_n = nS_n. Комбинируя равенства, получим

Можно также вывести

Аппроксимация случайными бросаниями [ править | править код ]

Конечная перегруппировка [ править | править код ]

Обобщения [ править | править код ]

Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.

Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π /4, и отношение площади эллипса к площади прямоугольника будет тоже π /4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — π ab/4.

Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.

Источник

Как найти радиус окружности

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Источник

Длина окружности

Длина окружности

Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):

Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:

где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.

Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.

Задачи на длину окружности

Задача 1. Найти длину окружности, если её диаметр равен 5 см.

Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:

Задача 2. Найти длину окружности, радиус которой равен 3,5 м.

Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:

теперь найдём длину окружности, умножив π на диаметр:

Задача 3. Найти радиус окружности, длина которой равна 7,85 м.

Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:

следовательно, радиус будет равен:

R	≈	7,85	=	7,85	= 1,25 (м).
		2 · 3,14		6,28

Задачи на площадь круга

Задача 1. Найти площадь круга, если его радиус равен 2 см.

Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).

Задача 2. Найти площадь круга, если его диаметр равен 7 см.

Решение: Сначала найдём радиус круга, разделив его диаметр на 2:

теперь вычислим площадь круга по формуле:

S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).

Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:

S = π	D 2	≈ 3,14 ·	7 2	= 3,14 ·	49	=
	4		4		4

=	153,86	= 38,465 (см 2 ).
	4

Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:

Источник

Урок 25 Бесплатно Длина окружности и площадь круга

На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.

Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.

Узнаем, как рассчитать длину окружности и площадь круга.

Окружность и круг

Мы часто встречаем такие понятия, как окружность и круг.

Давайте попробуем разобраться, что называют окружностью, а что кругом.

Центр окружности— это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.

Свои имена окружность и круг приобрели не сразу.

В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.

Только в Древней Греции окружность и круг приобрели себе свои названия.

Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.

У меня есть дополнительная информация к этой части урока!

Древние греки считали круг и окружность символом бесконечности и совершенства. Поражало то, что в каждой своей точке окружность устроена одинаково, представляя собой бесконечную линию, которая движется сама по себе.

У древних славян еще за долго до христианства круг был символом солнца.

Символика круга в различных религиях сопоставляется с целостностью, вечностью и бесконечной мудростью.

У буддистов круг символизирует единство внутреннего и внешнего мира.

В христианстве круг служит эталоном божественного и духовного совершенства.

В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.

Рассмотрим подробней элементы, характерные для окружности.

Радиус окружности— это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.

С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.

Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.

Радиус обозначается маленькой латинской буквой (r) или заглавной (R).

В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.

Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.

По величине диаметр равен двум радиусам, лежащим на одной прямой.

d = 2r

Следовательно, радиус- это половина диаметра.

r = d: 2

Пример 1

Радиус окружности равен 6 см.

Чему равен диаметр окружности?

r = 6 см

Решение:

d = 2r

d = 2r= 2*6 = 12 (см) диаметр окружности

Ответ: d= 12 см

Пример 2

Диаметр окружности равен 12 см.

Чему равен радиус окружности?

d = 12 см

Решение:

r = d : 2

r = 12 : 2 = 6 (см) радиус окружности

Ответ: r = 6 см

У меня есть дополнительная информация к этой части урока!

Образовались две дуги: \(\mathbf<\cup AB\ и\ \cup BA>\)

Отрезок, который соединяет любые две точки на окружности (отрезок секущей), называется хордой.

На рисунке отрезок MN является хордой.

Если хорда проходит через центр окружности, то она является самой большой хордой для этой окружности. По своей сути она является диаметром для данной окружности и делит окружность на две равные дуги.

По мере удаления хорды от центра размеры ее уменьшаются, а дуги делятся на большую и малую.

АВ— самая большая хорда окружности- диаметр окружности.

CD, N₁M_1, NM, FE— хорды окружности.

Хорды окружности, удаленные на равные расстояния от центра, равны.

Хорды NM и N₁M₁ равны.

Если две хорды пересекаются в точке, то их отрезки пропорциональны.

Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.

Пройти тест и получить оценку можно после входа или регистрации

Длина окружности и площадь круга

Давайте выясним, что такое длина окружности и как ее определить.

Представьте, что окружность обернута нитью.

Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.

Обычно длина окружности обозначается заглавной буквой С

Длина окружности (С) зависит от длины ее диаметра (d)

Обратите внимание на рисунок.

Вы можете заметить, что чем больше диаметр, тем больше длина окружности.

Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.

А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.

Это число (коэффициент пропорциональности) обозначают греческой буквой \(\mathbf<\pi>\), читается «пи».

С— это длина окружности

d— диаметр окружности

запишем отношение \(\mathbf\)

отсюда следует, что длина окружности равна

Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности

Число \(\mathbf<\pi>\)- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.

У меня есть дополнительная информация к этой части урока!

История числа \(\mathbf< \pi>\) насчитывает около 4 тысячелетий.

Одно из первых доказательств древнего существования этого числа \(\mathbf< \pi>\) заключено в папирусе Ахмеса, в одном из старейших задачников (1650 год до н.э.), найденного в Древнем Египте.

В папирусе дано достаточно точное, особенного для того времени, значение числа, равного 3,1605.

Точнее число \(\mathbf< \pi>\) рассчитал древнегреческий математик Архимед. Он приближенно представил значение константы в виде обыкновенной дроби \(\mathbf<\frac <22><7>>\)

Архимеду удалось найти точное приближение числа \(\mathbf< \pi>\) (т.е. узкий числовой промежуток к которому принадлежит число \(\mathbf< \pi>\)).

Пройти тест и получить оценку можно после входа или регистрации

Решения задач по теме «Длина окружности и площадь круга»

Рассмотрим примеры решения задач

Задача 1

Найдите длину окружности, если ее радиус равен 4 см.

Число \(\mathbf<<\pi>>\) округлите до сотых.

r = 4 см

Решение:

Подставив в формулу известные значения радиуса и постоянной \(\mathbf<\pi>\), получим:

Ответ: \(\mathbf\)(см)

Задача 2

Длина окружности надувного бассейна 15,7м.

Найдите диаметр этого бассейна.

Число \(\mathbf<\pi>\) округлите до сотых.

C = 15,7 м

Решение:

Подставив в формулу известные значения длины окружности и постоянной \(\mathbf<\pi>\), получим:

Ответ: \(\mathbf\) (м)

Задача 3

Диаметр окружности равен 6 см.

Найдите площадь круга, ограниченного этой окружностью.

Значение числа \(\mathbf<\pi>\) округлить до сотых.

d = 6 cм

Решение:

\(\mathbf<4><\cdot>3,14<\cdot>6^2 = \frac <3,14<\cdot>36> <4>> = 3,14<\cdot>9=28,26\) (cм 2 ) площадь круга

Ответ: \(\mathbf\) (см 2 )

Задача 4

Вычислите площадь полукруга, если радиус круга равен 5 см.

Значение \(\mathbf<\pi >\) округлить до целых.

r = 5 cм

Решение:

Площадь круга найдем по формуле:

Площадь полукруга будет равна половине площади всего круга.

Следовательно, формула для расчета площади полукруга получится вида:

Подставим в формулу известные значения радиуса круга и постоянной \(\mathbf<\pi>\), получим:

\(\mathbf <2>=37,5>\) (cм 2 ) площадь полукруга

Ответ: \(\mathbf\) (см 2 )

Задача 5

Найдите площадь круга, если известна длина окружности С.

Длина окружности С

Решение:

Длина окружности выражается формулой:

Выразим неизвестный радиус окружности через длину окружности:

Площадь круга определяем по формуле:

Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:

Сократим полученную дробь:

У меня есть дополнительная информация к этой части урока!

Кроме вычислительных задач, существуют задачи на построение окружности и круга.

Окружность и круг можно начертить с помощью чертежного инструмента, который называется циркуль.

В переводе с латинского языка circulus означает «окружность», «круг».

Циркуль использовали еще с древности, много тысяч лет назад, об этом свидетельствуют найденные на раскопках находки, изображения.

Циркуль представляет собой две одинаковые по длине «ножки». На конце одной из них игла, а на второй- грифель.

Есть циркуль, у которого вместо «ножки» с грифелем помещается карандаш.

Рассмотрим, как построить окружность (круг) на бумаге с помощью циркуля и линейки.

Если задан радиус окружности (круга), то в нулевую отметку на линейке ставим иголку циркуля, другая «ножка» циркуля с грифелем в точку на линейке, равной по значению заданному радиусу.

Не отрывая грифеля второй «ножки» циркуля от бумаги проводим окружность с заданным радиусом.

Если в задаче задан диаметр, то, прежде чем совершать замер по линейке, необходимо диаметр разделить пополам.

Таким образом, устанавливаем раствор циркуля по линейке на расстояние d:2 = r и чертим окружность по выше изложенной схеме.

Данный способ построения окружности (круга) может быть применен и на бумаге, если под рукой не оказалось циркуля.

В качестве колышка берется кнопка, к ней привязывается нить определенной длинны (длина нити равна значению заданного радиуса), ко второму концу привязывается карандаш

Пройти тест и получить оценку можно после входа или регистрации

Источник