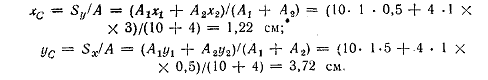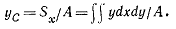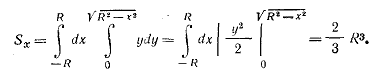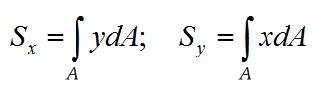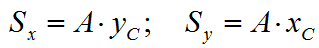3 что такое статический момент площади
СОПРОМАТ ОН-ЛАЙН
Меню сайта
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Базовый курс лекций по сопромату, теория, практика, задачи.
1. Геометрические характеристики сечений.
1.1. Статический момент сечения.
При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.
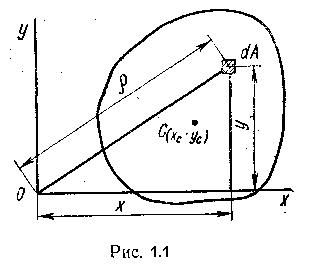
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида
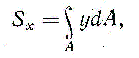
Единицей измерения статического момента является единица длины в третьей степени, обычно см 3 (см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать
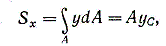
Из формулы (1.2) следует формула определения ординаты центра тяжести
Аналогично, статический момент относительно оси у равен
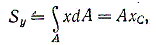
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.
Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.
Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.
Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.
Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:
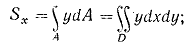
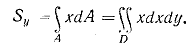
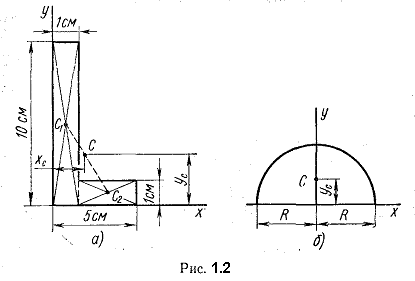
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.
Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.
По формулам (1.3) и (1.5) получим:
Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).
Решение. Пользуемся формулой
Вычисляем числитель, используя уравнение окружности х 2 + y 2 = R 2 :
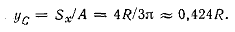
6.1. Статический момент площади сечения
6.1. СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ
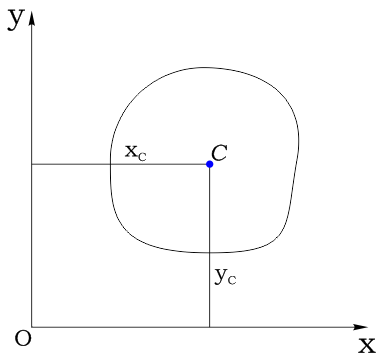
Статический момент площади – распространенная на всю площадь сумма произведений элементарных площадок dA на расстояние от них до этой оси Это понятие аналогично моменту силы относительно оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент Sz – это момент силы тяжести пластины относительно оси z. Размерность: единицы длины в третьей степени (см3; м3). Знаки: плюс, ноль и минус. Ось центральная – ось, относительно которой статический момент площади равен нулю. Центр тяжести сечения – точка пересечения центральных осей. Если фигура имеет ось симметрии, то эта ось является центральной. Статический момент составного сечения равен сумме статических моментов элементов этого сечения. Это следует из свойства определенного интеграла, который можно вычислять по частям – свойство аддитивности (от англ. add – прибавлять, присоединять, складывать). При известных статических Рис. 6.2. Связь знака статического момента площади с его положением в координатной системе моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры: Пример 6.1. Определить положение центральных осей, параллельных основанию и высоте фигуры. Решение Разбиваем сложную фигуру на две простые, в конкретном примере – на два прямоугольника. Их центры тяжести расположены посредине высоты и посредине ширины. Координаты центров тяжести и площади простых фигур Статические моменты площадей простых фигур Координаты центра тяжести составной фигуры Через найденную точку проводим центральные оси zC и yC, параллельные основанию фигуры и ее высоте. Примечание. Центр тяжести фигуры, составленной из двух частей, лежит на линии, соединяющей центры тяжести простых фигур ее составляющих, причем расстояния до них обратно пропорциональны площадям простых фигур. Если сложная фигура составлена из нескольких простых, то общий центр тяжести находится внутри многоугольника, вершинами которого являются центры тяжести простых фигур.
iSopromat.ru
Формулы для расчета геометрической характеристики статического момента сечений, плоских фигур и площади:
Рассмотрим сечение (плоскую фигуру) произвольной формы площадью A:
Выделим в нем элементарную площадку dA и зададим систему координат:
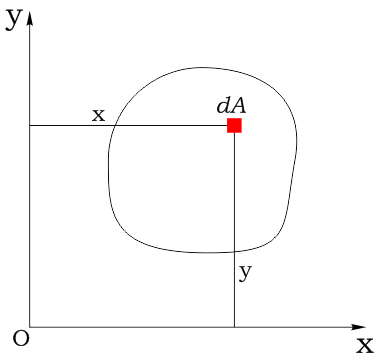
Координаты площадки обозначим соответственно как x и y:
Статический момент элементарной площадки:
Суммируя выражения по всей площади фигуры, получим соответственно:
Единица измерения статического момента [м 3 ].
тогда статические моменты относительно осей x и y:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Набор студента для учёбы
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Статический момент площади
При некоторых деформациях прочность деталей зависит не только от площади поперечного сечения, но и от его формы. До сих пор мы изучали деформации, у которых напряжения зависели только от площади поперечного сечения. В дальнейшем для изучения деформаций кручения и изгиба нам потребуется знание некоторых других геометрических характеристик плоских фигур.
Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на расстояния от них до этой оси (рис. 3.1).
Статический момент площади обозначим S с индексом соответствующей оси:

Формулы для определения координат центра тяжести площади фигуры:

Так как в формулах (3.2) под А можно понимать площадь dA элементарной площадки, то в пределе при dA, стремящемся к нулю, выражения, стоящие в числителях правых частей формул, будут представлять собой статические моменты площади фигуры относительно осей у и х, а 

Статический момент площади фигуры может быть величиной положительной, отрицательной и равной нулю. Очевидно, что статический момент площади относительно оси, проходящей через центр тяжести площади фигуры (центральной оси), в том числе относительно оси симметрии фигуры, равен нулю.

где Si – статический момент площади каждой части фигуры.
Статические моменты и координаты центра тяжести
Вычисление статических моментов и координат центра тяжести кривой
Если же эти точки расположены по разные стороны от оси, то для точек, находящихся по одну сторону оси, расстояния берутся положительными, а для точек по другую сторону от оси — отрицательными.
Поэтому если точки расположены на координатной плоскости,
Так как на отрезке выполняется неравенство
Как формула (1), так и формула (2) верны и в случае, когда кривая пересекает оси координат.
в) Введем понятие центра тяжести.
Обозначим через и расстояния центра тяжести кривой от осей ординат и абсцисс.
Тогда, пользуясь определением центра тяжести кривой, получим:
Замечание. Если кривая расположена симметрично относительно некоторой прямой, то центр тяжести такой кривой находится на этой прямой.
Это замечание позволяет в некоторых случаях упростить нахождение координат центра тяжести плоской кривой.
Пример 1. Найти статический момент полуокружности относительно диаметра.
Вычисление проще провести, перейдя к параметрическим уравнениям окружности. Так как ее радиус равен двум, то для четверти окружности имеем:
Отсюда находим, что и
Вычисление статических моментов и координат центров тяжести плоских фигур
(части фигуры, расположенные ниже оси абсцисс, дают отрицательный вклад в ).
Пример 3. Найти статический момент (относительно оси ) фигуры, ограниченной осью абсцисс и одной аркой циклоиды: