дискретное представление информации двоичные числа двоичное кодирование текста в памяти компьютера
Билеты №3
1. Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный объем текста.
Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр 0 и 1. Эти два символа принято называть двоичными цифрами или битами. С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:
0 – отсутствие электрического сигнала;
1 – наличие электрического сигнала.
Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
Вам приходится постоянно сталкиваться с устройством, которое может находится только в двух устойчивых состояниях: включено/выключено. Конечно же, это хорошо знакомый всем выключатель. А вот придумать выключатель, который мог бы устойчиво и быстро переключаться в любое из 10 состояний, оказалось невозможным. В результате после ряда неудачных попыток разработчики пришли к выводу о невозможности построения компьютера на основе десятичной системы счисления. И в основу представления чисел в компьютере была положена именно двоичная система счисления.
Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции).
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.
Непозиционные системы счисления.
Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.
MCMXCVIII = 1000+(1000-100)+(100-10)+5+1+1+1 = 1998
Позиционные системы счисления.
Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла она в древнем Шумере. Некоторые учёные полагают, что такая система возникала у них из подсчёта фаланг на руке большим пальцем. Широкое распространение получила двенадцатеричная система счисления в XIX веке.
Билет 3. Дискретное представление информации: двоичные числа, двоичное кодирование текста в памяти компьютера



Дискретное представление информации: двоичные числа, двоичное кодирование текста в памяти компьютера. Информационный объем текста.
План ответа
1. Дискретное представление информации.
3. Двоичное кодирование текста.
4. Информационный объем текста. Дискретное представление информации
Вся информация, которая попадает в компьютер, преобразуется в последовательность электрических импульсов. Наличие импулк»! са принято условно обозначать «1», а его отсутствие — «О». ТаИЯ способ кодирования информации называется двоичным или бинарм ным. Один двоичный символ получил название бит. (bit — от щШ лийского bjnary digit — «двоичная цифра»). Таким образом, двоичное кодирование — это представление информации при помощи ми* J нимально возможного числа элементарных символов.
С точки зрения инженеров двоичное кодирование привлекательно тем, что легко реализуется технически. Электронные схемы дл
• электромагнитные реле (замкнуто/разомкнуто), которые широко использовались при конструировании первых ЭВМ;
• поверхности магнитных носителей информации (намагничено/размагничено);
• поверхности лазерных дисков (отражает/не отражает);
• триггер, который может находиться в одном из двух состояний (О или 1), широко используется в оперативной памяти компьютере.
Таким образом, в компьютерах используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т. п.), а не, например, с десятью, — как в десятичной;
• представление информации посредством только двух состояний надежно и помехоустойчиво;
• возможно применение аппарата алгебры логики для выполнения логических преобразований информации;
• двоичная арифметика намного проще десятичной.
Двоичные числа
Двоичное кодирование автоматически дает способ кодирования чисел в двоичной системе счисления.
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее.положения (позиции) в последовательности цифр, изображающих число.
Наиболее употребительными в настоящее время являются десятичная и двоичная позиционные системы счисления.
Десятичная система счисления имеет алфавит, состоящий из 10 цифр (соответственно основание этой системы счисления равно 10): 0,1,2, 3,4, 5, 6,7, 8, 9. Информацию несет не только сама цифра, но и то место, на котором она стоит (ее позиция в числе). Например, в десятичном числе 444 и количество единиц, и количество десятков, и количество сотен обозначается одинаковыми цифрами. А вот в числе 700 значима только первая цифра — 7, обозначающая количество сотен, а две цифры 0 нужны лишь для обозначения позиции цифры 7 и сами по себе вклад в число не дают.
Таким образом, числа в позиционных системах счисления записываются в виде суммы степеней основания, при этом в роли коэффициентов выступают цифры данного числа.
Двоичное кодирование текста
Традиционно для кодирования одного символа используется количество информации, равное 1 байту (8 битам). Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код (или соответствующий ему двоичный код). Код символа хранится в памяти компьютера, где занимает, как уже говорилось, 1 байт. При таком способе можно закодировать 256 различных символов (256 = 2 8 ). Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и заглавные буквы русского алфавита, цифры, знаки, графические символы и т.д.
Для разных типов ЭВМ и операционных систем используются различные таблицы кодировки, отличающиеся порядком размещения символов алфавита в кодовой таблице.
В настоящее время существует несколько различных кодировок (кодовых таблиц) для русских букв. Каждая кодировка задается своей кодовой таблицей. Одному и тому же двоичному коду в различных кодировках соответствуют различные символы. Поэтому если текст создан в одной кодировке, то он не будет правильно отображаться в другой.
Присвоение символу конкретного кода является вопросом соглашения, которое и фиксируется в конкретной кодовой таблице. В качестве международного стандарта принята кодовая таблица ASCII. В этой кодовой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов.
Стандартными в этой таблице кодов ASCII являются только перввые 128 символов, т. е. символы с номерами от нуля (двоичный ко 00000000) до 127 (01111111). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, начиная со 128 (двоичный код 10000000 и кончая 255 (11111111), используются для кодировки букв национальных алфавитов, символов псевдографики и научных символов Одним из первых стандартов кодирования русских букв на компьютерах был КОИ8 (код обмена информацией, 8-битный). Эта кодировка применялась еще в 1970-е годы на компьютерах серии ЕС ЭВМ Операционная система MS DOS использует кодировку СР866. Наиболее распространенной в настоящее время является кодирошг MS Windows, которая обозначается как СР1251, или Windows 1251, В настоящее время все большее число программ начинает поддерживать стандарт Unicode, который позволяет кодировать практически все языки и диалекты жителей Земли. Этот стандарт отводит на каждый символ не один байт, а два, поэтому с его помощью можно закодировать 65 536 различных символов (65 536 = 2 16 ).
Информационный объем текста
В качестве примера рассмотрим следующую задачу. Пусть требуется определить, какой объем информации содержит реферат, ни» бранный на компьютере и содержащий 88 страниц, если на каждой странице 50 строк, а в каждой строке — в среднем 60 символов.
Одна страница будет содержать 50 х 60 = 3000 байт информации. Объем всей информации в реферате: 3000 х 88 = 264000 байт, или в более крупных единицах: 264000 : 1024 = 257,8125 кбайт.
Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный обьем текста
Ответ:
Для записи текстовой (знаковой) информации всегда используется какой-либо язык (естественный или формальный). Всё множество используемых в языке символов называется алфавитом. Полное число символов алфавита называют его мощностью. При записи текста в каждой очередной позиции может появиться любой из N символов алфавита, т.е. может произойти N событий. Следовательно, каждый символ алфавита содержит iбит информации, где i определяется из неравенства: 2 i ≥ N. Тогда общее количество информации в тексте определяется формулой:
Билет 4
Дискретное представление информации: кодирование цветного изображения в компьютере (растровый подход). Представление и обработка звука и видеоизображения. Понятие мультимедиа.
Ответ:
Растровая графика.
Графическая информация может быть представлена дискретно. Для этого изображение разбивают на отдельные маленькие фрагменты (пиксели), затем каждому пикселю присваивается код цвета (считаем, что весь пиксель целиком одноцветный, а изображение в целом мозаика мелких цветных точек). Этот процесс называют пространственной дискретизацией изображения.
Качество такого изображения зависит от двух параметров. Качество выше при меньшем размере пикселя и большем количестве используемых цветов (или оттенков серого, для монохромного изображения). Полный набор цветов, которые можно использовать для создания изображения называется палитрой. Изображение, сформированное таким способом, называют растровым. Формула для определения количества информации в нём имеет вид:
| Номер | Цвет | Яркость | Красный | Зеленый | Синий |
| Черный | |||||
| Синий | |||||
| Зеленый | |||||
| Голубой | |||||
| Красный | |||||
| Фиолетовый | |||||
| Коричневый | |||||
| Белый | |||||
| Серый | |||||
| Светло-синий | |||||
| Светло-зеленый | |||||
| Светло-голубой | |||||
| Светло-красный | |||||
| Светло-фиолетовый | |||||
| Желтый | |||||
| Ярко-белый |
Векторная графика.
Отметим также, что рассмотренный выше способ представления изображений не единственный. Можно представить изображение совокупностью простых геометрических фигур (прямых линий, окружностей, эллипсов, дуг, прямоугольников и т.д.) графических примитивов и записать информацию о координатах и параметрах каждого их них. При этом координатная сетка должна совпадать с сеткой пикселей на экране. Такой способ представления изображений называют векторной графикой. На рисунке показаны примеры графических примитивов:
Такой способ представления изображения дает возможность получить файл малого размера. Качество изображения не изменяется с изменением размера рисунка, но даже профессиональные векторные графические редакторы не могут обеспечить качество графики, сравнимое с растровыми изображениями.
Видеоинформация.
Дискретное представление информации двоичные числа двоичное кодирование текста в памяти компьютера
Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации
Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.
Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.
Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.
Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.
Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.
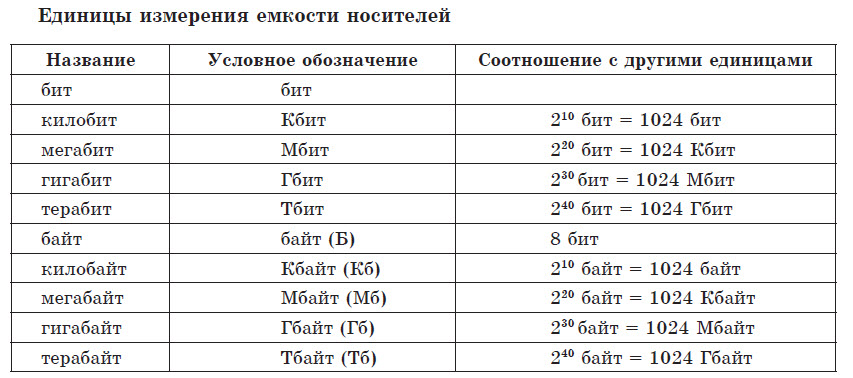
Единицы измерения количества информации
Основной единицей хранения и обработки цифровой информации принят байт.
Соответственно, с помощью одного байта можно получить 256 (= 2 8 ) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.
На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 2 10 ).
Системы счисления
Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.
Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.
Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.
Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.
В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.
Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.
В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.
Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.
Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.
Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.
348 = 3 • 10 2 + 4 • 10 1 + 8 • 10 0
–348,17 = –(3 • 10 2 + 4 • 10 1 + 8 • 10 0 + 1 • 10 –1 + 7 • 10 –2 )
Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:
316 — число в десятичной системе счисления,
3168 — число в восьмеричной системе счисления.
Свойства записи чисел в позиционной системе счисления:
Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.
Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.
В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а1, а2, а3 и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:
Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.
Представление числа в виде многочлена называют развернутой записью числа:
Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:
Конспект урока по информатике «Дискретная форма представления информации».
Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный объем текста
1. Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный объем текста.
Человек воспринимает информацию с помощью органов чувств. При этом он стремится зафиксировать ее и представить в форме, доступной другим. Форма представления информации может быть различной. Один и тот же объект, например дом, можно изобразить графически в виде рисунка или выполнить чертеж в трех проекциях. Его можно описать в стихах или с помощью математических формул.
Форма представления информации зависит от цели, для которой она служит. Например. Запись решения квадратного уравнения на алгоритмическом языке или языке программирования в корне отличается от той формы записи, которая используется на уроках алгебры.
Рассмотрим представления чисел.
Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Все системы счисления делятся на позиционные и непозиционные.
Система счисления – это способ записи чисел с помощью специальных знаков – цифр.
Числа: 123, 45678, 1 CXL
Цифры: 0, 1, 2, … I, V, X, L, …
Алфавит – это набор цифр.
Типы систем счисления:
- непозиционные – значение цифры не зависит от ее места (позиции) в записи числа; позиционные – зависит от ее места (позиции) в записи числа.
Унарная – одна цифра обозначает единицу (1 день,
1 камень, 1 баран, …)
Римская: I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони), L – 50,
C – 100 (Centum), D – 500 (Demimille),
M – 1000 (Mille)
Позиционная система: значение цифры определяется ее позицией в записи числа.
Десятичная система: первоначально – счет на пальцах
изобретена в Индии, заимствована арабами, завезена в Европу
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
3 7 8 = 3·102 + 7·101 + 8·100
Другие позиционные системы:
• двоичная, восьмеричная, шестнадцатеричная (информатика)
• двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
• двадцатеричная (1 франк = 20 су)
• шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
Cистемы счисления в компьютерах
В XVII веке немецкий ученый Готфрид Лейбниц предложил уникальную систему представления чисел с помощью всего двух символов – 0 и 1. Сегодня этот способ повсеместно используется в технике, в том числе и в компьютерах и называется дискретным.
Компьютер способен хранить только дискретно представленную информацию. Его память, как бы велика она ни была, состоит из отдельных битов, а значит, по своей сути дискретна.

Двоичная кодировка (двоичная система счисления) имеет ряд преимуществ перед другими системами кодирования:
Для ее реализации нужны технически не сложные элементы с двумя возможными состояниями (есть ток — нет тока, намагничен — не намагничен и т. д.). Представление информации посредством только двух состояний надежно и помехоустойчиво. Возможно применение особой алгебры логики (булевой алгебры) для выполнения логических преобразований информации. Двоичная арифметика намного проще десятичной. Двоичные таблицы сложения и умножения предельно просты.
- Обработка информации в компьютере основана на обмене электрическими сигналами между различными устройствами машины. Признак наличия сигнала можно обозначить цифрой 1, признак отсутствия — цифрой 0.
ДВОИЧНОЕ КОДИРОВАНИЕ ТЕКСТА
Для представления текста в компьютере используется 256 различных знаков. Для кодирования 1 знака отводится 8 битов.
Кодирование – присвоение каждому символу десятичного кода от 0 до 255 или соответствующего ему двоичного кода от до
Присвоение символу определенного кода – это вопрос соглашения, которое фиксируется в кодовой таблице.
В качестве международного стандарта была принята кодовая таблица ASCII (American Standard Code for Information Interchange) :
Коды с 33 по 127 – интернациональные, соответствуют символам латинского алфавита, цифрам, знакам арифметических операций, знакам препинания;
Коды с 128 по 255 – национальные, т. е. кодировка национального алфавита.
на 1 символ отводится 1 байт (8 бит), всего можно закодировать 28 = 256 символов
С 1997 года появился новый международный стандарт Unicode, который отводит для кодировки одного символа 2 байта (16 бит), и можно закодировать 65536 различных символов (Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, множество математических, музыкальных, химических и прочих символов)
В настоящий момент существует пять кодировок кириллицы: КОИ-8, CP1251, CP866, ISO, Mac. Для преобразования текстовых документов из одной кодировки в другую существуют программы которые называются Конверторы
Чтобы подсчитать информационный объем текста необходимо количество информации, которое несет один символов, умножить на количество символов в тексте: