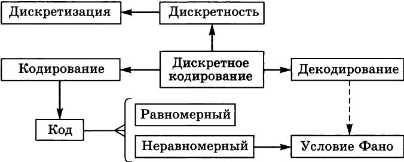
для кодирования какого вида информации требуется дискретизация

Содержание урока

Выводы. Интеллект-карта

Выводы
Интеллект-карта

• Дискретизация — это представление непрерывного объекта в виде множества отдельных элементов.
• Компьютеры обрабатывают информацию в двоичном коде, в котором используется два знака (обычно 0 и 1).
• Данные, с которыми работает компьютер, — дискретные. Для того чтобы информацию можно было обрабатывать с помощью компьютеров, её нужно дискретизировать — перевести в дискретный вид. Как правило, дискретизация приводит к потере части информации.
• Равномерный код — это код, в котором все кодовые слова имеют одинаковую длину.
• При равномерном кодировании длину кодовых слов L выбирают из условия M L ≥ M₀, где М₀ — мощность алфавита исходного сообщения и М — мощность нового алфавита.
• Неравномерный код — это код, в котором кодовые слова имеют различную длину.
• Декодирование — это восстановление исходного сообщения из кода.
• Сообщения, закодированные с помощью неравномерного кода, не всегда можно декодировать однозначно.
• Неравномерный код декодируется однозначно, если выполняется условие Фано: ни одно кодовое слово не совпадает с началом другого кодового слова.
• С помощью i бит можно закодировать 2 i различных сообщений.

Рис. 2.8

Какие сведения из параграфа вы бы добавили в эту схему?

Следующая страница Вопросы и задания

Cкачать материалы урока

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 17.

Тема — Кодирование графической и звуковой информации

Большую часть информации человек получает с помощью зрения и слуха. Важность этих органов чувств обусловлена развитием человека как биологического вида, поэтому человеческий мозг с большой скоростью способен обрабатывать огромное количество графической и звуковой информации.

С появлением компьютеров возникла огромная потребность научить их обрабатывать такую информацию. Как же такую информацию может обработать компьютер?

Итак, кодирование графической информации осуществляется двумя различными способами: векторным и растровым

Программы, работающие с векторной графикой, хранят информацию об объектах, составляющих изображение в виде графических примитивов: прямых линий, дуг окружностей, прямоугольников, закрасок и т.д.

Достоинства векторной графики:

— Преобразования без искажений.

— Маленький графический файл.

— Рисовать быстро и просто.

— Независимое редактирование частей рисунка.

— Высокая точность прорисовки.

— Редактор быстро выполняет операции.

Недостатки векторной графики:

— Векторные изображения выглядят искусственно.

— Ограниченность в живописных средствах.

Программы растровой графики работают с точками экрана (пикселями). Это называется пространственной дискретизацией.

КОДИРОВАНИЕ РАСТРОВОЙ ГРАФИКИ

Давайте более подробно рассмотрим растровое кодирование информации.

Компьютер запоминает цвет каждой точки, а пользователь из таких точек собирает рисунок.

При этом зная количество пикселей по вертикале и горизонтали, мы сможем найти — разрешающую способность изображения.

Разрешающая способность находится по формуле:

где n, m — количество пикселей в изображении по вертикали и горизонтали.

В процессе дискретизации каждый пиксель может принимать различные цвета из палитры цветов. При этом зная количество цветов, которые можно использовать в палитре и воспользовавшись формулой Хартли, мы сможем найти количество информации, которое используется для кодирования цвета точки, что мы будем называть глубиной цвета.

где N — количество цветов в палитре;

Таким образом, чтобы найти вес изображения достаточно перемножить разрешающую способность изображения на глубину цвета: L=P*i.

Каким именно образом возможно закодировать пиксель? Для этого используются кодировочные палитры.

КОДИРОВОЧНАЯ ПАЛИТРА RGB

Когда художник рисует картину, цвета он выбирает по своему вкусу. Но цвет в компьютере надо стандартизировать, чтобы его можно было распознать. Поэтому надо определить, что такое каждый цвет.

В экспериментах по производству цветных стекол М. В. Ломоносов показал, что получить любой цвет возможно, используя три различных цвета.

Этот факт был обобщен Германом Грассманом в виде законов аддитивного синтеза цвета.

Давайте рассмотрим два из этих законов:

— Закон трехмерности. С помощью трех независимых цветов можно, смешивая их в однозначно определенной пропорции, выразить любой цвет.

— Закон непрерывности. При непрерывном изменении пропорции, в которой взяты компоненты цветовой смеси, получаемый цвет также меняется непрерывно.

Из биологии вы знаете, что рецепторы человеческого глаза делятся на две группы: палочки и колбочки. Палочки более чувствительны к интенсивности поступаемого света, а колбочки — к длине волны.

Если посмотреть, как распределяется количество колбочек по тому, на какую длину волны они «настроены», то количество колбочек «настроенных» на синий, красный и зеленый цвета окажется больше.

Поэтому такие цвета были взяты основными для построения цветовой модели, которая получила название RGB (Red, Green, Blue). То есть задавая количество любого из этих трех цветов, можно получить любой другой. Для кодирования каждого цвета было выделено 8 бит (режим True-Color). Таким образом, количество каждого цвета может изменяться от 0 до 255, часто это количество выражается в шестнадцатеричной системе счисления (от 0 до FF).

Так как описание цвета происходит определением трех величин, то это наводит на мысль считать их координатами точки в пространстве. Получается, что координаты цветов заполняют куб.

При этом яркость цвета определяется тем насколько близка к максимальному значению хотя бы одна координата из трех.

КОДИРОВАНИЕ ЗВУКОВОЙ ИНФОРМАЦИИ

Давайте перейдем к кодированию звуковой информации.

Из курса физики вам всем известно, что звук — это непрерывная волна с изменяющейся амплитудой и частотой.

Для того, чтобы компьютер мог обрабатывать непрерывный звуковой сигнал, он должен быть дискретизирован, т. е. превращен в последовательность электрических импульсов (двоичных нулей и единиц).

Для этого звуковая волна разбивается на отдельные временные участки.

Гладкая кривая заменяется последовательностью «ступенек». Каждой «ступеньке» присваивается значение громкости звука. Чем больше количество уровней громкости, тем больше количество информации будет нести значение каждого уровня и более качественным будет звучание. Причем, чем больше будет количество измерений уровня звукового сигнала в единицу времени, тем качественнее будет звучание. Эта характеристика называется частотой дискретизации Данная характеристика измеряется в Гц.

При этом на каждое измерение выделяется одинаковое количество бит. Такая характеристика называется — глубина кодирования.

Таким образом, чтобы подсчитать вес звуковой волны достаточно перемножить частоту дискретизации, глубины кодирования и времени звучания такого звука. При этом, рассматривая современное звучание, количество звуковых волн может быть различное, например, для стереозвука — это 2, а для квадрозвука — 4.

Источник

Для кодирования какого вида информации требуется дискретизация

Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации

Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.

Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.

Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.

Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.

Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.

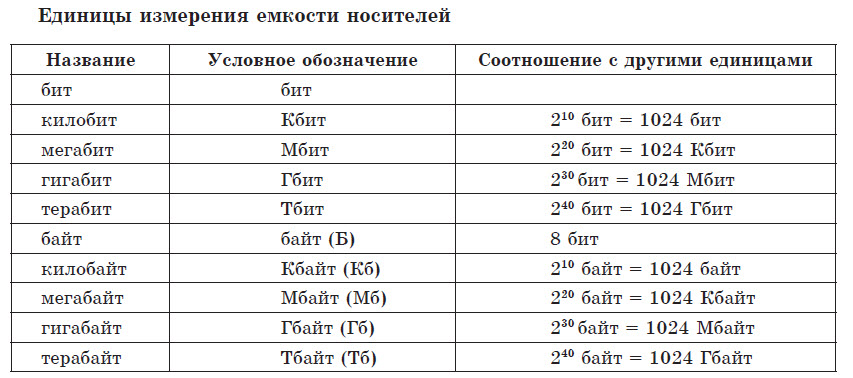
Единицы измерения количества информации

Основной единицей хранения и обработки цифровой информации принят байт.

Соответственно, с помощью одного байта можно получить 256 (= 2 8 ) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.

На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 2 10 ).

Системы счисления

Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.

Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.

Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.

Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.

В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.

Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.

В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.

Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.

Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.

Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.

348 = 3 • 10 2 + 4 • 10 1 + 8 • 10 0

–348,17 = –(3 • 10 2 + 4 • 10 1 + 8 • 10 0 + 1 • 10 –1 + 7 • 10 –2 )

Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:

316 — число в десятичной системе счисления,
316₈ — число в восьмеричной системе счисления.

Свойства записи чисел в позиционной системе счисления:

Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.

Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.

В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а₁, а₂, а₃ и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:

Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.

Представление числа в виде многочлена называют развернутой записью числа:

Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:

Конспект урока по информатике «Дискретная форма представления информации».

Источник

Информатика

План урока:

Примеры кодирования информации:

Другими словами, переход сообщения из одной формы ее в другую, согласно определенным правилам, и выражает в чем суть кодирования информации.

Информация проходит кодирование в целях:

История кодирования информации насчитывает сотни веков. Издавна люди использовали криптограммы (зашифрованные сообщения).

В 19 веке с изобретением телеграфа С. Морзе был придуман и принципиально новый способ шифрования. Телеграфное сообщение передавалось по проводам последовательностью коротких и долгих сигналов (точка и тире).

Вслед за ним Ж. Бодо создал основополагающий в истории современной информатики метод бинарного кодирования информации, который заключается в применении всего двух различающихся электрических сигналов. Кодирование информации в компьютере также подразумевает использование двух чисел.

Разработанная в 1948г. К. Шенноном «Теория информации и кодирования» стала основополагающей в современном кодировании данных.

Кодирование информации в информатике, одна из базовых тем. Понимание для чего нужна процедура кодирования передаваемой информации, каким образом она осуществляется, поможет в изучении принципов работы компьютера.

Способы кодировки

Проанализируем разнообразные виды информации и особенности ее кодирования.

По принципу представления все информационные сведения можно классифицировать на следующие группы:

Способы кодирования информации обусловлены поставленными целями, а также имеющимися возможностями,методами ее дальнейшей обработки и сохранения. Одинаковые сообщения могут отображаться в виде картинок и условных знаков (графический способ), чисел (числовой способ) или символов (символьный способ).

Соответственно происходит и классификация информации по способу кодирования:

Чтобы расшифровать сообщение, отображаемое в выбранной системе кодирования информации, необходимо осуществить декодирование – процесс восстановления до исходного материала. Для успешного осуществления расшифровки необходимо знать вид кода и методы шифрования.

Самыми распространенными видами кодировок информации являются следующие:

Различают такие методы кодирования информации как:

Двоичный код

Самый широко используемый метод кодирования информации – двоичное кодирование. Кодирование данных двоичным кодом применяется во всех современных технологиях.

Двоичное кодирование информации применяется для различных данных:

Обработка графических изображений

Кодирование текстовой, звуковой и графической информации осуществляется в целях ее качественного обмена, редактирования и хранения. Кодировка информационных сообщений различного типа обладает своими отличительными чертами, но, в целом, она сводится к преобразованию их в двоичном виде.

Рисунки, иллюстрации в книгах, схемы, чертежи и т.п. – примеры графических сообщений. Современные люди для работы с графическими данными все чаще применяют компьютерные технологии.

Суть кодирования графической и звуковой информации заключается в преобразовании ее из аналогового вида в цифровой.

Кодирование графической информации – это процедура присвоения каждому компоненту изображения определенного кодового значения.

Способы кодирования графической информации подчиняются методам представления изображений (растрового или векторного):

Источник

Многим станет интересно: «В чем суть кодирования графической информации, представленной в виде 3D-изображений?» Дело в том, что работа с трехмерными данными сочетает способы растровой и векторной кодировки.

Кодирование и обработка графической информации различного формата имеет как свои преимущества, так и недостатки.

Метод координат

Любые данные можно передать с помощью двоичных чисел, в том числе и графические изображение, представляющие собой совокупность точек. Чтобы установить соответствие чисел и точек в бинарном коде, используют метод координат.

Метод координат на плоскости основан на изучении свойств точки в системе координат с горизонтальной осью Ox и вертикальной осью Oy. Точка будет иметь 2 координаты.

Если через начало координат проходит 3 взаимно перпендикулярные оси X, Y и Z, то используется метод координат в пространстве. Положение точки в таком случае определяется тремя координатами.

Система координат в пространстве

Перевод чисел в бинарный код

Числовой способ кодирования информации, т.е. переход информационных данных в бинарную последовательность чисел широко распространен в современной компьютерной технике. Любая числовую, символьную, графическую, аудио- и видеоинформацию можно закодировать двоичными числами. Рассмотрим подробнее кодирование числовой информации.

Привычная человеку система счисления (основанная на цифрах от 0 до 9), которой мы активно пользуемся, появилась несколько сотен тысяч лет назад. Работа всей вычислительной техники организована на бинарной системе счисления. Алфавитом у нее минимальный – 0 и 1. Кодировка чисел совершается путем перехода из десятичной в двоичную систему счисления и выполнении вычислений непосредственно с бинарными числами.

Кодирование и обработка числовой информации обусловлено желаемым результатом работы с цифрами. Так, если число вводится в рамках текстового файла, то оно будет иметь код символа, взятого из используемого стандарта. Для математических вычислений числовые данные преобразуются совершенно другим способом.

Принципы кодирования числовой информации, представленной в виде целых или дробных чисел (положительных, отрицательных или равных 0) отличаются по своей сути. Самый простой способ перевести целое число из десятичной в двоичную систему счисления заключается в следующем:

Одна из важнейших частей компьютерной работы – кодирование символьной информации. Все многообразие цифр, русских и латинских букв, знаков препинания, математических знаков и отдельных специальных обозначений относятся к символам. Cимвольный способ кодирования состоит в присвоении определенному знаку установленного шифра.

Рассмотрим подробнее самые распространенные стандарты ASCII и Unicode – то, что применяется для кодирования символьной информации во всем мире.

Фрагмент таблицы ASCII

Первоначально было установлено, что для любого знака отводится в памяти компьютера 8 бит (1 бит – это либо «0», либо «1») бинарной последовательности. Первая таблица кодировки ASCII (переводится как «американский кодовый стандарт обмена сообщениями») содержала 256 символов. Ограниченная численность закодированных знаков, затрудняющая межнациональный обмен данными, привела к необходимости создания стандарта Unicode, основанного на ASCII. Эта международная система кодировки содержит 65536 символов. Закодировать огромное количество всевозможных обозначений стало возможным благодаря использованию 16-битного символьного кодирования.

Кодирование символьной и числовой информации принципиально отличается. Для ввода-вывода цифр на монитор или использовании их в текстовом файле происходит преобразование их согласно системе кодировки. В процессе арифметических действий число имеет совершенно другое бинарное значение, потому что оно переходит в двоичную систему счисления, где и совершаются все вычислительные действия.

Выбирать способ кодирования информации – графический, числовой или символьный необходимо отталкиваясь от цели кодировки. Например, число «21» можно ввести в компьютерную память цифрами или буквами «двадцать один», слово «ЗИМА» можно передать русскими буквами «зима» или латинскими «ZIMA», штрих-код товара передается изображением и цифрами.

Преобразование звука

Компьютерные технологии успешно внедряются в различные сферы деятельности, включая кодирование и обработку звуковой информации. С физической точки зрения, звук – это аналоговый сплошной сигнал. Процесс его перевода в ряд электрических импульсов называется кодированием звуковой информации.

Задачи, которые необходимо решить для успешной оцифровки сигнала:

Преобразование звука: а) аналоговый сигнал; б)дискретный сигнал.

Различают следующие методы кодирования звуковой информации:

Обработка текста

Текст – осмысленный порядок знаков. С использованием компьютера кодирование и обработка текстовой информации (набор, редактирование, обмен и сохранение письменного текста) значительно упростилось.

Кодирование текстовой информации – присвоение любому символу текста кода из кодировочной системы. Различают следующие стандарты кодировки:

В задачах на кодирование текстовой информации часто встречаются следующие понятия:

Например, мощность алфавита ASCII составляет 256 символов. При этом один знак занимает 8 бит (или 1 байт) памяти, а Unicode – 35536 символов и 16 бит (или 2 байта) соответственно.

Источник