двоичное кодирование арифметические основы построения эвм
2. Глобальные сети
Существует 7 основных путей использования INTERNET:
1. Электронная почта.
2. Отправка и получение файлов.
3. Чтение и посылка текстов..
4. Поиск информации
5. Удаленное управление.
6. Возможность разговаритьс многими людьми с помощью IRC.
7. Игры через INTERNET.
3.Топология локальных сетей
Существуют три основных вида топологий: «общая шина», «звезда» и «кольцо».
МЕТОДЫ ДОСТУПА И ПРОТОКОЛЫ ПЕРЕДАЧИ ДАННЫХ Наибольшее распространение получили конкретные реализации методов доступа: Ethernet, Arcnet и Token-Ring.
8) Двоичное кодирование. Арифметические основы построении компьютера.
В отличие от привычного для нас десятичного кодирования чисел, то есть кода с основанием десять, при двоичном кодировании в основании кода лежит число два., всего лишь два — 0 и 1. Система позиционной записи остается такой же, то есть справа пишется самый младший разряд, а слева — самый старший. Но если в десятичной системе вес каждого следующего разряда больше веса предыдущего в десять раз, то в двоичной системе (при двоичном кодировании) — в два раза. Каждый разряд двоичного кода называется бит.
Для того чтобы упростить запись двоичных чисел, была предложена так называемая шестнадцатиричная система. В этом случае все двоичные разряды разбиваются на группы по четыре разряда (начиная с младшего), а затем уже каждая группа кодируется одним символом. Каждая такая группа называется полубайтом (или нибблом, тетрадой ), а две группы (8 разрядов) — байтом В качестве первых 10 символов берутся цифры от 0 до 9, а затем используются 6 начальных заглавных букв латинского алфавита
Арифметические основы построении компьютера.
Перевод числа из одной системы счисление в другую.
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. Эта система имеет ряд преимуществ перед другими системами:
— для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
— представление информации посредством только двух состояний надежно и помехоустойчиво;
— возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
— двоичная арифметика намного проще десятичной.
Арифметические операции в позиционных системах счисления.
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление.
Умножение
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе.
9) Логические основы построения ком-ра, основные логич. операции, средства их реализации.
Логические основы компьютера.
В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.
Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.
Логические операции. Дизъюнкция, конъюнкция и отрицание:
1)конъюнкция (И), 2)дизъюнкция (ИЛИ) и 3)отрицание (НЕ). При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.
При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.
Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.
Средством обработки двоичных сигналов в компьютере являются логические элементы. Для реализации любых логических операций достаточно элементов трёх типов – элементов, реализующих три основные логические операции: И, ИЛИ, НЕ.
Арифметические основы построения ЭВМ
Системой счисления называется совокупность правил для обозначения (записи) действительных чисел с помощью цифровых знаков. Для записи чисел в конкретных системах счисления используется некоторый конечный алфавит, состоящий из цифр 

Непозиционные системы счисления
В ней количественный эквивалент каждой цифры, входящей в запись данного числа, не зависит от места (позиции) этой цифры в ряду других цифр. Пример: римская система счисления. В ней для записи различных целых чисел используются символы I, V, X, L, C, D, M и т.д., обозначающие соответственно 1, 5, 10, 50, 100, 500, 1000 и т.д. Например, запись MCMLXXXV означает число 1985. Общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа.
Позиционные системы счисления
Десятичная система счисления.
Двоичная система счисления.
Восьмеричная система счисления.
Шестнадцатеричная система счисления.
1. Арифметические основы построения эвм
Системой счисления называется совокупность правил для обозначения (записи) действительных чисел с помощью цифровых знаков. Для записи чисел в конкретных системах счисления используется некоторый конечный алфавит, состоящий из цифр 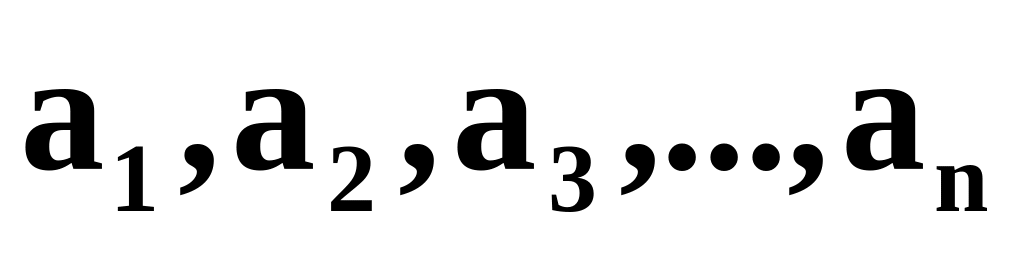

Непозиционные системы счисления
В ней количественный эквивалент каждой цифры, входящей в запись данного числа, не зависит от места (позиции) этой цифры в ряду других цифр. Пример: римская система счисления. В ней для записи различных целых чисел используются символы I, V, X, L, C, D, M и т.д., обозначающие соответственно 1, 5, 10, 50, 100, 500, 1000 и т.д. Например, запись MCMLXXXV означает число 1985. Общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа.
Позиционные системы счисления
Десятичная система счисления.
Двоичная система счисления.
Восьмеричная система счисления.
Шестнадцатеричная система счисления.
Правила перевода из системы счисления в систему счисления
Для перевода чисел из любой системы счисления в десятичную необходимо:
Старшую цифру исходного числа умножить на основание старой системы счисления и прибавить следующую цифру исходного числа.
Результат опять умножить на основание старой системы счисления и прибавить следующую цифру исходного числа.
Процесс перевода заканчивается после прибавления последней самой младшей цифры исходного числа.
Для перевода чисел из десятичной системы счисления в любую необходимо делить исходное число на основание новой системы счисления до тех пор пока последнее частное не станет меньше основания новой системы счисления. Результат складывается из остатков деления, начиная с последнего.
Для перевода чисел из любой системы счисления в любую необходимо исходное число перевести в десятичную систему по первому правилу (умножением), полученное десятичное число перевести в искомую систему по второму правилу (деление).
Представление чисел в различных системах счисления
Конспект лекций по Вычислительной технике, Раздел»Арифметические основы построения ЭВМ»
Новые аудиокурсы повышения квалификации для педагогов
Слушайте учебный материал в удобное для Вас время в любом месте
откроется в новом окне
Выдаем Удостоверение установленного образца:
Тема 2.1. Виды информации и способы представления ее в ЭВМ
Виды информации, обрабатываемые с помощью ЭВМ.
Числовая, текстовая, графическая, звуковая.
Способы представления информации: дискретная и аналоговая.
Представление информации физическими сигналами.
Кодирование информации с помощью потенциального и импульсного кода.
Последовательные и параллельные коды
Информация всегда связана с материальным носителем. Носитель информации – это среда для передачи и хранения информации. Носителем информации может быть любой материальный предмет (бумага, стена, камень, поверхность диска магнитного или лазерного), волны различной природы (акустическая – звук, электромагнитная – свет, радиоволна, гравитационная – давление, притяжение), особые состояния вещества (температура и давление газа, концентрация молекул в жидком растворе, расположение молекул в кристалле процессора).
Способ передачи информации – сигнал.
Информационный сигнал – физический процесс, имеющий для человека или технического устройства информационное значение.
Сигнал может быть непрерывным (аналоговым) или дискретным (цифровым).
Аналоговый сигнал – сигнал, непрерывно изменяющийся по амплитуде и во времени.
Дискретный сигнал может принимать лишь конечное число значений в определенные периоды времени.
В реальной жизни человек чаще всего воспринимает аналоговые сигналы. Например, речь человека представляет собой непрерывный сигнал. В этом легко убедиться, если вспомнить, что речь на незнакомом языке воспринимается слитно, в ней трудно выделить отдельные слова. Дискретные сигналы легче обрабатывать. Аналоговые сигналы всегда могут быть представлены в дискретном виде, в виде последовательности чисел. Процесс представления какой-либо величины в виде последовательного ряда ее отдельных (дискретных) значений называется дискретизацией.
Вычислительная техника может работать как с аналоговыми, так и с дискретными сигналами. Соответственно, существуют аналоговые вычислительные машины (АВМ) и цифровые вычислительные машины (ЦВМ), причем последние получили значительно большее распространение.
Информацию можно классифицировать по ее форме представления, способам ее кодирования и хранения:
• графическая или изобразительная — первый вид, для которого был реализован способ хранения информации об окружающем мире в виде наскальных рисунков, а позднее в виде картин, фотографий, схем, чертежей на бумаге, холсте, мраморе и др. материалах, изображающих картины реального мира;
• звуковая — мир вокруг нас полон звуков и задача их хранения и тиражирования была решена с изобретение звукозаписывающих устройств в 1877 г.); ее разновидностью является музыкальная информация — для этого вида был изобретен способ кодирования с использованием специальных символов, что делает возможным хранение ее аналогично графической информации;
• текстовая — способ кодирования речи человека специальными символами — буквами, причем разные народы имеют разные языки и используют различные наборы букв для отображения речи; особенно большое значение этот способ приобрел после изобретения бумаги и книгопечатания;
• числовая — количественная мера объектов и их свойств в окружающем мире; особенно большое значение приобрела с развитием торговли, экономики и денежного обмена; аналогично текстовой информации для ее отображения используется метод кодирования специальными символами — цифрами, причем системы кодирования (счисления) могут быть разными;
• видеоинформация — способ сохранения «живых» картин окружающего мира, появившийся с изобретением кино.
Существуют также виды информации, для которых до сих пор не изобретено способов их кодирования и хранения — это тактильная информация, передаваемая ощущениями, органолептическая, передаваемая запахами и вкусами и др.
Для передачи информации на большие расстояния первоначально использовались кодированные световые сигналы, с изобретением электричества — передача закодированного определенным образом сигнала по проводам, позднее — с использованием радиоволн.
Представление информации в ЭВМ
Любая информация представляется в ЭВМ в виде чисел и располагается в оперативной памяти, так происходит потому, что цифровую информацию очень удобно кодировать, а значит, ее удобно хранить и обрабатывать.
За единицу представления информации в ЭВМ принимают один бит (от binary digit). Бит может принимать значения 0 или 1.
Бит – очень маленькая единица информации, она удобна для хранения информации в компьютере, но неудобна для ее обработки.
Обработкой информации в компьютере занимается специальная микросхема – процессор, который может одновременно обрабатывать группу битов. Поэтому за единицу обработки или передачи информации принимается один байт, который представляет собой последовательность из восьми битов. Байты могут объединяться по два, четыре, восемь байтов и образовывать неполное стандартное, длинное слово (ячейка) соответственно. Каждая ячейка может содержать число или команду, записанных с помощью единиц и нулей. Способ представления чисел посредством числовых знаков (цифр) называют системой счисления (СС). Правила записи и действий над числами в СС, используемых в цифровой вычислительной технике, определяют арифметические основы цифровых ЭВМ.
Физическими аналогами логических переменных «0» и «1» служат сигналы, способные принимать два хорошо различимых состояния, например, потенциал низкого и высокого уровней, разомкнутое и замкнутое состояние контакта реле и т.п.
В цифровых вычислительных устройствах обычно применяют потенциальный и импульсный способы физического представления информации.
Рис. 2.1. Способы представления цифровой информации:
При потенциальном способе (рис 2.1, а) двум значениям переменной 1 и 0 соответствуют разные уровни напряжения в соответствующей точке схемы машины (потенциальный код ). Потенциальный сигнал сохраняет постоянный уровень в течение такта, а его значение в переходные моменты не является определенным.
При импульсном способе представления информации (рис. 2.1,б) единичное и нулевое значения двоичной переменной отображаются наличием и отсутствием электрического импульса.
В соответствии с типом используемых сигналов для представления информации схемы цифровых устройств принято делить на импульсные, потенциальные и импульсно-потенциальные.
В современных ЦУ применяется потенциальный способ представления информации. Потенциальный сигнал сохраняет постоянный уровень в течение такта, а его значение в переходные моменты не является определенным
Машинное слово может быть представлено последовательным или параллельным кодом.
При последовательном коде каждый временной такт предназначен для отображения одного разряда кода слова (рис. 2.2). В этом случае все разряды слова фиксируются по очереди одним и тем же элементом и проходят через одну линию передачи информации.
При параллельном коде все разряды двоичного кода слова представляются в одном временном такте, фиксируются отдельными элементами и проходят через отдельные линии, каждая из которых служит для представления и передачи только одного разряда слова.
При параллельной передаче информации код слова развертывается не во времени, а в пространстве, так как значения всех разрядов слова передаются по нескольким линиям одновременно (рис. 2.3).

Р
Рис. 2.3. Параллельный импульсный код (а) и параллельный потенциальный код (б)
В зависимости от применяемого кода устройства вычислительной техники называются последовательными или параллельными. При использовании последовательного кода все операции, в том числе передача слов из одного узла в другой, производятся поочередно для каждого разряда слова, и поэтому последовательные устройства работают медленнее, чем параллельные.
В современных ЭВМ основные устройства, участвующие в обработке информации, для достижения высокого быстродействия строятся как параллельные, хотя они и требуют большего объема аппаратуры. Для экономии оборудования в некоторых устройствах применяют последовательно-параллельный код, при котором слова разбиваются на части (слоги) и передача, а иногда и обработка производятся последовательно слог за слогом. При этом каждый слог представляется параллельным кодом.
Тема 2.1. Виды информации и способы представления ее в ЭВМ
Позиционные системы счисления, применяемые в цифровой технике.
В заимосвязь между системами счисления.
Преимущества и недостатки различных систем счисления.
Келим Ю.М. Вычислительная техника, стр. 76 – 78
Современные вычислительные машины оперируют с информацией, пред- ставленной в цифровой форме. Числовые данные преобразуются в двоичную си- стему счисления, а в качестве промежуточных систем счисления используются восьмеричная и шестнадцатеричная.
Система счисления – это совокупность приёмов и правил изображения чисел цифровыми знаками. Системы счисления делятся на непозиционные и позиционные.
Основным недостатком такой системы является большое число различных знаков и сложность выполнения арифметических операций.
Позиционная система счисления – это система, в которой значение символа зависит от его места (позиции) в ряду цифр, изображающих число. Например, в числе 548 первая цифра означает количество сотен, вторая – десятков, третья – единиц. Позиционные системы счисления более удобны для вычислительных операций, поэтому они получили наибольшее распространение.
Основание (или базис) позиционной системы счисления – это количество знаков или символов, используемых для изображения числа в разрядах данной системы счисления.
При написании числа система счисления обозначается индексом, проставленным справа внизу у числа и представляющим собой основание соответствующей с/с, записанное в десятичной системе. Так, записи некоторых чисел в двоичной, восьмеричной и шестнадцатеричной системах счисления выглядят следующим образом: 11011,01 2 ; 431,67 8 ; А28Е,С4 16
В позиционных системах счисления используется принцип умножения и сложения. В таких системах с основанием q произвольное число
записывается в общем виде:
Главным преимуществом позиционных систем счисления по сравнению с непозиционными является удобство представления чисел и простота выполнения арифметических действий.
Одно и то же число можно представить в различных системах счисления. Запись числа при этом различна, а значение остается неизменным.
Позиционные системы счисления, применяемые в цифровой технике
Для физического представления чисел необходимы элементы, способные находиться в одном из нескольких устойчивых состояний. Число этих состояний должно быть равно основанию принятой системы счисления. Тогда каждое состояние будет представлять соответствующую цифру из алфавита данной системы счисления.
Если при записи чисел в ЭВМ мы хотим использовать десятичную систему счисления, то мы должны получить 10 устойчивых состояний для каждого разряда (как на счетах при помощи косточек). Конструкция элементов такой машины оказывается чрезвычайно сложной, что сказывается на надежности и скорости ЭВМ.
Наиболее надежным и дешевым является устройство, каждый разряд которого может принимать два состояния: намагничено – не намагничено, высокое напряжение – низкое напряжение. В современной электронике развитие аппаратной базы ЭВМ идет именно в этом направлении. Следовательно, использование двоичной системы в качестве внутренней системы представления информации вызвано конструктивными особенностями ЭВМ.
Двоичная, восьмеричная и шестнадцатеричная системы счисления относятся к так называемой «машинной группе». Каждая система счисления из этой группы применяется в различных случаях, а именно:
двоичная – используется для организации преобразования информации, кодирования дискретного сигнала, потребителем которого является вычислительная техника, поскольку двоичный сигнал проще реализовать на аппаратном уровне;
восьмеричная и шестнадцатеричная – используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.
десятичная система применяется в ЭВМ для ввода данных и вывода на устройства печати и на экран дисплея.
Двоичная система счисления – основание q =2. Для записи числа используются две цифры: 0 и 1. При этом каждый старший разряд больше соседнего младшего в два раза. Любое число в двоичной системе счисления представляется в виде суммы целых степеней основания q =2, умноженных на соответствующие коэффициенты (0 или 1). Например, двоичное число 1001,1001 2 представляет собой сокращенную запись выражения:
Восьмеричная система счисления – основание q =8. Используются цифры: 0, 1, 2, …, 7. Любое число представляется суммой целых степеней основания q =8, умноженных на соответствующие коэффициенты a i =0, …, 7. Например, восьмеричное число 4517,621 8 представляет собой сокращенную запись выражения:
Шестнадцатеричная система счисления – основание q =16. Алфавит цифровых знаков состоит из 16-ти символов: первые десять – арабские цифры от 0 до 9 и дополнительные – A(10), B(11), C(12), D(13), E(14), F(15).
Например, шестнадцатеричное число 1AE,4C 16 представляет собой сокращенную запись выражения:
Пример: Записать в виде многочлена числа 789,35 10 ; 1101,0101 2 ; 3,4 16 ; 657,341 8
Для преобразования числа из недесятичной позиционной системы счисления в десятичную форму необходимо записать число в виде многочлена ( I ) и произвести его вычисление, пользуясь десятичной арифметикой. При этом для системы счисления, где цифры представляются буквами, последние при вычислении заменяются на десятичные эквиваленты, например: А=10, В=11, С=12, D =13, Е =14, F =15.
Тема 2.2. Перевод чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую.
Правила перевода целой и дробной части.
Келим Ю.М. Вычислительная техника, стр. 78 – 81
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Пример 1 . Переведем число 159 из десятичной СС в двоичную СС:

