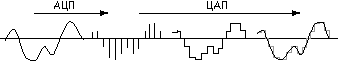двоичное кодирование примеры легкие
Двоичное кодирование
Урок 17. Информатика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Двоичное кодирование»
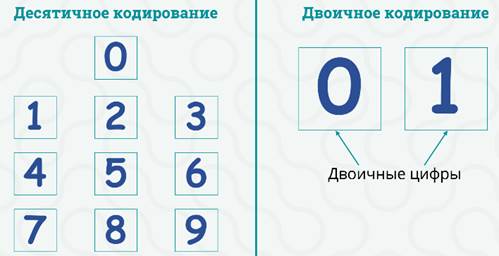
Привет, мальчишки и девчонки. Вы, наверное, уже обратили внимание, что на доске у меня написаны две цифры: ноль и один. Именно они используются в двоичном кодировании.
Сегодня вы будете учиться кодировать числовую информацию с помощью нулей и единиц; отличать двоичное кодирование от десятичного. Не спешите, ребята. Про это мы тоже поговорим. А пока я предлагаю вспомнить, что такое десятичное кодирование.
Вы уже знаете, что числовая информация, которая закодирована с помощью чисел, – это числовые данные.
Десятичное кодирование – это кодирование числа десятью знаками (цифрами) от нуля до девяти. А получившееся в результате этого число называется десятичным числом. Любое количество предметов и их порядковые номера можно представить десятичным числом, то есть с помощью всего лишь десяти цифр.
Даже если, как для числа четыреста тридцать четыре, мы использовали всего две цифры: четыре и три, это десятичное кодирование, а не двоичное.
Можно использовать и другие знаки. Букву А заменить, например, нулём, а букву Бэ заменить единицей.
Значит, двоичное кодирование – это кодирование информации с помощью двух знаков.
Чтобы сохранить информацию в памяти компьютера, её кодируют с помощью двух конкретных знаков – цифр ноль и один. Этот способ кодирования связан с устройством компьютерной памяти.
Компьютер не понимает смысла данных, которые находятся в его памяти. Он может работать только с электрическими сигналами и различает два состояния: «есть сигнал» и «нет сигнала». Если сигнала нет, то при описании данных для компьютера это состояние обозначают нулём. Если сигнал есть, то при описании данных для компьютера это состояние обозначают единицей. Ноль – нет сигнала. Единица – есть сигнал. Запомнили.
Как мы уже знаем, при десятичном кодировании для представления числа используют десять цифр. А при двоичном кодировании только две: ноль и один. Их называют двоичными цифрами. А число, которое составлено при помощи только двух знаков, называют двоичным числом.
Числом из двух знаков (цифр) можно закодировать любое количество предметов и любой порядковый номер предмета. Как и у десятичных цифр, так и у каждой двоичной цифры есть своё значение.
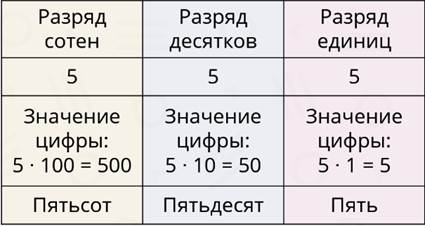
Помните, при кодировании числа с помощью десяти цифр значение каждой цифры в числе зависит от её положения в числе.
Например, в данном случае, цифра пять в разряде единиц имеет значение «пять единиц» – пять. В разряде десятков цифра пять имеет значение «пять десятков» – «пятьдесят». А в разряде сотен пятёрка имеет значение «пять сотен» – пятьсот.
Как и при десятичном кодировании, в двоичном кодировании значение цифры один изменяется в зависимости от её положения в числе. Оно определяется разрядом числа, то есть местом, которое эта цифра занимает в числе. А вот цифра ноль всегда имеет одно и то же значение – «ноль», какое бы место в числе ноль не занимал. Более подробно об этом вы узнаете в старших классах.
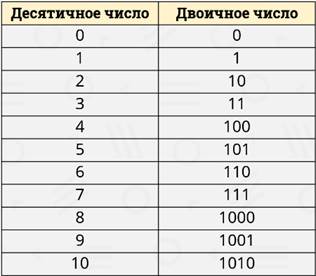
А сейчас давайте посмотрим вот такую таблицу.
Слева записано десятичное число, а справа двоичное число, которое обозначает то же самое количество, что и десятичное число.
Можно, конечно, просто запомнить, как выглядет перевод этих одиннадцати чисел из десятичной системы с двоичную. Это хорошо тренирует память.
Кстати, обратите, внимание, что если десятичное число чётное, то двоичное число оканчивается нулём, а если десятичное число нечётное, то двоичное число оканчивается единицей. Всё просто.
А сейчас я вам покажу способ, который поможет вам перевести любое десятичное число в двоичное. Это деление пополам, то есть на две равные части. Давайте сразу рассмотрим на примере, чтобы было всё наглядно и понятно. Предлагаю перевести десятичное число восемь в двоичное число.
Делим восемь пополам. Получается две четвёрки. Записываем одно число четыре. А в двоичное число записываем ноль. Ведь мы число восемь поделили на две равные части и ничего лишнего не осталось. Далее число четыре тоже делим на две равные части. Получается две двойки. Одну записываем, а в двоичное число опять пишем ноль. Ведь вы, надеюсь, поняли, что ноль мы пишем, если число можно разделить на две равные части. Продолжаем делить пополам. Два делим на две равные части – будет по единице. Единицу записываем, а в двоичном числе снова ноль. Один напополам уже разделить нельзя. Поэтому его просто записываем в двоичном числе. Вот тут важный момент. Записывать полученные цифры для двоичного числа надо в обратном порядке. Один, ноль, ноль, ноль. Вот так выглядит число восемь, если его записывать в двоичной системе.
Сверяем с нашей уже заполненной таблицей. Да, всё верно.
Теперь давайте переведём десятичное число девять в двоичное число. Делим девять пополам. «Ой!», подумали вы, «нельзя девять разделить на две равные части». Верно. Поэтому мы единичку запишем в двоичное число, как бы отнимем её от девятки. Получилось восемь. Вот восьмёрку теперь легко разлелить пополам. Будет четыре. В двоичное число записываем ноль. Число четыре делим на две равные части, получается две двойки. Одну записываем, а в двоичное число пишем ноль. Продолжаем делить пополам. Два делим на две равные части – будет по единице. Единицу записываем, а в двоичном числе снова ноль. Один напополам не делится. Поэтому его просто записываем в двоичном числе. Получается, что десятичное число девять в виде двоичного числа выглядит так: один, ноль, ноль, один. Получилось, как в таблице.
Ну и давайте переведём ещё одно число, не из нашей таблицы. Например, пятнадцать. На две равные части не делится. Значит мы как бы отнимаем единичку и записываем её в двоичное число, а пополам делим число четырнадцать. Получается семь. Семь снова не делится пополам. Значит из семи опять вычитаем единичку и записываем её в двоичное число, а пополам делим число шесть. Получается три. И три поплам не делится. Снова вычитаем из трёх и записываем единичку, а делим число два. Два делим на две равные части – будет по единице. Один напополам никак не разделить. Просто записываем его в двоичном числе. Не забываем, двоичное число пишем в обратном порядке: один, один, один, один. Даже в таких случаях. Ведь нужно вырабатывать у себя хорошую привычку делать всё правильно.
Думаю, что если потренировать ещё на нескольких числах, то всё у вас будет получаться легко. Тут, конечно, важно, умень хорошо считать. Так что наука математика точно пригодится.
Ну вот и всё на сегодня. Осталось только, как всегда, заполнить наш словарь.
Двоичные цифры – это цифры, которые используются в двоичном кодировании (ноль и один).
Двоичное число – число, которое составлено только из двух знаков.
Двоичное кодирование – это кодирование информации при помощи двух знаков.
У двоичного числа по сравнению с десятичным есть недостаток. Для обозначения того же самого количество в двоичном числе используется большее число разрядов. Например, десятичное число девять представлено четырьмя двоичными цифрами. А число сто – семью двоичными цифрами! Ну, ничего не поделаешь, такая система.
Вот и подошла пора прощаться. До свидания, мальчики и девочки! До новых встреч!
Информатика
План урока:
Примеры кодирования информации:
Другими словами, переход сообщения из одной формы ее в другую, согласно определенным правилам, и выражает в чем суть кодирования информации.
Информация проходит кодирование в целях:
История кодирования информации насчитывает сотни веков. Издавна люди использовали криптограммы (зашифрованные сообщения).
В 19 веке с изобретением телеграфа С. Морзе был придуман и принципиально новый способ шифрования. Телеграфное сообщение передавалось по проводам последовательностью коротких и долгих сигналов (точка и тире).
Вслед за ним Ж. Бодо создал основополагающий в истории современной информатики метод бинарного кодирования информации, который заключается в применении всего двух различающихся электрических сигналов. Кодирование информации в компьютере также подразумевает использование двух чисел.
Разработанная в 1948г. К. Шенноном «Теория информации и кодирования» стала основополагающей в современном кодировании данных.
Кодирование информации в информатике, одна из базовых тем. Понимание для чего нужна процедура кодирования передаваемой информации, каким образом она осуществляется, поможет в изучении принципов работы компьютера.
Способы кодировки
Проанализируем разнообразные виды информации и особенности ее кодирования.
По принципу представления все информационные сведения можно классифицировать на следующие группы:
Способы кодирования информации обусловлены поставленными целями, а также имеющимися возможностями,методами ее дальнейшей обработки и сохранения. Одинаковые сообщения могут отображаться в виде картинок и условных знаков (графический способ), чисел (числовой способ) или символов (символьный способ).
Соответственно происходит и классификация информации по способу кодирования:
Чтобы расшифровать сообщение, отображаемое в выбранной системе кодирования информации, необходимо осуществить декодирование – процесс восстановления до исходного материала. Для успешного осуществления расшифровки необходимо знать вид кода и методы шифрования.
Самыми распространенными видами кодировок информации являются следующие:
Различают такие методы кодирования информации как:
Двоичный код
Самый широко используемый метод кодирования информации – двоичное кодирование. Кодирование данных двоичным кодом применяется во всех современных технологиях.
Двоичное кодирование информации применяется для различных данных:
Обработка графических изображений
Кодирование текстовой, звуковой и графической информации осуществляется в целях ее качественного обмена, редактирования и хранения. Кодировка информационных сообщений различного типа обладает своими отличительными чертами, но, в целом, она сводится к преобразованию их в двоичном виде.
Рисунки, иллюстрации в книгах, схемы, чертежи и т.п. – примеры графических сообщений. Современные люди для работы с графическими данными все чаще применяют компьютерные технологии.
Суть кодирования графической и звуковой информации заключается в преобразовании ее из аналогового вида в цифровой.
Кодирование графической информации – это процедура присвоения каждому компоненту изображения определенного кодового значения.
Способы кодирования графической информации подчиняются методам представления изображений (растрового или векторного):
Источник
Многим станет интересно: «В чем суть кодирования графической информации, представленной в виде 3D-изображений?» Дело в том, что работа с трехмерными данными сочетает способы растровой и векторной кодировки.
Кодирование и обработка графической информации различного формата имеет как свои преимущества, так и недостатки.
Метод координат
Любые данные можно передать с помощью двоичных чисел, в том числе и графические изображение, представляющие собой совокупность точек. Чтобы установить соответствие чисел и точек в бинарном коде, используют метод координат.
Метод координат на плоскости основан на изучении свойств точки в системе координат с горизонтальной осью Ox и вертикальной осью Oy. Точка будет иметь 2 координаты.
Если через начало координат проходит 3 взаимно перпендикулярные оси X, Y и Z, то используется метод координат в пространстве. Положение точки в таком случае определяется тремя координатами.
Система координат в пространстве
Перевод чисел в бинарный код
Числовой способ кодирования информации, т.е. переход информационных данных в бинарную последовательность чисел широко распространен в современной компьютерной технике. Любая числовую, символьную, графическую, аудио- и видеоинформацию можно закодировать двоичными числами. Рассмотрим подробнее кодирование числовой информации.
Привычная человеку система счисления (основанная на цифрах от 0 до 9), которой мы активно пользуемся, появилась несколько сотен тысяч лет назад. Работа всей вычислительной техники организована на бинарной системе счисления. Алфавитом у нее минимальный – 0 и 1. Кодировка чисел совершается путем перехода из десятичной в двоичную систему счисления и выполнении вычислений непосредственно с бинарными числами.
Кодирование и обработка числовой информации обусловлено желаемым результатом работы с цифрами. Так, если число вводится в рамках текстового файла, то оно будет иметь код символа, взятого из используемого стандарта. Для математических вычислений числовые данные преобразуются совершенно другим способом.
Принципы кодирования числовой информации, представленной в виде целых или дробных чисел (положительных, отрицательных или равных 0) отличаются по своей сути. Самый простой способ перевести целое число из десятичной в двоичную систему счисления заключается в следующем:
Одна из важнейших частей компьютерной работы – кодирование символьной информации. Все многообразие цифр, русских и латинских букв, знаков препинания, математических знаков и отдельных специальных обозначений относятся к символам. Cимвольный способ кодирования состоит в присвоении определенному знаку установленного шифра.
Рассмотрим подробнее самые распространенные стандарты ASCII и Unicode – то, что применяется для кодирования символьной информации во всем мире.
Фрагмент таблицы ASCII
Первоначально было установлено, что для любого знака отводится в памяти компьютера 8 бит (1 бит – это либо «0», либо «1») бинарной последовательности. Первая таблица кодировки ASCII (переводится как «американский кодовый стандарт обмена сообщениями») содержала 256 символов. Ограниченная численность закодированных знаков, затрудняющая межнациональный обмен данными, привела к необходимости создания стандарта Unicode, основанного на ASCII. Эта международная система кодировки содержит 65536 символов. Закодировать огромное количество всевозможных обозначений стало возможным благодаря использованию 16-битного символьного кодирования.
Кодирование символьной и числовой информации принципиально отличается. Для ввода-вывода цифр на монитор или использовании их в текстовом файле происходит преобразование их согласно системе кодировки. В процессе арифметических действий число имеет совершенно другое бинарное значение, потому что оно переходит в двоичную систему счисления, где и совершаются все вычислительные действия.
Выбирать способ кодирования информации – графический, числовой или символьный необходимо отталкиваясь от цели кодировки. Например, число «21» можно ввести в компьютерную память цифрами или буквами «двадцать один», слово «ЗИМА» можно передать русскими буквами «зима» или латинскими «ZIMA», штрих-код товара передается изображением и цифрами.
Преобразование звука
Компьютерные технологии успешно внедряются в различные сферы деятельности, включая кодирование и обработку звуковой информации. С физической точки зрения, звук – это аналоговый сплошной сигнал. Процесс его перевода в ряд электрических импульсов называется кодированием звуковой информации.
Задачи, которые необходимо решить для успешной оцифровки сигнала:
Преобразование звука: а) аналоговый сигнал; б)дискретный сигнал.
Различают следующие методы кодирования звуковой информации:
Обработка текста
Текст – осмысленный порядок знаков. С использованием компьютера кодирование и обработка текстовой информации (набор, редактирование, обмен и сохранение письменного текста) значительно упростилось.
Кодирование текстовой информации – присвоение любому символу текста кода из кодировочной системы. Различают следующие стандарты кодировки:
В задачах на кодирование текстовой информации часто встречаются следующие понятия:
Например, мощность алфавита ASCII составляет 256 символов. При этом один знак занимает 8 бит (или 1 байт) памяти, а Unicode – 35536 символов и 16 бит (или 2 байта) соответственно.
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Основы информатики
Примеры двоичного кодирования информации
Среди всего разнообразия информации, обрабатываемой на компьютере, значительную часть составляют числовая, текстовая, графическая и аудиоинформация. Познакомимся с некоторыми способами кодирования этих типов информации в ЭВМ.
Кодирование чисел
Существуют два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, второй (так называемое представление числа в формате с плавающей точкой) используется для задания некоторого подмножества действительных чисел.
Множество целых чисел, представимых в памяти ЭВМ, ограничено. Диапазон значений зависит от размера области памяти, используемой для размещения чисел. В k-разрядной ячейке может храниться 2 k различных значений целых чисел.
Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k-разрядном машинном слове, необходимо:
Пример. Получить внутреннее представление целого числа 1607 в 2-х байтовой ячейке.
Переведем число в двоичную систему: 160710 = 110010001112. Внутреннее представление этого числа в ячейке будет следующим: 0000 0110 0100 0111.
Для записи внутреннего представления целого отрицательного числа (-N) необходимо:
Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:
Кодирование текста
Множество символов, используемых при записи текста, называется алфавитом. Количество символов в алфавите называется его мощностью.
Для представления текстовой информации в компьютере чаще всего используется алфавит мощностью 256 символов. Один символ из такого алфавита несет 8 бит информации, т. к. 2 8 = 256. Но 8 бит составляют один байт, следовательно, двоичный код каждого символа занимает 1 байт памяти ЭВМ.
Для разных типов ЭВМ и операционных систем используются различные таблицы кодировки, отличающиеся порядком размещения символов алфавита в кодовой таблице. Международным стандартом на персональных компьютерах является уже упоминавшаяся таблица кодировки ASCII.
Принцип последовательного кодирования алфавита заключается в том, что в кодовой таблице ASCII латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений.
Стандартными в этой таблице являются только первые 128 символов, т. е. символы с номерами от нуля (двоичный код 00000000) до 127 (01111111). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, начиная со 128 (двоичный код 10000000) и кончая 255 (11111111), используются для кодировки букв национальных алфавитов, символов псевдографики и научных символов. О кодировании символов русского алфавита рассказывается в главе «Обработка документов».
Кодирование графической информации
Растровые изображения представляют собой однослойную сетку точек, называемых пикселами (pixel, от англ. picture element ). Код пиксела содержит информацию о его цвете.
| R | G | B | цвет |
|---|---|---|---|
| 0 | 0 | 0 | черный |
| 0 | 0 | 1 | синий |
| 0 | 1 | 0 | зеленый |
| 0 | 1 | 1 | голубой |
| R | G | B | цвет |
|---|---|---|---|
| 1 | 0 | 0 | красный |
| 1 | 0 | 1 | розовый |
| 1 | 1 | 0 | коричневый |
| 1 | 1 | 1 | белый |
Объекты векторного изображения, в отличии от растровой графики, могут изменять свои размеры без потери качества (при увеличении растрового изображения увеличивается зернистость). Подробнее о графических форматах рассказывается в разделе «Графика на компьютере».
Кодирование звука
Чем выше частота дискретизации (т. е. количество отсчетов за секунду) и чем больше разрядов отводится для каждого отсчета, тем точнее будет представлен звук. Но при этом увеличивается и размер звукового файла. Поэтому в зависимости от характера звука, требований, предъявляемых к его качеству и объему занимаемой памяти, выбирают некоторые компромиссные значения.
Описанный способ кодирования звуковой информации достаточно универсален, он позволяет представить любой звук и преобразовывать его самыми разными способами. Но бывают случаи, когда выгодней действовать по-иному.
Заметим, что существуют и другие, чисто компьютерные, форматы записи музыки. Среди них следует отметить формат MP3, позволяющий с очень большим качеством и степенью сжатия кодировать музыку. При этом вместо 18-20 музыкальных композиций на стандартный компакт-диск (CDROM) помещается около 200. Одна песня занимает примерно 3,5 Mb, что позволяет пользователям сети Интернет легко обмениваться музыкальными композициями.