двоичное восьмеричное и шестнадцатеричное кодирование данных в компьютерных системах
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Вы будете перенаправлены на Автор24
Данные системы счисления относятся к позиционным.
Двоичная система счисления
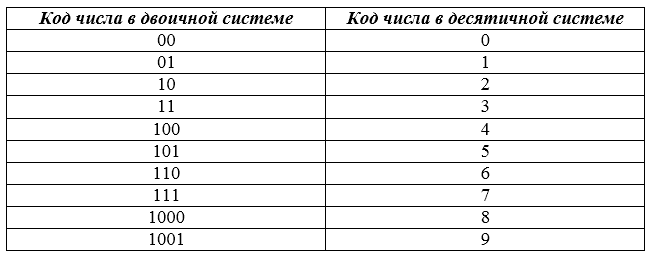
Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.
Готовые работы на аналогичную тему
Другой единицей измерения информации является байт.
Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.
Восьмеричная система счисления
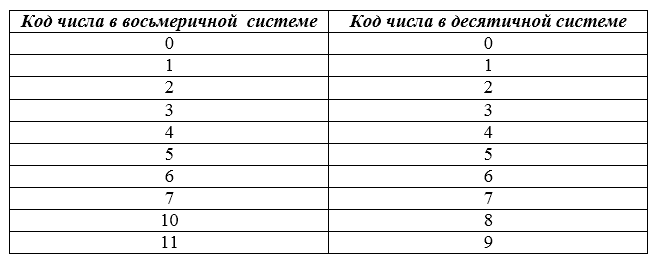
В таблице приведены соответствия чисел в восьмеричной и десятичной системах.
В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.
Шестнадцатеричная система счисления
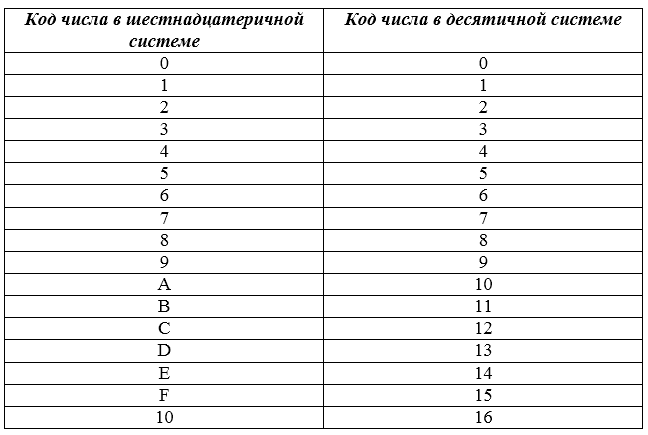
В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.
Перевод чисел из одной системы счисления в другую. Формы записи (кодирования) данных в эвм
Арифметические действия над целыми и вещественными числами
а) изучить и освоить алгоритмы перевода чисел из одной системы счислении в другую
б) изучить формы записи (кодирования) данных в ЭВМ с фиксированной точкой; получить практические навыки по выполнения арифметических операций с целими числами.
в) изучить формы записи (кодирования) данных в ЭВМ с плавающей точкой; получить практические навыки по выполнения арифметических операций с вещественными числами.
1. Перевод десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления
2. Перевод двоичных, восьмеричных и шестнадцатеричных чисел в десятичную систему счисления
3. Перевод восьмеричных и шестнадцатеричных чисел в двоичные
4. Перевод двоичных чисел в восьмеричную и шестнадцатеричную системы счисления
5.1. Представление целых чисел без знака
5.2. Представление целых чисел со знаком
6. Арифметические действия над целыми числами.
6.1 Арифметические операции в двоичной системе счисления.
6.2. Сложение и вычитание целых чисел со знаком в ЭВМ.
7.1. Форматы представления вещественных чисел.
7.2. Нормализованное представление вещественных чисел
8. Арифметические действия над вещественными числами.
8.1 Сложение и вычитание вещественных чисел.
8.2. Умножение и деление вещественных чисел.
Литература
1. Информатика: Учебник / Под ред. проф. Н.В.Макаровой. – М.: Финансы и статистика, 2001.
2. Информатика: Базовый курс / С.В.Симонович и др. – СПб.: Питер, 2002.
1. Перевод десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления Перевод чисел из одной системы счисления в другую
Пусть необходимо перевести число N(p), заданное в системе счисления с основанием р, в его представление N(q) в системе счисления с основанием q.
Существуют общие правила перевода:
для перевода целой части числа используется правило последовательного деления;
для перевода дробной части используется правило последовательного умножения.
Правило перевода целой части — правило последовательного деления:
Для перевода целой части числа N(p) с основанием р в целое число N(q) с основанием q необходимо последовательно делить целую часть числа N(p) и получаемые частные на основание новой системы счисления q, представленное в системе счисления р, до тех пор пока частное не станет меньше q. 2. Старшей цифрой записи числа N(q) служит последнее частное, а следующие за ней цифры являются остатками от деления частичных частных, записанными в порядке обратном их получения.
Правило перевода дробной части — правило последовательного умножения:
Для перевода дробной части числа N(p) с основанием р в дробное число N(q) с основанием q необходимо последовательно умножать исходную дробную часть числа N(p) и получаемые частные дробные части произведений на основание новой системы счисления q, представленное в системе счисления р. Количество умножений определяется заданной точностью. Целые части получающихся произведений дают последовательность цифр представления дроби в системе счисления с основанием q.
Разобрать пример преобразования в указанные системы счисления числа 142.378(10). Обратить внимание, что отдельно преобразуется целая часть числа, используя правило последовательного деления, и отдельно преобразуется дробная часть числа, используя правило последовательного умножения.
Преобразование целой части числа 142(10) в двоичное, восьмеричное и шестнадцатеричное числа:
Двоичная восьмеричная шестнадцатеричная системы счисления
Двоичная система счисления
где ai — двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
Например, число 17510 в шестнадцатеричной системе счисления запишется как AF16. Действительно,
10·16 1 +15·16 0 =160+15=175
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Три разряда двоичной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Пример: Преобразовать число 1101110,012 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
Четыре разряда двоичной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,112 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом:
Двоичное восьмеричное и шестнадцатеричное кодирование данных в компьютерных системах
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.
Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятк ов, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).
Позиционные системы счисления
Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.
Двоичное восьмеричное и шестнадцатеричное кодирование данных в компьютерных системах
Электронные облака
Лекции
Рабочие материалы
Тесты по темам
Template tips
Задачи
Логика вычислительной техники и программирования
Лекция «Системы счисления»
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Символы, при помощи которых записывается число, называются цифрами.
В конце концов, самой популярной системой счисления оказалась десятичная система. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э. В ней всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию несет не только цифра, но также и место позиция, на которой она стоит. В числе 444 три одинаковых цифры обозначают количество и единиц, и десятков, и сотен. А вот в числе 400 первая цифра обозначает число сотен, два 0 сами по себе вклад в число не дают, а нужны лишь для указания позиции цифры 4.
Классификация систем счисления
Системы счисления подразделяются на позиционные и непозиционные.
Позиционные системы счисления
Путем долгого развития человечество пришло к созданию позиционного принципа записи чисел, который состоит в том, что каждая цифра, содержащаяся в записи числа, занимает определенное место, называемое разрядом. Отсчет разрядов производится справа налево. Единица каждого следующего разряда всегда превосходит единицу предыдущего разряда в определенное число раз. Это отношение носит название основание системы счисления (у непозиционных систем счисления понятия «разряда» и «основания» отсутствуют).
Общее свойство всех позиционных систем счисления: при каждом переходе влево (вправо) в записи числа на один разряд величина цифры увеличивается (уменьшается) во столько раз, чему равно основание системы счисления.
Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. Например: Римская система счисления.
Из многочисленных представителей этой группы в настоящее время сохранила свое значение лишь римская система счисления, где для обозначения цифр используются латинские буквы:
| I | V | X | L | С | D | М |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
С их помощью можно записывать натуральные числа. Например, число 1995 будет представлено, как MCMXCV (М-1000,СМ-900,ХС-90 и V-5).
Правила записи чисел в римской системе счисления:
Например, запись XXX обозначает число 30, состоящее из трех цифр X, каждая из которых, независимо от места ее положения в записи числа, равна 10. Запись MCXX1V обозначает 1124, а самое большое число, которое можно записать в этой системе счисления, это число MMMCMXCIX (3999). Для записи еще больших чисел пришлось бы вводить все новые обозначения. По этой причине, а также по причине отсутствия цифры ноль, римская система счисления не годится для записи действительных чисел.
Таким образом, можно констатировать следующие основные недостатки непозиционных систем счисления:
Алфавит и основание системы счисления
Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например:
Десятичная система: <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>
Двоичная система: <0, 1>
Восьмеричная система: <0, 1, 2, 3, 4, 5, 6, 7>
Шестнадцатеричная система:
Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.
Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля.
Развёрнутая форма представления числа
Системы счисления, используемые в вычислительной технике
Несмотря на то, что исторически человек привык работать в десятичной системе счисления, с технической точки зрения она крайне неудобна, так как в электрических цепях компьютера требовалось бы иметь одновременно десять различных сигналов. Тем не менее, такие схемы существуют в некоторых видах микрокалькуляторов.
Чем меньше различных сигналов в электрических цепях, тем проще микросхемы, являющиеся основой конструкции большинства узлов ЭВМ, и тем надежнее они работают.
Наименьшее основание, которое может быть у позиционных систем счисления это – двойка. Именно поэтому двоичная система счисления используется в вычислительной технике, а двоичные наборы приняты за средство кодирования информации. В компьютере имеются только два устойчивых состояния работы микросхем, связанных с прохождением электрического тока через данное устройство (1) или его отсутствием (0). Говоря точнее, (1) кодирует высокое напряжение в схеме компьютера, а (0) – низкое напряжение.
Если вспомнить, что двоичная система счисления обладает самыми маленькими размерами таблиц сложения и умножения, то можно догадаться, что этот факт должен сильно радовать конструкторов ЭВМ, поскольку обработка сигнала в этом случае будет также самой простой. Таким образом, двоичная система счисления, с точки зрения организации работы ЭВМ, является наилучшей.
Мы уже говорили о преимуществах двоичной системы счисления с технической точки зрения организации работы компьютера. Зачем нужны другие системы счисления, кроме, естественно, еще и десятичной, в которой человек привык работать? Чтобы ответить на него, возьмем любое число в десятичной системе счисления, например 255, и переведем его в другие системы счисления с основаниями, кратными двойке:
Чем меньше основание системы счисления, тем больше разрядов требуется для его записи то есть, тем самым мы проигрываем в компактности записи чисел и их наглядности. Поэтому, наряду с двоичной и десятичной системами счисления, в вычислительной технике применяют так же запись чисел в 8-и 16-ричных системах счисления. Поскольку их основания кратны двойке, они органично связаны с двоичной системой счисления и преобразуются в эту систему наиболее быстро и просто (по сути они являются компактными видами записи двоичных чисел). Все другие системы счисления представляют для вычислительной техники чисто теоретический интерес.
Решение задач
1. Какое число записано с помощью римских цифр: CLVI
Решение: Зная обозначения, запишем: С – 100; L – 50; V – 5; I – 1
Решение: Пользуемся формулой:
a1 = 3; a2 = B; a3 = F; a4 = A
Следовательно: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*16 0
Ответ: 3ВFA16 = 3*16 3 + B*16 2 + F*16 1 + A*160
3. Запишите в свёрнутой форме число 1*8 2 + 4*8 1 + 7*8 0
Решение: Пользуемся формулой:
Следовательно: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Ответ: 1*8 2 + 4*8 1 + 7*8 0 = 1478
Алгоритмы перевода в системы счисления по разным основаниям
Алгоритм перевода чисел из любой системы счисления в десятичную
Алгоритм перевода целых чисел из десятичной системы счисления в любую другую
Алгоритм перевода правильных дробей из десятичной системы счисления в любую другую
Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую
Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2 n
Решение задач
1. Переведём в 10-ую с.с. число: 0,1235
Решение: Действуем строго по алгоритму перевода чисел из любой системы счисления в десятичную:
Найдём сумму ряда: 0,2 + 0,08 + 0,024 = 0,30410
Ответ: 0,1235 = 0,30410
2. Переведём число 12610 в 8-ую с.с. и число 18010 в 16-ую с.с.
Решение: Действуем строго по алгоритму перевода целых чисел из 10-ой с.с. в любую другую:
Во втором примере процесс можно продолжать бесконечно. В этом случае деление продолжаем до тех пор, пока не получим нужную точность представления. Записываем числа сверху вниз.
Ответ: 0,6562510 = 0,А816; 0,910 = 1,1110012 с точностью до семи значащих цифр после запятой.
4. Переведём число 124,2610 в шестнадцатеричную с.с.
Решение: Действуем строго по алгоритму перевода произвольных чисел:
Переводим целую и дробную часть:
Записываем полученные числа справа налево (в целой части) и сверху вниз (в дробной части).
Ответ: 124,2610 = 7С,428А16
5. Переведём число: 11001010011010101112 в шестнадцатеричную систему счисления
Решение: Действуем строго по алгоритму перевода чисел из 2-ой с.с в с.с. с основанием 2 n :