как быстро посчитать процент в уме
Как быстро и просто считать проценты в уме
В Интернете за каждой социальной сетью закрепилась определённая репутация, и так за Twitter — забавные истории и неожиданный лайфхаки. Уже никто не вспомнит, кто первым заговорил о том, как научиться считать проценты от числа и от суммы в уме, но способ оказался действительно простым и, что важнее, полезным для любого человека.
Британский копирайтер Бен Стивенс (Ben Stephens) назвал эту хитрость «маленьким лайфхаком». Суть его заключается в простой перестановке чисел, которая и помогает добиться искомого результата. Сама по себе методика не нова, однако колоссальная ответная реакция со стороны пользователей Сети доказывает, что многим она была незнакома.
Так как же научиться быстро считать проценты в уме:
Первое, что нужно сделать – перевернуть цифры.
«Допустим, вам надо извлечь 4% от 75 в голове, причем быстро. Как это сделать? Просто найдите 75% от 4, это намного проще». И в самом деле, 75% (то есть три четверти) от числа 4 равняются 3! Переворачиваем цифры обратно, проверяем. Снова 3! Работает!
Другой пример: найти 18% от 50. Звучит довольно сложно, но. Снова меняем цифры местами – и теперь нам надо найти 50% (т.е. половину) от числа 18. С этой задачей справится и ребенок.
Общую формулу Стивенс записывает так:
Буквально за несколько дней математический твит собрал свыше 5 тысяч репостов и 14 тысяч лайков. Оказалось, многие школьные преподаватели не рассказывали ученикам о таком фокусе. Даже сложно представить, как бы упростилась жизнь школьников и студентов, если бы они знали об этой формуле раньше. Но благо, этот способ, как быстро посчитать проценты, хранится в открытом доступе, а потому облегчит жизнь очень многим.
Сатурния
Сайт литературного объединения «Сатурния»
Как научится считать проценты в уме?
Филологам тоже нужно уметь считать, не так ли? Ведь мы имеем дело с числами каждый день — и в магазине, и по дороге, и в сочинительстве. Еще А.С. Пушкин говорил устами Моцарта: «Поверяйте алгеброй гармонию!».
А когда мы видим в магазине скидку на товар 30 %, то сразу начинаем вспоминать школьную программу: представляем составление пропорций или же бросаемся за помощью к калькулятору. Почему-то часто возникает стереотипное мнение, что считать проценты в уме сложно. На самом деле это не так. Зная несколько несложных правил, можно легко и быстро проводить подсчеты без помощи карандаша и листа бумаги или калькулятора.
Все хорошо помнят, как найти 50 % или 10 %. 50 % – это половина, и, чтобы посчитать ее значение, достаточно разделить число на 2. 10 % – это десятая часть, ее находят при разделении числа на 10. Отталкиваясь от этих умений, можно просто справляться с менее «удобными» для вычисления процентами. Логика расчета проста: нужно найти 50 или 10 % от числа, а дальше выяснить, как соотносится процент, который необходимо найти, с уже найденным.
Вот некоторые алгоритмы, которые могут пригодиться для быстрых операций:
По сути, такой способ – школьная пропорция, просто переведенная сразу в алгоритм, и в ней опущены нули, чтобы не запутаться. Этому методу легко научит хороший репетитор по математике на индивидуальных занятиях.
Но в этом случае есть один нюанс: если надо посчитать срочно и процент – не круглое число, тогда результат выйдет приблизительный, поскольку для удобства число придется округлить. Например, 68 к 70 или 23 к 20 или 25.
Как быстро считать проценты в уме: математическая хитрость.
Британский копирайтер Бен Стивенс (Ben Stephens) назвал эту хитрость «маленьким лайфхаком». Суть его заключается в простой перестановке чисел, которая и помогает добиться искомого результата. Сама по себе методика не нова, однако колоссальная ответная реакция со стороны пользователей Сети доказывает, что многим она была незнакома. Итак, первое, что нужно сделать — перевернуть цифры:
«Допустим, вам надо извлечь 4% от 75 в голове, причем быстро. Как это сделать? Просто найдите 75% от 4, это намного проще». И в самом деле, 75% (то есть три четверти) от числа 4 равняются 3! Переворачиваем цифры обратно, проверяем… Снова 3! Работает!
Другой пример: найти 18% от 50. Звучит довольно сложно, но… Снова меняем цифры местами — и теперь нам надо найти 50% (т.е. половину) от числа 18. С этой задачей справится и ребенок.
Общую формулу Стивенс записывает так:
Баяны
180K постов 12K подписчиков
Правила сообщества
Сообщество для постов, которые ранее были на Пикабу.
Автор, найди ка в своем умишке 21% от 179.
Вчера же уже повозили мордой по говну этого Бена.
Математик решил загадку числа 42
В течение 65 лет математики по всему миру пытались решить своеобразную головоломку и найти три числа, сумма кубов которых составила бы 42. И, кажется, им наконец удалось.
Задача звучит следующим образом: может ли любое число от 1 до 100 быть выражено как сумма трех кубов?
Если записать формулу 1954 года, то получится следующее: х^3 + y^3 + z^3 = K.
K в данном случае — любое число от 1 до 100. Соответственно, нужно было определить все три неизвестные переменные для каждого числа K в этом промежутке.
В последующие десятилетия были найдены решения для простых чисел. В 2000 году математик Ноам Элкис из Гарвардского университета опубликовал алгоритм, который помог найти более сложные. К 2019 году нерешенными остались только два самых сложных числа: 33 и 42.
Как и многие современные открытия, разгадке поспособствовал Youtube. Математик Эндрю Букер с канала Numberphile опубликовал решение задачи для числа 33, написав собственный алгоритм. Для этого ему понадобился мощный суперкомпьютер в Университете Advanced Computing Research Center, а решение удалось получить всего за три недели.
Итак, у нас осталось самое сложное число: 42. Для его решения Букер заручился поддержкой математика MIT Эндрю Сазерленда, эксперта в области массовых параллельных вычислений. В свою очередь, они прибегли к помощи Charity Engine — инициативы, которая охватывает весь земной шар, используя остаточную вычислительную мощность более 500 000 домашних ПК, в результате получая своего рода «планетарный суперкомпьютер».
Как быстро посчитать процент от числа
Умение мгновенно высчитывать проценты в уме пригодится в любой ситуации, например, чтобы быстро посчитать сумму скидки в магазине или банковский процент на кредит или вклад.
Есть множество способов высчитывать проценты. Самый простой – воспользоваться калькулятором процентов на телефоне, но не все калькуляторы снабжены подобной функцией или телефона нет под рукой.
Можно зайти в Интернет, и посчитать проценты онлайн. Но что делать, если нет Сети?
Вычисляем 10% от числа
Проще простого считать проценты-десятки от круглого числа. Все мы легко вычисляем 10% от 100 или 200, даже от 5000 каждый легко и просто вычислит 10 %.
Если перед нами 5500, то уже сложнее. Но здесь есть хитрость. Вычисляя 10 % от числа нужно смотреть на первые цифры, отделяя один последний знак запятой.
Например, 10% от 5500 = 550. здесь мы просто отделили последний 0.
10% от 550 будет 55, а 10% от 55 будет 5,5. 10% от 5,5 будет 0,55 и так далее.
Вычисляем 20% от числа
Посчитать 20% сложнее, но в случае с круглыми числами это проще. Нужно поделить число на 5.
Например: 100:5=20; 20% от 100=20.
4000:5=900; 20% от 4000=900.
Вычисляем 50% от числа
Легко вычислить 50% от числа – нужно просто поделить это число на 2.
Например: 50% от 11=11:2=5,5; 50% от 11=5,5.
Числа, которые не являются целыми, делите на калькуляторе, чтобы узнать точные 50%. Например, те же 5,5:2=2,75; 50% от 5,5=2,75.
Вычисляем любой процент от числа
Не все проценты высчитываются так легко. Но есть способ, с помощью которого можно посчитать целые проценты от целых чисел относительно быстро и просто.
Для этого нужно вспомнить простую школьную пропорцию:
Например, нам нужно найти 6% от 1850
Производим вычисления, где нам нужно 1850 поделить на 100 и умножить на 6.
Еще один способ заключается в том, чтобы сразу множить число на сотую часть необходимого процента.
Конечно, без калькулятора не обойтись, если нужно вычислить любой процент от сложного числа, но теперь вы знаете формулу, как легко можно посчитать проценты:
Делим число процентов на сто и умножаем на число, из которого этот процент вычисляем.
Вот так просто высчитывать сложные проценты из любых чисел. Круглые небольшие числа в таком случае можно вообще множить и делить в уме, так что вам не нужно больше долго раздумывать над тем, какой величины скидку вы получите в магазине.
Как посчитать проценты: от числа, от суммы чисел и др. [в уме, на калькуляторе и с помощью Excel]
Доброго времени суток!
Проценты, скажу я вам, это не только что-то «скучное» на уроках математики в школе, но еще и архи-нужная и прикладная вещь в жизни 👌 (встречаемая повсюду: когда берете кредит, оцениваете скидку, считаете прибыль и т.д.).
И на мой взгляд, при изучении темы «процентов» в той же школе — этому уделяется чрезвычайно мало времени. Возможно, из-за этого, некоторые люди попадают в не очень приятные ситуации (многие из которых можно было бы избежать, если бы вовремя прикинуть что там и как. ).
Собственно, в этой статье хочу разобрать наиболее популярные задачи с процентами, которые как раз встречаются в жизни (разумеется, рассмотрю это как можно на более простом языке с примерами). Ну а предупрежден — значит вооружен 😉 (думаю, что знание этой темы позволит многим сэкономить и время, и деньги).
И так, ближе к теме.
Как посчитать проценты: примеры
Вариант 1: расчет простых чисел в уме за 2-3 сек.
В подавляющем большинстве случаев в жизни требуется быстро прикинуть в уме, сколько там это будет скидка в 10% от какого-то числа (например). Согласитесь, чтобы принять решение о покупке, вам ненужно высчитывать все вплоть до копейки (важно прикинуть порядок).
Наиболее распространенные варианты чисел с процентами привел в списке ниже, а также, на что нужно разделить число, чтобы узнать искомую величину.
Задачка! Например, вы хотите купить технику за 197 тыс. руб. Магазин делает скидку в 10,99%, если вы выполняете какие-нибудь условия. Как это быстро прикинуть, стоит ли оно того?
Точный расчет : 197*10,99/100 = 21,65 тыс. руб.
Диаграмма с процентами / в качестве примера
Вариант 2: используем калькулятор телефона на Андроид
Когда результат нужен более точный, можно воспользоваться калькулятором на телефоне (в статье ниже приведу скрины с Андроида). Пользоваться им достаточно просто.
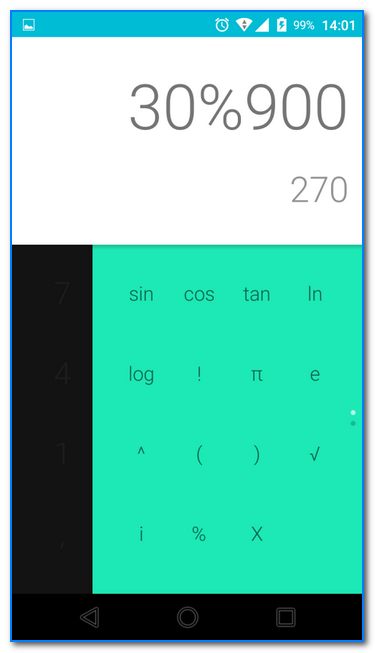
Например, вам нужно найти 30% от числа 900. Как это сделать?
Да достаточно легко:
30% от числа 900 (калькулятор Андроид)
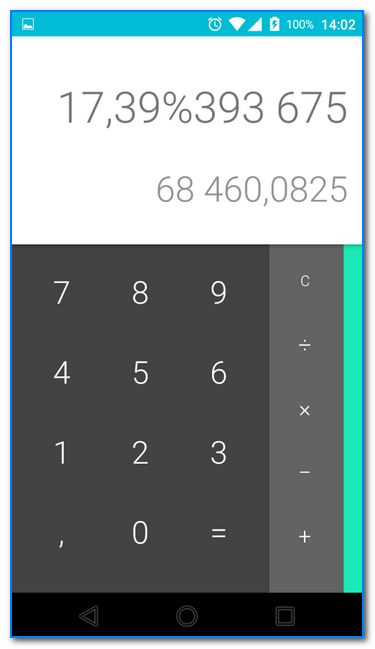
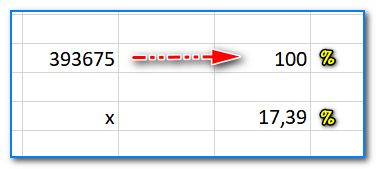
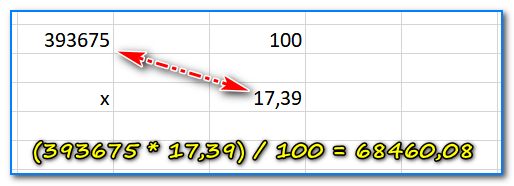
Ниже представлен более сложный пример. Нашли 17,39% от числа 393 675 (результат 68460,08).
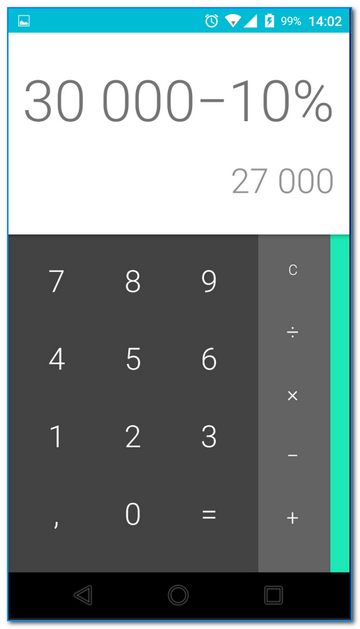
Если вам нужно, например, от 30 000 отнять 10% и узнать сколько это будет, то вы можете так это и написать (кстати, 10% от 30 000 — это 3000).
От числа отнимаем 10% (еще один пример)
В общем-то, весьма удобный инструмент, когда нужно просчитать 2-3 числа и получить точные результаты, вплоть до десятых/сотых.
Вариант 3: считаем процент от числа (суть расчета + золотое правило)
Не всегда и не везде можно округлять числа и высчитывать проценты в уме. Причем, иногда требуется не только получить какой-то точный результат, но и понять саму «суть расчета» (например, чтобы просчитать сотню/тысячу различных задачек в Excel).
В этих случаях рекомендую запомнить одно «золотое» правило столбика. Если вы поймете его — то без проблем сможете всегда решать задачки с процентами.
Допустим нам необходимо найти 17,39% от числа 393 675. Решим эту простую задачку.
Записываем числа для расчета процентов
Крест на крест (считаем проценты)
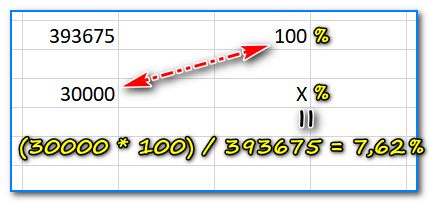
Чтобы снять все точки на «Й», рассмотрю обратную задачу. Например, сколько процентов составляет число 30 000 от числа 393 675.
Обратная задачка с процентами
Вариант 4: считаем проценты в Excel
Excel хорош тем, что позволяет производить достаточно объемные расчеты: можно одновременно просчитывать десятки самых различных таблиц, связав их между собой. Да и вообще, разве вручную просчитаешь проценты для десятков наименований товаров, например.
Ниже покажу парочку примеров, с которыми наиболее часто приходится сталкиваться.
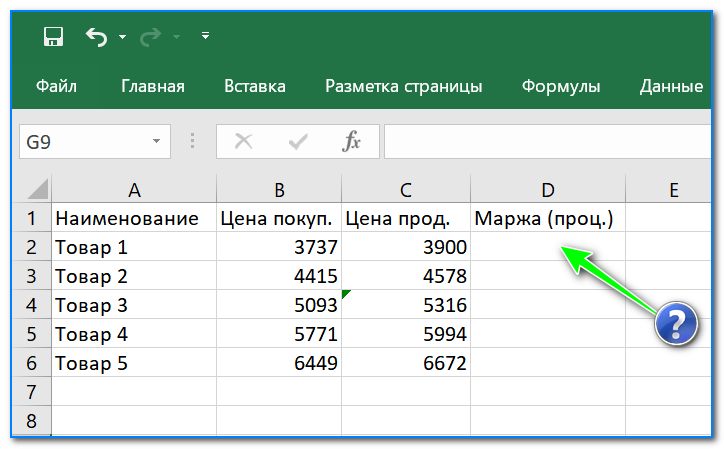
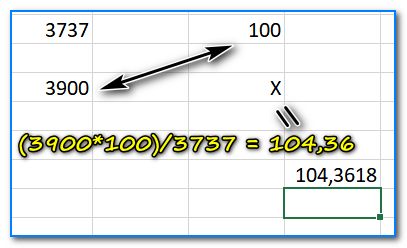
Задачка первая. Есть два числа, например, цена покупки и продажи. Надо узнать разницу между этими двумя числами в процентах (насколько одно больше/меньше другого).
Как определить, насколько одно число больше другого в процентах
Второе число составляет 104% от первого
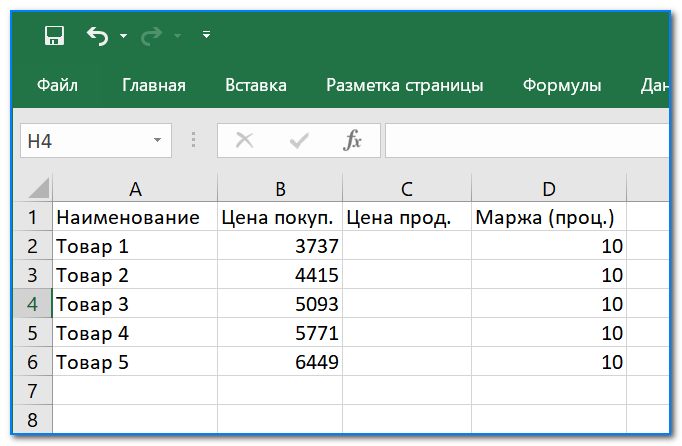
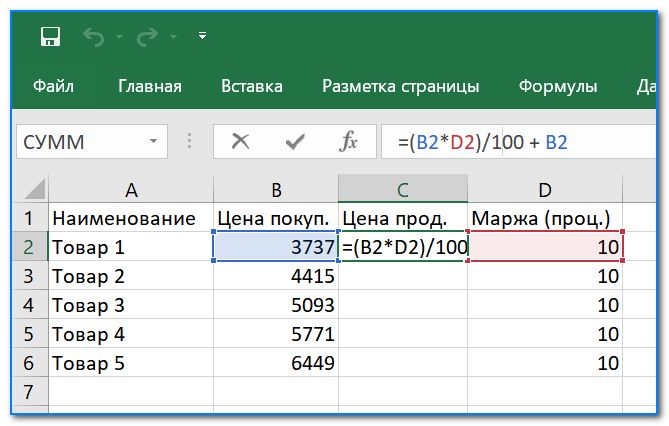
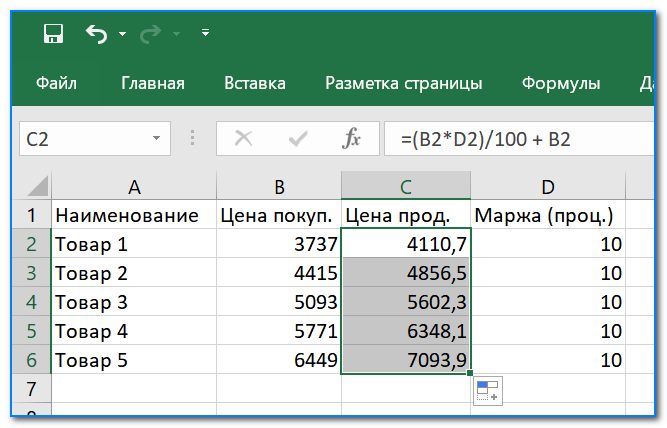
Для более точного понимания, приведу еще один пример. Другая задачка: есть цена покупки и желаемый процент прибыли (допустим 10%). Как узнать цену продажи. Вроде бы все просто, но многие «спотыкаются».
За какую цену продавать, если нужна маржа в 10%
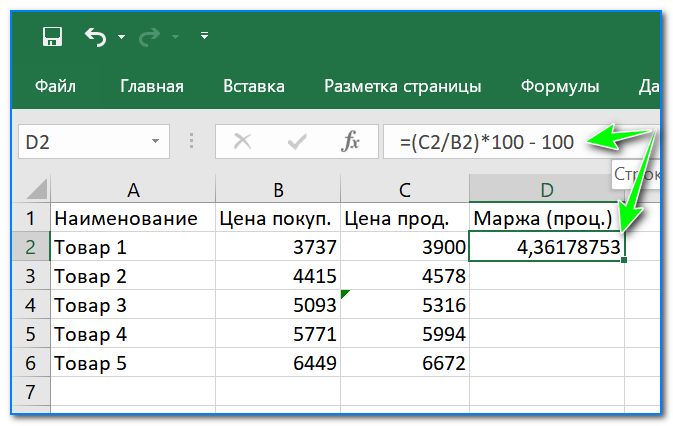
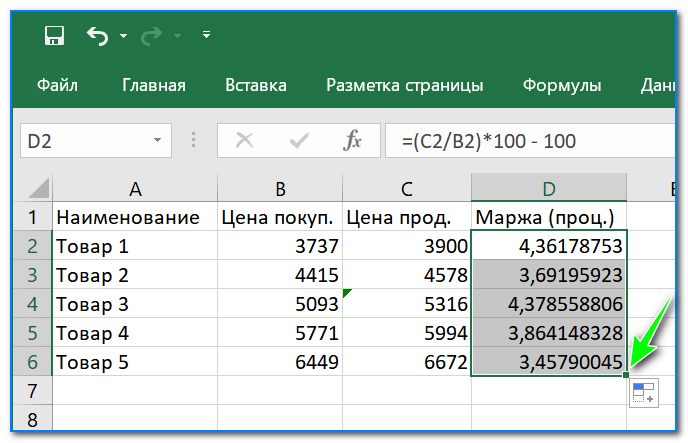
Считаем, насколько одно число больше другого в процентах
Пишем формулу для нашей задачи