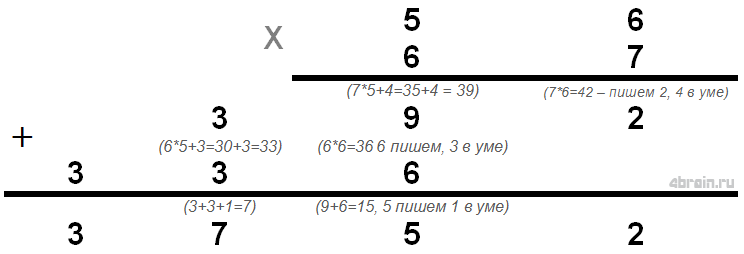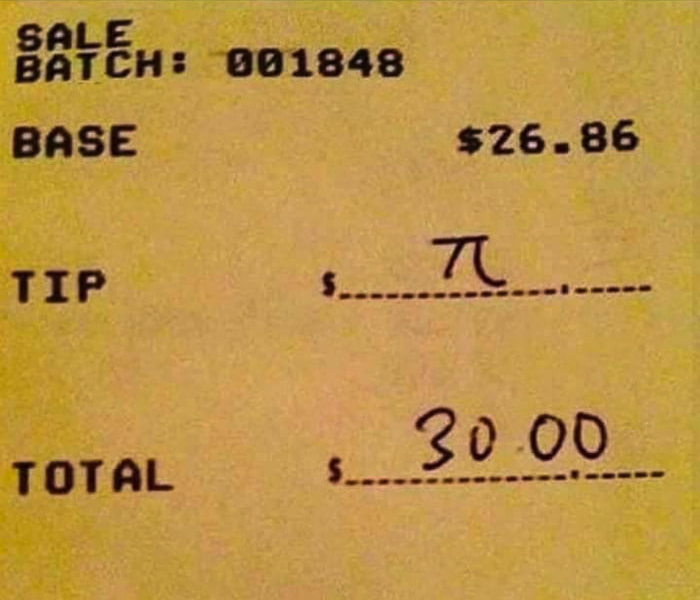как быстро умножить двузначное число на двузначное в уме
Урок 3. Традиционное умножение в уме

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Эффективный счёт в уме или разминка для мозга
Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:
Используем круглые числа
Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:
Т.к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.
Еще пример:
Упростим умножение делением
При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):
Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,
Теперь не кажется невозможным умножить в уме 625 на 53:
Возведение в квадрат двузначного числа
Оказывается, чтобы просто возвести любое двузначное число в квадрат, достаточно запомнить квадраты всех чисел от 1 до 25. Благо, квадраты до 10 мы уже знаем из таблицы умножения. Остальные квадраты можно посмотреть в нижеприведённой таблице:
Приём Рачинского заключается в следующем. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю. Например,
В общем случае (M — двузначное число):
Попробуем применить данный трюк при возведении в квадрат трёхзначного числа, разбив его предварительно на более мелкие слагаемые:
Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.
Умножение двузначных чисел
Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:
Составив их произведение, получим:
Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.
Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:
У этого приёма есть частный случай: всё значительно упрощается, когда у двух сомножителей одинаковое число десятков. В этом случае число десятков умножается на следующее за ним число и к полученному результату приписывается произведение единиц этих чисел. Посмотрим, как элегантен этот приём на примере.
48 x 42. Число десятков 4, последующее число: 5; 4 x 5 = 20. Произведение единиц: 8 x 2 = 16. Значит,
99 x 91. Число десятков: 9, последующее число: 10; 9 x 10 = 90. Произведение единиц: 9 x 1 = 09. Значит,
Ага, то есть, чтобы перемножить 95 x 95, достаточно посчитать 9 x 10 = 90 и 5 x 5 = 25 и ответ готов:
Тогда предыдущий пример можно вычислить немного проще:
Вместо заключения
Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.
Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».
Быстрый способ умножения двузначных чисел
Ну а ничего, что такой способ годится только для вариантов, когда одно из чисел от 90 до 99. Иначе :
Запоминать способ для вариантов, где один из множителей в диапазоне 10 чисел.. ну несерьезно, передай Кондрашеву А.А.
А я лет с 11-13 научилась умножать в уме числа 3х, 4х значные, 5тизначные на 2хзначные, например. Я просто в уме вижу перед собой листок и решаю на нем пример, элементарное умножение в столбик.
Конечно, эту процедуру можно и на листочке производить, но листочек память не тренирует)))
А двухзначные раскладываю на близкие круглые числа, потом прибавляю или отнимаю недостающие единицы
Нечётные чуть длиннее, например 79*95
5*9=45
5*70=350
+45=395
90*9=810
90*70=6300
+810=7110
+395=7505
Способ универсальный, от простого к сложному, подходит и для многозначных в любых комбинациях, ограничение только по количеству цифр, которое может запомнить мозг.
Была статья на хабре)
Там гораздо круче, несколько способов.
И этот, в том числе, был
По мне так проще всего так:
95*88=
1. 95*8=720+40=760
2. 760*10=7600 (конечно только в случаях 88 99 33 66)
3. 7600+760=8360
Это шутка?
Почему ЭТО работает
Несколько лет назад по интернету гуляла интригующая картинка
Многие уже успели проверить это для разных пар чисел. Сегодня я хочу показать, почему это работает для любых чисел, близких к сотне. И, что самое забавное, не только для них.
Не будем забивать пост картинками и шутками, а сразу перейдем к делу.
Допустим, у нас есть два числа, которые мы хотим перемножить. Назовем их a и b. Тогда, по вышеуказанному способу нам нужно отнять эти числа от 100 (получим 100-а и 100-b), вычесть их сумму из 100 и умножить результат на 100, получив таким образом разряд сотен. Чтобы получить разряд единиц, числа 100-a и 100-b нужно перемножить. Сложив сотни и единицы, получим предполагаемый результат умножения. Запишем это формально:
Раскроем еще одни скобки:
В итоге, раскрывая до конца:
Получаем верное тождество, выполняющееся для любых чисел
Интересно, что при доказательстве не использовалось, что a и b должны быть меньше 100. Давайте перемножим этим способом, скажем, 456 и 789:
Умножим на 100, получим 114500. Это «как бы» разряд сотен, хотя тут есть уже и тысячи и десятки тысяч и т.д.
Сложим эти числа, получим
245284 + 114500 = 359784
Перемножив числа 456 и 789 на калькуляторе или в столбик, получим такой же результат.
Спасибо за внимание)
Четыре недели
Так вышло, что срочно понадобилось снять квартиру на месяц, сдавать никто не хотел на такой короткий срок и пришлось искать посуточную.
Диалог с одной владелицей квартиры:
— 1100, у Вас не выйдет 4 недели.
— Как не выйдет? 29 дней.
— Ну это же не четыре недели!
— В неделе сколько дней?
— Ой, знаете, сейчас у меня календаря рядом нет, смотреть Вам еще тут.
*перезванивает через полчаса*
— Знаете, я тут проверила, и правда если 29 дней, то 4 недели выходит. Давайте по 1000
Как крупье считают ставку
Один из важнейших навыков крупье это в считанные секунды посчитать сколько выиграл победный номер.
Опытный крупье считает эту ставку быстрее чем вы это сделаете на калькуляторе.
Каждый чипс дает определенные выигрыши, например если поставить на линию между 11 и 12, это означает что вы покрываете сразу два числа и если выпадет 11 или 12 то вам заплатят 17 к 1.
Чем больше чипс покрывает номеров, том меньше коэффициент.
1 номер называют Страйт ап = 35 к 1
2 номера сплит = 17
3 номера стрит = 11
4 номера корнер = 8
6 номеров сикс лайн = 5
И вот на картинке у нас: (11 номер выпал)
3 раза по 35
3 раза по 17
2 раза по 8
4 раза по 5
3 раза по 11
Такой вот пример, и считать такую ставку нужно очень быстро, секунд за 5-15
(На фото сделан сетофф в разные стороны просто что бы было видно)
Вот еще фото, посчитайте сами и пишите в комменты что получилось без помощи калькулятора)) если вы посчитали в уме хотя бы за 45 секунд то скорее всего вы либо крупье, либо математик)
Чаевые математика
Турция и математика.
У среднестатистического жителя Турции математика вызывает благоговейный страх. Обычно это самый сложный предмет в школе.
Маленькая история как я прослыла звездой математики среди подружек.
Минут 15 я потратила на то, чтобы объяснить «аудитории», что старый автобус может вообще сломаться на обочине, если ему приспичило, а скорость нового автобуса от этого никак не зависит. Чувствую, что до конца не убедила.
Быстрый устный счет
В общем, думаю любому может пригодиться пара секретиков быстрого счета. К сути.
Возвести в квадрат
Итак, нам дано число, например, 97. Требуется возвести его в квадрат.
Найдем ближайшее круглое число А = 100
Оно на 3 больше исходного, значит B будет на 3 меньше исходного. Остается перемножить A*B и прибавить 3^2, получив 100 * 94 + 3^2 = 9409.
Очевидно, это работает на любых числах: возведем в квадрат число 2018. Итак, думаю самый простой способ взять d=18, тогда получится (2018-18)(2018+18) + 18^2 = 2000 * 2036 + 18^2 = 4072000 + 18^2 = 4 072 324.
(хотя кто-то предпочтет знать отдельный метод для двузначных чисел, но я посчитал, что это частный случай, и пикабушникам это просто не нужно. Кстати, сколько будет 49.5^2?)
Перемножить два числа
Здесь довольно много способов.
3) Всегда остается старый, добрый способ посчитать поразрядно. То есть:
Целая часть корня числа
Итак, начинаем совсем грубо.
2) 100 ^ 2 = 10000 >> 2018.
3) Ок, пусть будет 50.
4) 50^2 = 2500 > 2018 (чегООО? Опять мимо?)
4) 1 500 000^2 = 1.5 ^ 2 * 1 000 000 ^ 2 = 2 250 000 000 000 F
6) 1 550 000^2 = 155^2 * 10^4^2 = (200 * 110 + 45^2) * 10^8 = (200 * 110 + 2025) * 10^8 = (22 000 + 2025) * 10^8 = 24 025 * 10^8 = 2 402 500 000 000 > F
Годный лайфхак:
Не дайте себя обмануть в магазине. Устный счёт для чайников и «гуманитариев».
Преподавая технические дисциплины, сталкиваюсь с тем, что у детей зачастую не возникает проблем при сложении чисел. А вот при вычитании долго думают и гораздо чаще ошибаются.
Думаю, такая же история знакома и взрослым.
Ну а раз уж складывать гораздо проще, чем вычитать, то обычно предлагаю детям и своим знакомым использовать такую фишку, как вычитать с помощью сложения.
Обычно дети схватывают моментально и начинают гораздо быстрее считать в уме и реже ошибаются.
если это 164-32, то обычно проблем не возникает, ведь у первого числа и число десятков и единиц больше, чем у второго и ответ дать просто.
Но как только появляется необходимость вычесть 126-78, то это часто приводит к ошибкам. А если это ещё и дробные числа, то совсем плохо.
Эта ситуация знакома и взрослым по необходимости быстро посчитать, сколько должен дать сдачи продавец.
Так в чем же фишка, и как использовать сложение при необходимости вычитания?
Между вычитаемыми числами нужно найти какое-нибудь круглое число. И чем «круглее», тем будет проще.
Вернёмся к примеру, 126-78. Какое круглое число находится между этими числами? Правильно, 100.
А теперь считаем, сколько нужно прибавить к 100, чтобы получить первое число? 26. А сколько нужно прибавить ко второму числу, чтобы получить 100? 22. Значит, наш ответ 26+22=48.
И второй пример выше:
Сколько нужно прибавить к 200, чтоб получить 435.3? 235.3.
Сколько нужно прибавить к 178.7, чтобы получить 200? 21.3.
Все знакомые, которых научил такому способу, говорят, что теперь у них не возникает проблем в магазинах, когда считают сдачу.
Искусство умножения двузначных чисел в уме
Люди всегда стремились найти лучшие способы выполнения вычислений. Чем стремительнее развивается прогресс, тем более актуальными становятся высокие математические способности. Даже тот человек, карьера которого не предполагает работу с цифрами, ежедневно вынужден прибегать к счету в уме. Походы за покупками, оплата коммунальных счетов, планирование семейного бюджета – все это требует большого количество подсчетов. Конечно, можно полагаться на технику, ведь в каждом современном смартфоне присутствует калькулятор. Но все же стоит помнить, что умение быстро считать – это возможность существенно оптимизировать свои собственные ресурсы, поэтому развивать такие навыки важно.
Умножение в уме
В современном мире цифры окружают нас везде. Ежедневно мы не задумываясь выполняем десятки и даже сотни простых арифметических действий, но, стоит только столкнуться с более сложными числовыми операциями, и большинство людей машинально потянется к калькулятору. Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.
Складывать и вычитать устно – этому человек учится еще в школе. Со временем, удается научиться без труда производить вычисления даже с большими значениями. Конечно, это утверждение справедливо только для простых операций, таких как сложение и вычитание, а вот умножение освоить уже не так легко. В школе от детей требуется научиться умножать только на множитель от одного до десяти, а более сложные подсчеты допустимо производить на бумаге. Таким образом, ученикам не прививается умение выполнять умножение больших чисел в уме, этим навыкам можно обучиться только дополнительно.
Умение быстро считать очень полезно, так как оно используется ежедневно. Поэтому сегодня придумано множество подходов к счету. Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.
Популярные методы устного умножения
Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:
Вариант 1. Умножение в столбик
Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.
Сначала необходимо умножить 34 на единицы второго числа: 34*3=102. Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142
Вариант 2. Умножение с разложением на десятки и единицы
Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.
Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.
Вариант 3. Умножение с большими числами
Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.
Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.
Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.
Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.
Быстрое умножение в уме больших чисел
Математики всех времен искали простые методы быстрого устного счета. Умножение и деление, в отличие от сложения и вычитания, являются более сложными операциями. Поэтому производить такие подсчеты в уме без должной подготовки сложно, тем более когда речь идет о многозначных числах. Проблема устного умножения в том, что не существует какого-либо универсального способа, который бы подходил вне зависимости от ситуации.
Мозг обычного человека не способен работать также быстро, как калькулятор. Мы склонны терять концентрацию, сбиваться, забывать результаты промежуточных операций. Поэтому стандартные способы устного умножения мало пригодны для повседневных задач. Они скорее являются хорошей разминкой для мозга, чем удобным инструментом. Но что делать, если быстро считать без подручных средств все же хочется?
Благодаря интернету можно найти немало информации по этому вопросу. Сегодня существует множество методик, позволяющих научиться складывать, вычитать, умножать и даже делить с моментальной скоростью. Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.
Лучший способ научиться устному счету
Ментальная арифметика – это не только уникальный способ счета без подручных средств. В основе этой методики лежит равнозначное развитие как левого полушария мозга, отвечающего за логику и анализ, так и правого, которое контролирует работу воображения и фантазии. Несмотря на то, что освоить ментальную арифметику может любой желающий, она все же больше подходит для изучения в раннем возрасте. Именно в детстве можно приобрести навыки, которые не забудутся со временем и сохранятся на всю жизнь.
Обучение ментальной арифметике – длительный процесс, который требует усидчивости и нацеленности на результат. Пройдет немало времени, пока ребенок сможет полностью освоить программу и научиться не только складывать и вычитать, но и умножать и делить многозначные числа. Родителям не всегда удается контролировать периодичность занятий своего ребенка, а также следить за тем, чтобы он выполнял все необходимые упражнения. Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.
Ученики, обучающиеся по этому направлению, сначала осваивают вычисления на древних счетах – абакусе. Когда базовые навыки закрепятся, наступает время для перехода к следующему, более сложному этапу. Теперь ученик постепенно привыкает представлять абакус в своем воображении и производить подсчеты уже на нем. Именно так и удается развить навык быстрого счета.
Благодаря занятиям ментальной арифметикой ребенок повышает успеваемость в школе, ведь теперь ему доступны не только простые вычисления в уме, но и быстрое умножение и деление. Количество времени, которое он тратит на выполнение домашних заданий, также сокращается. Так удается добиться большей продуктивности образовательного процесса в школе и дома. Навыки, приобретенные благодаря ментальной арифметике, сохранятся навсегда, что очень пригодится во взрослой жизни.