как на практике осуществить адиабатический процесс с газом
Адиабатический процесс



Адиабатический процесс. Если сосуд с расширяющимся газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. Q = 0. Процесс, происходящий при соблюдении этого условия, называется адиабатическим.
Уравнение первого начала термодинамики при учете условия Q = 0 принимает вид
0 = ΔU + A или A = – ΔU. (109)
Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательна (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают.
Адиабатический процесс можно реализовать практически и при отсутствии хорошей теплоизоляции. Но тогда необходимо вести процесс столь быстро, чтобы за время его осуществления не произошел сколько-нибудь существенный теплообмен с внешней средой.
Теплоемкость при адиабатическом процессе
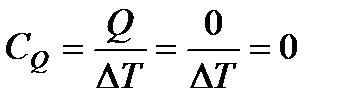
Выведем уравнение кривой, изображающей адиабатический процесс на рV-диаграмме. Уравнение состояния моля газа имеет вид:
При бесконечно малом изменении состояния совершаемая работа А = pdV, а изменение внутренней энергии, согласно (83), ΔU –> CVdT. Подставляя эти значения A и ΔU в уравнение первого начала термодинамики (109), получим:
Это есть уравнение адиабаты в дифференциальной форме. Поскольку оно содержит все три параметра — р, V и Т, — то для исключения одного из них воспользуемся уравнением состояния (111), предварительно продифференцировав его:
Умножая уравнение (112) на R, а (113) — на СV искладывая их, получим
Принимая во внимание, что для идеального газа CV + R = = Ср, разделим уравнение (114) на произведение CVpV и введем обозначение
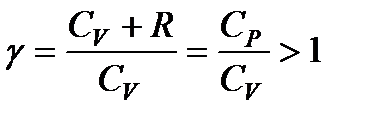
Тогда (114) примет вид
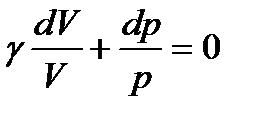
Учитывая, что постоянный множитель γ можно внести под знак дифференциала, преобразуем (116) к виду
Отсюда следует, что величина, стоящая в скобках, должна быть постоянной. Обозначим эту константу как ln(const). Тогда
γlnV + lnp = ln(const). (118)
Учитывая, что γlnV = lnV γ и потенцируя выражение (118), получим
Это и есть уравнение адиабаты. Его также называют уравнением Пуассона.
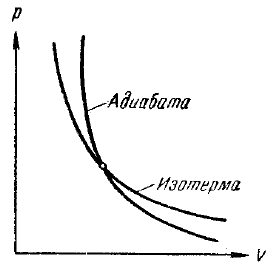
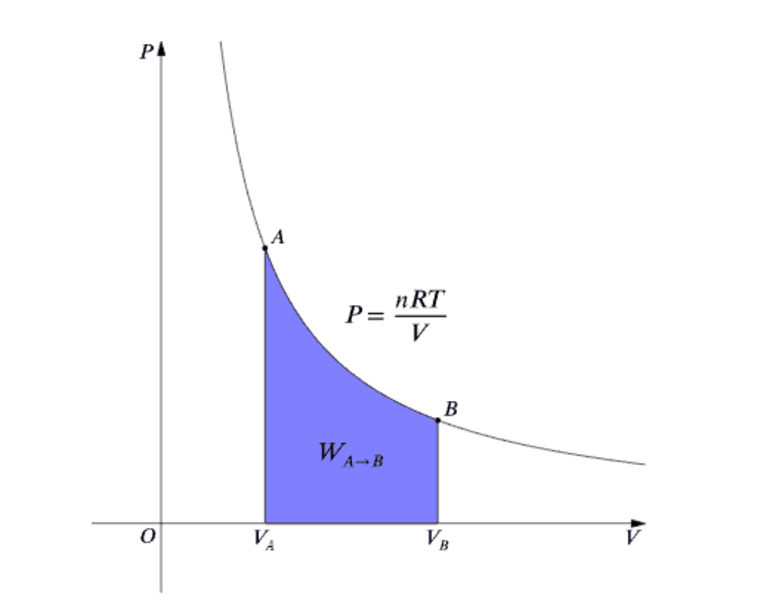
Поскольку γ > 1. то кривая, изображаемая этим уравнением (рис. 39), идет круче изотермы pV = const, которая для сравнения показана на том же чертеже штрих-пунктиром. Видно, что при адиабатическом расширении из точки I кривая (119) опускается ниже изотермы, т. е. газ охлаждается, а при адиабатическом сжатии кривая (119) поднимается выше изотермы, т. е. газ нагревается. Величина работы адиабатического процесса может быть особенно просто вычислена с помощью уравнения (109):
Используя формулу (115), выражение (120) можно преобразовать к виду:
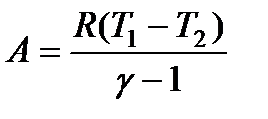
Для нахождения же конечной температуры T2 можно, комбинируя (111) и (119), получить соотношение
Для одноатомного газа Cv = 12,5 кДж/(кмоль*К), СP = Cv + R = 20,8 кДж/(кмоль*К), и показатель степени адиабаты равен примерно 1,67. Для двухатомных газов при обычных температурах 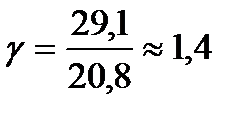
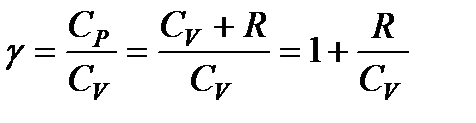
еще ближе к единице.
В быстроходных двигателях внутреннего сгорания и при истечении газов через сопла реактивных двигателей процесс расширения газа протекает настолько быстро, что его можно считать практически адиабатическим и рассчитывать по уравнению (119).
Рис. 39. Адиабата и изотерма
Так как у> 1, то из (122) следует, что при адиабатическом сжатии газ нагревается, а при адиабатическом расширении — охлаждается. Это явление находит применение в дизелях, где воспламенение горючей смеси осуществляется путем адиабатического сжатия. Нагревание газа при адиабатическом сжатии объясняется тем, что во время сжатия над газом производится работа, которая идет на увеличение его внутренней энергии. А так как внутренний энергия идеального газа зависит только от температуры, то это увеличение внутренней энергии проявляется в повышении его температуры. Аналогично объясняется и охлаждение газа при адиабатическом расширении. Охлаждение газа при адиабатическом расширении используется в холодильных машинах.
Физика. 10 класс
§ 14. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам изменения состояния идеального газа
В 9-м классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия?
Закон сохранения энергии. В середине XIX в. известный английский физик Дж. Джоуль (1818–1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814–1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX в. Г. Гельмгольца (1821–1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы.
Закон сохранения и превращения энергии: при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую.
Закон сохранения и превращения энергии является всеобщим законом природы и связывает воедино все физические явления. Этот закон выполняется абсолютно точно, на нём базируется всё современное естествознание.
Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1–2 °С. Что является причиной повышения температуры воды?
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи
Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.
Кратко об идеальном газе
Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.
Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:
Что это адиабатический процесс?
Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.
Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.
Уравнения Пуассона для адиабатического процесса
Первый закон термодинамики записывается в таком виде:
Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:
При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:
Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:
Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:
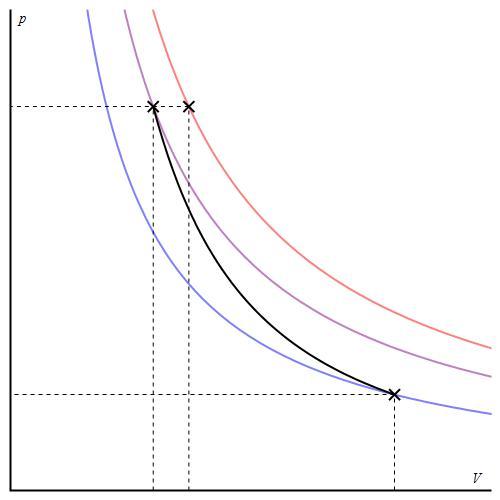
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.
Пример задачи
В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.
Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?
Для решения задачи следует использовать следующее уравнение адиабаты:
Его лучше записать в таком виде:
История открытия
Ряд экспериментов, проведенных в начале XIX столетия, доказали существование атмосферного давления. Так, немецкий инженер Герике сконструировал магдебургские полушария. Из сферы выкачивался воздух, после чего они с трудом разъединялись — воздух давил на них.
Пример еще одного исследования, целью какого является изучение такого явления — опыт Роберта Бойля. Физик доказал, что если трубка запаяна с короткого конца, а в длинный налита ртуть, последняя не поднимется до верха. Ведь воздушными потоками уравновешивается давящая сила.
Ламберт издал в 1779 году книгу «Пирометрия». В его труде описывается повышение и понижение температуры в приемнике воздушного насоса, когда движется поршень. Этот эффект подтвердили следующие ученые:
Дальтон опубликовал доклад, где называется особенность сгущения идеального газа. При нем выделяется тепло.
Обобщил накопившиеся знания Пуассон. По его мнению, температура при адиабатической реакции непостоянная, а, значит, закону Бойля — Мариотта необходима поправка — физик обозначил ее, как коэффициент k и выразил через соотношение теплоемкостей.
Важные нюансы
Термодинамический процесс в общем случае включает в себя теплообмен, работу, совершаемую системой и изменение внутренней энергии. Адиабатный по причине отсутствия обмена теплом сводится к последним двум.
Энтропия (S) не меняется в результате теплопередачи. Этот постулат описывается уравнением ΔS = ΔT=0. Здесь T — температура.
А также для расчетов используется такая величина, как адиабата идеального газа. Она обозначается буквой γ и вычисляется следующим образом: γ = C1/C2 (соотношение теплоемкостей).
Может подобный параметр выражаться и как количество степеней свободы. То есть γ = i + 2/ i.
Описание основных циклов
Физиками предлагается указанное определение процесса Карно: это идеальная цикличность, обеспечивающая работу тепловой машины с максимальным КПД. Наибольший и наименьший уровень разогрева совпадает с аналогичными показателями для рабочего устройства.
Среди условий для достижения нужного коэффициента полезного действия физики называют обратимость реакции, значит, следует исключить теплообмен между телами. Соответственно, преобразование тепла происходит лишь изотермически.
Обратный переход рабочего двигателя в исходную точку невозможен. Дело в том, что вся энергия затратится на восстановление изначального положения.
Работа четырехтактной двигательной системы осуществляется по схеме Отто, включающую в себя впуск, сжатие, рабочий вход и выпуск. Второй, третий и четвертый этапы считаются адиабатическими.
Прилагаемые в конце усилия равны разности мощности, с которой давят на газ и силы, затраченной на сжимание. Последнее повторяется до 7 раз (применяемая смесь зажигается принудительно).
Особенность адиабатической реакции заключается в невозможности теплообмена между окружающим пространством и объектом. С ее помощью можно объяснить, каким принципам подчиняется работа двигателя с четырьмя тактами и устройство с высокой отдачей.
Физика Б1.Б8.
Молекулярная физика и термодинамика
1. Введение
Основы молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана, Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика прочно утвердилась в науке. Непосредственным опытным подтверждением молекулярно-кинетической теории являются процесс диффузии, броуновского движения, распространения запаха и многие другие явления.
Движение каждой молекулы в веществе может быть описано законами классической механики. Однако число молекул в веществе чрезвычайно велико, направления и величины скоростей молекул совершенно случайны и непрерывно изменяются так, что становится невозможным охватить уравнениями движения всю совокупность молекул и сделать какие-либо выводы об их поведении.
Тем не менее, состояние вещества и его изменение определяется заданием небольшого числа определенных параметров, как температура, давление, объем, плотность и т.д., значения которых невозможно указать на основе решений уравнений классической механики. Дело в том, что свойства огромного числа молекул подчиняется особым, статистическим закономерностям. Статистическая физика изучает статистические закономерности, описывающие поведение большой совокупности объектов. Она основывается на теории вероятностей и позволяет вычислять средние значения величин, характеризующих движение всей совокупности молекул (средние скорости молекул, средние кинетические энергии, средние значения импульса и т. д.) и на этой основе истолковывает свойства вещества, непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом состоит суть молекулярно-кинетического изучения вещества.
Наряду со статистическим, существует термодинамический метод изучения вещества. В отличие от статистического метода термодинамический метод не интересуется строением вещества. Термодинамика изучают условия превращения энергии и характеризует их с количественной стороны.
В основе термодинамики лежит небольшое число закономерностей, установленных на основе большого числа опытных фактов и получивших название начала термодинамики.
У статистической физики и термодинамики общий предмет изучения – свойства вещества и происходящие в нем процессы. Подходя к изучению этих свойств с разных точек зрения, эти методы взаимно дополняют друг друга.
Совокупность тел, могущих обмениваться энергией между собой и с внешними телами, не входящими в эту систему, называется термодинамической системой. Одним из основных понятий термодинамики является понятие состояния системы. Состояние системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых термодинамическими параметрами (температура, давление плотность, теплоемкость, электропроводность и т. д.). Состояние системы называется стационарным, если значения всех термодинамических параметров не изменяются во времени. Стационарное состояние называется равновесным, если его неизменность не обусловлена протеканием каких-либо процессов во внешних по отношению к данной системе телах.
Исследования показывают, что параметры состояния тел взаимно связаны и могут быть выражены друг через друга. Поэтому термодинамическое состояние задается только ограниченным числом параметров состояния. Такие параметры называются основными параметрами состояния. Важнейшими параметрами состояния химически однородных систем являются плотность, объем, давление, температура. И между этими параметрами существует связь, выражаемая в виде математического уравнения