как называется математический склад ума
Что такое математический и гуманитарный склад ума
Типы мышления и склад человеческого ума
Из основ психологии известно, что за мыслительную функцию отвечают полушария мозга. Люди с доминирующим правым полушарием более эмоциональные, они отличаются образным, абстрактным мышлением. У таких личностей гуманитарный склад ума. Если же доминирует левое полушарие, человек является более практичным, обладает аналитическим мышлением и математическим складом ума.
Различают 5 основных категорий человеческого мышления:
— практический склад ума;
— художественно-образный;
— гуманитарный;
— математический (аналитический);
— универсальный склад ума (синтетический).
Каким типом мышления вы обладаете?
Для того чтобы понять свой тип мышления, в первую очередь вам необходимо ознакомится более подробнее с каждым из них.
Практический склад ума. Люди, которые им обладают, в повседневной жизни отдают предпочтение предметному мышлению. Они последовательны во всем и обладают неразрывной связью между предметом-пространством-временем. Человек с таким складом ума по своей сути реалист, не склонный фантазировать и мечтать.
Художественно-образный склад ума. При таком мышлении вся информация обрабатывается при помощи образов. Такие люди имеют развитое воображение и превосходный запас слов. Им проще рассказать, чем показать действием. Человека с художественно-образным складом ума очень легко распознать, так как он резко реагирует на критику и эмоционален практически во всех проявлениях. Аналитические способности у такой личности выражены значительно меньше.
Человеку, обладающему художественно-образным складом ума, прекрасно подойдут профессии психолога, социального работника, а также творческие профессии.
Гуманитарный склад ума, который можно охарактеризовать как знаковое мышление. Личность подобного склада обрабатывает информацию при помощи умозаключения. Такой человек не выстраивает логическую цепочку по «мелким деталям», а привязывает ее к конкретной воображаемой цели. В этом ему помогает развитая интуиция и творческое начало, которое основано на воображении и чувствах. Эмоциональный метод познания – это первое, на что опирается человек-гуманитарий.
Математическое (аналитическое) мышление имеет большое сходство с практическим складом ума.
Универсальное (синтетическое) мышление. Людей, обладающих таким складом ума, можно назвать счастливчиками, ведь они обладают всеми способностями. У них прекрасно развиты и левое, и правое полушарие. Они достаточно ясно представляют картину мира и хорошо разбираются в технических дисциплинах. Они эмоциональные реалисты. Однако эти способности разделены не поровну, а с некоторым перевесом. И чтобы выявить преобладающий тип мышления, необходимо пройти специальный психологический тест.
Исходя из вышесказанного, знания о типах мышления и складе ума имеют огромное влияние на ваше дальнейшее успешное будущее. Развивайтесь в правильном направлении! Успехов вам!
Что такое «математический склад ума» и почему наглядность в математике может быть вредной
Теории и практики
Математика — та область, в которой, пожалуй, наиболее ярко проявляется водораздел между «у меня нет способностей» и «меня неправильно учили». Хотя на самом деле все гораздо сложнее: важны не только «математический склад ума» и «наглядность преподавания», но и навыки коммуникации и даже язык, на котором ведется обучение. Все это изучает профессор Иллинойского университета Норма Пресмег, которая выступит на конференции «Психология и технологии в математическом образовании». По просьбе T&P директор по исследованиям «Яндекс.Учебник» Наталья Чеботарь поговорила с профессором Пресмег о пользе и опасностях математических визуализаций, правильном подходе к преподаванию и этноматематике.
— Давайте сразу внесем ясность: вы изучаете не математику, а тех, кто изучает математику…
— Есть большая разница между тем, чем занимаются математики, и тем, чем занимаются исследователи математического образования. Иногда математики думают, что они занимаются исследованиями, потому что они преподают математику, но часто они просто не знают о том, что математическое образование — это вот уже более 50 лет как совершенно отдельная область исследований. Всего 50 лет, хотя самой математике тысячи лет.
Большая часть моих работ основываются на работах советского психолога Крутецкого. Он проделал большую работу, которая, на мой взгляд, до сих пор не получила достаточного внимания. Сейчас я занимаюсь тем, чтобы показать, насколько его научные работы опередили свое время.
— Да, образование как область научных исследований часто упускают из виду.
— Вообще-то я сама считаю себя преподавателем математики, я 12 лет преподавала математику в старшей школе. И хотя у меня есть диплом математика, ученую степень я получала в Кембридже именно в области исследований математического образования. И исследование тех лет стало одной из самых потрясающих вещей, которые мне довелось сделать в жизни.
Это исследование началось прямо в классе: когда я преподавала математику в школе в ЮАР, я обратила внимание на нескольких учеников в моем классе. Они мечтали быть архитекторами, инженерами, для карьеры в этих областях им нужна была математика, но была одна проблема. Во время летних каникул они сдавали профориентационные тесты, и так получилось, что я была в комиссии проверяющих. И вот что я обнаружила: эти дети были невероятно одаренными в области пространственного мышления, всего 4% от всех сдававших экзамен могли показать такой уровень. Однако они полностью провалили математику, хотя многие разделы математики связаны с пространственным мышлением — и это не только геометрия, но и тригонометрия и даже алгебра (в работе с равенствами и формулами есть и визуальный компонент).
До этого я исследовала особенности креативного мышления Эйнштейна. Он любил думать картинками и вообще был отличным визуализатором. Я увидела связь: значит, все-таки возможно использовать визуальные образы для понимания математического материала. Но в ЮАР на тот момент не было никого, кто бы мог направить меня в моих исследованиях. Поэтому я отправилась в Кембридж, где нашла поддержку: коллеги считали, что вопрос, который меня беспокоил, нуждается в исследовании. Три года я пыталась понять, почему школьники, обладающие пространственным мышлением, не могут справиться с математикой.
— Удалось найти ответ?
— Да, и он был довольно неожиданным. Пришлось исследовать не только учеников, но и их учителей. На основе работ Крутецкого, который тоже изучал визуализацию как способ математического мышления у математически одаренных ребят, я разработала тесты — для учеников и учителей, и после того, как эти тесты были проверены на валидность, мы провели полевые исследования в выпускных классах школ. А затем я провела целый год, наблюдая за работой в классе, интервьюируя учителей и учеников.
Среди учащихся явно выделялись 54% «визуализаторов», тех кто предпочитает картинки, — но, выбирая стратегии для работы с классом, учителя редко ориентировались на них. Однако нашлось пять учителей, которые очень активно использовали визуализации в своей работе, — но корреляции между тем, насколько активно учитель использует визуальный материал в работе, и тем, какие результаты показывают его ученики-«визуализаторы», не обнаружилось.
Конечно, на уроках без визуализаций дети просто запоминают материал без глубокого понимания. Но и с визуальным подкреплением дела шли не лучше. Оказалось, что
дело не в визуализации, а в абстрактном мышлении, умении делать обобщения на основе этих визуализаций. Можно дать ученикам очень четкую картинку, прототип — и он просто не оставит места для анализа, додумывания.
— И как преподавать математику тем, кому она не дается?
— Среди всех участников исследования самым эффективным учителем оказался тот, кто использовал много визуализаций, но всегда вместе с заданиями на абстрактное обобщение этого визуального материала, додумывание. То есть — да, используйте цвет, линии и т. д., но если уж говорите о треугольнике, то задавайте вопросы и заставляйте думать. Важно не только представлять математику наглядно, но и иметь в виду трудности, которые сопровождают визуальное мышление.
Есть такое понятие — паттерны. Развивайте паттерное мышление. Скажем, если шахматиста-новичка попросить описать шахматную доску, он в деталях расскажет о шахматных фигурах. Опытные шахматисты видят вертикали, горизонтали, диагонали — паттерны, по которым перемещаются фигуры.
Именно паттерны, визуальные обобщения помогают в математике, в то время как конкретные изображения могут быть помехой на пути к пониманию математических понятий.
— И : существует такое явление, как талант к математике? Или математика подвластна всем?
— Вернусь к работам Крутецкого. Он работал в школах в конце 1930-х — тогда не было школьных тестов, не было данных. Если ученик не мог освоить математику, это однозначно была вина учителя. Так вот, Крутецкий и его коллега-исследователь Наталья Менчинская задались вопросом: как возможно, что дети одних родителей, которые учатся в одной школе у одного учителя, учатся по-разному? В своих исследованиях Крутецкий выдвинул гипотезу, что есть такая вещь, как математический склад ума. И если он присутствует, то он помогает ребенку видеть математику во всем. В те времена такая гипотеза — разделение детей на неспособных, способных и одаренных — не была популярной. Но результаты исследований показывали, что одни дети рассматривали каждую задачу как совершенно новую, а другие легко видели общее, находили параллели с тем, что они когда-то раньше решали, выделяли принципы решений.
Математический склад ума — это некоторый способ думать, который одним дается проще, а другим сложнее. Если ребенку сложно с математикой — возможно, стоит поискать другие области, где ему легче. Тем не менее внимательный учитель должен помочь каждому увидеть общее в разных задачах и научить не страдать над ними, а получать удовольствие от решения.
Математические культуры
— Вы ведь еще занимаетесь этноматематикой. Что это такое?
— Как я говорила, я работала в ЮАР. В Дурбанском университете около трети студентов были европейцами, треть — местное население, и треть — эмигранты из Индии. Это было еще в 1980-х, ситуация была напряженной, и было особенно важно учитывать разные культурологические нюансы. В университете я занималась обучением учителей и тогда поняла, насколько важно исследовать культуру, особенно в связи с обучением математике.
Многие считают математику предметом, независимым от культурных кодов, но это только так кажется.
Меня заинтересовали математические идеи, созданные в национальных культурах, и люди, которые этими идеями пользуются на практике.
Например, у австралийских аборигенов есть довольно сложная монархическая система. Она накладывает множество ограничений на браки с людьми за пределами сообщества, но также, естественно, и на браки с близкими родственниками. Чтобы определить, кому на ком можно жениться, у них придумана система, в которой участвуют диэдральные группы четвертого порядка — это довольно сложное математическое построение. Естественно, сами аборигены ничего такого не высчитывают, они просто проживают свою культуру. И вот именно такими вещами занимается этноматематика — cмотрит на культуры через математические очки. Даже здесь, в США, некоторые из моих студентов увлекаются шитьем традиционных пледов из лоскутов, а ведь узоры, которые передаются из поколения в поколение, — это тоже этноматематика.
— Изучает ли этноматематика влияние определенной культуры на математические способности?
— Я бы не сказала, что принадлежность к культуре дает детям определенные преимущества в математике. А вот что точно помогает, так это когда язык, на котором говорят с детьми дома, совпадает с тем, на котором говорят в классе. Когда эти языки различаются, дети действительно испытывают трудности в классе.
И, конечно, сам язык оказывает влияние.
Есть языки, которые вообще лучше приспособлены к математике
— например, японский, где «11» передается через слова «десять» и «один». В английском это будет отдельное слово «eleven» — что?! А во французском вообще считают двадцатками! Чтобы cказать «81», вам придется произнести «четырежды двадцать и один» — вы только представьте себе, как дети этому учатся.
— А насколько математические способности зависят от общего культурного уровня?
— Австралийский ученый Ллойд До исследовал влияние языковых барьеров на обучение: если ребенок мог преодолеть языковой барьер, он мог продвинуться в математике, но для тех, кто не смог овладеть языком свободно, сам язык оказывался препятствием. Была и гипотеза Сепира — Уорфа, которая говорила, что язык определяет способ мышления, но в дальнейшем многочисленные исследования опровергли некоторые ее утверждения.
Математика дается людям всех культур. Но есть разница между двумя типами «окультуривания» — культура, которую ты принимаешь от родителей, и культура, отличная от твоей родной, которую ты изучаешь. Если ребенок способен воспринимать новую для себя культуру, у него все получится.
Не можете решить задачу — поговорите об этом
— Вы выступаете на конференции, которая называется «Психология и технологии в математическом образовании». Несколько лет назад у многих было ощущение, что индивидуальные траектории в обучении — это вопрос нескольких лет, что совсем скоро современные онлайн-сервисы смогут научить, скажем, математике тех, кого не могли научить раньше. Кажется, эта задача намного сложнее, и сложности находятся скорее на стороне науки: мы до сих пор не очень хорошо понимаем, как разные люди учатся.
— Важно осознать, насколько важную роль в обучении играет хороший учитель. Я думаю, что хорошего учителя никакая машина никогда не заменит. Мои исследования ясно показывают: чтобы добиваться результата, преподаватели подстраиваются под разных учеников. И чаще всего это происходит на интуитивном уровне. Важнее всего понять, почему учащийся дает тот или иной ответ на задачу, — ответ может быть неправильным, но только преподаватель может определить причину неверного ответа. Есть трудноуловимые связи между людьми, вряд ли в ближайшие 20 лет компьютеры смогут их воспроизвести.
— Часто говорят, что учитель больше не источник знания, а человек, который создает образовательное пространство. Но из того, что вы говорите, следует, что роль учителя больше похожа на роль врача, который способен точно диагностировать причины ошибок, которые совершает ученик.
— Мне нравится ваша метафора. Учитель и диагностирует, и выдает лекарство. И неважно, насколько замысловатыми будут компьютерные решения, — компьютер никогда не сможет обеспечить такой уровень согласованности между людьми, не сможет точно диагностировать причину неудачи ученика в конкретном примере. Но это проблема, потому что одно дело — гипотетический учитель, который работает с учащимся один на один, и совсем другое — класс, в котором разные ученики думают и воспринимают информацию по-разному.
Мои исследования — тесты на предпочтительный вид мышления — показывают нормальное гауссовское распределение. Большая часть людей находится в центральной части «холма»: иногда им нужно больше визуального подкрепления, иногда оно не требуется. Это зависит от трех факторов — от самого задания, от инструкций к заданию, которые могут требовать выполнять задание только определенным образом, и от индивидуальных особенностей человека. Но вот по краям распределения как раз хорошо видны различия: с одной стороны находятся люди, которым всегда нужны картинки (они сами их нарисуют, если не получат от преподавателя), а с другой — те, кому картинки не нужны, они на них вообще внимания не обращают. Так вот представьте: у вас в классе такое вот распределение, а вы пытаетесь (вынуждены) всех учить одним способом.
Я верю, что помочь в этой ситуации могут несколько практик — обсуждения заданий в небольших группах и возможность ученика рассказать о своем решении всему классу, чтобы другие могли узнать о другом способе мышления. Важно оставлять в классе место для коммуникаций, развивать умение выражать словами математические идеи.
Математическое мышление
На сайте мы уже много раз говорили о самых разных видах мышления, но вот именно математическое мышление было незаслуженно обделено вниманием. Наконец-таки мы исправим это упущение. Однако у вас может возникнуть вопрос: «А зачем мне вообще это математическое мышление?». Поэтому сначала вкратце объясним, что это такое, и почему важно уметь думать, как математик.
Что такое математическое мышление и в чем его польза?
Определение математического мышления таково: математическое мышление – это абстрактное теоретическое мышление, объекты которого лишены вещественности, но при этом они могут быть интерпретированы любым произвольным образом с одним лишь условием – должны сохраняться заданные между объектами отношения.
Учитывая то, что математика – это наука не только об уравнениях и формулах, но и о структурах, порядке и отношениях, главное отличие математического мышления от обычного (повседневного) состоит в том, что оно прививает и развивает у человека навык критического восприятия окружающего мира, желание и умение «копнуть глубже» и найти истину, понять причины и суть самых разных понятий и явлений.
Если говорить о практической пользе математического мышления, то в первую очередь (ведь об этом говорит само его определение) на ум приходит, конечно, то, что оно помогает нам справляться с математическими задачами. Однако истинная его ценность намного больше.
Человек, у которого развито математическое мышление:
Если говорить конкретнее, то умение мыслить, как математик, способствует успехам в учебе, ведь человек привыкает разбивать сложные задачи на более мелкие, удерживать в голове большое количество информации и оперировать ей, справляться с трудностями, выявлять взаимосвязи. Причем все это может пригодиться как в математике, так и в любой другой науке.
Математически мыслящий человек обладает навыком критической оценки информации, ведь окружающая действительность воспринимается им с некоторой долей здорового скептицизма. Это помогает различать правду и вымысел, опираться на факты и доказательства, а не слепо верить тому, что говорят.
Кроме того, математическое мышление помогает в принятии жизненно важных решений. Любая проблема и трудность раскладывается на составляющие, во внимание берутся все вероятные исходы и последствия. А благодаря уверенности в решаемости любых проблем человек охотнее берет на себя ответственность, менее подвержен страхам и сомнениям, может в любой ситуации придумать план действий.
Еще один полезный аспект развитого математического мышления состоит в том, что оно помогает преодолеть злосчастную привычку откладывать дела на потом, нерешительность перед сложными задачами. А все это вместе взятое служит тем самым стержнем, на котором держатся все составляющие успешной, образованной, уверенной в себе и самостоятельной личности. И это самым прямым образом влияет на достигаемые человеком в жизни и работе результаты.
Посмотрите это видео, в котором математик Эдуардо Саенц де Кабезон на конференции TED в остроумной манере рассказывает о пользе математики в жизни.
Таким образом, математическое мышление является навыком, необходимым каждому, кто стремится к достижению высоких целей. Но перед тем как начинать развивать его, необходимо хотя бы в общих чертах понять его природу.
Особенности математического мышления
Ученые уже не один десяток лет пытаются понять, откуда вообще в человеке есть способность к проведению математических вычислений. Для объяснения этого феномена предложены две теории. Смысл первой сводится к тому, что склонность к математике – это побочный эффект появления речи и языка. А вторая говорит, что причиной всему возможность применения интуитивного понимания пространства и времени, причем корни этого понимания тянутся вглубь веков.
Пытаясь понять, какая же теория верна, психологи провели эксперимент, для которого взяли 15 обычных людей и 15 математиков с одним и тем же уровнем образования. Обеим группам предлагали несколько сложных математических и нематематических утверждений, и участники должны были оценить их истинность, ложность или бессмысленность. Во время эксперимента мозг каждого испытуемого сканировался томографом.
В результате выяснилось, что заявления, касавшиеся математических областей (геометрии, алгебры, топологии, анализа и т.д.), возбуждали участки префронтальной, нижневисочной и теменной коры головного мозга только у математиков, но не у второй группы испытуемых. И эти зоны отличались от тех, что активизировались у каждого испытуемого при обработке нематематических утверждений. Вышеназванные зоны «работали» у обычных людей только тогда, когда они решали простейшие арифметические задачи.
С научной точки зрения этот результат объясняется тем, что математическое мышление более высоких уровней задействует нейронную сеть, отвечающую за восприятие времени, пространства и чисел. И эта нейронная сеть отличается от той, что связана с языком. Это приводит нас к выводу, что на развитие математического мышления непосредственно влияет развитие пространственного мышления. Кстати, чтобы понять, как математика взаимодействует с психологией и другими науками, можете почитать книгу «Математическое мышление» выдающегося немецкого математика и физика-теоретика Германа Вейля.
Еще одна особенность математического мышления состоит в том, что в его структуре выделяются несколько пересекающихся подструктур, называемых типами математического мышления (эта идея была предложена кандидатом психологических наук Ильей Яковлевичем Каплуновичем). От того, какой из этих типов доминирует, зависит мыслительная деятельность человека в любой практической ситуации.
Типы математического мышления
Всего можно выделить пять типов математического мышления. Расскажем о них в тезисной форме:
Эти типы математического мышления развиты в каждом человеке в разных пропорциях. У большинства людей преобладает порядковое мышление, причиной чему служит, помимо прочего, стандартная система школьного образования, работающая именно по порядковой схеме.
Определить свой преобладающий тип математического мышления можно при помощи специализированных тестов, которые можно найти в Интернете. Но можно и просто понаблюдать за своими повседневными действиями. Попробуйте, например, описать свою комнату, перечислить все, что в ней есть, а затем оцените свой ответ:
И еще один интересный факт: люди, у которых преобладает один и тот же тип мышления, неосознанно тянутся друг к другу, т.к. им часто сложно понять систему мышления тех, кто от них отличается. Но давайте отойдем от типологии и теории, и уделим внимание основной теме нашей статьи и практической части.
Основываясь на результатах эксперимента, о котором мы рассказывали выше, можно сделать вывод о том, как развить математическое мышление: нужно развивать мышление пространственное. И сейчас мы расскажем о том, как это делается (а в конце статьи предложим несколько рекомендаций по развитию математического мышления вне зависимости от пространственного).
Пространственное мышление: определение и развитие
Пространственное мышление необходимо нам для решения множества задач, которые ставит жизнь. Речь здесь в первую очередь идет о пространственном воображении – способности детализировано представлять трехмерные объекты. С помощью нее мы можем манипулировать любой воображаемой или реальной пространственной структурой, оценивать ее пространственные отношения и свойства, видоизменять ее и создавать новые структуры.
Пространственное мышление является совершенно особым видом деятельности, имеющим огромное значение для решения задач, которые ставят нас перед необходимостью ориентироваться в теоретическом или практическом пространстве. В наиболее развитой форме пространственное мышление – это мышление при помощи образов, в которых фиксируются пространственные отношения и свойства.
Психология уже давно говорит о том, что зачатки пространственного мышления присутствуют с рождения у ничтожно малого количества людей, а потому оно нуждается в развитии. Заниматься этим полезно любому человеку и в любом возрасте. И важно это не только потому, что развивается математическое мышление, но и потому, что такая деятельность обеспечивает нормальное функционирование мозга, служит профилактикой множества заболеваний, вызываемых дефицитом работы нейронов.
Если затронуть конкретно развитие у детей, то пространственное мышление повышает успехи в освоении технических наук и даже изучении литературы, ведь оно позволяет создавать в сознании целые динамические картины, основанные на прочитанных текстах. Соответственно, ребенку становится легче анализировать художественные произведения; повышается интерес к чтению. Ну а о том, что пространственное мышление пригодится на любимых детьми уроках труда и рисования, пожалуй, и говорить не стоит.
Несмотря на то, что в той или иной степени пространственное мышление развивается в человеке с детских лет, уже к подростковому возрасту это развитие останавливается. Но при желании можно самостоятельно его развивать и совершенствовать. Для этого используются специальные упражнения (их можно применять для развития у детей и у взрослых).
Упражнение «Представление»
Задача – просто представлять какие-то объекты. Проще всего – линии и отрезки. Вот несколько примеров:
Упражнение «Угадывание на ощупь»
Возьмите помощника. Закройте глаза и попросите его дать вам в руки какой-нибудь предмет, к примеру, фрукт, ткань, детскую игрушку, пульт от телевизора и т.д. На изучение объекта дается от 15 до 90 секунд (в зависимости от возраста и степени развития пространственного мышления). Отдайте предмет напарнику и скажите, что было у вас в руках.
Упражнение «Копирование»
Задания в этом упражнении постепенно усложняются. Алгоритм такой:
Упражнение «Муха в клетке»
Для начала найдите себе двух помощников. Двое из вас будут выполнять задание, а третий будет следить за игрой и проверять результаты.
Суть упражнения: вместе со своим помощником представьте решетку 9х9 квадратов (у третьего участника должна быть ее графическая схема, но вам ей пользоваться нельзя). В ее правом верхнем углу сидит муха. Определите очередность ходов и по очереди перемещайте муху по квадратам. Обозначайте движения и число клеток.
Например, вы передвигаете муху на 4 клетки вниз. Наблюдающий обозначает ваш ход на своей схеме. Так же он действует с каждым другим ходом. В какой-то момент он говорит: «Стоп», а вы со своим напарником должны сказать, в каком конкретно квадрате находится муха.
Победителем будет тот, кто даст правильный ответ (его должен подтвердить наблюдающий). Кстати, если хотите усложнить игру, можете изменить количество клеток решетки (она не обязательно должна быть симметричной).
В дополнение к этим упражнениям можно использовать и другие методы.
Схемы и чертежи
Опираясь на какой-то наглядный материал (или без него), например, на предметы в своей комнате, составляйте их планы, схемы и чертежи. Если взять комнату, то в ее плане должны присутствовать все предметы и их схемы. С тем же успехом можно рисовать чертежи зданий, магазинов, автомобилей и т.д.
Оригами и 3D-паззлы
Поищите в Интернете самоучители по оригами и учитесь складывать из бумаги различные фигурки. Также для этого подходят 3D-паззлы, которые можно купить в любом книжном магазине.
В начале работы представляйте желаемые фигуры и старайтесь определять необходимый порядок действий. Задания лучше всего усложнять:
Графические тренажеры
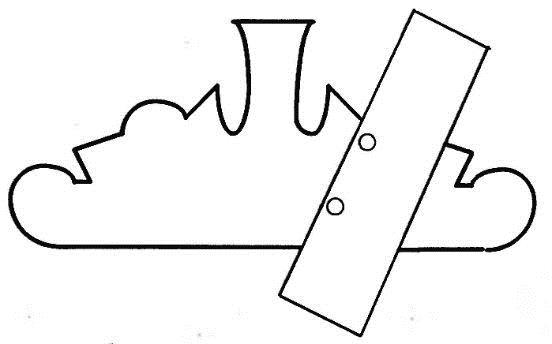
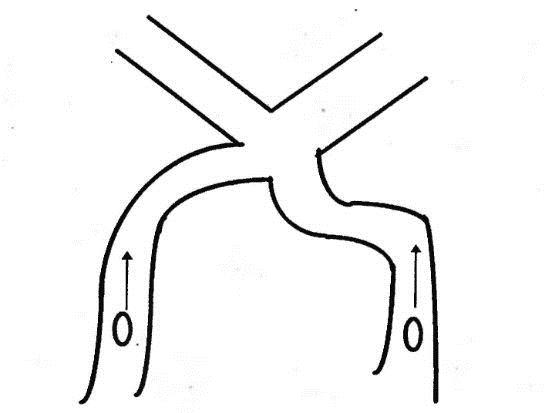
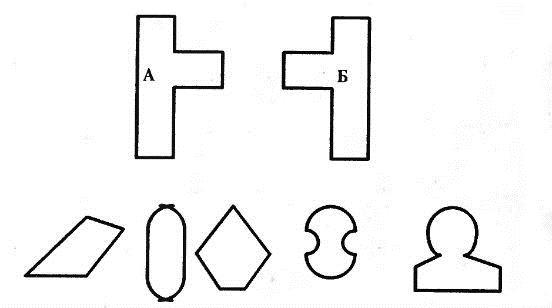
Сегодня есть множество графических тренажеров, созданных специально для развития пространственного мышления. В качестве примера мы взяли несколько изображений из книги известного детского педагога Израиля Зиновьевича Постоловского «Тренировка образного мышления».
Вот такими могут быть задания:
Это всего лишь несколько способов, как развить пространственное мышление, и при желании в Интернете можно найти немалое количество других упражнений и игр.
Теперь же давайте немного отстранимся от пространственного мышления и вернемся к математическому. Ниже мы приводим несколько рекомендаций по его развитию у детей и у взрослых.
Рекомендации по развитию математического мышления
Для развития математического мышления полезно заниматься развитием логики и как можно больше работать с цифрами. В первую очередь при необходимости любых вычислений в повседневной жизни старайтесь производить их в уме – без использования калькулятора.
Учитывая склонность мозга к тому, чтобы чаще не думать, чем думать, стремитесь активизировать активность интеллекта. Выполняйте специальные задачи и упражнения на логику, играйте в математические игры, решайте головоломки, ребусы и кроссворды, играйте в шахматы, пользуйтесь онлайн-тренажерами и тестами.
Обязательно правильно питайтесь, чтобы в ваш организм поступали все нужные ему витамины, минералы и микроэлементы. Чередуйте умственную деятельность с физическими нагрузками, т.к. физические упражнения позволяют мозгу отдохнуть, а также способствуют выработке организмом полезных гормонов.
А говоря о детском развитии, заметим, что развивать математический склад ума необходимо уже с малых лет. Оптимальным возрастом для начала занятий считается период от 1 до 3 лет, т.к. позже намного удобнее работать с уже частично сформированной у ребенка математической базой и развивать ее, нежели постигать азы.
Чтобы привить ребенку интерес к математике, нужно делать так, чтобы он воспринимал ее не как скучную прикладную науку, а как интересное занятие. Для этого полезно как можно чаще задавать разные задачки, использовать игрушки, считалки, активные игры на математическую тему, демонстрировать наглядные примеры простейших математических вычислений и их полезность. Правильное питание и физические нагрузки относятся и к детям тоже, причем даже больше, чем к взрослым.
Помимо прочего, предлагаем вам почитать наши статьи «Как объяснить ребенку математику?» и «Уроки математики для малышей», а также книгу «Как обучить вашего малыша математике» Гленна и Джанет Доман. А для вашей личной пользы советуем почитать книги «Математическое мышление» (Герман Вейль) и «Думай как математик» (Барбара Оакли) и посмотреть видео от российского математика и физика Алексея Семихатова о связи математики и интуиции.
Желаем вам удачи в обучении, и пусть математическое мышление помогает вам не только решать примеры, но и добиваться успехов в жизни!