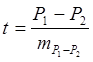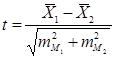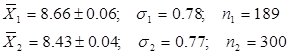какие параметрические критерии статистической достоверности используются в практике фкис

Практикум

М.В. Горшков
Экологический мониторинг
Учебное пособие. – Владивосток: Изд-во ТГЭУ, 2010. – 313 с.

Практикум

Тема 2. Статистическая обработка экологических результатов

2.2. Параметрические и непараметрические критерии

Статистические критерии, с помощью которых можно установить достоверность различия между параметрами (M, σ) вариационных рядов одноимённого признака в двух выборках (или в выборке и генеральной совокупности) называются параметрическими. Они используются при предположении, что распределения сравниваемых рядов близки к нормальному.

Критерий Стьюдента (t). Весьма известный критерий, предложенный У. Госсетом. Критерий Стьюдента для сравнения одноимённых параметров (P₁ и P₂) двух вариационных рядов имеет при n>20 в общей форме вид:

где в знаменателе стоит ошибка разности этих параметров, представляющая собою корень квадратный из суммы квадратов ошибок репрезентативности выборочных параметров:

.

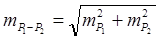
С учётом формул ошибок репрезентативности критерий t приобретает окончательный вид:

§ для сравнения средних арифметических:

§ для сравнения средних квадратических отклонений:

.

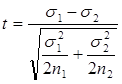
Оценка достоверности разницы производится с помощью сравнения полученного значения t со стандартным (t_st), взятым из соответствующей таблицы при выбранном уровне достоверности и числе степеней свободы.

Рассмотрим пример: Изучалось число лепестков венчика у Ficaria verna из двух популяций в окрестностях г. Пушкина Ленинградской области (1965 г.). Были получены следующие выборочные параметры:

Критерий t для определения достоверности разницы между средними:

.

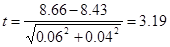
Критерий t для определения достоверности разницы между средними квадратичными отклонениями:

.

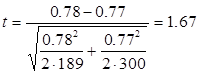
По таблице значений t_st при 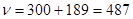(почти 500) t₀₁=2.59. Делаем вывод: две популяции Ficaria verna достоверно отличаясь по среднему признака совпадают по степени изменчивости числа лепестков.

Критерий Фишера (F) является более точным критерием сравнения средних квадратических отклонений. Он представляет собой отношение двух дисперсий:

,

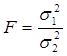
причём в числителе берут большую дисперсию их двух. Для вышерассмотренного примера имеем:

.

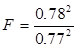
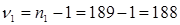
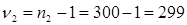
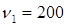
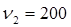
Из таблицы стандартных критериев Фишера находим, при и . Берём близкие значения по таблице: и . При 1%-ом уровне достоверности получаем F=1.39. Видим, что F 2 > χ 2 _st. То нулевая гипотеза об отсутствии различия между теоретическим и эмпирическим распределениями отвергается.

§ Если χ 2 2 _st. То нулевая гипотеза об отсутствии различия между теоретическим и эмпирическим распределениями принимается.

Число степеней свободы находится по формуле: 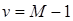, где М – число классов.

Рассмотрим пример: Проверим гипотезу об отсутствии относительной приуроченности вида к какому-либо местообитанию на примере пчелы Megachile rotundata (F.) по 7-летним материалам. М = 5; N = 22905;

Ожидаемое число особей рассчитываем по формуле:

,

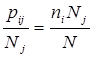
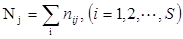
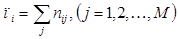
где N_j – число особей S видов в j-ой выборке. , а n_i – общее число особей одного вида во всех выборках М; , а p_ij – доля i-го вида в j-ой выборке.

Оценка различий между ожидаемым и наблюдаемым распределением частот по критерию хи-квадрат

Источник

Понятие о статистической достоверности

Статистическая достоверность имеет существенное значение в расчетной практике ФКС. Ранее было отмечено, что из одной и той же генеральной совокупности может быть избрано множество выборок:

— если они подобраны корректно, то их средние показатели и показатели генеральной совокупности незначительно отличаются друг от друга величиной ошибки репрезентативности с учетом принятой надежности;

— если они избираются из разных генеральных совокупностей, различие между ними оказывается существенным. В статистике по­всеместно рассматривается сравнение выборок;

— если они отличаются несущественно, непринципиально, не­значительно, т. е. фактически принадлежат одной и той же гене­ральной совокупности, различие между ними называется стати­стически недостоверным.

Статистически достоверным различием выборок называется выборка, которая различается значимо и принципиально, т. е. при­надлежит разным генеральным совокупностям.

В ФКС оценка статистической достоверности различий выбо­рок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упраж­нений, тестов, контрольных упражнений связано с их экспери­ментальной проверкой, которая должна показать, что испытуе­мая группа принципиально отлична от контрольной. Поэтому при­меняют специальные статистические методы, называемые крите­риями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками.

Все критерии делятся на две группы: параметрические и непараметрические. Параметрические критерии предусматривают обязательное наличие нормального закона распределения, т.е. имеется в виду обязательное определение основных показателей нормального закона — средней арифметической величины х и среднего квадратического отклонения о. Параметрические крите­рии являются наиболее точными и корректными. Непараметри­ческие критерии основаны на ранговых (порядковых) отличиях между элементами выборок.

Приведем основные критерии статистической достоверности, используемые в практике ФКС: критерий Стьюдента, критерий Фишера, критерий Вилкоксона, критерий Уайта, критерий Ван-дер-Вардена (критерий знаков).

Критерий Стьюдента назван в честь английского ученого К. Госсета (Стьюдент — псевдоним), открывшего данный метод. Критерий Стьюдента является параметрическим, используется для сравнения абсолютных показателей выборок. Выборки могут быть различными по объему.

Критерий Стьюдента определяется так.

1. Находим критерий Стьюдента t по следующей формуле:

где Xi, x₂ — средние арифметические сравниваемых выборок; /я_ь w₂ — ошибки репрезентативности, выявленные на основании показателей сравниваемых выборок.

2. Практика в ФКС показала, что для спортивной работы доста­точно принять надежность счета Р = 0,95.

3. На основании свойств нормального закона распределения в критерии Стьюдента осуществляется сравнение t и t^.

— если t > ftp, то различие между сравниваемыми выборками статистически достоверно;

Дата добавления: 2015-06-17 ; просмотров: 4052 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Понятие о статистической достоверности

Статистическая достоверность имеет существенное значение в расчетной практике ФКС. Ранее было отмечено, что из одной и той же генеральной совокупности может быть избрано множество выборок:

— если они подобраны корректно, то их средние показатели и показатели генеральной совокупности незначительно отличаются друг от друга величиной ошибки репрезентативности с учетом принятой надежности;

— если они избираются из разных генеральных совокупностей, различие между ними оказывается существенным. В статистике по­всеместно рассматривается сравнение выборок;

— если они отличаются несущественно, непринципиально, не­значительно, т. е. фактически принадлежат одной и той же гене­ральной совокупности, различие между ними называется стати­стически недостоверным.

Статистически достоверным различием выборок называется выборка, которая различается значимо и принципиально, т. е. при­надлежит разным генеральным совокупностям.

В ФКС оценка статистической достоверности различий выбо­рок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упраж­нений, тестов, контрольных упражнений связано с их экспери­ментальной проверкой, которая должна показать, что испытуе­мая группа принципиально отлична от контрольной. Поэтому при­меняют специальные статистические методы, называемые крите­риями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками.

Все критерии делятся на две группы: параметрические и непараметрические. Параметрические критерии предусматривают обязательное наличие нормального закона распределения, т.е. имеется в виду обязательное определение основных показателей нормального закона — средней арифметической величины и среднего квадратического отклонения s. Параметрические крите­рии являются наиболее точными и корректными. Непараметри­ческие критерии основаны на ранговых (порядковых) отличиях между элементами выборок.

Приведем основные критерии статистической достоверности, используемые в практике ФКС: критерий Стьюдента и критерий Фишера.

Критерий Стьюдента назван в честь английского ученого К. Госсета (Стьюдент — псевдоним), открывшего данный метод. Критерий Стьюдента является параметрическим, используется для сравнения абсолютных показателей выборок. Выборки могут быть различными по объему.

Критерий Стьюдента определяется так.

1. Находим критерий Стьюдента t по следующей формуле:

где — средние арифметические сравниваемых выборок; т₁, т₂ — ошибки репрезентативности, выявленные на основании показателей сравниваемых выборок.

2. Практика в ФКС показала, что для спортивной работы доста­точно принять надежность счета Р = 0,95.

Для надежности счета: Р = 0,95 (a = 0,05), при числе степеней свободы

3. На основании свойств нормального закона распределения в критерии Стьюдента осуществляется сравнение t и t_гр.

если t t_гр, то различие статистически недостоверно.

Для исследователей в области ФКС оценка статистической до­стоверности является первым шагом в решении конкретной зада­чи: принципиально или непринципиально различаются между собой сравниваемые выборки. Последующий шаг заключается в оценке этого различия с педагогической точки зрения, что опре­деляется условием задачи.

Рассмотрим применение критерия Стьюдента на конкретном примере.

Пример 2.14. Группа испытуемых в количестве 18 человек оценена на ЧСС (уд./мин) до х_i и после y_i разминки.

Оценить эффективность разминки по показателю ЧСС. Исход­ные данные и расчеты представлены в табл. 2.30 и 2.31.

Обработка показателей ЧСС до разминки

Таким образом, до разминки показатели группы составили: ± s_х = (157 ± 3) уд./мин.

Обработка показателей ЧСС после разминки

Таким образом, после разминки показатели группы составили s_y = (169 ± 3) уд./мин.

Теперь определим обе ошибки репрезентативности. Выявля­ется различие между средними показателями и некоей огромной генеральной совокупностью N= которая нам фактически не­известна и из которой избрана первая x_i, а затем вторая y_i вы­борки.

Для определения ошибки используем формулу (2.15), так как число членов генеральной совокупности неизвестно (N = и объем выборки мал (менее 20 элементов). Таким образом,

Ошибки по обеим группам совпали, так как объемы выборок равны (исследуется одна и та же группа при различных условиях), а средние квадратические отклонения составили s_х = s_у = 3 уд./мин. Переходим к определению критерия Стьюдента:

Задаем надежность счета: Р= 0,95.

Статистический вывод. Поскольку t = 11,62, а граничное t_гр = 2,02, то 11,62 > 2,02, т.е. t > t_гр, поэтому различие между выбор­ками статистически достоверно.

Педагогический вывод. Установлено, что по показателю ЧСС раз­личие между состоянием группы до и после разминки является статистически достоверным, т.е. значимым, принципиальным. Итак, по показателю ЧСС можно сделать вывод, что разминка эффективна.

Критерий Фишера является параметрическим. Он применяет­ся при сравнении показателей рассеивания выборок. Это, как пра­вило, означает сравнение по показателям стабильности спортив­ной работы или стабильности функциональных и технических показателей в практике физической культуры и спорта. Выборки могут быть разновеликими.

Критерий Фишера определяется в нижеприведенной последова­тельности.

1. Находим Критерий Фишера F по формуле

где , — дисперсии сравниваемых выборок.

Условиями критерия Фишера предусмотрено, что в числителе формулы F находится большая дисперсия, т.е. число F всегда больше единицы.

По таблице приложения 4 находим граничное значение кри­терия F_гр.

Сравнение критериев F и F_гр позволяет сформулировать вы­воды:

если F > F_гр, то различие между выборками статистически достоверно;

По данным, представленным в таблице приложения 6, находим Fгр: Fгр = 2,4

Обратим внимание на то, что в таблице приложения 6 пере­числение чисел степеней свободы как большей, так и меньшей дисперсии при приближении к большим числам становится гру­бее. Так, числа степеней свободы большей дисперсии следует в таком порядке: 8, 9, 10, 11, 12, 14, 16, 20, 24 и т.д., а меньшей — 28, 29, 30, 40, 50 и т.д.

Это объясняется тем, что при увеличении объема выборок раз­личия F-критерия уменьшаются и можно использовать табличные значения, приближенные к исходным данным. Так, в примере 2.15 =17 отсутствует и можно принять ближайшее к нему значение k = 16, откуда и получаем Fгр = 2,4.

Статистический вывод. Поскольку критерий Фишера F= 2,5 > F= 2,4, выборки различимы статистически достоверно.

Педагогический вывод. Значения времени отталкивания (с) при броске мяча в ворота у гандболистов обеих групп суще­ственно различаются. Эти группы следует рассматривать как раз­личные.

Дальнейшие исследования должны показать, в чем причина такого различия.

Исходные данные и основные расчеты приведены в табл. 2.40 и 2.41.

Обработка показателей времени от подачи сигнала до удара по мячу в начале тренировки

Обработка показателей времени от подачи сигнала до удара по мячу после тренировки

Определим различие групп показателей по критерию Стью­дента:

Определим различие групп показателей по критерию Фишера:

По таблице приложения 2 при надежности Р = 0,95 и степенях свободы k = 22-1=21 значение F_гр = 21. Поскольку F= 1,53 2 Пирсона и критерию трёх сигм»

1. Каждому члену рабочей бригады провести измерение (испытание) своей (личной) быстроты и координированности действий, путём бросания 30-40 раз дротиков в круговую мишень спортивной игры Дартс.

Соответствие быстроты и координированности действий испытуемых нормальному закону распределения

№ п/п										округ- ленно
…
…
Всего

II – й этап исследований

«Оценка средних показателей генеральной совокупности попаданий в мишень спортивной игры Дартс всех студентов учебной группы по результатам измерений членов одной бригады»

Оценить средние показатели быстроты и координированности действий всех студентов учебной группы (согласно списка учебной группы классного журнала) по результатам попаданий в мишень спортивной игры Дартс всех членов бригады, полученным на первом этапе исследований данной лабораторной работы.

Для этого необходимо выполнить следующее.

1. Оформить результаты измерений быстроты и координированности действий при бросании дротиков в круговую мишень спортивной игры Дартс всех членов Вашей бригады (2 – 4 человека), которые представляют собой выборку результатов измерений из генеральной совокупности (результаты измерений всех студентов учебной группы – например, 15 человек), занеся их во второй и третий столбцы таблицы 4.2.

Обработка показателей быстроты и координированности действий

№ п/п
…
…
Всего

2. Выполнить все необходимые расчёты по заполнению таблицы 4.2, а также другие расчёты и выводы, аналогичные расчётам и выводам примера 2.13, приведенным в 2-ом разделе данной методической разработки на страницах 13-14. Следует иметь ввиду, при расчёте ошибки репрезентативности «m» необходимо использовать формулу 2.4, приведенную на странице 13 данной методической разработки, так как выборка мала (n , а число элементов генеральной совокупности N известно, и равно числу студентов учебной группы, согласно списка журнала учебной группы.

III – й этап исследований

Оценка эффективности разминки по показателю «Быстрота и координированность действий» каждым членом бригады с помощью критерия Стьюдента

Для этого необходимо выполнить следующее.

1. Принимая результаты измерений первого этапа исследований за результаты разминки, каждому члену бригады заполнить таблицу 4.3, используя одноимённые графы и строки таблицы 4.1.

Обработка показателя «Быстрота и координированность действий» каждым членом бригады по результатам разминки

№ п/п
…
Всего

2. Произвести вычисления среднего значения дисперсии и СКО , результатов измерений показателя «Быстрота и координированность действий» по результатам разминки, приведенных в таблице 4.3, записать в целом результат измерений по результатам разминки (см. аналогичные расчёты приведенные сразу после таблицы 2.30 примера 2.14 на странице 16 данной методической разработки).

3. Каждому члену рабочей бригады провести измерение (испытание) своей (личной) быстроты и координированности действий после разминки, путём бросания 30-40 раз дротиков в круговую мишень спортивной игры Дартс.

4. Результаты измерений (испытаний) _i (в очках) оформить в виде вариационного ряда и занести в таблицу 4.4 (столбцы , выполнить все необходимые расчёты по заполнению других столбцов этой таблицы.

Обработка показателя «Быстрота и координированность действий» каждым членом бригады после разминки

№ п/п
…
Всего

5. Произвести вычисления среднего значения дисперсии и СКО , результатов измерений показателя «Быстрота и координированность действий» после разминки, приведенных в таблице 4.4, записать в целом результат измерений по результатам разминки (см. аналогичные расчеты, приведенные сразу после таблицы 2.31 примера 2.14 на странице 17 данной методической разработки).

6. Выполнить все необходимые расчёты и выводы, аналогичные расчётам и выводам примера 2.14, приведенным в 2-ом разделе данной методической разработки на страницах 16-17. Следует иметь ввиду, при расчёте ошибки репрезентативности «m» необходимо использовать формулу 2.1, приведенную на странице 12 данной методической разработки, так как выборка n , а число элементов генеральной совокупности N ( неизвестно.

IV – й этап исследований

Оценка однотипности (стабильности) показателей «Быстрота и координированность действий» двух членов бригады с помощью критерия Фишера

Оценить однотипность (стабильность) показателей «Быстрота и координированность действий» двух членов бригады с помощью критерия Фишера, по результатам измерений, полученным на третьем этапе исследований данной лабораторной работы.

Для этого необходимо выполнить следующее.

Используя данные таблиц 4.3 и 4.4, результаты расчётов дисперсий по этим таблицам , полученные на третьем этапе исследований, а также методику расчёта и применения критерия Фишера для оценки однотипности (стабильности) спортивных показателей, приведенную в примере 2.15 на страницах 18-19 данной методической разработки, сделать соответствующие статистический и педагогический выводы.

V – й этап исследований

Оценка групп показателей «Быстрота и координированность действий» одного члена бригады до и после разминки

Источник