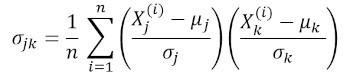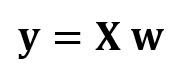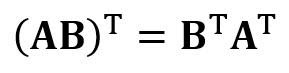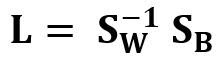какие разделы математики нужны для машинного обучения
Как постичь машинное обучение, если ты не великий математик
Предлагаем почитать перевод статьи Diego Isco с ресурса dev.to. Она будет полезна начинающим специалистам в области ML.
Несколько месяцев назад я изучал проекты, в которых благодаря машинному обучению успешно реализуются невероятные вещи.
И я загорелся этим. Сказал, что хочу этому научиться. Неважно, насколько трудно мне будет. Я хочу научиться, и я научусь.
Будем честны: все мы слышали о зарплатах инженеров по машинному обучению. Взгляните на это.
Впечатляет, правда? Но машинное обучение еще нужно освоить — и вот тут начинается мрак.
Воодушевленный, я начал изучать работы по этой теме, и знаете что? Везде — математика! Навороченные уравнения, линейная алгебра, векторы и странные символы.
В тот вечер я плакал как ребенок. Но, как хороший технарь, утер слезы и решил учиться самостоятельно.
Да, я просто еще один нерд, пытающийся осилить машинное обучение.
Но мне скучно изучать сложные темы. Особенно во время карантина. Поэтому я хочу попробовать что-нибудь другое. Я опишу свой процесс обучения.
Ход обучения
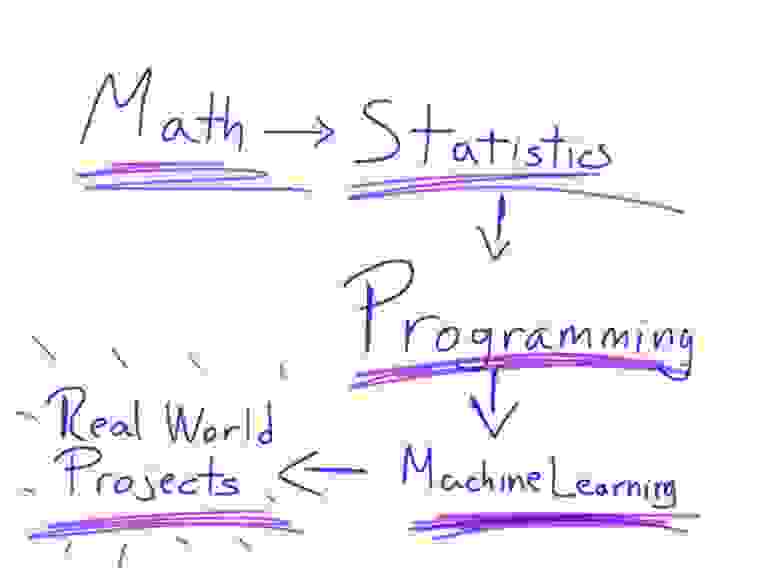
Математика → Статистика → Программирование → Машинное обучение → Любительские проекты
Когда вы будете искать на YouTube видео о машинном обучении, то обязательно наткнетесь на 3 основных — от Siral Raval, Jabril и Daniel Bourke.
Все они — выше всяких похвал. Поэтому я решил взять из этих видео лучшее.
Математика
Много споров по поводу того, насколько хорошо нужно знать математику для освоения машинного обучения. Но знать точно нужно.
Возможно, некоторые из вас чертовски гениальны в математике и вам достаточно вспомнить лишь отдельные вещи. Но большинству простых смертных вроде меня нужно всему учиться с нуля.
Хорошо, а что именно нужно знать? Всего-то линейную алгебру и матанализ.
Напоминаю: я не гений в математике. Я плохо разбираюсь в математике. Я завалил матанализ на всех курсах в университете!
Так вот, можно ли освоить теорию машинного обучения, не будучи гением в математике?
Есть один нюанс. Если вы не дружите с числами, то это потому, что не понимаете основ.
Помните основы? Об основах линейной алгебры и математического анализа рассказывает на канале 3Blue1Brown Грант Сандерсон. Ему надо дать Нобелевскую премию в области образования. Он просто берет математику объясняет ее в потрясающей форме. Как ребенку. Это прекрасно.
Итак, моим первым шагом было понять основы линейной алгебры и математического анализа. Поверьте, после этого все намного проще.
Мы посмотрели и осмыслили эти видео, теперь время применить свои знания на практике — на курсе линейной алгебры от крупнейшего специалиста в сфере преподавания математики — Гилберта Стрэнга из Массачусетского технологического института.
Подумать только: получать такое же образование, что и студенты, заплатившие тысячи долларов за очный курс! Да, диплома одного из лучших университетов мира не будет, но накопленные знания — вот что в итоге имеет значение.
Что ж, мы усвоили этот длинный курс и попрактиковались, теперь черед математического анализа. В Академии Хана есть потрясающая программа, которая дает все, что надо для того, чтобы чувствовать себя уверенно, имея дело с мудреными уравнениями.
Статистика
Многих людей сбивает с толку то, насколько машинное обучение похоже на статистику. На самом деле они тесно связаны друг с другом, так что статистика — ключ к пониманию теории машинного обучения.
Поэтому сосредоточьтесь и учитесь.
А для облегчения этой задачи — бесплатный курс Probability — The Science of Uncertainty and Data от Массачусетского технологического института.
Читая учебную программу, вы можете подумать, что курс базовый, но это не так. Он охватывает достаточно тем, чтобы дать основы для понимания теории вероятности. Всем, кто любит поучиться, вот еще один курс — Statistics and Probability от Академии Хана. Это в дополнение, так что расслабьтесь.
Программирование
Если вы, как и я, инженер-программист, то для вас сейчас будет самое интересное.
Язык программирования, который необходимо знать, это Python. Король машинного обучения. Его простота делает процесс освоения материала очень легким — по крайней мере, поначалу.
Я предполагаю, что вы знаете программирование, так что не хочу пересказывать содержание курсов для изучения Python — их много. Кроме того, есть отличные книги. Вам решать, где набраться знаний.
Кому-то может быть удобнее изучать документацию или пользоваться подпиской на учебную онлайн-платформу, а у кого-то есть любимый учитель на Udemy. Главное, не забывайте практиковаться, чтобы лучше понимать, что происходит при программировании для машинного обучения.
Ладно, допустим, вы не знаете программирования, и это будет ваша первая строчка кода. В таком случае я бы выбрал Datacamp. Смело исследуйте тему самостоятельно и смотрите их курс по Python.
Машинное обучение
Мы уже далеко продвинулись. Изучили математику, статистику, алгоритмы, проплакали несколько ночей. Все ради этого момента.
Курс по машинному обучению от Эндрю Ына — наверное, один из лучших по теме. Он не для новичков, так что не убирайте далеко свои конспекты. Наконец то, как работают алгоритмы машинного обучения, сложится для вас в цельную картинку.
Еще один ресурс — это Introduction to Machine Learning for Coders. Хороший курс с детальными объяснениями алгоритмов машинного обучения.
Советую пройти оба, изучить вопрос с разных сторон, тогда вы сможете сказать, какой курс оказался наиболее понятным.
Не могу не упомянуть еще одну программу, которую очень хвалят. Но она платная: это Introduction to Machine Learning Course нa Udacity. Если у вас отложено немного денег и вы готовы инвестировать в себя, то это подходящий случай, но решайте сами.
Любительские проекты
Теперь вы уже знаете машинное обучение, но этого недостаточно. Вам нужно больше практики. Здесь вам поможет книга Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow.
После этого можно браться за любительские проекты, но уже с лучшими библиотеками машинного обучения. Если вам, как и мне, не нравится опираться на библиотеки без понимания, что к чему, то не волнуйтесь: вы уже разбираетесь. Поэтому я даю эту книгу в самом конце.
И напоследок
Прежде чем завершить, хочу дать несколько советов.
Роль математики в машинном обучении
«Так ли необходимо разбираться в математике, лежащей в основе алгоритмов машинного обучения? В Python ведь уже есть масса широко доступных библиотек, которые можно без труда использовать для построения моделей!»
Я слышал это от дата-сайентистов любителей не один раз. Это заблуждение распространено куда больше, чем хотелось бы, и продолжает порождать наивные фантазии среди начинающих профессионалов в области обработки данных.
Итак, как же нам этому научиться? Что ж, именно об этом я и хочу поговорить с вами сегодня. В этой статье приведены различные аспекты математики, которые вам нужно знать, чтобы в полной мере освоить машинное обучение, включая линейную алгебру, теорию вероятности и многое другое.
На каком уровне нужно разбираться в математике чтобы быть компетентным в машинном обучении?
(Важность математических дисциплин в машинном обучении:
Разница между математическими концепциями, лежащими в основе машинного обучения и Data Science
Хотя Data Science и машинное обучение имеют много общего, все же существуют небольшие различия в их мат-аппаратах. Разница показана на приведенной ниже лепестковой диаграмме:
Да, Data Science и машинное обучение во многом пересекаются, но их основная направленность существенно различается.
Это набор способов выявления скрытых фактов в данных, которые могут быть упущены с первого взгляда. В результате, для сравнения и проверки гипотез, мы должны в большей степени полагаться на концепции статистики и вероятности.
С другой стороны, машинное обучение больше фокусируется на концепциях линейной алгебры, поскольку она служит плацдармом для всех сложных процессов (помимо аспекта эффективности). А также на многомерном исчислении, которое имеет дело с аспектом численной оптимизации, которая является движущей силой большинства алгоритмов машинного обучения.
Тактика сближения с бывшим противником
Если вы будете повторять то же самое, что делали в прошлом, вы получите те же результаты, что и раньше. Я перефразировал знаменитую цитату Альберта Эйнштейна, но я уверен, что вы уловили суть! Многие начинающие энтузиасты машинного обучения совершают эту ошибку, используя тот же подход, что они использовали в прошлом.
Итак, как же вам следует подойти к изучению математики, стоящей за алгоритмами машинного обучения?
Математика в Data Science и машинном обучении связана не с операциями над числами, а с тем, что происходит, почему это происходит и как мы можем поэкспериментировать с разными вещами, чтобы получить желаемые результаты.
Давайте посмотрим на график, показанный ниже, и попробуем вычислить его градиент.
Нам следует уделять больше внимания геометрической интерпретации любого подобного выражения. Это помогает нам интерпретировать значение этих замысловатых выражений. Вся кропотливая работа по ручному решению таких задач не является существенной и не требует навыков. Использование вычислительных библиотек, таких как NumPy, имеет гораздо больший смысл, чем проверка вашей выносливости.
Теперь давайте немного сместим наше внимание, чтобы понять, почему нам нужно изучать эти различные математические методы и что послужило бы хорошим источником для быстрого их изучения.
Линейная алгебра для машинного обучения
Некоторые люди считают линейную алгебру математикой 21 века. Причина в том, что линейная алгебра является основой машинного обучения и Data Science, которые в ближайшие годы совершат революцию во всех остальных отраслях.
Но почему именно линейная алгебра?
Линейная алгебра дает нам систематизированный базис для представления систем линейных уравнений.
Давайте решим это уравнение относительно x и y:
В результате переменная x исключается, а y получается равным 9. При обратной подстановке мы получаем значение x равное 0.
Проблема здесь в том, что для работы этого алгоритма требуется человеческая интуиция. Наши машины не способны имитировать ту же интуицию. Они могут понимать данные только в определенном представлении, а правила в заданном формате.
Наборы данных часто содержат сотни и тысячи наблюдений (даже миллионы). Как вы думаете, сможем ли мы работать с такими наборами данных и вручную находить оптимальные значения x и y?
Конечно нет! Мы определенно предпочли бы автоматизировать эту задачу. И здесь в игру вступает линейная алгебра. В широком смысле:
Это алгебраическое представление задачи, которую мы решили выше. Используя матричные операции, мы можем найти значения x и y в мгновение ока. Это основная причина, по которой линейная алгебра необходима в Data Science и машинном обучении.
Многомерное исчисление для машинного обучения
Какова роль многомерного исчисления в машинном обучении?
Многомерное исчисление, или частная производная, если быть точнее, используются для математической оптимизации заданной функции.
Рассмотрим случай градиентного спуска. Мы знаем, что функция стоимости градиентного спуска задается таким образом:
И мы вычисляем производные по наклону (m) и точке пересечения (c) таким образом:
Но почему только частная производная? Мы могли бы вычислить интеграл или совершить другую операцию. Это связано с тем, что производная показывает нам скорость изменения функции стоимости по отношению к стоимости 丁 по отношению к m и c по отдельности.
Эти отдельные частные производные могут быть представлены в векторной форме.
Это алгебраическое векторное представление частных производных.—=-
Это представление называется Якобианом.
Теория вероятности для машинного обучения
Мы вычисляем ответы, подставляя числа. Но что на самом деле говорит нам теорема Байеса, что именно означает апостериорная вероятность? Почему мы вообще ее рассчитываем?
Давайте рассмотрим пример (Успокойтесь! На это раз без математики!):
Это наш друг Боб. Как его одноклассник, мы думаем, что он интроверт, который зачастую замкнут. Мы считаем, что он не любит заводить друзей.
Итак, P(A) называется априорной вероятностью. В данном случае это будет нашим предположением, что Боб редко любит заводить новых друзей.
Теперь, Боб встречает Эрика в своем колледже.
Их дружба представляет собой P (B|A):
Теперь, глядя на правую часть и на приведенный выше пример, числитель представляет вероятность того, что Боб был дружелюбен P(A) и стал другом Эрика P (B|A). И все эти значения вычисляются по отношению к результату в левой части, а именно:
Однако что это новое значение представляет?
Если бы я извлек весь сок из этого примера, это выглядело бы примерно так:
Мы сделали предположение о Бобе, и обнаруженные нами сведения заключались в том, что он действительно завел нового друга!
Наивный Байесовский алгоритм работает по схожему принципу, с простым предположением, что все входные функции независимы. Чтобы пронаблюдать это явление, нам нужно погрузиться в байесовские сети или вероятностные графические модели.
Статистика для машинного обучения
Статистика составляет основу машинного обучения. Когда мы говорим о статистике, нам в голову приходят несколько знакомых концепций:
Проверка гипотез и т. д.
Большинство из этого играет важную роль в производительности наших моделей машинного обучения, таких как линейная и логистическая регрессия.
Заключение:
Дорожная карта математических дисциплин для машинного обучения, часть 1
Вместо предисловия
Допустим, сидя вечерком в теплом кресле вам вдруг пришла в голову шальная мысль: «Хм, а почему бы мне вместо случайного подбора гиперпараметров модели не узнать, а почему оно всё работает?»
Это скользкий путь — вы думаете, что достаточно пары вечеров с неторопливым чтением главки «Глубокого обучения» или 5-минутных youtube-роликов с различных MOOC; на деле, чтобы создать понимание, а не его иллюзию, требуется приличное количество времени (ну уж никак не меньше полугода для самых фанатичных); но самое печальное — профит от этого мероприятия не очевиден — к счастью (или к сожалению), мир не устроен по законам математики, и будь вы трижды доктором физмат наук — некоторые модели всё равно будут работать лучше только в том случае, если вы подкинете в них побольше предобработанных данных либо соорудите огромный ансамбль.
Я считаю своим долгом вас предупредить, что это кривая дорожка, и возможно, что вложения в математику окупятся не так скоро, как того бы хотелось. Но математика интересна сама по себе, безотносительно приложений. Тем более что если вас заинтересовало, а что же происходит в этом черном ящике с гиперпараметрами, то это означает, что математика вам, скорее всего, не безразлична.
Ещё кое-что про мои рекомендации: я не люблю математическую литературу, которая кишит индексами, перлами типа «a_ijk с тремя подчеркиваниями и шляпкой сопряженное». Я считаю, что идеи важнее строгих выводов. При этом идеи не должны скатываться до «рукомаханий», всё должно быть довольно строго. Я не люблю книги наподобие Бурбаки и Кнута. На мой взгляд, эти книги предназначены для чего угодно, но не для чтения и не для изучения предмета. Они хороши в качестве ссылок и как энциклопедии.
Напоследок приведу кое-что из Бертрана Рассела:
Евклид презирал практическую полезность, которую внедрял Платон. Говорят, что один ученик, прослушав доказательства, спросил, что выиграет он изучением геометрии; тогда Евклид позвал раба и сказал: «Дай молодому человеку грош, поскольку он непременно должен извлекать выгоду из того, что изучает».
Теперь перейду собственно к основной части.
Пререквизиты
Уровни сложности
Не секрет, что по каждой математической дисциплине написано много литературы, и иногда проблемой становится даже простой выбор нужной книги. Я буду выделять несколько уровней сложности в литературе, что вы знали, куда стоит соваться, а куда лезть (пока что) не надо (или к чему можно обратиться для более полной информации).
Дорожная карта
Перейду собственно к конкретным курсам.
Анализ, он же calculus
В российских вузах его преподают довольно интересно: большинство через несколько лет после окончания курса помнят смутно лишь какие-то там интегралы, и кажется что-то ещё. И это при том, что анализ — дисциплина прямо-таки одна из основополагающих в математике вообще. Мостиков от теории к практике как правило нет, и этот курс, подобно летающему острову парит где-то в головах, абсолютно оторванный от реальной жизни. Преодолевать это надо решением задач, причем не только из области математики, но и желательно что-либо из «реальной жизни».
Что нужно знать из анализа?
Основные вещи, которые нам понадобятся — понятие предела, непрерывности, производной, функции многих переменных, градиента, интеграла, интеграла с переменным верхним пределом, многомерного интеграла*.
Литература
Bring it on: тут всё более-менее стандартно — Пискунов / Фихтенгольц.
Hurt me plenty: Зорич, том 1. Эту книгу я люблю очень-очень сильно; это не учебник, но роман в формулах, что-то наподобие Евгения Онегина. К сожалению, он сложнее стандартных курсов по анализу за счет того, что многие вещи в нём даются более общО, и к этому надо привыкнуть; зато за счёт этой общности связываются воедино многие разрозненные вещи (см. те же пределы по базе).
Nightmare: Зорич том1 + том2, Рудин «Основы математического анализа», Львовский «Лекции по математическому анализу», Ramanan «Global Calculus».
В общем и целом резюме тут такое: литературы по анализу даже на русском языке полно; учебники чаще тяготеют к чисто математическим. В качестве дополнения к учебникам уровня 2-3 могу посоветовать несколько курсов:
Практика
Практиковаться и применять полученные знания не то что «опционально», но строго-настрого ОБЯЗАТЕЛЬНО, иначе вся теория повиснет на вас мёртвым грузом, и вы быстро пойдете ко дну, причем даже не осознавая этого.
Предлагаю рассмотреть следующие варианты: Демидович, problem sets с курсов MIT (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Линейная алгебра
Хлеб насущный для Data Science и вообще для науки в целом. К сожалению, люди научились хорошо решать только линейные уравнения и их системы; для уравнений степени 2 и выше существуют всяческие очень нетривиальные теории (коммутативная алгебра, алгебраическая геометрия и иже с ними). Поэтому в анализе данных в основном применяются линейные модели (либо обобщенные линейные модели, как логистические регрессии, перцептроны и т.д.).
На русском языке много книг по линейной алгебре. Проблема в том, что они написаны либо для математиков, либо в них удручающе много индексов (и за деревьями не видно леса). Часто акцент в университетских курсах делается на жордановой форме; про другие стандартные формы часто не упоминается; есть Гаусс и бестолковый Крамер, но редко что бывает про LU, про SVD.
Что нужно знать из линейной алгебры?
Понятие вектора и векторного пространства; понятие линейного оператора; связь операторов и матриц; матричные разложения (LU, SVD как минимум); собственные вектора и собственные значения; ортогональные, унитарные операторы; симметричные и эрмитовы операторы; квадратичные формы, приведение к главным осям.
Литература
Самое хорошее в этом курсе — отсутствие «сложных» и довольно бестолковых теорем линейной алгебры, всяческих двойственных пространств, большое количество задач в книге, практико-ориентированный подход (не «что это такое», а «как это посчитать»). Более толковых курсов по линейной алгебре я ещё не встречал.
Hurt me plenty: Axler «Linear algebra done right»; Гельфанд «Лекции по линейной алгебре»; курс МФТИ lectoriy.mipt.ru/course/LinearAlgebra; Кострикин «Введение в алгебру, часть 2», Тыртышников «Матричный анализ и линейная алгебра».
Проблема книг и курсов с этого уровня сложности в том, что они теоретико-ориентированные. Есть линейные функционалы и двойственные пространства, но нет матрицы проекции на подпространство и практических способов вычисления собственных значений. Скорее всего, курсы с этого уровня придётся дополнять сильной практикой; к примеру, численными методами линейной алгебры.
Про последнюю книгу отдельно. На мой взгляд, это одна из самых удачных русскоязычных книг по линейной алгебре в том смысле, что она не очень сильно оторвана от практики; при этом в ней содержатся и всяческие «продвинутые» темы. Она в какой-то мере может заменить лекции Стрэнга полностью, но её надо дополнять простыми задачами на «набить руку». Задачки в этой книге есть, но они довольно суровые.
Nightmare: Кострикин-Манин «Линейная алгебра и геометрия», Шафаревич-Ремизов «Линейная алгебра и геометрия».
В целом, на русском есть много хорошей литературы, особенно на последнем уровне, но она страдает излишней сложностью.
Практика
Как и в первом случае, практика обязательна. Проходите SVD — изучите сжатие изображений. Проходите матричные умножения — изучите быстрое преобразование Фурье, алгоритм Штрассена; решайте много задач (например, из задачников Кострикина либо Проскурякова); напишите своё LU-разложение, Гаусса. Для самых упорных я могу предложить замечательные книги по численным методам линейной алгебры, такие как Trefethen, Bau «NUMERICAL LINEAR ALGEBRA»; Хорн, Джонсон «Матричный анализ». Эти книги будут полезны, во первых, для «набития» руки; во-вторых, станет сразу понятно, что многие теоретические методы разбиваются в щепки о прозу жизни (машинная точность, нестабильность методов, работа с разреженными матрицами).
Дискретная математика
Ещё один кит современной CS. Здесь нас в основном будет интересовать комбинаторика и основы теории графов.
Что нужно знать из комбинаторики и теории графов?
Биномиальные коэффициенты, их асиптотика; графы; деревья; поиск в глубину и ширину; реккурентные соотношения и их решения;
Литература
Bring it on: Андерсон Дж. «Дискретная математика и комбинаторика»; Хаггарти, Шлипф Дж., Уайтсайдс С. «Дискретная математика для программистов», Оре О. «Графы и их применение».
Две первые книги — прекрасные талмуды по дискретной математике, покрывают практически все вопросы, которые надо знать.
Hurt me plenty: Грэхем, Кнут, Паташник «Конкретная математика», Харари «Теория графов», Оре «Теория графов».
Nightmare: Сачков «Введение в комбинаторные методы дискретной математики», Омельченко «Теория графов».
Линейная алгебра для Data Science и Machine Learning
Линейная алгебра в Data Science и Machine Learning является основополагающей. Новички, начинающие свой путь обучения в области Data Science, а также признанные практики должны развить хорошее понимание основных понятий линейной алгебры.
Специально к новому старту курса математика и Machine Learning для Data Science делимся переводом статьи Бенджамина Оби Тайо — физика, кандидата наук и преподавателя Data Science — о том, что нужно знать, чтобы лучше понимать Data Science и Machine Learning.
Линейная алгебра — это раздел математики, который чрезвычайно полезен в Data Science и машинном обучении. Владение линейной алгеброй — это также самый важный математический навык в машинном обучении. Большинство моделей машинного обучения могут быть выражены в матричном виде. Сам набор данных часто представляется в виде матрицы. Линейная алгебра используется при предварительной обработке данных, в преобразовании данных и оценке моделей. Вот темы, с которыми вы должны быть знакомы:
В этой статье мы проиллюстрируем применение линейной алгебры в Data Science и Machine Learning с использованием набора данных рынка технологических акций, который можно найти здесь.
Линейная алгебра для предварительной обработки данных
Мы начнём с иллюстрации того, как линейная алгебра применяется для предварительной обработки данных.
Импорт необходимых библиотек линейной алгебры
Чтение набора данных и отображение признаков
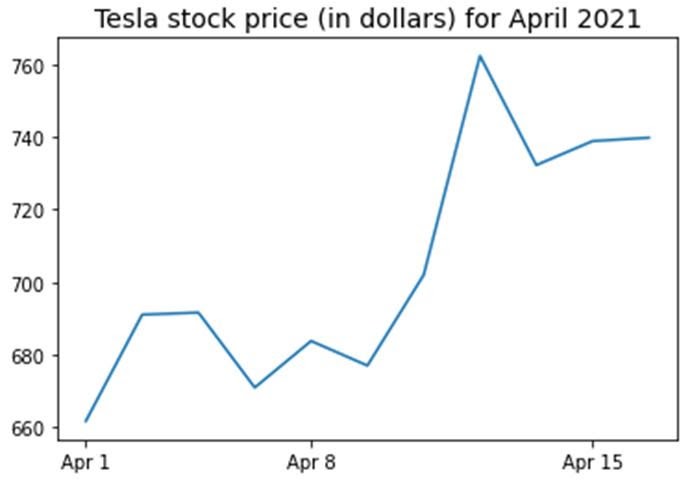
Функция data.shape позволяет нам узнать размерность нашего набора данных. В этом случае набор данных содержит 5 признаков (date, AAPL, TSLA, GOOGL и AMZN) и каждый содержит 11 наблюдений. Дата (date) относится к торговым дням в апреле 2021 года (до 16 апреля). AAPL, TSLA, GOOGL и AMZN — это цены закрытия акций Apple, Tesla, Google и Amazon соответственно.
Визуализация данных
Чтобы выполнить визуализацию данных, нужно определить столбцовые матрицы визуализируемых признаков:
Ковариационная матрица
Ковариационная матрица является одной из наиболее важных матриц в Data Science и Machine Learning. Она предоставляет информацию о совместном движении (корреляции) между признаками. Предположим, у нас есть матрица признаков с 4 признаками и n наблюдениями, как показано в таблице 2:

Чтобы визуализировать корреляции между признаками, мы можем сгенерировать диаграмму рассеяния:

где μ и σ — среднее значение и стандартное отклонения признака соответственно. Это уравнение указывает, что при нормализации признаков матрица ковариации представляет собой просто точечное произведение между признаками. Ковариационная матрица может быть выражена в виде вещественной и симметричной матрицы 4 х 4:
Эта матрица может быть преобразована в диагональную путём выполнения унитарного преобразования, также называемого преобразованием анализа главных компонентов (PCA), чтобы получить следующее:
Поскольку след матрицы при унитарном преобразовании остаётся инвариантным, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X1, X2, X3 и X4.
Вычисление ковариационной матрицы для технологических акций
Обратите внимание, что при этом используется транспонирование нормализованной матрицы.
Визуализация ковариационной матрицы
Из рисунка 3 видно, что AAPL сильно коррелирует с GOOGL и AMZN и слабо с TSLA. TSLA обычно слабо коррелирует с AAPL, GOOGL и AMZN, в то время как AAPL, GOOGL и AMZN сильно коррелируют друг с другом.
Вычисление собственных значений ковариационной матрицы
Мы наблюдаем, что, как и ожидалось, след ковариационной матрицы равен сумме собственных значений.
Вычисление кумулятивной дисперсии
Поскольку след матрицы остаётся инвариантным при унитарном преобразовании, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X1, X2, X3 и X4. Следовательно, мы можем определить следующие величины:

Обратите внимание, что когда p = 4, кумулятивная дисперсия, как и ожидалось, становится равной 1.
Из кумулятивной дисперсии (cum_var) мы видим, что 85 % дисперсии содержатся в первом собственном значении и 11 % — во втором. Это означает, что при реализации PCA могут использоваться только первые два основных компонента, поскольку 97 % общей дисперсии приходятся на эти 2 компонента. Это может существенно уменьшить размерность пространства признаков (с 4 до 2), когда реализован PCA.
Матрица линейной регрессии
Предположим, у нас есть набор данных, который имеет 4 признака предиктора и n наблюдений, как показано ниже.
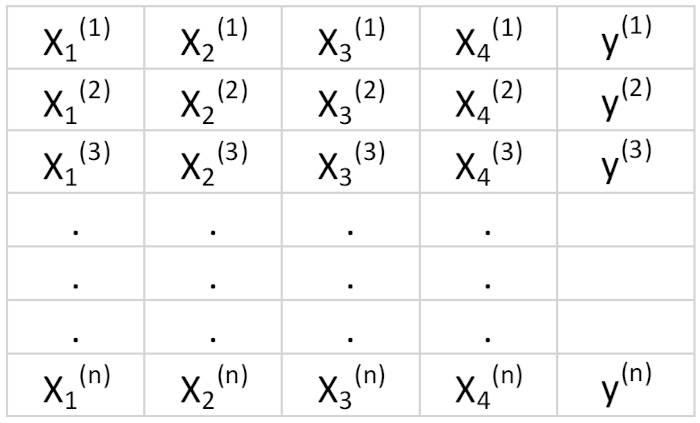
Мы хотели бы построить модель множественной регрессии для прогнозирования значений y (столбец 5). Таким образом, наша модель может быть выражена так:
В матричном виде это уравнение можно записать так:
где X — матрица признаков (n x 4), w — матрица (4 x 1), представляющая определяемые коэффициенты регрессии, и y — матрица (n x 1), содержащая n наблюдений целевой переменной y.
Обратите внимание, что X является прямоугольной матрицей, поэтому мы не можем решить приведённое выше уравнение, взяв обратную X величину.
Чтобы преобразовать X в квадратную матрицу, мы умножаем левую и правую части нашего уравнения на транспонирование из X, то есть:
Это уравнение можно записать так:
является матрицей регрессии (4×4). Мы наблюдаем, что R — это вещественная и симметричная матрица. Обратите внимание, что в линейной алгебре транспонирование произведения двух матриц подчиняется следующему соотношению:
Теперь, когда мы сократили нашу задачу регрессии и выразили её в терминах (4×4) вещественной, симметричной и обратимой матрицы регрессии R, легко показать, что точное решение уравнения регрессии выглядит так:
Примеры регрессионного анализа для прогнозирования непрерывных и дискретных переменных приведены ниже:
Основы линейной регрессии для абсолютных новичков.
Построение перцептронного классификатора с помощью метода наименьших квадратов.
Матрица линейного дискриминантного анализа
Другим примером реальной и симметричной матрицы в Data Science является матрица линейного дискриминантного анализа (LDA). Эта матрица может быть выражена так:
Где SW — матрица рассеяния в пределах признака (the within-feature scatter matrix), а SB — матрица рассеяния между признаками. Поскольку обе матрицы SW и SB вещественны и симметричны, из этого следует, что L также вещественна и симметрична. Диагонализация L создаёт подпространство признаков, которое оптимизирует раздельность классов и уменьшает размерность. Следовательно, LDA является алгоритмом обучения с учителем, а PCA — нет.
Чтобы узнать больше о реализации LDA, пожалуйста, ознакомьтесь со следующими ссылками:
Машинное обучение: уменьшение размерности с помощью линейного дискриминантного анализа.
Репозиторий GitHub для реализации LDA с использованием набора данных Iris.
Машинное обучение Python от Себастьяна Рашки, 3-е изд. (глава 5).
Резюме
Итак, мы обсудили несколько применений линейной алгебры в Data Science и машинном обучении. Используя набор данных рынка технологических акций, мы проиллюстрировали важные понятия, такие как размер матрицы, столбцовые матрицы, квадратные матрицы, ковариационные матрицы, транспонирование матрицы, собственные значения, точечные произведения и т. д.
Линейная алгебра является важным инструментом в Data Science и машинном обучении. Таким образом, новички, интересующиеся Data Science, должны ознакомиться с основными понятиями линейной алгебры.
Чтобы в деталях разобраться с внутренней механикой Data Science, не оставив без внимания машинное обучение, вы можете присмотреться к нашему курсу математика и Machine Learning для Data Science, где опытные менторы и эксперты в своём деле ответят на сложные вопросы, устранят неясности и правильно направят ваши размышления, чтобы в дальнейшем вы решали сложные проблемы самостоятельно.
Узнайте, как прокачаться и в других специальностях или освоить их с нуля: