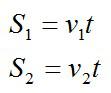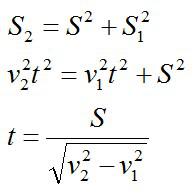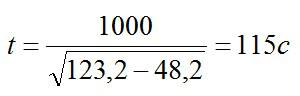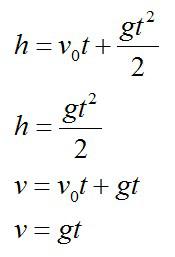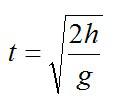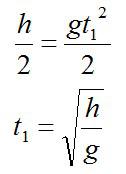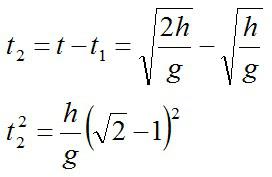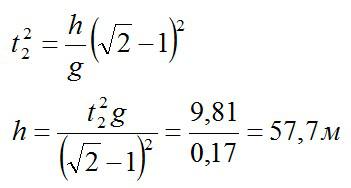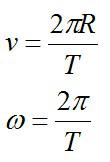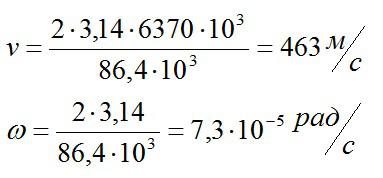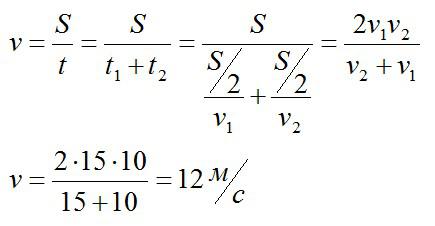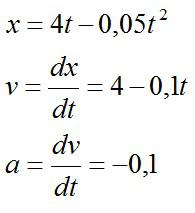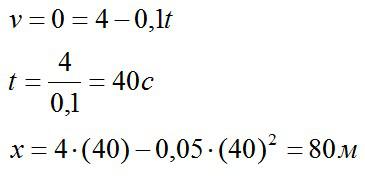кинематика задания для тренировки

Кинематика задания для тренировки

Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время а такой же последний — за время Найдите полное время падения тела t, если его начальная скорость равна нулю.

Нарисуем схематично рисунок (в принципе, он не обязателен)

Если t — полное время падения с высоты H, то

Ответ:

Примечание: поскольку общее время получилось меньше, чем сумма времен на участках и (), заключаем, что эти участки «перекрывались». Таким образом, рисунок, в большей степени соответствующий реальности, должен выглядеть следующим образом:

Однако, как и отмечается в самом начале, конкретный вид рисунка не имеет никакого значения, он только помогает написать правильное уравнение.

Как такое возможно?! Пусть, время полёта=1.25с. Следовательно, S=gt^2/2=7,8125. Что меньше 10-ти. А из условия известно, что 1 участок пути=2 участку пути=10 м.(потому что тело свободно падает) Поэтому, из условия мы знаем, что S>10, что не соответствует ответу.

Участки накладываются друг на друга. Их общий путь меньше суммы.

Потому что

Эту задачу можно решить ещё одним способом.

1.находим скорость тела в конце первого участка Vk1=g*t=10*1=10 м/с.

2. Находим начальную скорость при входе в последний участок

10=V02 + (5/4) => V02=8,75 m/c

Сравниваем скорости Vk1>V02 => 10>8,75.

Значит участки перекрываются (см. чертёж).

Значит надо из суммарного времени полёта по условию задачи вычесть двойное время пролёта участка перекрытия. Это время легко найти зная скорость V02 и Vk1

Vk1=V02+g*t => 10=8,75 +10*t => t=0,125 сек

Окончательно получаем время Полёта:

Тело, свободно падающее с некоторой высоты из состояния покоя, за время после начала движения проходит путь в раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

Рисунок не обязателен

Если t — полное время падения с высоты H, то

Ответ:

Критерии оценки выполнения задания

Приведено полное правильное решение, включающее следующие элементы:

— правильно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом (в данном случае — уравнение кинематики свободно падающего тела);

— проведены необходимые математические преобразования, приводящие к правильному числовому ответу, и представлен ответ.

— Представлено правильное решение только в общем виде, без каких-либо числовых расчетов.

— Правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу.

— В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу.

— В решении содержится ошибка в необходимых математических преобразованиях и отсутствуют какие-либо числовые расчеты.

— Записаны все исходные формулы, необходимые для решения задачи, но в ОДНОЙ из них допущена ошибка.

— Отсутствует одна из формул, необходимых для решения задачи.

Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т. п.).

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Кинематические уравнения движения шарика имеют вид:

В момент второго соударения шарика с плоскостью откуда

Решая систему уравнений, получаем:

и

Из рисунка видно, что

Ответ:

Почему угол отражения и падения равен альфа?

В этой задаче движение тела рассматривается в «наклоненной» системе координат. В ней вдоль обеих осей тело двигается с постоянным ускорением (так как теперь ускорение свободного падения имеет проекции на обе оси). Здесь выписаны обычные уравнения зависимости координаты от времени при равноускоренном движении:

.

Смотрите, при решении задачи, оси, на которые Вы будете что-то проектировать, Вы выбираете сами, из принципа удобства. Даже если тело движется вдоль одной прямой, можно описывать его движение при помощи двух осей, и будет оно там двигаться вдоль какой-то прямой . Но так делать неудобно, лишняя морока, поэтому всегда ось выбирается вдоль направления движения. Тут тело движется уже по параболе, его ускорение направлено вниз. Можно решить эту задачу при помощи любых двух осей, не обязательно даже взаимно перпендикулярных, подойдут и обычные оси: вертикальная и горизонтальная. Но оказывается, что наиболее удобно решать такие задачи в осях вдоль и поперек наклонной плоскости. Тут осложняется тем, что по обеим осям получается ускоренное движение, но сами уравнения решать проще, чем в стандартных осях, где по горизонтальной оси движение равномерное, а по вертикальной — ускоренное.

не написано, потому что начало координат было расположено в место отскока.

а почему у Х есть ускорение? разве оно не равно 0?

Ось Х теперь не направлена горизонтально, поэтому есть ненулевая проекция ускорения на эту ось. Смотрите ответы на комментарии выше.

Почему в проекции на ось Х начальная скорость умножается на синус, а не косинус??

Потому что угол откладывается от оси Oy, а не от оси Ox, как обычно

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью под углом к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Выбор системы координат: ось x направлена по прямой AB, ось y — вверх по наклонной плоскости перпендикулярно линии AB.

Проекции вектора ускорения свободного падения :

Движение по наклонной плоскости эквивалентно движению тела, брошенного под углом к горизонту, в поле тяжести с ускорением

Уравнения движения вдоль осей x и y:

В момент времени t, соответствующий концу движения, и Используя это условие для решения системы уравнений, получаем

Ответ:

Приведенное решение не убедительно

Ускорение определяется из второго закона Ньютона по действию всех сил. Почему-то учитывается только сила тяжести, а про реакцию опоры ни слова.

Все верно, но сила реакции опоры направлена перпендикулярно плоскости, а значит она не может давать вклада в проекцию ускорения на эту плоскость. Нас интересует движение в плоскости, поэтому нам достаточно рассмотреть второй закон Ньютона в проекции только на эту плоскость. Более того, раз тело двигается по плоскости, составляющая ускорения, перпендикулярная плоскости обращается в ноль.

Если ее решить как

Ответе, пожалуйста. Данная задача была сегодня на ЕГЭ.

Если её ре­шить так, то

Тело если просто бросить под углом 60, то оно бы пролетело 0,346 метров. А у Вас получается больше, в случае, когда тело бросают ещё под углом.

Эффективное ускорение свободного падения вдоль наклонной плоскости вдвое меньше поэтому дальность полёта вдвое больше. Шайба как будто находится в меньшем поле тяжести, чем на Земле.

Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние Исходя из этих данных, школьник определил скорость самолета. Чему она оказалась равна?

Поскольку угол наклона глиссады мал, то в момент максимального сближения самолета и школьника расстояние между ними примерно равно

где l — раcстояние до глиссады.

Звук от двигателей, излученный в этот момент, доходит до школьника, согласно условию, спустя время и школьник слышит максимум громкости.

За время самолёт успевает удалиться от точки максимального сближения со школьником в направлении перпендикулярном на расстояние, равное Таким образом, и скорость самолета

Источник

Задачи по кинематике с решениями

В нашей сегодняшней статье мы разберем по одной задаче из каждого подраздела кинематики.

Надоело грызть гранит науки и хочется полезной и легкой для восприятия информации? Добро пожаловать в наш телеграм! Здесь вас ждет ежедневная и разнообразная рассылка.

Примеры решения задач по разным разделам кинематики

Давайте вспомним, какие темы мы уже рассматривали в рубрике «Физика для чайников»:

Задачи по кинематике с решениями

Задача №1. Относительность движения

Условие

Теплоход движется по озеру параллельно берегу со скоростью v1 = 25 км/ч. От берега отходит катер со скоростью v2 = 40 км/ч. Через какое наименьшее время катер сможет догнать теплоход, если в начальный момент теплоход и катер находились на одной нормали к берегу и расстояние между ними было S = 1 км?

Решение

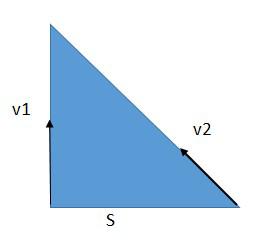
t – искомое наименьшее время. Катер может двигаться по самым разным траекториям, но для того, чтобы догнать теплоход за наименьшее время с максимальнойскоростью, катеру нужно плыть по прямой в некоторую точку, в которую теплоход приплывет одновременно с прибытием туда катера. В таком случае траектории теплохода и катера образуют прямоугольный треугольник вместе с отрезком, соединяющим их положения в начальный момент времени. Расстояния, пройденные соответственно теплоходом и катером до момента встречи:

Далее воспользуемся теоремой Пифагора:

Переводим в СИ и подставляем значения

Ответ: 115 секунд.

Задача №2. Свободное падение тел

Условие

Камень, свободно падающий без начальной скорости, пролетел вторую половину пути за 1 секунду. С какой высоты h упал камень?

Решение

Направим ось Y вертикально вниз. За начало координат примем точку, из которой летел камень. Закон движения камня в проекции на ось имеет вид:

Время падения камня:

Для середины пути справедливы соотношения:

Время t2, за которое пройдена вторая половина пути (оно известно по условию), можно вычислить по формуле:

Отсюда находим высоту:

Ответ: 57,7 метров

Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №3. Движение по окружности

Условие

Каковы линейная и угловая скорости точек на экваторе Земли при ее вращении вокруг своей оси?

Решение

Линейную и угловую скорости при движении по окружности можно найти по формулам:

Обратимся к справочнику и найдем радиус Земли: 6370 км. Период обращения – 24 часа или 86400 секунд. Осталось произвести вычисления:

Ответ: 463 метра в секунду; 7,3 на 10 в минус пятой степени радиан в секунду.

Задача №4. Равномерное движение

Условие

Автомобиль проехал два одинаковых участка пути с разными скоростями (v1=15 м/с, v2=10 м/с). Найти среднюю скорость автомобиля.

Решение

Средняя скорость при равномерном прямолинейном движении равна отношению пройденного пути к затраченному времени.

Ответ: 12 метров в секунду.

Задача №5. Равноускоренное движение

Условие

Решение

Подставим значения из условия и запишем закон движения тела, скорость и ускорение найдем соответственно как первую и вторую производные:

В момент, когда скорость равна нулю:

Вопросы по теме «Кинематика»

Вопрос 1. Чем отличается путь от перемещения?

Ответ. Путь – скалярная величина, равная длине траектории. Перемещение – вектор, соединяющий начальную и конечную точки пути.

Вопрос 2. Что изучает кинематика?

Ответ. Кинематика изучает движение тел, величины и связи, характеризующие его. Кинематика не изучает причины, по которым происходит движение.

Вопрос 3. Может ли ускорение быть отрицательным?

Ответ. Ускорение – векторная величина, отрицательной может быть его проекция на координатную ось. Например, если ускорение направлено противоположно скорости, тело будет замедляться.

Вопрос 4. Что такое инерциальная система отсчета?

Ответ. Инерциальная система отсчета – такая система, в которой свободные тела движутся равномерно и прямолинейно (или покоятся), если на них не действуют внешние силы (или действие этих сил скомпенсировано).

Вопрос 5. В чем заключается относительность движения?

Ответ. Положение и перемещение тела в пространстве всегда описывается относительно другого тела (тело отсчета), с которым связана система отсчета и координаты. В зависимости от выбора тела отсчета, движение может описываться по-разному.

Нужна помощь в решении задач по физике или в заданиях любому другому предмету? Обращайтесь в профессиональный студенческий сервис.

Источник

Кинематика задания для тренировки

Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время а такой же последний — за время Найдите полное время падения тела t, если его начальная скорость равна нулю.

Нарисуем схематично рисунок (в принципе, он не обязателен)

Если t — полное время падения с высоты H, то

Ответ:

Примечание: поскольку общее время получилось меньше, чем сумма времен на участках и (), заключаем, что эти участки «перекрывались». Таким образом, рисунок, в большей степени соответствующий реальности, должен выглядеть следующим образом:

Однако, как и отмечается в самом начале, конкретный вид рисунка не имеет никакого значения, он только помогает написать правильное уравнение.

Как такое возможно?! Пусть, время полёта=1.25с. Следовательно, S=gt^2/2=7,8125. Что меньше 10-ти. А из условия известно, что 1 участок пути=2 участку пути=10 м.(потому что тело свободно падает) Поэтому, из условия мы знаем, что S>10, что не соответствует ответу.

Участки накладываются друг на друга. Их общий путь меньше суммы.

Потому что

Эту задачу можно решить ещё одним способом.

1.находим скорость тела в конце первого участка Vk1=g*t=10*1=10 м/с.

2. Находим начальную скорость при входе в последний участок

10=V02 + (5/4) => V02=8,75 m/c

Сравниваем скорости Vk1>V02 => 10>8,75.

Значит участки перекрываются (см. чертёж).

Значит надо из суммарного времени полёта по условию задачи вычесть двойное время пролёта участка перекрытия. Это время легко найти зная скорость V02 и Vk1

Vk1=V02+g*t => 10=8,75 +10*t => t=0,125 сек

Окончательно получаем время Полёта:

Тело, свободно падающее с некоторой высоты из состояния покоя, за время после начала движения проходит путь в раз меньший, чем за такой же промежуток времени в конце движения. Найдите полное время движения.

Рисунок не обязателен

Если t — полное время падения с высоты H, то

Ответ:

Критерии оценки выполнения задания

Приведено полное правильное решение, включающее следующие элементы:

— правильно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом (в данном случае — уравнение кинематики свободно падающего тела);

— проведены необходимые математические преобразования, приводящие к правильному числовому ответу, и представлен ответ.

— Представлено правильное решение только в общем виде, без каких-либо числовых расчетов.

— Правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу.

— В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу.

— В решении содержится ошибка в необходимых математических преобразованиях и отсутствуют какие-либо числовые расчеты.

— Записаны все исходные формулы, необходимые для решения задачи, но в ОДНОЙ из них допущена ошибка.

— Отсутствует одна из формул, необходимых для решения задачи.

Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т. п.).

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен 30°. На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Кинематические уравнения движения шарика имеют вид:

В момент второго соударения шарика с плоскостью откуда

Решая систему уравнений, получаем:

и

Из рисунка видно, что

Ответ:

Почему угол отражения и падения равен альфа?

В этой задаче движение тела рассматривается в «наклоненной» системе координат. В ней вдоль обеих осей тело двигается с постоянным ускорением (так как теперь ускорение свободного падения имеет проекции на обе оси). Здесь выписаны обычные уравнения зависимости координаты от времени при равноускоренном движении:

.

Смотрите, при решении задачи, оси, на которые Вы будете что-то проектировать, Вы выбираете сами, из принципа удобства. Даже если тело движется вдоль одной прямой, можно описывать его движение при помощи двух осей, и будет оно там двигаться вдоль какой-то прямой . Но так делать неудобно, лишняя морока, поэтому всегда ось выбирается вдоль направления движения. Тут тело движется уже по параболе, его ускорение направлено вниз. Можно решить эту задачу при помощи любых двух осей, не обязательно даже взаимно перпендикулярных, подойдут и обычные оси: вертикальная и горизонтальная. Но оказывается, что наиболее удобно решать такие задачи в осях вдоль и поперек наклонной плоскости. Тут осложняется тем, что по обеим осям получается ускоренное движение, но сами уравнения решать проще, чем в стандартных осях, где по горизонтальной оси движение равномерное, а по вертикальной — ускоренное.

не написано, потому что начало координат было расположено в место отскока.

а почему у Х есть ускорение? разве оно не равно 0?

Ось Х теперь не направлена горизонтально, поэтому есть ненулевая проекция ускорения на эту ось. Смотрите ответы на комментарии выше.

Почему в проекции на ось Х начальная скорость умножается на синус, а не косинус??

Потому что угол откладывается от оси Oy, а не от оси Ox, как обычно

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью под углом к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Выбор системы координат: ось x направлена по прямой AB, ось y — вверх по наклонной плоскости перпендикулярно линии AB.

Проекции вектора ускорения свободного падения :

Движение по наклонной плоскости эквивалентно движению тела, брошенного под углом к горизонту, в поле тяжести с ускорением

Уравнения движения вдоль осей x и y:

В момент времени t, соответствующий концу движения, и Используя это условие для решения системы уравнений, получаем

Ответ:

Приведенное решение не убедительно

Ускорение определяется из второго закона Ньютона по действию всех сил. Почему-то учитывается только сила тяжести, а про реакцию опоры ни слова.

Все верно, но сила реакции опоры направлена перпендикулярно плоскости, а значит она не может давать вклада в проекцию ускорения на эту плоскость. Нас интересует движение в плоскости, поэтому нам достаточно рассмотреть второй закон Ньютона в проекции только на эту плоскость. Более того, раз тело двигается по плоскости, составляющая ускорения, перпендикулярная плоскости обращается в ноль.

Если ее решить как

Ответе, пожалуйста. Данная задача была сегодня на ЕГЭ.

Если её ре­шить так, то

Тело если просто бросить под углом 60, то оно бы пролетело 0,346 метров. А у Вас получается больше, в случае, когда тело бросают ещё под углом.

Эффективное ускорение свободного падения вдоль наклонной плоскости вдвое меньше поэтому дальность полёта вдвое больше. Шайба как будто находится в меньшем поле тяжести, чем на Земле.

Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние Исходя из этих данных, школьник определил скорость самолета. Чему она оказалась равна?

Поскольку угол наклона глиссады мал, то в момент максимального сближения самолета и школьника расстояние между ними примерно равно

где l — раcстояние до глиссады.

Звук от двигателей, излученный в этот момент, доходит до школьника, согласно условию, спустя время и школьник слышит максимум громкости.

За время самолёт успевает удалиться от точки максимального сближения со школьником в направлении перпендикулярном на расстояние, равное Таким образом, и скорость самолета

Источник