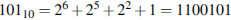кодирование и операции над числами в разных системах счисления

13.07.202215.07.2022 admin 0 Comments

Разбор заданий ЕГЭ: Кодирование и операции над числами в разных системах счисления

Новые аудиокурсы повышения квалификации для педагогов

Слушайте учебный материал в удобное для Вас время в любом месте

откроется в новом окне

Выдаем Удостоверение установленного образца:

«IQ и EQ как основа успешного обучения»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Применение облачных сервисов в педагогической практике учителя (практический курс)

Курс профессиональной переподготовки

Информатика: теория и методика преподавания в образовательной организации

Подготовка к ЕГЭ. Разбор заданий № 1 «Кодирование и операции над числами в разных системах счисления» (раздел Системы счисления).

Используемые материалы:

Для теоретической и практической подготовки к решению заданий применяются ссылки на порталы ЯКласс, «Решу ЕГЭ»; онлайн-тест Константина Полякова.

Номер материала: ДБ-1225279

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Рособрнадзор сообщил о снижении результатов ЕГЭ по естественно-научным предметам

Время чтения: 1 минута

Amazon оплатит своим сотрудникам обучение в вузах

Время чтения: 1 минута

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

В Минпросвещения рассказали о системе оценок по физкультуре в школах

Время чтения: 0 минут

Минобрнауки предлагает дифференцированный подход к аккредитации вузов

Время чтения: 1 минута

ЕГЭ в 2022 году может пройти в допандемийном формате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Кодирование и операции над числами в разных системах счисления

Описание разработки

Задания:

1. Дано А = A7₁₆, B = 251₈. Найдите сумму A + B.

Переведем числа в десятичную систему счисления, выполним сложение, и переведем сумму в двоичную систему счисления:

336₁₀ = 1⋅2 8 + 1⋅2 6 + 1⋅2 4 = 101010000₂.

2. Какое из неравенств выполняется для чисел А = 164₈, В = А3₁₆ и С = 2200₄?

1) A 2 + 6⋅8 1 + 4⋅8 0 = 64 + 48 + 4 = 116₁₀.

В = A3₁₆ = 10⋅16 1 + З⋅16 0 = 163₁₀.

С = 2200₄ = 2⋅4 3 + 2⋅4 2 + 0⋅4 1 + 0⋅4 0 = 2⋅(64 + 16) = 160₁₀.

Задания A1. Кодирование и операции над числами в разных системах счисления

1. Дано А = A7₁₆, B = 251₈. Найдите сумму A + B.

336₁₀ = 1⋅2 8 + 1⋅2 6 + 1⋅2 4 = 101010000₂.

2. Какое из неравенств выполняется для чисел А = 164₈, В = А3₁₆ и С = 2200₄?

Переведем числа в десятичную систему счисления и затем сравним их:

А = 164₈ = 1⋅8 2 + 6⋅8 1 + 4⋅8 0 = 64 + 48 + 4 = 116₁₀.

В = A3₁₆ = 10⋅16 1 + З⋅16 0 = 163₁₀.

С = 2200₄ = 2⋅4 3 + 2⋅4 2 + 0⋅4 1 + 0⋅4 0 = 2⋅(64 + 16) = 160₁₀.

3. Сколько единиц в двоичной записи десятичного числа 127?

Переведем число из десятичной системы счисления в двоичную: нужно делить его на 2, пока делимое не будет меньше 2. После запишем остатки от деления начиная с конца. У нас получится число 1111111. Оно содержит 7 единиц.

4. Как выглядит число В0С₁₆ в двоичной системе счисления?

Для решения этого задания можно пойти одним из двух путей: перевести число В0С из шестнадцатеричной в десятичную, а потом в двоичную, или заменить каждый разряд шестнадцатеричной системы на четыре бита двоичной

5. Двоичным эквивалентом десятичного числа 101 является:

6. Вычислите сумму чисел 5A₁₆ + 50₈. Результат представьте в двоичной системе счисления.

Переведём число 5A₁₆ в двоичную систему счисления: 5A₁₆= 5×16 1 + 10×16 0 = 90₁₀ = 1011010₂.

Переведём число 50₈ в двоичную систему счисления: 50₈ = 5×8 + 0 = 40₁₀ = 101000₂.

Выполним сложение: 1011010₂ + 101000₂ = 10000010₂.

7. Значение выражения 11₁₆ + 11₈ : 11₂ в двоичной системе счисления равно

Переведем все числа в десятичную сисему счисления, выполним действия и переведем результат в двоичную систему счисления:

17 + 9 : 3 = 17 + 3 = 20₁₀,

8. Вычислите сумму чисел х и у при x = B3₁₆, у = 110110₂. Результат представьте в десятичной системе счисления.

Переведём число x в десятичную систему счисления:

Переведём число у в десятичную систему счисления:

110110₂= 1×2 5 + 1×2 4 + 0×2 3 + 1×2 2 + 1×2 1 + 0×2° = 32+ 1б + 4 + 2 = 54₁₀.

Источник

Кодирование и операции над числами в разных системах счисления

Двоичная система счисления

1. Даны 4 целых числа, записанных в двоичной системе:

10001011; 10111000; 10011011; 10110100.

Сколько среди них чисел, больших, чем 9A₁₆?

Пояснение.

Запишем число 9A₁₆ в десятичной системе счисления, а затем переведём его в двоичную: 9A₁₆ = 9 · 16 + 10 = 154₁₀ = 10011010₂. Теперь сравним число 9A₁₆ = 10011010₂ с предложенными числами:

1000 1011 1001 1010,

1001 1011 > 1001 1010,

1011 0100 > 1001 1010.

2. Укажите целое число от 8 до 11, двоичная запись которого содержит ровно две единицы. Если таких чисел несколько, укажите наибольшее из них.

Пояснение.

Представим все числа в двоичной системе счисления:

Из чисел 9 и 10 выбираем число 10, поскольку оно является наибольшим.

3. Даны 4 целых числа, записанных в различных системах счисления: 31₁₀, F1₁₆, 261₈, 711₈. Сколько среди них чисел, двоичная запись которых содержит ровно 5 единиц?

Пояснение.

Представим все числа в двоичной системе счисления.

Среди данных чисел три имеют в записи ровно 5 единиц.

4. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.

Пояснение.

Наименьшее число из пяти единиц в двоичной системе счисления — 1 1111₂. Преобразуем число так, чтобы при переводе в восьмеричную систему счисления получалось четырёхзначное число. Для этого нужно, что число состояло из четырёх триад, то есть состояло из двенадцати символов. Наименьшее число, удовлетворяющее условию задачи: 001 000 001 111₂ = 1017₈.

5. Сколько единиц в двоичной записи восьмеричного числа 1731₈?

Пояснение.

Переведём данное число в двоичную систему счисления: 1731₈ = 001 111 011 001 ₂. 7 единиц.

6. Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 6 нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

Пояснение.

Четырёхзначное, значит, в двоичной записи оно не меньше 1000₁₆ = 1000000000000₂. Чем старше разряд, тем больше он прибавляет к числу. Поэтому нули стоит ставить именно в старшие разряды. Итого получим 1000000111111₂ = 103F₁₆.

7. Сколько единиц в двоичной записи шеснадцатеричного числа 12F0₁₆?

Пояснение.

Переведем число 12F0₁₆ в двоичную систему счисления: 12F0₁₆ = 1001011110000₂.

Подсчитаем количество единиц: их 6.

8. Переведите число В0С₁₆ в двоичную систему счисления.

Пояснение.

9. Сколько единиц в двоичной записи десятичного числа 519?

Пояснение.

Переведём число 519 в двоичную систему:

519₁₀ = 2 9 + 2 2 + 2 1 + 2 0 = 1000000111₂.

10. Переведите в десятичную систему двоичное число 101001₂.

Пояснение.

101001₂ = 1×2 5 + 0×2 4 + 1×2 3 + 0× 2 2 + 0×2 1 + 1×2 0 = 32 + 8 + 1 = 41.

11. Переведите в двоичную систему десятичное число 99.

Пояснение.

Представим число в виде степеней двойки:

12. Даны числа: 1, 3, 11 и 33. Укажите среди них число, двоичная запись которого содержит ровно 3 единицы.

Пояснение.

Переведем числа в двоичную систему счисления:

13. Переведите в шестнадцатеричную систему счисления двоичное число 101011.

Пояснение.

Переведем число в десятичную систему счисления:

101011 = 1 · 2 5 + 1 · 2 3 + 1 · 2 1 + 1 · 2 0 = 32 + 8 + 2 + 1 = 43.

Десятичное число 43 в шестнадцатеричной системе счисления записывается как 2В.

14. Переведите в восьмеричную систему счисления двоичное число 110110.

Пояснение.

Переведем число в десятичную систему счисления:

110110 = 1 · 2 5 + 1 · 2 4 + 1 · 2 2 + 1 · 2 1 = 32 + 16 + 4 + 2 = 54.

Десятичное число 54 в восьмеричной системе счисления записывается как 66.

Источник