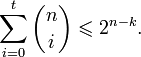кодирование с исправлением ошибок это
Кодирование с исправлением ошибок
Пусть имеется канал связи, содержащий источник помех (см. пример предыдущего параграфа). Помехи проявляются в том, что принятое сообщение может отличаться от переданного. Опишем это отличие в функциональной форме:
называется помехоустойчивым или самокорректирующимся, или кодированием с исправлением ошибок. Можно считать, что А = В = <0,1>. Кроме того, естественно предположить, что содержательное кодирование (вычисление F и выполняется на устройстве, свободном от помех, то есть F и F являются функциями в обычном смысле.
Если про источник помех С ничего не известно, то функции F и F не могут быть определены, за исключением тривиальных случаев, когда 5=0 или |SI = 1. Таким образом, для решения поставленной задачи необходимо иметь описание возможных ошибок (проявлений помех).
Ошибки в канале могут быть следующих типов:
> 0 —>1, 1 —>0 — ошибка типа замещения разряда;
>• е —>1, 8 —? 0 — ошибка типа вставки разряда.
Канал характеризуется верхними оценками количества ошибок каждого типа, которые возможны при передаче через канал сообщения определённой длины п. Общая характеристика ошибок канала (то есть их количество и типы) обозначается S = (Si, S 2, 1 (то есть разряд восстанавливается методом «голосования»). Это кодирование кажется помехоустойчивым для данного канала, однако на самом деле это не так. Дело в том, что хотя можно предполагать, что при передаче сообщения длины 3п возможно не более трех ошибок типа замещения разряда, но места этих ошибок совершенно необязательно распределены равномерно по всему сообщению. Ошибки замещения могут произойти в соседних разрядах, и метод голосования восстановит разряд неверно. Чтобы метод голосования сработал, вместо одного сообщения длины 3п придётся передать три сообщения длины п, то есть уменьшить втрое скорость передачи потока сообщений через канал.
Конспект для учителя по теме «Кодирование с исправлением ошибок»
В статье размещена информация о кодировании с исправлением ошибок, в конце представлено домашнее задание. Материал актуален для подготовки к ЕГЭ.
Введение
Ключевые слова:
В реальных каналах связи всегда присутствуют помехи, искажающие полезный сигнал. В некоторых случаях ошибки допустимы, например при прослушивании радиопередачи через Интернет небольшое искажение звука не мешает понимать речь. Однако чаще всего требуется обеспечить точную передачу данных. Например, ошибка в передаче одной команды компьютерной программы может привести к катастрофе космического корабля. В таких случаях в первую очередь нужно обнаружить ошибку и, если это произошло, передать блок данных ещё раз. Как мы увидим, в некоторых случаях даже удаётся исправить небольшое число ошибок без повторной передачи данных.
Представьте себе, что получена цепочка нулей и единиц 1010101110, причём биты независимы: каждый бит цепочки может быть нулём или единицей независимо от других. В этом случае нет абсолютно никакой возможности определить, верно ли передана последовательность. Поэтому для того, чтобы обнаружить ошибку, в передаваемое сообщение нужно добавлять какую-то дополнительную информацию («лишние» биты), т. е. вводить избыточность.
Простейший вариант — добавить в конец блока данных дополнительный бит, который будет равен 1, если в основном сообщении нечётное число единиц, и равен 0 для сообщения с чётным числом единиц. В результате в новом блоке всегда будет чётное число единиц. Этот дополнительный бит называется битом чётности. Бит чётности используется при передаче данных в компьютерных сетях.
К каждому из этих двухбитных сообщений добавьте бит чётности (так, чтобы общее число единичных битов в каждом сообщении стало чётным):
Сообщения передаются с битом чётности. Какие из этих сообщений были переданы с ошибкой?
00101 0011010101 1001001010011
Как вы думаете, можно ли вместо бита чётности добавлять «бит нечётности», который делает общее число единичных битов в блоке данных нечётным?
К каждому из этих сообщений добавьте бит чётности;
1000 0110 1011101011 11111111
При передаче сообщения с битом чётности произошли две ошибки. Сможет ли обнаружить ошибку принимающая сторона? А если ошибок будет три? Четыре?
Получено сообщение с битом чётности, в котором оказалось нечётное число единиц. Можно ли сказать, в каком именно бите произошла ошибка?
Если при передаче изменились два бита, чётность не меняется, и такая ошибка не обнаруживается. Однако на практике две ошибки в одном небольшом (например, 8-битном) блоке данных могут появиться очень редко.
При передаче больших файлов может сразу возникнуть множество ошибок, поэтому используют другой метод — вычисляют контрольную сумму файла (по достаточно сложным алгоритмам), которая передаётся вместе с данными. Изменение даже одного бита данных сильно изменяет контрольную сумму. Если контрольная сумма файла, вычисленная приёмником, не совпадает с контрольной суммой, записанной передающей стороной, то произошла ошибка.
Коды с исправлением ошибок
Значительно сложнее исправить ошибку сразу (без повторной передачи данных), однако в некоторых случаях и эту задачу удается решить. Для этого ещё больше увеличивают избыточность кода (добавляют «лишние» биты).
Когда вы говорите по телефону, иногда приходится повторять какието фразы, если собеседник не понял вас из-за помех. Эту идею можно использовать и для компьютеров, например применить код, в котором каждый бит повторяется трижды: вместо каждого нуля будем передавать кодовое слово 000, а вместо каждой единицы — кодовое слово 111.
При передаче сообщения каждый передаваемый бит повторяется три раза подряд. Могли ли быть переданы без ошибок такие сообщения?
При передаче каждой тройки одинаковых битов произошло не более одной ошибки. Какие биты пытались передать, если получены тройки битов:
001 010 011 100 101 110?
Передавались сообщения, в которых каждый бит был утроен. При передаче произошли ошибки (не более одной в каждой тройке), и были получены следующие битовые цепочки:
Восстановите битовые цепочки (без утроения), которые передавались.
Код с утроением битов обнаруживает одну или две ошибки. Кроме того, если сделана одна ошибка, он позволяет исправить её, т. е. является помехоустойчивым.

Попробуйте придумать другой трёхбитовый код (содержащий два кодовых слова), который позволяет исправлять одну ошибку и обнаруживать одну или две ошибки. Что общего в коде с утроением битов и в вашем коде?
Кроме простого дублирования битов есть и другие, более сложные помехоустойчивые коды. Например, предположим, что передаются сообщения, содержащие только четыре буквы — «П», «О», «Р», «Т». Для кодирования букв используются 5-битные кодовые слова (рис. 2.9).
Рис. 2.9
Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора различаются не менее чем в трёх битах. В этом случае говорят, что расстояние Хэмминга между кодовыми словами больше или равно трём. Например, слова «П» — 111.11 и «О» — 11000 различаются в трёх последних битах, а слова «П» — 11111 и «Р» — 00100 — в четырёх битах (они подчёркнуты). Это позволяет обнаруживать и даже исправлять ошибки.
Для передачи данных использовался код, заданный на рис. 2.9. Принята цепочка 00110. Определите букву, код которой отличается от этой цепочки меньше всего.
Для передачи данных использовался код, заданный на рис. 2.9. Принята цепочка 10101. Определите знаки, коды которых отличаются от этой цепочки меньше всего.
Для передачи данных использовался код, заданный на рис. 2.9. При передаче каждого кодового слова произошло не более двух ошибок. Декодируйте сообщение, исправив ошибки: 00111 11100 11110 11000 00000 01110 11011 11100 00011 11000
Если ошибку исправить нельзя, поставьте символ «
В каком случае при использовании кода, заданного на рис. 2.9:
а) можно обнаружить ошибки, а исправить нельзя;
б) нельзя даже обнаружить ошибки?
Если все кодовые слова отличаются друг от друга не менее чем в трёх битах, такой код позволяет обнаружить одну или две ошибки. Если сделана только одна ошибка, код позволяет исправить её. Если же произошли три ошибки и более, в результате мог получиться другой правильный код, и эти ошибки обнаружить нельзя.
Выводы
Интеллект-карта
Рис. 2.10
Домашнее задание
1. Почему код с обнаружением и/или исправлением ошибок должен быть избыточным?
2. Сравните коды, использующие бит чётности и коды, использующие контрольную сумму. Какие достоинства и недостатки имеет каждый метод?
3. Зачем нужны коды, которые позволяют обнаружить ошибки, но не позволяют их исправить?
4. Сравните код, в котором каждый бит повторяется три раза, и код на рис. 2.9. Какой из них более экономичный, т. е. требует меньше «лишних» битов?
5. Как вы думаете, почему бы не использовать везде только помехоустойчивые коды?
Коды, исправляющие ошибки
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Содержание
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 
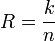
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 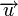

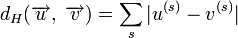
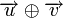
Минимальное расстояние Хемминга 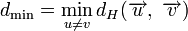
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром

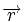
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 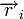

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 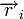
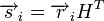
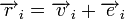
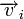
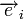

Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 
Порождающий (генераторный) полином
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
Коды CRC
Таким образом, вид полинома g(x) задаёт конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | x 12 + x 11 + x 3 + x 2 + x + 1 |
| CRC-16 | 16 | x 16 + x 15 + x 2 + 1 |
| CRC-x 16 + x 12 + x 5 + 1 | ||
| CRC-32 | 32 | x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1 |
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома g(x) на множители в поле Галуа.
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
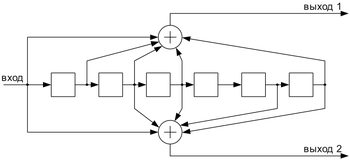
Свёрточные коды
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
Литература
Ссылки
Смотреть что такое «Коды, исправляющие ошибки» в других словарях:
Коды исправляющие ошибки — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Исправляющие ошибки Коды — Обнаружение ошибок в технике связи действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) процедура восстановления информации после… … Википедия
Коды Рида-Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код Рида Соломона является … Википедия
КОРРЕКТИРУЮЩИЕ КОДЫ — коды, обнаруживающие и исправляющие ошибки при передаче и обработке информации в линиях связи или сложных информац. системах. В основе корректирования лежит использование избыточности сообщений, при к рой часть символов кодового слова можно… … Большой энциклопедический политехнический словарь
Корректирующие коды — помехоустойчивые коды, коды обнаружения и исправления ошибки, Коды, позволяющие по имеющейся в кодовой комбинации избыточности (См. Избыточность) обнаруживать и исправлять определённые ошибки, появление которых приводит к образованию… … Большая советская энциклопедия
Код Рида — Коды Рида Соломона (англ. Reed–Solomon codes) недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона,… … Википедия
Код коррекции ошибок Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
Код Рида-Соломона — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
РС код — Коды Рида Соломона недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида Соломона, работающие с байтами (октетами). Код… … Википедия
Код Боуза — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия