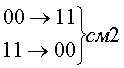кодирование с проверкой на четность

Кодирование с проверкой на четность

Широкое распространение в вычислительной технике получил метод кодирования с проверкой на четность. Для этого метода выполняют суммирование цифр по модулю 2, входящих в контролируемый код. Вместе с передаваемым кодом передается один контрольный разряд. Его значение («1» или «О») выбирается с условием, чтобы сумма цифр в передаваемом коде была по модулю 2 равна 0 — для случая четности или 1 — для случая нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка. Пример реализации метода кодирования с проверкой на четность представлен в табл. 2.3.

Пример реализации метода кодирования с проверкой на четность

Можно представить несколько измененный метод кодирования с проверкой на четность. Длинное число разбивается на группы, каждая из которых содержит / разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно схеме (рис. 2.3).

Рис. 2.3. Схема исходной комбинации

Увеличение избыточности передаваемых кодов приводит к тому, что появляется возможность не только обнаружить, но и исправить ошибку. Если произошла ошибка в одном из разрядов, то при проверке на четность сумма по соответствующим строкам и столбцам изменится. Зафиксируется нарушение четности в строке и столбце, что будет означать обнаружение не только ошибки, но и ее места. При изменении содержимого отмеченного разряда на противоположное ошибка исправляется.

Описанный метод широко используется для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях, а также при выполнении арифметических операций.

Признаком отсутствия искажений в процессе приема-передачи является равенство контрольного числа нулю.

Источник

28. Кодирование по методу четности-нечетности.

koralexand.ru > 28. Кодирование по методу четности-нечетности.

Кодирование по методу четности-нечетности

Кодирование с контролем четности (нечетности) является простейшим видом помехоустойчивого кодирования. Метод состоит в следующем.

В математическом коде выделяется один контрольный разряд (k). К каждому двоичному числу добавляется один избыточный раз­ряд и в него записывается 1 или 0 с таким условием, чтобы сумма цифр в каждом числе была по модулю 2 равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнаружится по на­рушению четности (нечетности). При таком кодировании допускается, что может возникнуть только одна ошибка. Пример реали­зации метода четности представлен в таблице 15.

1010101110110010100010010001101100101101 — нарушение

Такое кодирование имеет минимальное кодовое расстояние, равное 2.

Можно представить и несколько видоизмененный способ контроля по методу четности — нечетности, используя так называемые матричные проверки и суммирование производить не только по строкам, но и по столбцам. Длинное число разбивается на группы, ка­ждая из которых содержит l разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно следующей схеме:

kj

sj

Пример. Определить и исправить ошибку в передаваемой информации вида

1	0	0	1	1	1	0	0	0
1	1	1	0	1	0	1	0	1
0	1	0	1	1	0	1	0	0
1	0	1	0	1	1	0	0	0
1	1	0	1	0	1	1	1	0
0	0	0	1	0	1	1	kj
0	1	0	0	0	0	0	sj

Для контроля использован, метод четности по строкам и столбцам (контрольный стол­бец 8, контрольная строка 6).

Решение: Осуществим проверку на четность по каждой строке: s₁=0; s₂=1; s₃=0; s₄=0; s₅=0.

Затем проверим на четность информацию по столбцам:

Проверка показывает, что ошибка возникла в разряде второй строки и второго слева столбца. Следовательно, разряд, содержащий ошибочную информацию, находится на пере­сечении второй строки и второго столбца.

1	0	0	1	1	1	0	0
1	0	1	0	1	0	1	0
0	1	0	1	1	0	1	0
1	0	1	0	1	1	0	0
1	1	0	1	0	1	1	1
0	0	0	1	0	1	1	kj

Контроль по методу четности-нечетности широко используют в ЭВМ для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях, а также при выполнении арифметических операций.

Оставить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Источник

Помехоустойчивое кодирование с иcпользованием различных кодов

Это продолженеие статьи о помехоустойчивом кодировании, которая очень долго лежала в черновиках. В прошлой части нет ничего интересного с практической точки зрения — лишь общие сведения о том, зачем это нужно, где применяется и т.п. В данной части будут рассматриваться некоторые (самые простые) коды для обнаружения и/или исправления ошибок. Итак, поехали.

Попытался все описать как можно легче для человека, который никогда не занимался кодированием информации, и без каких-либо особых математических формул.

Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.

По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Избыточность кода — это количество проверочной информации в сообщении. Рассчитывается она по формуле:

k/(i+k), где
k — количество проверочных бит,
i — количество информационных бит.

Например, мы передаем 3 бита и к ним добавляем 1 проверочный бит — избыточность составит 1/(3+1) = 1/4 (25%).

Код с проверкой на четность

Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.

Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.

Код Хэмминга

первый проверочный бит на 2 0 = 1;
второй проверочный бит на 2 1 = 2;
третий проверочный бит на 2 2 = 4;

r1 = i1 + i2 + i4
r2 = i1 + i3 + i4
r3 = i2 + i3 + i4

В принципе, работа этого алгоритма разобрана очень детально в статье Код Хэмминга. Пример работы алгоритма, так что особо подробно описывать в этой статье не вижу смысла. Вместо этого приведу структурную схему кодера:

и декодера

(может быть, довольно запутано, но лучше начертить не получилось)

e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:

e0 = k1 + k3 + k5 + k7 mod 2
e1 = k2 + k3 + k6 + k7 mod 2
e2 = k4 + k5 + k6 + k7 mod 2

Набор этих значений e2e1e0 есть двоичная запись позиции, где произошла ошибка при передаче данных. Декодер эти значения вычисляет, и если они все не равны 0 (то есть не получится 000), то исправляет ошибку.

Коды-произведения

В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке:

Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке:

Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования. Здесь к ним добавляются проверочные символы, а они, в свою очередь, заносятся в буфер по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.

При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается куда-нибудь. Условимся, что и внутренний, и внешний коды – коды Хэмминга, с тремя проверочными символами, то есть и тот, и другой могут исправить по одной ошибке в кодовом слове (количество «кубиков» на рисунке не критично — это просто схема). На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (крестики на рисунке в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена.

Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце — две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.

Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.

Источник

Код с проверкой на четность

Коды с обнаружением ошибок

Методы помехозащищенного кодирования направленные только на обнаружение ошибки называют – коды обнаружения ошибок. Обнаружение ошибки позволяет, в некоторых ситуациях, перезапросить данные с источника и исправить ошибку. Ну или не использовать ошибочные данные. Поскольку коррекция ошибок в этих методах не требуется, то размер дополнительно передаваемой информации минимален.

Простейшим кодом обнаружения ошибок является «контроль четности».

Код с проверкой на четность

Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных.

Всё сообщение разбивается на блоки бит равного размера, например, по 8-мь бит. И вычисляется сумма значений бит каждого из этих блоков. К блоку добавляется еще один бит: если сумма нечетная, то бит 1, иначе — бит 0. Т.е. получается блок длиной на один бит больше исходного — это «бит четности», так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.

При получении данных вычисление «бита четности» повторяется и результат сравнивается с переданным битом четности. Если вычисленное и переданное значение «бита четности» совпадают, значит ошибки не было, иначе — ошибка.

С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку. Такой код образуется путем добавления к передаваемой комбинации, состоящей из k информационных символов, одного контрольного символа (0 или 1), так, чтобы общее число единиц в передаваемой комбинации было четным.

Легко сообразить, что искажение двух, четырех и любого четного количества бит в блоке не будет обнаружено.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.

Как говорилось ранее, этот метод служит только для определения одиночной ошибки. В случае изменения состояния двух битов, возможна ситуация, когда вычисление контрольного бита совпадет с записанным. В этом случае система не определит ошибку, а это не есть хорошо.

Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.

Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.

Решите задачу 1:

Закодируйте слово длины 4 с помощью кода с проверкой четности.

а) α=(0011)	б) α=(1011)	в) α=(0111)	г) α=(0001)	д) α=(0010)
е) α=(1010)	ж) α=(0110)	з) α=(1001)	и) α=(1000)	к) α=(1100)

Образец: Закодируйте слово α=(0101) длины 4 с помощью кода с проверкой четности.

Решение: Найдем сумму по модулю 2 всех двоичных букв этого слова. Имеем:

, поэтому передано будет сообщение в виде слова b=(01010) длины 5.

Решите задачу 2:

Декодируйте слово длины 5 с помощью кода с проверкой четности

а) b=(00110)	б) b=(10111)	в) b=(01110)	г) b=(00011)	д) b=(00101)
е) b=(10100)	ж) b=(01100)	з) b=(10010)	и) b=(10001)	к) b=(11001)

Образец: Декодируйте слово b=(01110) длины 5 с помощью кода с проверкой четности.

Решение: Отбросив последнюю букву передаваемого слова, имеем слово α=(0101) длины 4, которое передавалось по каналу связи.

Решите задачу 3:

Определите, допущены ли ошибки в сообщении, заданном в задании 2.

Образец: Определите, допущены ли ошибки в сообщениях a₁=(01110) и a₂= (01010).

Решение: Для обнаружения ошибки, проверим с помощью М2 сумму всех букв закодированного слова в полученных сообщениях: a₁= . Т.к. сумма всех букв закодированного слова оказалась равной 1, то при его передаче по каналу связи была допущена ошибка.

Для второго сообщения имеем a₁= 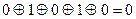. Т.к. сумма всех букв закодированного слова оказалась равной 0, то при его передаче по каналу связи код с проверкой четности не позволяет выявить ошибку.

1.2 Код «циклическая сумма»

Другим примером кодов обнаружения ошибок является «циклическая сумма» (Cyclic Redundancy Checksum или CRC). Этот метод является неблочным, но может быть использован и в блочном варианте. Принцип обнаружения ошибки схож с кодом «контроля четности». Используя особый алгоритм суммируются значения всех битов данных или порции данных, в результате суммирования получается некое число (не один бит, а несколько), которое передается вместе с данными или порцией данных. Принимающая сторона вычисляет CRC повторно и сравнивает с переданным.

«Контроль четности» — частный случай CRC.

1.2. Код с постоянным весом (блочный неразделимый)

В теории кодирования весом кодовых комбинаций принято называть количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код позволяет обнаруживать любые одиночные ошибки и часть многократных ошибок. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации, когда одновременно одна единица переходит в ноль и один ноль переходит в единицу, два ноля и две единицы меняются на обратные символы и т.д. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей.

Примером кода с постоянным весом является Международный телеграфный код МТК-3. В этом коде все разрешенные кодовые комбинации имеют вес равный трем, разрядность же комбинаций n=7. Таким образом, из 128 комбинаций (N₀ = 2 7 = 128) разрешенными являются Nа = 35 (именно столько комбинаций из всех имеют W=3). При декодировании кодовых комбинаций осуществляется вычисление веса кодовой комбинации и если W<>3, то выносится решение об ошибке. Например, из принятых комбинаций 0110010, 1010010, 1000111 ошибочной является третья, т. к. W=4.

Рассмотрим код с тремя единицами из семи. Для этого кода возможны смещения трех типов.

Например, код при коэффициент обнаружения составит , избыточность L=27%.

Пример. Коды с двумя единицами из пяти и тремя единицами из семи.

Код Грея

Для уменьшения вероятности ошибки в двоичных кодах используют код Грея, в котором каждые две позиции отличаются только одним разрядом, т.е. на 1 бит. Поэтому выходной сигнал может быть представлен лишь одним из двух состояний: истинный или ложный. Код Грея тоже использует лишь два знака 0 и 1, но соседние числа отличаются только в одном разряде, т.е. на 1 бит информации.

Источник

Кодирование с проверкой на четность

Широкое распространение в вычислительной технике получил метод контроля кодов по признаку четности-нечетности. Для этого метода выполняют суммирование цифр по модулю два, входящих в контролируемый код. Вместе с передаваемым кодом передается один контрольный разряд. Его значение (1 или 0) выбирается с условием, чтобы сумма цифр в передаваемом коде была по модулю два равна 0 для случая четности и 1 – для случая нечетности. При таком кодировании допускается, что может возникнуть только одна ошибка. Пример реализации метода четности представлен в таблице 2.3.

Исходная комбинация	Контрольный разряд	Проверка
1 – ошибка

Можно представить несколько измененный способ контроля по методу четности-нечетности. Длинное число разбивается на группы, каждая из которых содержит разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно схеме:

Увеличение избыточности передаваемых кодов приводит к тому, что появляется возможность не только обнаружить, но и исправить ошибку. Пусть произошла ошибка в одном из разрядов. Это приведет к тому, что при проверке на четность сумма по соответствующим строкам и столбцам изменится. Зафиксируется нарушение четности в строке и столбце, что означает обнаружение не только ошибки, но и ее места. Изменив содержимое отмеченного разряда на противоположное, исправляется ошибка.

Контроль по методу четности-нечетности широко используется для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях, а также при выполнении арифметических операций.

Признаком отсутствия искажений в процессе приема-передачи является значение контрольного числа по методу проверки на четность равное нулю.

Кодирование с удвоением элементов

Данный метод кодирования характеризуется дополнительными символами для каждого информационного символа передаваемого кода. Информационная «1» представляется 10, а «0» 01. Например, исходная комбинация 1011 преобразуется в 10011010. Показателем искажения являются сочетания типа 00 и 11 в «парных» элементах. Код не исправляет ошибки, приводящие к двукратным противоположным изменениямразрядов в парных элементах. Помехоустойчивость данного кода выше, чем кода с проверкой четности-нечетности, но при этом существенно возрастает избыточность кода.

Инверсное кодирование

В основе метода лежит повторение кодовой комбинации. Если исходная комбинация содержит четное число единиц, вторая, повторная комбинация в точности повторяет исходную. Иначе повторение происходит в инверсном виде. Например, комбинация 01010 в инверсном коде представляется как 0101001010; 11010 1101000101. Проверка производится суммированием единиц основной комбинации. Если их число четно, то элементы второй части принимаются в том же виде. После чего обе части комбинации сравниваются поэлементно, т.е. первый элемент первой части с первым элементом второй части. При несовпадении хотя бы одного элемента принятая комбинация считается неверной.

Инверсный код позволяет обнаружить практически все ошибки приема-передачи. Не обнаруживаются лишь ошибки, где произошло одновременное искажение парных элементов в обеих частях комбинации.

Код Хемминга

Рассмотрим код Хемминга, исправляющий одиночные ошибки.

Необходимое количество проверочных символов r или значность кода для кодов Хемминга, исправляющих одиночные ошибки определяется из ранее полученного соотношения:

Значения проверочных символов и номера их позиций по методу Хемминга устанавливается одновременно с выбором контролируемых групп кодовых комбинаций. При этом исходят из следующего: в результате первой проверки получают контрольное число, если оно равно 1, то один из символов первой проверенной группы искажен. Для выяснения вопроса, какой из символов может быть искажен, рассмотрим таблицу 2.4, в которой представлен натуральный ряд четырехразрядных контрольных чисел в двоичной системе счисления.

№ п./п.	Символы разрядов контрольного числа
(ст)	(мл)

Как видно из таблицы 2.4, если младший разряд контрольного числа содержит 1, то искажение должно быть в одной из нечетных позиций кодовой комбинации. Следовательно, первой проверкой должны быть охвачены символы с нечетными номерами. Если результат второй проверки даст 1, то получим 1 во втором разряде контрольного числа. Следовательно, второй проверкой должны быть охвачены символы с номерами, содержащими 1 во втором разряде двоичной записи этого номера: 2, 3, 6, 7, 10 и т.д. Аналогично при третьей проверке проверяться символы, номера которых в двоичной записи содержат 1 в третьем разряде: 4, 5, 6, 7, 12 и т.д.

Такие рассуждения позволяют образовать таблицу 2.5 проведения проверок.

№ проверки	номера проверяемых позиций	номера позиций контрольных символов
1,3,5,7,9,11,13. 2,3,6,7,10. 4,5,6,7,12. 8,9,10,11,12.

Если символы проверяемой кодовой комбинации обозначить через a_i, то проверочные суммы S_i можно записать следующим образом:

Номер позиции символа, в котором произошла ошибка в процессе приема-передачи комбинации, определяется следующим двоичным числом: N₂=. S_i. S₄ S₃ S₂ S₁.

При передаче значения проверочных символов устанавливаются в кодовой комбинации такими, чтобы суммы S равнялись нулю (т.е. были бы четными числами), т.е. значения проверочных символов а₁, а₂, а₄. выбираются из условия равенства S_i нулю.

Представим в качестве примера в коде Хемминга двоичную комбинацию 10010. Для нее число информационных символов m=5, при этом максимальное число передаваемых кодов равно 32. Разрядность кода Хемминга для m=5 должна быть равной 9 (n=9). Для девятиразрядного кода символы а₁, а₂, а₄ и а₈ являются проверочными, а символы а₃, а₅, а₆, а₇ и а₉ — информационными. Для заданного кода а₃=0, а₅=1, а₆=0, а₇=0 и а₉=1, тогда:

Следовательно, код Хемминга для кода 10010 будет равен 110011000.

Если произойдет однократная ошибка приема-передачи первого символа кодовой комбинации, то сумма S₁ будет равна 1, а остальные суммы будут равны 0. Полученное контрольное число N будет равно 0001, что указывает на искажение первого символа принятого кода. Аналогичные контрольные числа будут получены при искажениях 2-го, 3-го и т.д. символов кода. Отметим, что для исправления ошибки принятой кодовой комбинации необходимо лишь изменить значение искаженного символа на противоположное.

Источник