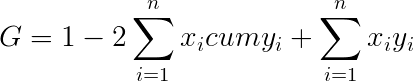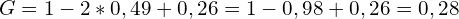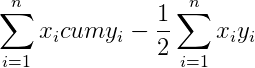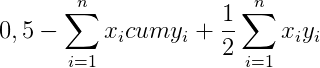коэффициент джини машинное обучение
Gini & ROC & Precision-Recall: проблемы метрик в банковском моделировании
Метрики Gini и AUC-ROC применяются в банковском скоринге уже много лет в качестве основных метрик для сравнения качества моделей. Начальник управления расследования мошенничества КБ «Ренессанс Кредит» Сергей Афанасьев и руководитель направления моделирования и оперативного анализа КБ «Ренессанс Кредит» Анастасия Смирнова показывают недостатки данных метрик и предлагают альтернативные бизнес-метрики, которые определяются через бизнес-цели банка и выражаются в денежном эквиваленте.
Бинарные классификаторы являются, пожалуй, наиболее популярными методами машинного обучения, применяемыми на практике.
В банковской сфере модели бинарной классификации используются практически во всех ключевых направлениях деятельности:
— в скоринге это модели прогнозирования вероятности дефолта заемщика;
— в перекрестных продажах (CRM) — модели отклика клиента на x-sell предложение;
— во взыскании — модели прогнозирования вероятности возврата просроченного кредита;
— в антифроде — модели выявления мошеннических кредитов;
— и т.д.
Бинарная классификация используется в задачах, где объекты выборки делятся на два класса — положительные (positive) и отрицательные (negative) (рис. 1а). Применительно к банковским задачам это могут быть следующие разбиения:
— попадет кредит в просрочку (1 — positive) или нет (0 — negative);
— откликнется клиент на x-sell предложение банка (1) или нет (0);
— вернет клиент просроченный кредит (1) или не вернет (0);
— окажется кредитная заявка мошеннической (1) или нет (0);
— и т.д.
В свою очередь сама модель бинарной классификации присваивает объектам также две метки — positive или negative (см. рис. 1а). А поскольку моделям свойственно ошибаться, то в результате бинарной классификации все объекты выборки разбиваются на четыре типа, образуя матрицу ошибок (confusion matrix) (рис. 1б):
1) истинно положительные (true positive — TP);
2) истинно отрицательные (true negative — TN);
3) ложно положительные (false positive — FP) — ошибка 1-го рода (type I error);
4) ложно отрицательные (false negative — FN) — ошибка 2-го рода (type II error).
Рисунок 1
Метрики качества бинарных классификаторов делятся на «пороговые» (single-threshold) и «не зависящие от порога» (threshold-free).
Бинарные классификаторы обычно настраиваются на прогноз вероятности принадлежности к одному из двух классов. То есть каждому объекту присваивается числовое значение в диапазоне от 0 до 1 (или от 0 до 999 для скорингового балла). Таким образом, чтобы разделить прогнозные значения на два класса, необходимо выбрать порог, разбивающий весь диапазон значений на две группы. После выбора порога можно построить матрицу ошибок, на основе которой рассчитываются различные «пороговые» метрики качества. Формулы для популярных пороговых метрик качества представлены в табл. 1.
Если переменные в матрице ошибок рассчитать для различных порогов, то можно построить метрики качества, не зависящие от порога, такие как Gini, AUC-ROC и др. (табл. 2).
Рисунок 2
Рисунок 3
Результаты наших экспериментов подтверждают перечисленные недостатки Gini и AUC-ROC для несбалансированных выборок (табл. 3, 4).

где P (Profit) — прибыль портфеля;
G (Good) — портфель «хороших» кредитов;
B (Bad) — портфель «плохих» кредитов;
m (margin) — маржа по «хорошим» кредитам с учетом OPEX-расходов;
RR (recovery rate) — коэффициент восстановления «плохих» кредитов (какая часть просроченных кредитов взыскана с должников).
В обозначениях матрицы ошибок формула (1) переписывается в виде:
P=m×TN×s-(1-RR)×FN×s, (2)
где TN — количество истинно отрицательных объектов («хорошие» кредиты);
FN — количество ложно отрицательных объектов («плохие» кредиты);
s — средний чек по выданным кредитам.
Аналогичную метрику можно использовать для моделей детектирования заявочного мошенничества.
Для моделей выявления внутреннего мошенничества лучше использовать другую бизнес-метрику — потенциальный убыток. Данная метрика позволяет настраивать правила на раннее обнаружение мошенничества, а не на констатацию уже свершившегося убытка.
В задачах CRM для оценки моделей отклика клиентов необходимо максимизировать прибыль от выданных кредитов за вычетом расходов на звонки или SMS:
P=m×TP×s-c×(TP+FP), (3)
где TP — количество истинно положительных объектов (откликнувшиеся клиенты);
FP — количество ложно положительных объектов (не откликнувшиеся клиенты);
m — маржа на выданный кредит;
s — средний чек по выданным кредитам;
c — затраты на звонки (или SMS) в пересчете на одну одобренную заявку (включая невыданные кредиты).
Коэффициент Джини. Из экономики в машинное обучение
Комментарии 17
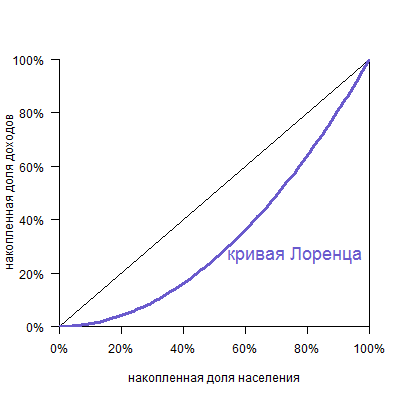
Прочитав статью понял, что как и те комментаторы, которые отвечали, что формула (2) для них очевидна, я находился в заблуждении о том, что кривая Лоренца, в известном смысле эквивалентна ROC кривой. А вот Lift кривая эквивалентна кривой CAP en.wikipedia.org/wiki/Cumulative_accuracy_profile
(хотя с многозначностью термина Lift, тоже все плохо). Вы убедительно показали, что, как раз, кривая Лоенца, эквивалентна кривой CAP, а не ROC.
Проблема в том, что в той сфере, в которой индекс Джини активно используется на практике (сравнительный анализ моделей банковского скоринга) под индексом Джини (те кто об этом задумываются) понимают именно нормализованный индекс Джини. И, действительно, вычисляют его на основании ROC AUC по формуле (2), а не на основании CAP AUC.
Вопрос для меня не праздный, сталкиваюсь с ним ежедневно. Мы даже, нашу компанию, назвали GiniMachine.
Статья, конечно, помогла развеять мифы, как Вы и надеялись, но, боюсь, как в известной миниатюре xkcd про стандарты, ситуацию это, скорее, усугубило. ( xkcd.ru/927 )
С другой стороны, 30 лет назад невозможно было представить, что заблуждение по поводу именования мото-любителей и меломанов когда-нибудь удастся преодолеть…
P.S. обстоятельная статья 15 летней давности, на тему ROC и CAP, от Бундесбанка. Раньше я не понимал почему авторы избегают упоминания индекса Джини, теперь мне кажется, это не случайность. www.bundesbank.de/Redaktion/EN/Downloads/Publications/Discussion_Paper_2/2003/2003_10_01_dkp_01.pdf?__blob=publicationFile
На практике, с тем, чтобы наши клиенты для «не нормализованного» индекса Джини использовали отдельный термин Accuracy Rate — сталкиваться не доводилось. Хотя, в литературе, с этим термином в таком смысле я сталкивался, но не придавал значения разнице в определении. Вот тут например: journal.fsv.cuni.cz/storage/1228_rezac.pdf
Любопытно, что в этой статье даже явно пишут о том, что Lorenz Curve путают с Receiver Operating Characteristic. Но, при этом, если я не запутался в их нотации, определяют её именно как зеркальную (по диагонали) ROC кривую, противопоставляя ей CAP кривую, которую называют также Lift кривой.
Вот с чем не редко приходится сталкиваться на практике, так это с тем, что представители бизнеса (не специалисты-рисковики) могут интерпретировать индекс Gini именно как accuracy модели для задачи бинарной классификации. Т.е. индекс Джини в 0.8 интерпретируют как 20 ошибок первого или второго рода из 100 случаев.
Когда приводишь «контр-пример», мол, если всего 10 процентов займов не погашаются вовремя, то даже если мы будем одобрять всем, то достигнем accuracy в 90%, тогда начинается содержательный разговор. И, нужно отметить, что представители бизнеса, на моей памяти, всегда очень радовались, уделив время и разобравшись. Вот прям, не побоюсь этого слова, именно — радовались.
Анализ малых данных
КвазиНаучный блог Александра Дьяконова
Знакомьтесь, Джини
Многие путаются в коэффициентах Джини, не понимают, что они бывают разные и для разных задач (и названия у них разные — просто в русском переводе, как всегда, многое схлопывается в один термин).
Есть коэффициент/индекс Джини (Gini coefficient), который используют при оценке качества классификации и регрессии. На русской странице Wiki не очень информативно, но вот на английской всё подробно: изначально это был статистический показатель степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку. Вычисляется как отношение площади фигуры, образованной кривой Лоренца и кривой равенства, к площади треугольника, образованного кривыми равенства и неравенства. Сейчас поясню.
Допустим, в компании работают 4 человека с суммарным доходом 8000$. Равномерное распределение дохода — это 2000$+2000$+2000$+2000$, неравномерное — 0$+0$+0$+8000$. А как оценить неравномерность, скажем, для случая 1000$+1000$+2000$+4000$? Упорядочим сотрудников по возрастанию дохода. Построим кривую (Лоренца) в координатах [процент населения, процент дохода этого населения] — идём по всем сотрудникам и откладывает точки. Для первого — [25%, 12.5%] — это сколько он составляет процентов от всего штата и сколько процентов составляет его доход, для первого и второго — [50%, 25%] — это сколько они составляют процентов и сколько процентов их доход, для первых трёх — [75%, 50%], для всех — [100%, 100%].

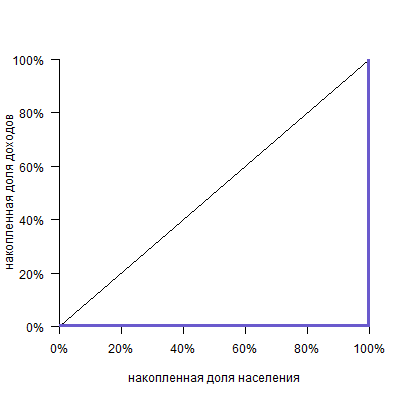
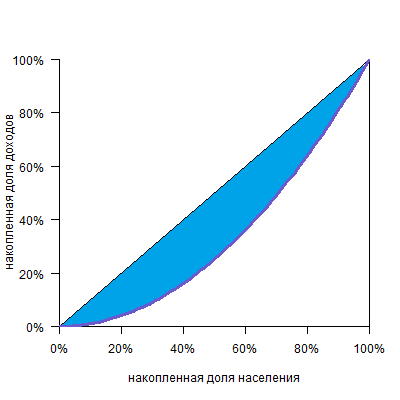
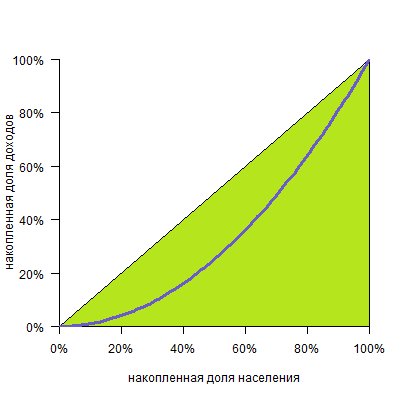
На. Рис. 1. построенная кривая Лоренца показана красным цветом. Кривая Лоренца, которая соответствует равномерному распределению дохода, — синяя диагональ (т.н. кривая равенства). Кривая Лоренца, которая соответствует неравномерному распределению, — зелёная (т.н. кривая неравенства). Вот площадь A, делённая на A+B=0.5, и есть коэффициент Gini.
При оценке качества классификации GINI = 2*AUCROC-1. Про AUCROC я уже как-то писал. Почему это они так связаны нигде подробно не описано. Я нашёл упоминание в работе Supervised Classification and AUC. Там всё логично: если в задаче классификации на два класса 0 и 1 интерпретировать эти числа как доходы. Но чтобы связь была именно GINI = 2*AUCROC-1, должно быть что-то типа рис. 2 (но ROC-кривая и кривая Лоренца это не одно и то же), кстати в презентации Credit Scoring and the Optimization concerning Area under the curve такая же картинка.

Есть ещё коэффициент/индекс Джини (Gini impurity), который используется в решающих деревьях при выборе расщепления. Я дал ссылку на английскую Wiki, поскольку русского аналога нет. Он тоже измеряет «равномерность», если p_i — частоты представителей разных классов в листе дерева, то коэффициент Джини для него равен
Только вот это другая равномерность, никак не связанная с рассмотренной ранее. Для первой нужно два показателя — доход и численность населения с таким доходом, а тут только проценты (частоты). В английской версии на странице Gini coefficient написано «не путать с Gini impurity» и наоборот.
Я не знаю, как лучше переводить impurity, скажем, С.П.Чистяков переводит как «загрязненность» (на мой взгляд, не очень звучит…).
Коррадо Джини (Corrado Gini, 1884), который всё это придумал был итальянским статистиком. Но кроме этого, он известный идеолог фашизмa, написал книгу «Научные основы фашизма». Прожил, кстати, довольно много — 80 лет, видимо, после войны не преследовался. Вот так бывает…
Как рассчитывать коэффициент Джини
Автор: Игорь Святославович Демин · Опубликовано 21.11.2017 · Обновлено 19.01.2021
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
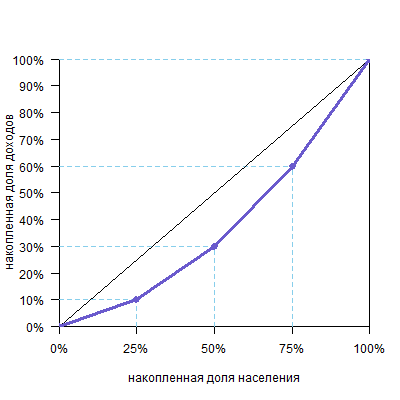
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
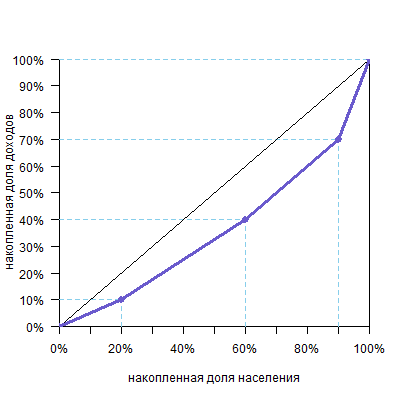
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
Получим такой график:
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
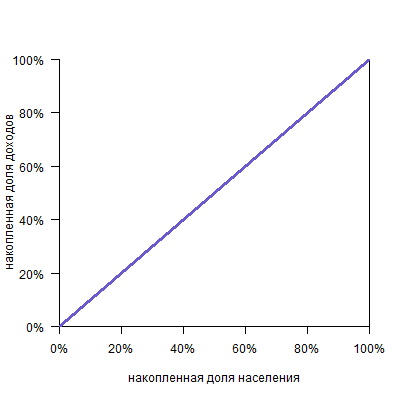
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
К площади треугольника под диагональю (а она всегда равна 0,5):
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
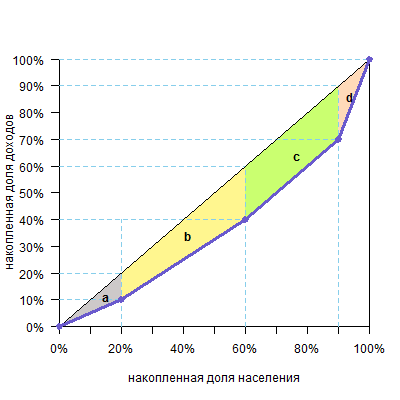
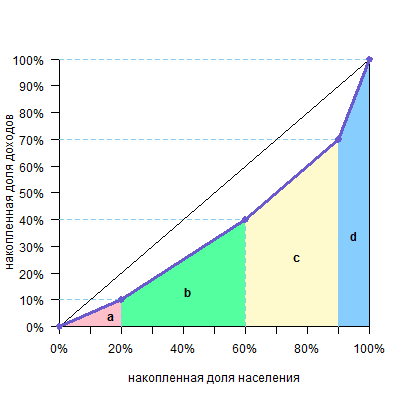
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
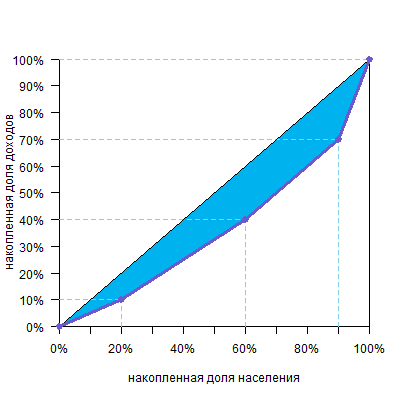
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:
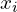
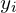
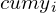
Составим таблицу на основе данных предыдущего примера:
| Доля населения ( 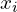 ) ) | Доля от общего дохода ( 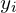 ) ) | Накопленная доля общего дохода ( 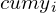 ) ) | 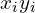 | 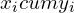 |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Как построена эта таблица
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
Как выведена эта формула?
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
можно сперва посчитать площадь фигуры под кривой Лоренца
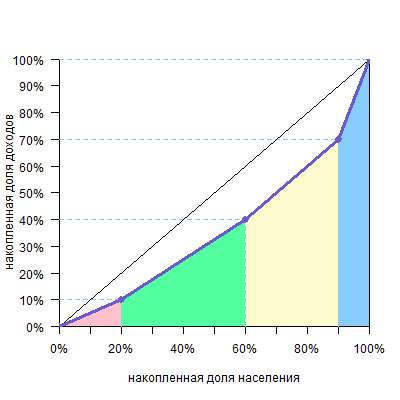
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
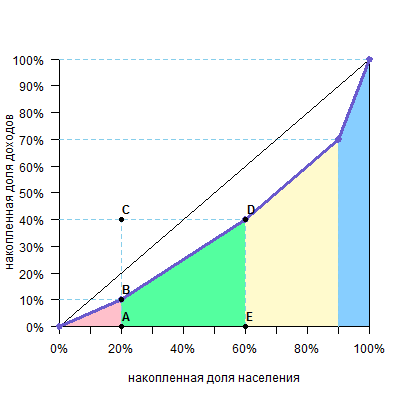
Рассмотрим, например, вторую группу (зеленый четырехугольник).
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.\