композиции алгоритмов машинного обучения

Методы сбора ансамблей алгоритмов машинного обучения: стекинг, бэггинг, бустинг

Что такое ансамбли моделей?

Стекинг. Могут рассматриваться разнородные отдельно взятые модели. Существует мета-модель, которой на вход подаются базовые модели, а выходом является итоговый прогноз.

Бэггинг. Рассматриваются однородные модели, которые обучаются независимо и параллельно, а затем их результаты просто усредняются. Ярким представителем данного метода является случайный лес.

Бустинг. Рассматриваются однородные модели, которые обучаются последовательно, причем последующая модель должна исправлять ошибки предыдущей. Конечно, в качестве примера здесь сразу приходит на ум градиентный бустинг.

Рисунок 1

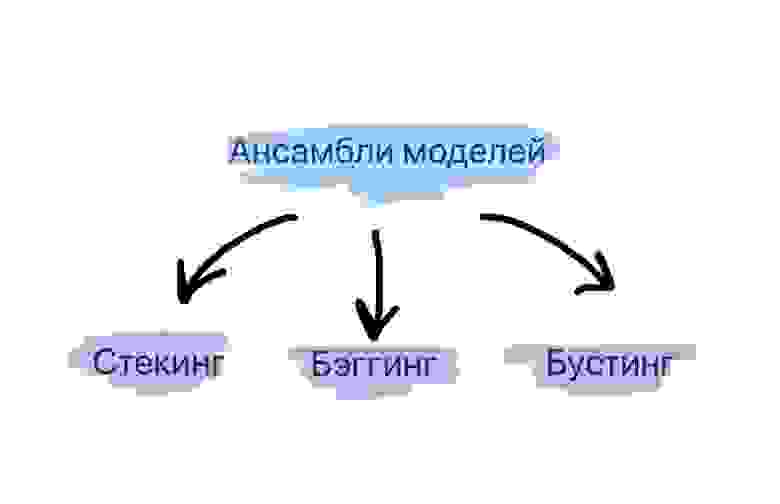
Три этих способа и будут детальнее рассмотрены далее.

Стекинг

Из трех вариантов стекинг является наименее популярным. Это можно проследить и по числу готовых реализаций данного метода в программных библиотеках. В том же sklearn.ensemble в python куда чаше используют AdaBoost, Bagging, GradientBoosting, чем тот же самый Stacking (хотя его реализация там тоже есть).

Стекинг выделяется двумя основными чертами: он может объединить в себе алгоритмы разной природы в качестве базовых. Например, взять метод опорных векторов (SVM), k-ближайших соседей (KNN) в качестве базовых и на основе их результатов обучить логистическую регрессию для классификации. Также стоит отметить непредсказуемость работы метамодели. Если в случае бэггинга и бустинга существует достаточно четкий и конкретный ансамблевый алгоритм (увидим далее), то здесь метамодель может с течением времени по-разному обучаться на входных данных.

Алгоритм обучения выглядит следующим образом (рис. 2):

Делим выборку на k фолдов (тот же смысл, что и в кросс-валидации).

Для объекта из выборки, который находится в k-ом фолде, делается предсказание слабыми алгоритмами, которые были обучены на k-1 фолдах. Этот процесс итеративен и происходит для каждого фолда.

Создается набор прогнозов слабых алгоритмов для каждого объекта выборки.

На сформированных низкоуровневыми алгоритмами прогнозах в итоге обучается метамодель.

Рисунок 2

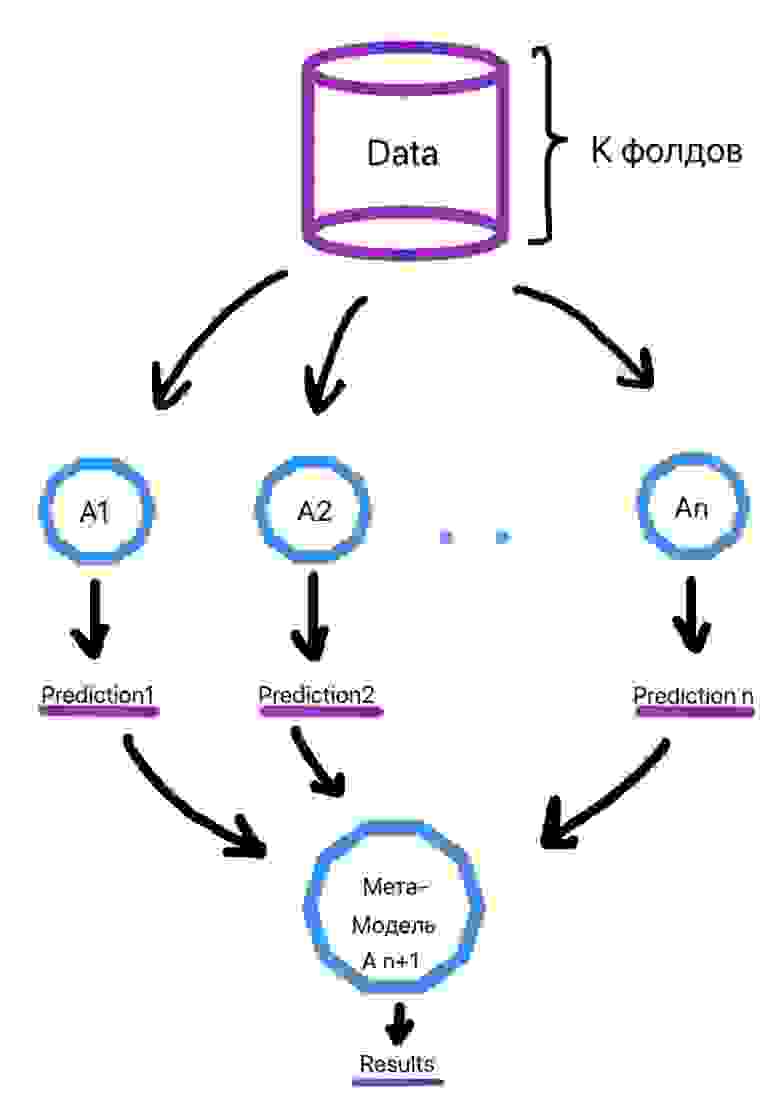
Ссылки на библиотеки для использования метода приведены ниже:

Бэггинг

Бэггинг является уже более популярным подходом и зачастую при упоминании этого термина вспоминается алгоритм построения случайного леса, как наиболее типичного его представителя.

При данном методе базовые алгоритмы являются представителями одного и того же семейства, они обучаются параллельно и почти независимо друг от друга, а финальные результаты лишь агрегируются. Нам необходимо, чтобы на вход слабым алгоритмам подавались разные данные, а не один и тот же набор, ведь тогда результат базовых моделей будет идентичен и смысла в них не будет.

0.632*n разных объектов. Таким образом, должны сформироваться m обучающих выборок для m слабых алгоритмов.

Бутстрэп выборки являются в значительной степени независимыми. Отчасти поэтому и говорят, что базовые алгоритмы обучаются на выборках независимо.

Что касается агрегации выходов базовых алгоритмов, то в случае задачи классификации зачастую просто выбирается наиболее часто встречающийся класс, а в случае задачи регрессии выходы алгоритмов усредняются (рис. 3). В формуле под ai подразумеваются выходы базовых алгоритмов.

Рисунок 3

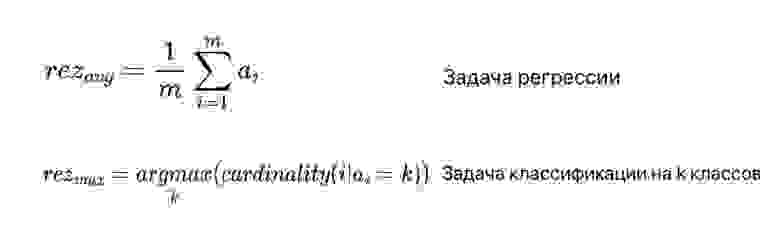
Общий процесс приведен на рисунке ниже (рис. 4):

Рисунок 4

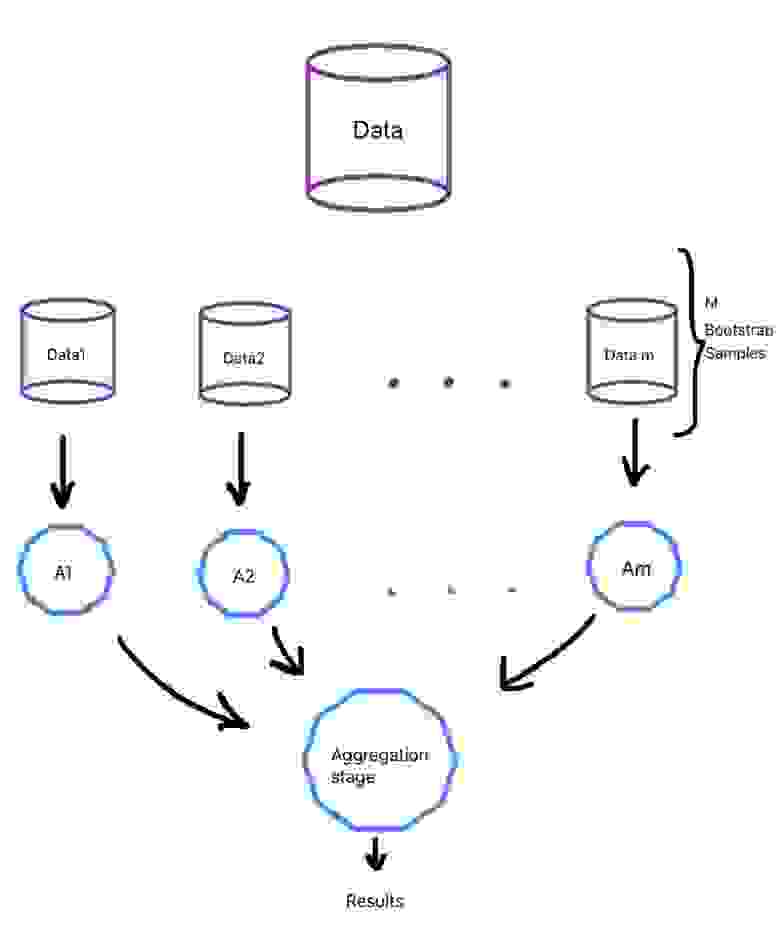
Случайный лес

Рисунок 5

Ссылки на библиотеки для использования метода приведены ниже:

Бустинг

В данном случае, модели уже не обучаются отдельно друг от друга, а каждая следующая правит ошибки предыдущей. То есть можно сказать, что если один слабый алгоритм не смог выявить какую-либо закономерность в данных, так как это было для него сложно, то следующая модель должна сделать это. Но из данного подхода вытекает недостаток: работу алгоритма трудно распараллелить из-за зависимости предыдущего и последующего шагов.

Бустинг направлен скорее на уменьшение смещения в данных, чем на снижение разброса в них. Поэтому в качестве базовых алгоритмов могут браться модели с достаточно высоким смещением, например, неглубокие случайные деревья.

Рисунок 6

Типичными представителями бустинга являются две модели: градиентный бустинг и AdaBoost. Обе по-разному решают одну и ту же оптимизационную задачу по поиску итоговой модели, представляющей собой взвешенную сумму слабых алгоритмов (рис. 6).

Градиентный бустинг использует типичный алгоритм градиентного спуска для решения задачи. Когда приходит время добавить новый слабый алгоритм в ансамбль делается следующее:

Находится оптимальный вектор сдвига, улучшающий предыдущий ансамбль алгоритмов.

Этот вектор сдвига является антиградиентом от функции ошибок работы предыдущего ансамбля моделей

Благодаря вектору сдвигов мы знаем, какие значения должны принимать объекты обучающей выборки

А поскольку нам надо найти очередной алгоритм в композиции, то находим тот, при использовании которого минимизируется отклонение ответов от истинных

Ссылки на библиотеки для использования метода приведены ниже:

Заключение

Таким образом, мы увидели, что для того, чтобы улучшить качество функционирования отдельно взятых моделей машинного обучения, существует ряд техник их объединения в ансамбли. Эти техники уже заложены в программные продукты и ими можно пользоваться, улучшая свое решение. Однако, с моей точки зрения, при решении задачи не стоит сразу же браться за них. Лучше сначала попробовать одну простую, отдельную модель, понять, как она функционирует на конкретных данных, а уже дальше использовать ансамбли.

Источник

Введение в машинное обучение

1.1 Введение

Благодаря машинному обучению программист не обязан писать инструкции, учитывающие все возможные проблемы и содержащие все решения. Вместо этого в компьютер (или отдельную программу) закладывают алгоритм самостоятельного нахождения решений путём комплексного использования статистических данных, из которых выводятся закономерности и на основе которых делаются прогнозы.

Технология машинного обучения на основе анализа данных берёт начало в 1950 году, когда начали разрабатывать первые программы для игры в шашки. За прошедшие десятилетий общий принцип не изменился. Зато благодаря взрывному росту вычислительных мощностей компьютеров многократно усложнились закономерности и прогнозы, создаваемые ими, и расширился круг проблем и задач, решаемых с использованием машинного обучения.

Чтобы запустить процесс машинного обучение, для начала необходимо загрузить в компьютер Датасет(некоторое количество исходных данных), на которых алгоритм будет учиться обрабатывать запросы. Например, могут быть фотографии собак и котов, на которых уже есть метки, обозначающие к кому они относятся. После процесса обучения, программа уже сама сможет распознавать собак и котов на новых изображениях без содержания меток. Процесс обучения продолжается и после выданных прогнозов, чем больше данных мы проанализировали программой, тем более точно она распознает нужные изображения.

Благодаря машинному обучению компьютеры учатся распознавать на фотографиях и рисунках не только лица, но и пейзажи, предметы, текст и цифры. Что касается текста, то и здесь не обойтись без машинного обучения: функция проверки грамматики сейчас присутствует в любом текстовом редакторе и даже в телефонах. Причем учитывается не только написание слов, но и контекст, оттенки смысла и другие тонкие лингвистические аспекты. Более того, уже существует программное обеспечение, способное без участия человека писать новостные статьи (на тему экономики и, к примеру, спорта).

1.2 Типы задач машинного обучения

Все задачи, решаемые с помощью ML, относятся к одной из следующих категорий.

1)Задача регрессии – прогноз на основе выборки объектов с различными признаками. На выходе должно получиться вещественное число (2, 35, 76.454 и др.), к примеру цена квартиры, стоимость ценной бумаги по прошествии полугода, ожидаемый доход магазина на следующий месяц, качество вина при слепом тестировании.

2)Задача классификации – получение категориального ответа на основе набора признаков. Имеет конечное количество ответов (как правило, в формате «да» или «нет»): есть ли на фотографии кот, является ли изображение человеческим лицом, болен ли пациент раком.

3)Задача кластеризации – распределение данных на группы: разделение всех клиентов мобильного оператора по уровню платёжеспособности, отнесение космических объектов к той или иной категории (планета, звёзда, чёрная дыра и т. п.).

4)Задача уменьшения размерности – сведение большого числа признаков к меньшему (обычно 2–3) для удобства их последующей визуализации (например, сжатие данных).

5)Задача выявления аномалий – отделение аномалий от стандартных случаев. На первый взгляд она совпадает с задачей классификации, но есть одно существенное отличие: аномалии – явление редкое, и обучающих примеров, на которых можно натаскать машинно обучающуюся модель на выявление таких объектов, либо исчезающе мало, либо просто нет, поэтому методы классификации здесь не работают. На практике такой задачей является, например, выявление мошеннических действий с банковскими картами.

1.3 Основные виды машинного обучения

Основная масса задач, решаемых при помощи методов машинного обучения, относится к двум разным видам: обучение с учителем (supervised learning) либо без него (unsupervised learning). Однако этим учителем вовсе не обязательно является сам программист, который стоит над компьютером и контролирует каждое действие в программе. «Учитель» в терминах машинного обучения – это само вмешательство человека в процесс обработки информации. В обоих видах обучения машине предоставляются исходные данные, которые ей предстоит проанализировать и найти закономерности. Различие лишь в том, что при обучении с учителем есть ряд гипотез, которые необходимо опровергнуть или подтвердить. Эту разницу легко понять на примерах.

Машинное обучение с учителем

Предположим, в нашем распоряжении оказались сведения о десяти тысячах московских квартир: площадь, этаж, район, наличие или отсутствие парковки у дома, расстояние от метро, цена квартиры и т. п. Нам необходимо создать модель, предсказывающую рыночную стоимость квартиры по её параметрам. Это идеальный пример машинного обучения с учителем: у нас есть исходные данные (количество квартир и их свойства, которые называются признаками) и готовый ответ по каждой из квартир – её стоимость. Программе предстоит решить задачу регрессии.

Ещё пример из практики: подтвердить или опровергнуть наличие рака у пациента, зная все его медицинские показатели. Выяснить, является ли входящее письмо спамом, проанализировав его текст. Это всё задачи на классификацию.

Машинное обучение без учителя

В случае обучения без учителя, когда готовых «правильных ответов» системе не предоставлено, всё обстоит ещё интереснее. Например, у нас есть информация о весе и росте какого-то количества людей, и эти данные нужно распределить по трём группам, для каждой из которых предстоит пошить рубашки подходящих размеров. Это задача кластеризации. В этом случае предстоит разделить все данные на 3 кластера (но, как правило, такого строгого и единственно возможного деления нет).

Если взять другую ситуацию, когда каждый из объектов в выборке обладает сотней различных признаков, то основной трудностью будет графическое отображение такой выборки. Поэтому количество признаков уменьшают до двух или трёх, и становится возможным визуализировать их на плоскости или в 3D. Это – задача уменьшения размерности.

1.4 Основные алгоритмы моделей машинного обучения

1. Дерево принятия решений

Это метод поддержки принятия решений, основанный на использовании древовидного графа: модели принятия решений, которая учитывает их потенциальные последствия (с расчётом вероятности наступления того или иного события), эффективность, ресурсозатратность.

Для бизнес-процессов это дерево складывается из минимального числа вопросов, предполагающих однозначный ответ — «да» или «нет». Последовательно дав ответы на все эти вопросы, мы приходим к правильному выбору. Методологические преимущества дерева принятия решений – в том, что оно структурирует и систематизирует проблему, а итоговое решение принимается на основе логических выводов.

2. Наивная байесовская классификация

Наивные байесовские классификаторы относятся к семейству простых вероятностных классификаторов и берут начало из теоремы Байеса, которая применительно к данному случаю рассматривает функции как независимые (это называется строгим, или наивным, предположением). На практике используется в следующих областях машинного обучения:

Всем, кто хоть немного изучал статистику, знакомо понятие линейной регрессии. К вариантам её реализации относятся и наименьшие квадраты. Обычно с помощью линейной регрессии решают задачи по подгонке прямой, которая проходит через множество точек. Вот как это делается с помощью метода наименьших квадратов: провести прямую, измерить расстояние от неё до каждой из точек (точки и линию соединяют вертикальными отрезками), получившуюся сумму перенести наверх. В результате та кривая, в которой сумма расстояний будет наименьшей, и есть искомая (эта линия пройдёт через точки с нормально распределённым отклонением от истинного значения).

Линейная функция обычно используется при подборе данных для машинного обучения, а метод наименьших квадратов – для сведения к минимуму погрешностей путем создания метрики ошибок.

4. Логистическая регрессия

Логистическая регрессия – это способ определения зависимости между переменными, одна из которых категориально зависима, а другие независимы. Для этого применяется логистическая функция (аккумулятивное логистическое распределение). Практическое значение логистической регрессии заключается в том, что она является мощным статистическим методом предсказания событий, который включает в себя одну или несколько независимых переменных. Это востребовано в следующих ситуациях:

Это целый набор алгоритмов, необходимых для решения задач на классификацию и регрессионный анализ. Исходя из того что объект, находящийся в N-мерном пространстве, относится к одному из двух классов, метод опорных векторов строит гиперплоскость с мерностью (N – 1), чтобы все объекты оказались в одной из двух групп. На бумаге это можно изобразить так: есть точки двух разных видов, и их можно линейно разделить. Кроме сепарации точек, данный метод генерирует гиперплоскость таким образом, чтобы она была максимально удалена от самой близкой точки каждой группы.

SVM и его модификации помогают решать такие сложные задачи машинного обучения, как сплайсинг ДНК, определение пола человека по фотографии, вывод рекламных баннеров на сайты.

Он базируется на алгоритмах машинного обучения, генерирующих множество классификаторов и разделяющих все объекты из вновь поступающих данных на основе их усреднения или итогов голосования. Изначально метод ансамблей был частным случаем байесовского усреднения, но затем усложнился и оброс дополнительными алгоритмами:

Кластеризация заключается в распределении множества объектов по категориям так, чтобы в каждой категории – кластере – оказались наиболее схожие между собой элементы.

Кластеризировать объекты можно по разным алгоритмам. Чаще всего используют следующие:

8. Метод главных компонент (PCA)

Метод главных компонент, или PCA, представляет собой статистическую операцию по ортогональному преобразованию, которая имеет своей целью перевод наблюдений за переменными, которые могут быть как-то взаимосвязаны между собой, в набор главных компонент – значений, которые линейно не коррелированы.

Практические задачи, в которых применяется PCA, – визуализация и большинство процедур сжатия, упрощения, минимизации данных для того, чтобы облегчить процесс обучения. Однако метод главных компонент не годится для ситуаций, когда исходные данные слабо упорядочены (то есть все компоненты метода характеризуются высокой дисперсией). Так что его применимость определяется тем, насколько хорошо изучена и описана предметная область.

9. Сингулярное разложение

В линейной алгебре сингулярное разложение, или SVD, определяется как разложение прямоугольной матрицы, состоящей из комплексных или вещественных чисел. Так, матрицу M размерностью [m*n] можно разложить таким образом, что M = UΣV, где U и V будут унитарными матрицами, а Σ – диагональной.

Одним из частных случаев сингулярного разложения является метод главных компонент. Самые первые технологии компьютерного зрения разрабатывались на основе SVD и PCA и работали следующим образом: вначале лица (или другие паттерны, которые предстояло найти) представляли в виде суммы базисных компонент, затем уменьшали их размерность, после чего производили их сопоставление с изображениями из выборки. Современные алгоритмы сингулярного разложения в машинном обучении, конечно, значительно сложнее и изощрённее, чем их предшественники, но суть их в целом нем изменилась.

10. Анализ независимых компонент (ICA)

Это один из статистических методов, который выявляет скрытые факторы, оказывающие влияние на случайные величины, сигналы и пр. ICA формирует порождающую модель для баз многофакторных данных. Переменные в модели содержат некоторые скрытые переменные, причем нет никакой информации о правилах их смешивания. Эти скрытые переменные являются независимыми компонентами выборки и считаются негауссовскими сигналами.

В отличие от анализа главных компонент, который связан с данным методом, анализ независимых компонент более эффективен, особенно в тех случаях, когда классические подходы оказываются бессильны. Он обнаруживает скрытые причины явлений и благодаря этому нашёл широкое применение в самых различных областях – от астрономии и медицины до распознавания речи, автоматического тестирования и анализа динамики финансовых показателей.

1.5 Примеры применения в реальной жизни

Пример 1. Диагностика заболеваний

Пациенты в данном случае являются объектами, а признаками – все наблюдающиеся у них симптомы, анамнез, результаты анализов, уже предпринятые лечебные меры (фактически вся история болезни, формализованная и разбитая на отдельные критерии). Некоторые признаки – пол, наличие или отсутствие головной боли, кашля, сыпи и иные – рассматриваются как бинарные. Оценка тяжести состояния (крайне тяжёлое, средней тяжести и др.) является порядковым признаком, а многие другие – количественными: объём лекарственного препарата, уровень гемоглобина в крови, показатели артериального давления и пульса, возраст, вес. Собрав информацию о состоянии пациента, содержащую много таких признаков, можно загрузить её в компьютер и с помощью программы, способной к машинному обучению, решить следующие задачи:

Пример 2. Поиск мест залегания полезных ископаемых

В роли признаков здесь выступают сведения, добытые при помощи геологической разведки: наличие на территории местности каких-либо пород (и это будет признаком бинарного типа), их физические и химические свойства (которые раскладываются на ряд количественных и качественных признаков).

Для обучающей выборки берутся 2 вида прецедентов: районы, где точно присутствуют месторождения полезных ископаемых, и районы с похожими характеристиками, где эти ископаемые не были обнаружены. Но добыча редких полезных ископаемых имеет свою специфику: во многих случаях количество признаков значительно превышает число объектов, и методы традиционной статистики плохо подходят для таких ситуаций. Поэтому при машинном обучении акцент делается на обнаружение закономерностей в уже собранном массиве данных. Для этого определяются небольшие и наиболее информативные совокупности признаков, которые максимально показательны для ответа на вопрос исследования – есть в указанной местности то или иное ископаемое или нет. Можно провести аналогию с медициной: у месторождений тоже можно выявить свои синдромы. Ценность применения машинного обучения в этой области заключается в том, что полученные результаты не только носят практический характер, но и представляют серьёзный научный интерес для геологов и геофизиков.

Пример 3. Оценка надёжности и платёжеспособности кандидатов на получение кредитов

С этой задачей ежедневно сталкиваются все банки, занимающиеся выдачей кредитов. Необходимость в автоматизации этого процесса назрела давно, ещё в 1960–1970-е годы, когда в США и других странах начался бум кредитных карт.

Лица, запрашивающие у банка заём, – это объекты, а вот признаки будут отличаться в зависимости от того, физическое это лицо или юридическое. Признаковое описание частного лица, претендующего на кредит, формируется на основе данных анкеты, которую оно заполняет. Затем анкета дополняется некоторыми другими сведениями о потенциальном клиенте, которые банк получает по своим каналам. Часть из них относятся к бинарным признакам (пол, наличие телефонного номера), другие — к порядковым (образование, должность), большинство же являются количественными (величина займа, общая сумма задолженностей по другим банкам, возраст, количество членов семьи, доход, трудовой стаж) или номинальными (имя, название фирмы-работодателя, профессия, адрес).

Для машинного обучения составляется выборка, в которую входят кредитополучатели, чья кредитная история известна. Все заёмщики делятся на классы, в простейшем случае их 2 – «хорошие» заёмщики и «плохие», и положительное решение о выдаче кредита принимается только в пользу «хороших».

Более сложный алгоритм машинного обучения, называемый кредитным скорингом, предусматривает начисление каждому заёмщику условных баллов за каждый признак, и решение о предоставлении кредита будет зависеть от суммы набранных баллов. Во время машинного обучения системы кредитного скоринга вначале назначают некоторое количество баллов каждому признаку, а затем определяют условия выдачи займа (срок, процентную ставку и остальные параметры, которые отражаются в кредитном договоре). Но существует также и другой алгоритм обучения системы – на основе прецедентов.

Источник

Открытый курс машинного обучения. Тема 5. Композиции: бэггинг, случайный лес

Пятую статью курса мы посвятим простым методам композиции: бэггингу и случайному лесу. Вы узнаете, как можно получить распределение среднего по генеральной совокупности, если у нас есть информация только о небольшой ее части; посмотрим, как с помощью композиции алгоритмов уменьшить дисперсию и таким образом улучшить точность модели; разберём, что такое случайный лес, какие его параметры нужно «подкручивать» и как найти самый важный признак. Сконцентрируемся на практике, добавив «щепотку» математики.

Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).

План этой статьи

1. Бэггинг

Из прошлых лекций вы уже узнали про разные алгоритмы классификации, а также научились правильно валидироваться и оценивать качество модели. Но что делать, если вы уже нашли лучшую модель и повысить точность модели больше не можете? В таком случае нужно применить более продвинутые техники машинного обучения, которые можно объединить словом «ансамбли». Ансамбль — это некая совокупность, части которой образуют единое целое. Из повседневной жизни вы знаете музыкальные ансамбли, где объединены несколько музыкальных инструментов, архитектурные ансамбли с разными зданиями и т.д.

Ансамбли

Хорошим примером ансамблей считается теорема Кондорсе «о жюри присяжных» (1784). Если каждый член жюри присяжных имеет независимое мнение, и если вероятность правильного решения члена жюри больше 0.5, то тогда вероятность правильного решения присяжных в целом возрастает с увеличением количества членов жюри и стремится к единице. Если же вероятность быть правым у каждого из членов жюри меньше 0.5, то вероятность принятия правильного решения присяжными в целом монотонно уменьшается и стремится к нулю с увеличением количества присяжных.
— количество присяжных
— вероятность правильного решения присяжного
— вероятность правильного решения всего жюри
— минимальное большинство членов жюри,
— число сочетаний из по

Давайте рассмотрим ещё один пример ансамблей — «Мудрость толпы». Фрэнсис Гальтон в 1906 году посетил рынок, где проводилась некая лотерея для крестьян.
Их собралось около 800 человек, и они пытались угадать вес быка, который стоял перед ними. Бык весил 1198 фунтов. Ни один крестьянин не угадал точный вес быка, но если посчитать среднее от их предсказаний, то получим 1197 фунтов.
Эту идею уменьшения ошибки применили и в машинном обучении.

Бутстрэп

Bagging (от Bootstrap aggregation) — это один из первых и самых простых видов ансамблей. Он был придуман Ле́о Бре́йманом в 1994 году. Бэггинг основан на статистическом методе бутстрэпа, который позволяет оценивать многие статистики сложных распределений.

Метод бутстрэпа заключается в следующем. Пусть имеется выборка размера . Равномерно возьмем из выборки объектов с возвращением. Это означает, что мы будем раз выбирать произвольный объект выборки (считаем, что каждый объект «достается» с одинаковой вероятностью ), причем каждый раз мы выбираем из всех исходных объектов. Можно представить себе мешок, из которого достают шарики: выбранный на каком-то шаге шарик возвращается обратно в мешок, и следующий выбор опять делается равновероятно из того же числа шариков. Отметим, что из-за возвращения среди них окажутся повторы. Обозначим новую выборку через . Повторяя процедуру раз, сгенерируем подвыборок . Теперь мы имеем достаточно большое число выборок и можем оценивать различные статистики исходного распределения.

Давайте для примера возьмем уже известный вам набор данных telecom_churn из прошлых уроков нашего курса. Напомним, что это задача бинарной классификации оттока клиентов. Одним из самых важных признаков в этом датасете является количество звонков в сервисный центр, которые были сделаны клиентом. Давайте попробуем визулизировать данные и посмотреть на распределение данного признака.

Как вы уже могли заметить, количество звонков в сервисный центр у лояльных клиентов меньше, чем у наших бывших клиентов. Теперь было бы хорошо оценить, сколько в среднем делает звонков каждая из групп. Так как данных в нашем датасете мало, то искать среднее не совсем правильно, лучше применить наши новые знания бутстрэпа. Давайте сгенерируем 1000 новых подвыборок из нашей генеральной совокупности и сделаем интервальную оценку среднего.

В итоге мы получили, что с 95% вероятностью среднее число звонков от лояльных клиентов будет лежать в промежутке между 1.40 и 1.50, в то время как наши бывшие клиенты звонили в среднем от 2.06 до 2.40 раз. Также ещё можно обратить внимание, что интервал для лояльных клиентов уже, что довольно логично, так как они звонят редко (в основном 0, 1 или 2 раза), а недовольные клиенты будут звонить намного чаще, но со временем их терпение закончится, и они поменяют оператора.

Бэггинг

Теперь вы имеете представление о бустрэпе, и мы можем перейти непосредственно к бэггингу. Пусть имеется обучающая выборка . С помощью бутстрэпа сгенерируем из неё выборки . Теперь на каждой выборке обучим свой классификатор . Итоговый классификатор будет усреднять ответы всех этих алгоритмов (в случае классификации это соответствует голосованию): . Эту схему можно представить картинкой ниже.

Рассмотрим задачу регрессии с базовыми алгоритмами . Предположим, что существует истинная функция ответа для всех объектов , а также задано распределение на объектах . В этом случае мы можем записать ошибку каждой функции регрессии

и записать матожидание среднеквадратичной ошибки

Средняя ошибка построенных функций регрессии имеет вид

Предположим, что ошибки несмещены и некоррелированы:

Построим теперь новую функцию регрессии, которая будет усреднять ответы построенных нами функций:

Найдем ее среднеквадратичную ошибку:

Таким образом, усреднение ответов позволило уменьшить средний квадрат ошибки в n раз!

Напомним вам из нашего предыдущего урока, как раскладывается общая ошибка:

Бэггинг позволяет снизить дисперсию (variance) обучаемого классификатора, уменьшая величину, на сколько ошибка будет отличаться, если обучать модель на разных наборах данных, или другими словами, предотвращает переобучение. Эффективность бэггинга достигается благодаря тому, что базовые алгоритмы, обученные по различным подвыборкам, получаются достаточно различными, и их ошибки взаимно компенсируются при голосовании, а также за счёт того, что объекты-выбросы могут не попадать в некоторые обучающие подвыборки.

Ошибка дерева решений

По графику и результатам выше видно, что ошибка дисперсии намного меньше при бэггинге, как мы и доказали теоретически выше.

Бэггинг эффективен на малых выборках, когда исключение даже малой части обучающих объектов приводит к построению существенно различных базовых классификаторов. В случае больших выборок обычно генерируют подвыборки существенно меньшей длины.

Следует отметить, что рассмотренный нами пример не очень применим на практике, поскольку мы сделали предположение о некоррелированности ошибок, что редко выполняется. Если это предположение неверно, то уменьшение ошибки оказывается не таким значительным. В следующих лекциях мы рассмотрим более сложные методы объединения алгоритмов в композицию, которые позволяют добиться высокого качества в реальных задачах.

Out-of-bag error

Забегая вперед, отметим, что при использовании случайных лесов нет необходимости в кросс-валидации или в отдельном тестовом наборе, чтобы получить несмещенную оценку ошибки набора тестов. Посмотрим, как получается «внутренняя» оценка модели во время ее обучения.

Каждое дерево строится с использованием разных образцов бутстрэпа из исходных данных. Примерно 37% примеров остаются вне выборки бутстрэпа и не используются при построении k-го дерева.

Это можно легко доказать: пусть в выборке объектов. На каждом шаге все объекты попадают в подвыборку с возвращением равновероятно, т.е отдельный объект — с вероятностью Вероятность того, что объект НЕ попадет в подвыборку (т.е. его не взяли раз): . При получаем один из «замечательных» пределов . Тогда вероятность попадания конкретного объекта в подвыборку .

Давайте рассмотрим, как это работает на практике:

На рисунке изображена оценка oob-ошибки. Верхний рисунок – это наша исходная выборка, ее мы делим на обучающую(слева) и тестовую(справа). На рисунке слева у нас есть сетка из квадратиков, которая идеально разбивает нашу выборку. Теперь нужно оценить долю верных ответов на нашей тестовой выборке. На рисунке видно, что наш классификатор ошибся в 4 наблюдениях, которые мы не использовали для обучения. Значит, доля верных ответов нашего классификатора:

Получается, что каждый базовый алгоритм обучается на

63% исходных объектов. Значит, на оставшихся

37% его можно сразу проверять. Out-of-Bag оценка — это усредненная оценка базовых алгоритмов на тех

37% данных, на которых они не обучались.

2. Случайный лес

Лео Брейман нашел применение бутстрэпу не только в статистике, но и в машинном обучении. Он вместе с Адель Катлер усовершенстовал алгоритм случайного леса, предложенный Хо, добавив к первоначальному варианту построение некоррелируемых деревьев на основе CART, в сочетании с методом случайных подпространств и бэггинга.

Решающие деревья являются хорошим семейством базовых классификаторов для бэггинга, поскольку они достаточно сложны и могут достигать нулевой ошибки на любой выборке. Метод случайных подпространств позволяет снизить коррелированность между деревьями и избежать переобучения. Базовые алгоритмы обучаются на различных подмножествах признакового описания, которые также выделяются случайным образом.
Ансамбль моделей, использующих метод случайного подпространства, можно построить, используя следующий алгоритм:

Алгоритм

Алгоритм построения случайного леса, состоящего из деревьев, выглядит следующим образом:

Итоговый классификатор , простыми словами — для задачи кассификации мы выбираем решение голосованием по большинству, а в задаче регрессии — средним.

Рекомендуется в задачах классификации брать , а в задачах регрессии — , где — число признаков. Также рекомендуется в задачах классификации строить каждое дерево до тех пор, пока в каждом листе не окажется по одному объекту, а в задачах регрессии — пока в каждом листе не окажется по пять объектов.

Таким образом, случайный лес — это бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков.

Сравнение с деревом решений и бэггингом

Как мы видим из графиков и значений ошибки MSE, случайный лес из 10 деревьев дает лучший результат, чем одно дерево или бэггинг из 10 деревьев решений. Основное различие случайного леса и бэггинга на деревьях решений заключается в том, что в случайном лесе выбирается случайное подмножество признаков, и лучший признак для разделения узла определяется из подвыборки признаков, в отличие от бэггинга, где все функции рассматриваются для разделения в узле.

Также можно увидеть преимущество случайного леса и бэггинга в задачах классификации.

На рисунках выше видно, что разделяющая граница дерева решений очень «рваная» и на ней много острых углов, что говорит о переобучении и слабой обобщающей способности. В то время как у бэггинга и случайного леса граница достаточно сглаженная и практически нет признаков переобучения.

Давайте теперь попробуем разобраться с параметрами, с помощью подбора которых мы cможем увеличить долю правильных ответов.

Параметры

Метод случайного леса реализован в библиотеке машинного обучения scikit-learn двумя классами RandomForestClassifier и RandomForestRegressor.

Полный список параметров случайного леса для задачи регрессии:

Для задачи классификации все почти то же самое, мы приведем только те параметры, которыми RandomForestClassifier отличается от RandomForestRegressor

Далее рассмотрим несколько параметров, на которые в первую очередь стоит обратить внимание при построении модели:

Рассмотрим применение случайного леса в реальной задаче

Для этого будем использовать пример с задачей оттока клиентов. Это задача классификации, поэтому будем использовать метрику accuracy для оценки качества модели. Для начала построим самый простой классификатор, который будет нашим бейслайном. Возьмем только числовые признаки для упрощения.

Получили долю верных ответов 91.21%, теперь попробуем улучшить этот результат и посмотреть, как ведут себя кривые валидации при изменении основных параметров.

Начнем с количества деревьев:

Как видно, при достижении определенного числа деревьев наша доля верных ответов на тесте выходит на асимптоту, и вы можете сами решить, сколько деревьев оптимально для вашей задачи.
На рисунке также видно, что на тренировочной выборке мы смогли достичь 100% точности, это говорит нам о переобучении нашей модели. Чтобы избежать переобучения, мы должны добавить параметры регуляризации в модель.

Параметр max_depth хорошо справляется с регуляризацией модели, и мы уже не так сильно переобучаемся. Доля верных ответов нашей модели немного возросла.

В данном случае мы не выигрываем в точности на валидации, но зато можем сильно уменьшить переобучение до 2% при сохранении точности около 92%.

В нашем случае оптимальное число признаков — 10, именно с таким значением достигается наилучший результат.

Мы рассмотрели, как ведут себя кривые валидации в зависимости от изменения основных параметров. Давайте теперь с помощью GridSearchCV найдем оптимальные параметры для нашего примера.

Вариация и декорреляционный эффект

Давайте запишем дисперсию для случайного леса как

где и – случайно выбранная пара деревьев на случайно выбранных объектах выборки
— это выборочная дисперсия любого произвольно выбранного дерева:

Легко спутать со средней корреляцией между обученными деревьями в данном случайном лесе, рассматривая деревья как N-векторы и вычисляя среднюю парную корреляцию между ними. Это не тот случай. Эта условная корреляция не имеет прямого отношения к процессу усреднения, а зависимость от в предупреждает нас об этом различии. Скорее является теоретической корреляцией между парой случайных деревьев, оцененных в объекте , которая была вызвана многократным сэмплированием обучающей выборки из генеральной совокупности , и после этого выбрана данная пара случайных деревьев. На статистическом жаргоне это корреляция, вызванная выборочным распределением и .

По факту, условная ковариация пары деревьев равна 0, потому что бустрэп и отбор признаков — независимы и одинаково распределены.

Если рассмотреть дисперсию по одному дереву, то она практически не меняется от переменных для разделения (), а вот для ансамбля это играет большую роль, и дисперсия для дерева намного выше, чем для ансамбля.
В книге The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani и Jerome Friedman) есть отличный пример, который это демонстрирует.

Смещение

Как и в бэггинге, смещение в случайном лесе такое же, как и смещение в отдельно взятом дереве :

Это также обычно больше (в абсолютных величинах), чем смещение «неусеченного» (unprunned) дерева, поскольку рандомизация и сокращение пространства выборки налагают ограничения. Следовательно, улучшения в прогнозировании, полученные с помощью бэггинга или случайных лесов, являются исключительно результатом уменьшения дисперсии.

Сверхслучайные деревья

В сверхслучайных деревьях (Extremely Randomized Trees) больше случайности в том, как вычисляются разделения в узлах. Как и в случайных лесах, используется случайное подмножество возможных признаков, но вместо поиска наиболее оптимальных порогов, пороговые значения произвольно выбираются для каждого возможного признака, и наилучший из этих случайно генерируемых порогов выбирается как лучшее правило для разделения узла. Это обычно позволяет немного уменьшить дисперсию модели за счет несколько большего увеличения смещения.

В библиотеке scikit-learn есть реализация ExtraTreesClassifier и ExtraTreesRegressor. Данный метод стоит использовать, когда вы сильно переобучаетесь на случайном лесе или градиентном бустинге.

Схожесть случайного леса с алгоритмом k-ближайших соседей

Метод случайного леса схож с методом ближайших соседей. Случайные леса, по сути, осуществляют предсказания для объектов на основе меток похожих объектов из обучения. Схожесть объектов при этом тем выше, чем чаще эти объекты оказываются в одном и том же листе дерева. Покажем это формально.

Рассмотрим задачу регрессии с квадратичной функцией потерь. Пусть — номер листа -го дерева из случайного леса, в который попадает объект . Ответ объекта равен среднему ответу по всем объектам обучающей выборки, которые попали в этот лист . Это можно записать так

Тогда ответ композиции равен

Видно, что ответ случайного леса представляет собой сумму ответов всех объектов обучения с некоторыми весами. Отметим, что номер листа , в который попал объект, сам по себе является ценным признаком. Достаточно неплохо работает подход, в котором по выборке обучается композиция из небольшого числа деревьев с помощью случайного леса или градиентного бустинга, а потом к ней добавляются категориальные признаки . Новые признаки являются результатом нелинейного разбиения пространства и несут в себе информацию о сходстве объектов.

Все в той же книге The Elements of Statistical Learning есть хороший наглядный пример сходства случайного леса и k-ближайших соседей.

Преобразование признаков в многомерное пространство

Все привыкли использовать случайный лес для задач обучения с учителем, но также есть возможность проводить обучение и без учителя. С помощью метода RandomTreesEmbedding мы можем сделать трансформацию нашего датасета в многомерное разреженное его представление. Его суть в том, что мы строим абсолютно случайные деревья, и индекс листа, в котором оказалось наблюдение, мы считаем за новый признак. Если в первый лист попал объект, то мы ставим 1, а если не попал, то 0. Так называемое бинарное кодирование. Контролировать количество переменных и также степень разреженности нашего нового представления датасета мы можем увеличивая/уменьшая количество деревьев и их глубины. Поскольку соседние точки данных скорее всего лежат в одном и том же листе дерева, преобразование выполняет неявную, непараметрическую оценку плотности.

3. Оценка важности признаков

Очень часто вы хотите понять свой алгоритм, почему он именно так, а не иначе дал определенный ответ. Или если не понять его полностью, то хотя бы какие переменные больше всего влияют на результат. Из случайного леса можно довольно просто получить данную информацию.

Суть метода

По данной картинке интуитивно понятно, что важность признака «Возраст» в задаче кредитного скоринга выше, чем важность признака «Доход». Формализуется это с помощью понятия прироста информации.

Если построить много деревьев решений (случайный лес), то чем выше в среднем признак в дереве решений, тем он важнее в данной задаче классификации/регрессии. При каждом разбиении в каждом дереве улучшение критерия разделения (в нашем случае неопределенность Джини(Gini impurity)) — это показатель важности, связанный с переменной разделения, и накапливается он по всем деревьям леса отдельно для каждой переменной.

Давайте немного углубимся в детали. Среднее снижение точности, вызываемое переменной, определяется во время фазы вычисления out-of-bag ошибки. Чем больше уменьшается точность предсказаний из-за исключения (или перестановки) одной переменной, тем важнее эта переменная, и поэтому переменные с бо́льшим средним уменьшением точности более важны для классификации данных. Среднее уменьшение неопределенности Джини (или ошибки mse в задачах регрессии) является мерой того, как каждая переменная способствует однородности узлов и листьев в окончательной модели случайного леса. Каждый раз, когда отдельная переменная используется для разбиения узла, неопределенность Джини для дочерних узлов рассчитывается и сравнивается с коэффициентом исходного узла. Неопределенность Джини является мерой однородности от 0 (однородной) до 1 (гетерогенной). Изменения в значении критерия разделения суммируются для каждой переменной и нормируются в конце вычисления. Переменные, которые приводят к узлам с более высокой чистотой, имеют более высокое снижение коэффициента Джини.

А теперь представим все вышеописанное в виде формул.

— предсказание класса перед перестановкой/удалением признака
— предсказание класса после перестановки/удаления признака

Заметим, что , если не находится в дереве

Расчет важности признаков в ансамбле:
— ненормированные

Пример

Рассмотрим результаты анкетирования посетителей хостелов с сайтов Booking.com и TripAdvisor.com. Признаки — средние оценки по разным факторам (перечислены ниже) — персонал, состояние комнат и т.д. Целевой признак — рейтинг хостела на сайте.

На рисунке выше видно, что люди больше всего обращают внимание на персонал и соотношение цена/качество и на основе впечатления от данных вещей пишут свои отзывы. Но разница между этими признаками и менее влиятельными признаками не очень значительная, и выкидывание какого-то признака приведет к уменьшению точности нашей модели. Но даже на основе нашего анализа мы можем дать рекомендации отелям в первую очередь лучше готовить персонал и/или улучшить качество до заявленной цены.

4. Плюсы и минусы случайного леса

Плюсы:
— имеет высокую точность предсказания, на большинстве задач будет лучше линейных алгоритмов; точность сравнима с точностью бустинга
— практически не чувствителен к выбросам в данных из-за случайного сэмлирования
— не чувствителен к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков, связано с выбором случайных подпространств
— не требует тщательной настройки параметров, хорошо работает «из коробки». С помощью «тюнинга» параметров можно достичь прироста от 0.5 до 3% точности в зависимости от задачи и данных
— способен эффективно обрабатывать данные с большим числом признаков и классов
— одинаково хорошо обрабатывет как непрерывные, так и дискретные признаки
— редко переобучается, на практике добавление деревьев почти всегда только улучшает композицию, но на валидации, после достижения определенного количества деревьев, кривая обучения выходит на асимптоту
— для случайного леса существуют методы оценивания значимости отдельных признаков в модели
— хорошо работает с пропущенными данными; сохраняет хорошую точность, если большая часть данных пропущенна
— предполагает возможность сбалансировать вес каждого класса на всей выборке, либо на подвыборке каждого дерева
— вычисляет близость между парами объектов, которые могут использоваться при кластеризации, обнаружении выбросов или (путем масштабирования) дают интересные представления данных
— возможности, описанные выше, могут быть расширены до неразмеченных данных, что приводит к возможности делать кластеризацию и визуализацию данных, обнаруживать выбросы
— высокая параллелизуемость и масштабируемость.

Минусы:
— в отличие от одного дерева, результаты случайного леса сложнее интерпретировать
— нет формальных выводов (p-values), доступных для оценки важности переменных
— алгоритм работает хуже многих линейных методов, когда в выборке очень много разреженных признаков (тексты, Bag of words)
— случайный лес не умеет экстраполировать, в отличие от той же линейной регрессии (но это можно считать и плюсом, так как не будет экстремальных значений в случае попадания выброса)
— алгоритм склонен к переобучению на некоторых задачах, особенно на зашумленных данных
— для данных, включающих категориальные переменные с различным количеством уровней, случайные леса предвзяты в пользу признаков с большим количеством уровней: когда у признака много уровней, дерево будет сильнее подстраиваться именно под эти признаки, так как на них можно получить более высокое значение оптимизируемого функционала (типа прироста информации)
— если данные содержат группы коррелированных признаков, имеющих схожую значимость для меток, то предпочтение отдается небольшим группам перед большими
— больший размер получающихся моделей. Требуется памяти для хранения модели, где — число деревьев.

5. Домашнее задание

Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.

В качестве закрепления материала предлагаем выполнить это задание – разобраться с бэггингом и обучить модели случайного леса и логистической регрессии для решения задачи кредитного скоринга. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).

6. Полезные источники

– Open Machine Learning Course. Topic 5. Bagging and Random Forest (перевод этой статьи на английский)
– Видеозапись лекции по мотивам этой статьи
– 15 раздел книги “Elements of Statistical Learning” Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
– Блог Александра Дьяконова
– Больше про практические применение случайного леса и других алгоритмов-композиций в официальной документации scikit-learn
– Курс Евгения Соколова по машинному обучению (материалы на GitHub). Есть дополнительные практические задания для углубления ваших знаний
– Обзорная статья «История развития ансамблевых методов классификации в машинном обучении» (Ю. Кашницкий)

Статья написана в соавторстве с yorko (Юрием Кашницким). Автор домашнего задания – vradchenko (Виталий Радченко). Благодарю bauchgefuehl (Анастасию Манохину) за редактирование.

Источник