критерий взаимной однозначности алфавитного кодирования

Элементы теории кодирования

Автор работы: Пользователь скрыл имя, 19 Января 2012 в 14:21, курсовая работа

Краткое описание

Содержание работы

Моя курсовая 2.doc

ify»> Исследованием и разработкой математических методов конфиденциальной информации, передаваемой отправителем получателю по общедоступным каналам связи, занимается криптология, одной из составляющих которой является криптография. Криптография разрабатывает методы защиты информации, т.е. представляет один из классов кодирования с целенаправленным изменением открытого текста, которое затрудняет получение содержащейся в нем конфиденциальной информации.

§ 2. Алфавитное кодирование

2. 1. Понятие алфавитного кодирования

В различных задачах, связанных с обработкой, передачей и хранением информации, а также в связи с потребностями техники возникает необходимость преобразования информации в более удобной форме. Кодирование, применяемое для этих целей, называется алфавитным кодированием. Алфавитное кодирование — это представление информации в стандартной форме, при которой элементарным синтаксическим единицам языка сообщений (буквам алфавита) последовательно сопоставляются кодовые комбинации символов из некоторого заданного алфавита. Под информацией здесь понимаем линейную последовательность букв (слова). Примером алфавитного кодирования может служить известный код Морзе (азбука Морзе), в котором слова кодируются побуквенно. А буквам сопоставляются слова в алфавите из трех символов <•, —, ˄>, где ˄ — пробел.

Другим примером алфавитного кодирования является десятичная система счисления.

В современных компьютерах в основном применяется двоичное кодирование, при котором любому символу исходного алфавита (буква, цифра, символы арифметических операций, специальные знаки и т. д.) ставится в соответствие их двоичный код. Кроме того, алфавитное кодирование применяется в криптологии для маскировки конфиденциальной информации.

2. 2. Математическое изучение алфавитного кодирования

Множество всех непустых слов конечной длины в алфавите А обозначим через А*.

Если S — подмножество множества А*, то слова из S называются сообщениями, а объект, порождающий слова из S, — источником сообщений. Источником сообщений может быть человек, автомат и т. д.

Пусть, кроме алфавита А, задан еще алфавит В = ₁, b₁,…, b_т>. Зададим отображение f, которое каждому слову α ϵ S ставит в соответствие словоβϵ В*, где В* — множество всех непустых слов конечной длины в В.

Слово β будем называть кодом сообщения α, а процесс перехода от слова α к слову β — кодированием.

Схема, определяющая отображение f на буквах алфавита А, называется схемой кодирования, обозначается ∑ и оформляется в виде таблицы:

2. 3. Проблема взаимной однозначности

Одним из основных вопросов в кодировании является проблема взаимной однозначности, т. е. возможность по коду β сообщения α однозначно восстановить α.

Возникает вопрос: возможно ли по схеме алфавитного кодирования узнать, обладает ли алфавитное кодирование свойством однозначности или нет? Если решать эту задачу, исходя из определения, то нужно перебрать бесконечное число слов, так как для каждого кода нужно установить, допускает или не допускает этот код однозначное кодирование.

2. 4. Достаточный признак взаимной однозначности алфавитного кодирования

Прежде, чем устанавливать общий критерий взаимной однозначности алфавитного кодирования, приведём простой достаточный признак взаимной однозначности.

Введем следующие понятия.

Если β = β҆ β”, то β҆ называется началом, или постфиксом, слова β.

Если β҆ ≠ ˄, то β҆ называется собственным началом.

Если β” ≠˄, то β” называется собственным окончанием слова β.

Определение: алфавитного кодирования обладает свойствами префикса, если ни один элементарный код не является префиксом другого элементарного кода.

Теорема 1: Если схема ∑ алфавитного кодирования обладает свойством префикса, то алфавитное кодирование взаимно однозначно.

Доказательство: Допустим, что некоторое слово β ϵ В* допускает два декодирования. Это значит, что β можно представить в двух видах: β₁ = β_i1 β_i2 … β_ik; β₂ = β_j1 β_j2 … β_jl.

Так как эти представления различны, то существует такое р, что 1 ≤ р ≤ min(k, l), для которого β_ip ^ β_ip. Но тогда одно из слов β₁ и β₂ есть префикс другого. Это противоречит условию теоремы. Следовательно, наше утверждение о существовании двух декодирований неверно. Теорема доказана.

Заметим, что условие префиксности не является необходимым, т. е. другими словами, схема алфавитного кодирования может не обладать свойствами префиксности, но алфавитное кодирование, задаваемое этой схемой, будет взаимно однозначным.

2. 5. Общий критерий взаимной однозначности

Для вывода общего критерия взаимной однозначности понадобится
следующее понятие.

Представление элементарного кода Р; схемы алфавитного кодирова-
ния ∑ в виде β_i = β҆ β_i1… β_ik β”, где слово β҆ не может оканчиваться на элементарный код, а слово Р» начинаться с элементарного кода, будем называть нетривиальным разложением элементарного кода. При этом одно из слов β҆ или β” может быть пустым (˄).

Для определения однозначности или неоднозначности схемы алфавитного кодирования существует эффективный алгоритм, использующий понятие нетривиального разложения элементарных кодов.
Опишем этот алгоритм.

6. По разложениям, полученным в пункте 5, строится ориентиро-
ванный граф G_∑ следующим образом. Вершины графа отождествляют с
элементами множества М. Пара вершин β’ и β» соединяются ориентиро-
ванными ребрами в том и только в том случае, если существует разло-
жение β’β_i1…β_ikβ». При этом ребру (β’,β») приписывается слово β_i1…β_ik,
соответствующее этому разложению.

7. По полученному графу G_∑ легко проверить, обладает или нет исход-
ная схема кодирования свойством взаимной однозначности.

Справедлива следующая теорема.

Теорема 3: Алфавитное кодирование со схемой ∑ не обладала свойством взаимной однозначности тогда и только тогда, когда граф G_∑ содержит ориентированный цикл (контур), проходящий через вершину ˄. Т.е. алфавитное кодирование является взаимно однозначным тогда и только тогда, когда в графе G_∑ отсутствуют контуры и петли, проходящие через вершины ˄.

Замечание: Напомним, что если схема алфавитного кодирования ∑ не обладает свойством взаимной однозначности, то это означает, что существуют слова из В*, допускающие два кодирования. Одно из таких слов β легко находится по графу _∑.

Для записи слова β нужно посмотреть ориентированный цикл, проходящий через вершину ˄, начиная с ˄, и выписать последовательно все слова, приписанные ребрам и вершинам, входящим в этот цикл.

§ 3. Двоичный алфавит

3. 1. Понятие двоичного алфавита

В современных компьютерах любая информация представляется в виде двоичных кодов, т. е. упорядоченных наборов двух различных символов, которые обычно обозначаются через 0 и 1. Таким образом, алфавит, в котором записываются сообщения, считаем состоящим из двух символов <0,1>. Он называется двоичным алфавитом.

Тогда сообщение есть конечная последовательность символов этого алфавита.

Это простейшее алфавитное кодирование, которое является взаимнооднозначным, так как каждому символу исходного алфавита ставится в соответствие определенное двоичное число.

Например, натуральному числу 23 соответствует двоичное число 10111,поскольку

23 = 1 • 2 4 + 0 • 2 3 + 1 • 2 2 + 1 • 2 1 + 1 • 2°.

Полезно запомнить запись в двоичной системе первых шестнадцати натуральных чисел

Источник

Элементы теории кодирования

Автор работы: Пользователь скрыл имя, 19 Января 2012 в 14:21, курсовая работа

Краткое описание

Содержание работы

Моя курсовая 2.doc

Число Х₁₀ называется нормализованным, если оно представлено в виде

М₁₀ – мантисса нормализованного числа, k – порядок нормализованного числа. Очевидно, что первая значащая цифра мантиссы всегда ненулевая

Задача. Представить в нормализованном виде числа: 1234, 0,03456

При нормализации происходит установление его составляющих элементов:

Аналогично нормализации десятичного числа можно в нормализованной форме представить и число в произвольной системе счисления q:

§ 5. Решение практических задач

Тема «Алфавитное кодирование»

Выясните, обладает ли эта схема кодирования свойством однозначности.

Решение. Процесс декодирования осуществляется следующим образом: код β слова α разбивается на элементарные коды. Для этого в слове β последовательно находятся все буквы b₂ и затем выделяются пары bb₂, каждая такая пара соответствует букве a₂. Оставшиеся буквы b₁ соответствуют букве a₁.

Задача 2. Пусть схема ∑ задана следующей таблицей

Покажите, что эта схема не обладает свойством однозначности.

Это слово допускает два декодирования.

Следовательно, схема ∑ не обладает свойством однозначности.

Задача 3. Схема алфавитного кодирования задана таблицей

оставшиеся буквы b₁ заменяем на a₁ . В результате получим исходное сообщение (слово) α.

Задача 4. Алфавитное кодирование задано схемой ∑ в виде таблицы

С помощью общего критерия взаимной однозначности выясните, обладает ли эта схема кодирования свойством взаимной однозначности или нет.

Решение. Алгоритм решения.

Задача 5. Схема алфавитного кодирования задана таблицей

Источник

Обработка сообщений как кодирование

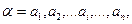
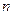
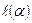
Основные понятия теории кодирования. Словом в алфавите А называется кортеж, т.е. любая конечная последовательность символов где , число показывает длину слова и обозначается .Пустое слово обозначается L, т.е. если L , то = .

Для слова буква a₁ называется началом или префиксом слова , а буква – окончанием или постфиксом слова . Пустое слово является началом и окончанием любого слова , если . Для того, чтобы соединить слова, необходимо, чтобы префикс второго слова следовал сразу за постфиксом первого. Соединение слов a₁ и a₂ обозначается a₁a₂, соединение n одинаковых слов a обозначается , причем . Множество всех непустых слов алфавита A обозначим A*, т.е. A*=<a|l(a)>0>, в алфавите В – B*. Множество A называют алфавитом сообщений, а множество B – кодирующим алфавитом.

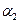
Блочно-двоичный (m,n)-код.Слово длины m записывается с помощью двоичных символов 0 и 1. Сообщение длины m кодируется другим словом длины n, где m

Для установления, обладает ли заданный код свойством однозначности, будем применять алгоритм:

1) Выпишем все нетривиальные разложения каждого элементарного кода.
2) Составим множество M₁, включая в него слова, входящие в качестве начал (префиксов) в нетривиальные разложения элементарных кодов.

3) Составим множество M₂, включая в него слова, которые являются окончаниями (постфиксами) нетривиальных разложений элементарных кодов.

4) Составим множество , которое состоит из множества начал, окончаний нетривиальных разложений элементарных кодов.

5) Выпишем все разложения элементарных кодов, связанных с элементами множества M.

6) По полученным разложениям построим ориентированный граф, вершины которого – элементы множества . Пару вершин соединяем дугами тогда и только тогда, когда существует разложения, в которое вершины графа входят в качестве начала и конца.

7) Граф G подскажет, обладает ли заданная схема свойством однозначности. Для ответа на этот вопрос воспользуемся теоремой А.А. Маркова.

Алфавитное кодирование с разделимой схемой допускает декодирование. Для разделимой схемы алфавитного кодирования существует так называемая средняя цена или длина кодирования , которая обозначаетсяи определяется где – длина кодового слова, а – вероятность появления буквы .

Произвольное отображение множества A во множество слов алфавита B называют двоичным кодированием множества A. Код называется равномерным, если все буквы его алфавита имеют одинаковую длину.

Методы эффективного кодирования информации.Наиболее выгодным является кодирование, на которое затрачивается минимальное количество символов (букв алфавита).

Алфавитное разделяемое кодирование будет кодированием с минимальной избыточностьюили оптимальным, если будут учтены распределения вероятностей p для символов этого алфавита.

Оптимальное кодирование. Последовательные появления букв алфавита А статистически независимы и подчинены распределению вероятностей .

Каждый код b в алфавите В = <0, 1>характеризуется средним числом двоичных цифр, приходящихся на одну букву алфавита А при побуквенном кодировании.

Источник

Алфавитное кодирование

Автор работы: Пользователь скрыл имя, 09 Декабря 2011 в 08:53, курсовая работа

Краткое описание

Работа подавляющего числа современных систем связи основана на передаче сообщений в цифровом виде. Сбой при приеме любого элемента цифровых данных способен вызвать значительное искажение всего сообщения в целом, что, в свою очередь, может привести к полной потере информации, содержащейся в нем. В современных информационных системах важнейшей задачей является обеспечение информационной безопасности, связанной с методами криптографии и кодирования, теоретические основы которой заложил Шеннон в своих трудах.

Содержание работы

Введение 3
1. Теоретические основы задачи кодирования……………………………………………. 6
1.1. Постановка задачи кодирования………….……………………………..….……………6
1.2. Первая теорема Шеннона……………………………………………………………. 10
1.3. Вторая теорема Шеннона……………………………………………………………….13
1.4. Помехоустойчивые коды…. …………………………………………. …….…14
2. Алфавитное кодирование. 17
2.1. Основные определения. 17
2.2. Проблема распознавания взаимной однозначности алфавитного кодирования. 18
2.3. Алгоритм построения префиксного кода по набору длин элементарных кодов. 22
2.4. Алгоритмы экономного алфавитного кодирования. 23
2.4.1. Алгоритм Хаффмана. 24
2.4.2. Алгоритм Фано. 26
2.4.3. Алгоритм Шеннона. 27
2.4.4. Энтропия и ее связь со стоимостью оптимального алфавитного
кодирования. 28
2.4.5. Возможности сжатия при алфавитном кодировании, учитывающем
синтаксис языка сообщений. 31
Заключение. 34
Список литературы 35

Алфавитное кодирование.doc

В настоящее время темпы развития телекоммуникационных систем стали предпосылкой для появления принципиально новых способов кодирования сообщений. Причем одной из задач кодирования стало не только достоверная передача, но и быстрая обработка данных. Несмотря на рост мощности вычислительной техники, актуальным остается вопрос построения простых алгоритмов коррекции ошибок. Одним из малоизученных направлений в этой области можно считать использование кодов с иррациональным основанием.

Высокоэффективным средством решения данной проблемы является применение помехоустойчивого кодирования, основанного на введении искусственной избыточности в передаваемое сообщение. Теория и техника помехоустойчивого кодирования прошли несколько этапов в своем развитии. Изначально это было просто эмпирическое использование простейших кодов с повторением, с постоянным весом, с одной проверкой на четность и т.д. В дальнейшем теория помехоустойчивого кодирования прошла довольно длинный путь развития, в процессе которого для ее создания использовались основы математической теории – ответвления высшей алгебры и теории чисел с приложением к реальным системам связи.

Следует отметить тот факт, что хотя существующие на данный момент системы передачи данных отвечают всем основным стандартам и требованиям, они все же не являются совершенными. Причин тому влияние помех в канале связи. Одним из средств решения подобных несоответствий в системах передачи цифровой информации, является применение помехоустойчивых кодов, лежащих в основе устройств кодирования/декодирования.

Помехоустойчивое кодирование передаваемой информации позволяет в приемной части системы обнаруживать и исправлять ошибки. Коды, применяемые при помехоустойчивом кодировании, называются корректирующими кодами. Как правило, корректирующий код может исправлять меньше ошибок, чем обнаруживать. Число ошибок, которые корректирующий код может исправить в определенном интервале последовательности двоичных символов, например, в одной кодовой комбинации, называется исправляющей способностью кода.

2. Алфавитное кодирование

Чтобы сделать кодирование объектом математической теории, на модель канала связи накладываются дополнительные ограничения. Основным объектом, который систематически изучается, является алфавитное кодирование – простейший вид автоматного кодирования, при котором память не используется.

2.1. Основные определения.

Рассмотрим вопрос об условиях взаимной однозначности кодирования слов некоторого алфавита при помощи замены каждой буквы некоторым словом того же или какого-либо другого алфавита. Докажем, что в общем случае задача сводится к аналогичной задаче для случая кодирования той же системой слов конечного множества слов этого алфавита. Установим необходимое и достаточное условие взаимной однозначности, а, следовательно, и возможности обращения оператора, осуществляющего кодирование.

Требование инъективности отображения f означает, что различные сообщения должны

кодироваться разными двоичными последовательностями. При выполнении этого

требования обеспечивается однозначность декодирования сообщений. Такое кодирование называется взаимно-однозначным.

В теории кодирования рассматриваются не любые инъективные отображения f, а те из них, которые могут быть реализованы алгоритмами.

Наиболее изученными являются вопросы экономного кодирования для случая, когда

L=B*, свойства информации описываются вероятностями появления букв в сообщениях

из B*, а в качестве способа кодирования применяется побуквенное, или алфавитное,

Алфавитное кодирование задается схемой, в которой каждой букве алфавита ставится в соответствие двоичная последовательность символов:

При построении схемы кодирования используется дополнительная информация о вероятностях появления букв – вероятностное распределение P = (p₁,p₂,…p_m).

При построении схем алфавитного кодирования возникают две основные задачи:

2.2. Проблема распознавания взаимной однозначности алфавитного кодирования

Пример 2.1. Рассмотрим схему

f ₁ задает взаимно-однозначное кодирование. Достаточно заметить, что перед каждым вхождением символа 1 стоит символ 0, поэтому каждое вхождение 1 вместе с предшествующим нулем кодирует букву b₂. Символ 0, за которым не следует 1, кодирует

букву b₁. Например, последовательность β = 001010001 имеет единственную

Пример 2.2. Рассмотрим схему

Для непосредственной проверки взаимной однозначности необходимо в общем случае

проверить бесконечное множество пар слов.

Определение 2.1. Пусть слово α имеет вид α₁α₂. Тогда α₁ называется префиксом слова α, а α₂ — суффиксом α. Если 0

Определение 2.2. Схема алфавитного кодирования f обладает свойством префикса,

если для любых i и j (1 ≤ i, j ≤ m, i ≠ j) элементарный код v_i не является префиксом

Определение 2.3. Алфавитное кодирование, схема которого обладает свойством префикса, называется префиксным.

Теорема 2.1. Если схема обладает свойством префикса, то алфавитное кодирование является взаимно-однозначным.

Таким образом, свойство префикса является достаточным условием взаимной однозначности.

Теорема 2.2. Если алфавитное кодирование со схемой f обладает свойством взаимной

кода со схемой f, но не достаточным.

Мак-Миллана, то существует префиксное кодирование, удовлетворяющее равенствам:

Следствие. Если существует взаимно-однозначное алфавитное кодирование с заданными длинами элементарных кодов, то существует также префиксное кодирование с теми же длинами элементарных кодов.

как достаточное условие взаимной однозначности, в том смысле, что если неравенство для некоторой схемы кодирования выполняется, можно заменить эту схему схемой со свойством префикса с теми же длинами элементарных кодов.

Пусть задан код V = (v₁,v₂,…v_m). Элементарные коды определяют бинарное кодовое дерево. Из каждой вершины дерева выходит не более двух ребер в вершины следующего яруса, левое из которых помечается символом 0, а правое – символом 1. Элементарным

кодам соответствуют вершины дерева, определяемые путем, идущим от корня. Если код префиксный, элементарные коды расположены в листьях дерева.

Дерево называется насыщенным, если из каждой вершины, не являющейся листом, в

следующий ярус выходит ровно два ребра.

На рис. 2.1 изображено дерево для схемы префиксного кодирования f₃.

Рис.2.1. Кодовое дерево для схемы кодирования f₃.

Проблема распознавания взаимной однозначности алфавитного кодирования решена

Ал. А. Марковым (1963 г.). Алгоритм распознавания состоит в следующем.

Источник