Научная литература 

Можно ли утверждать что число 60 кратное числа 10

admin 0 Comments

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

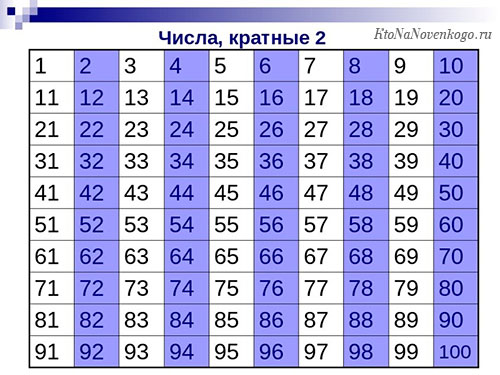
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

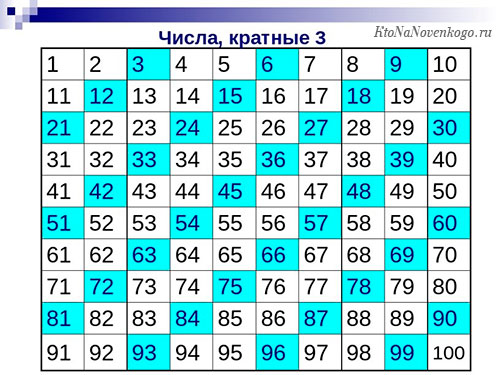
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

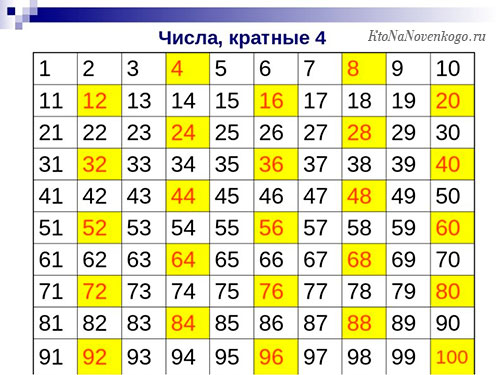
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

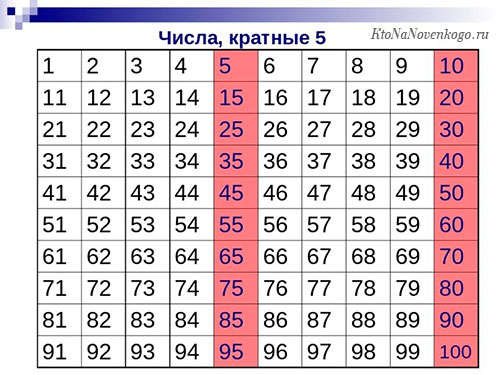
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

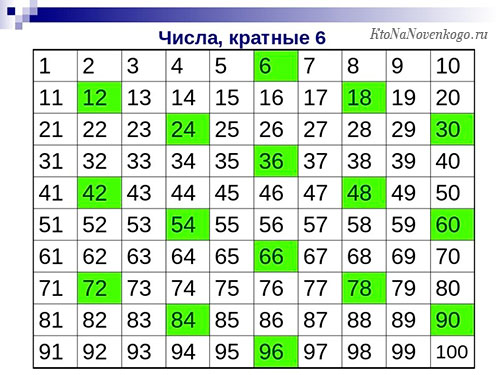
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

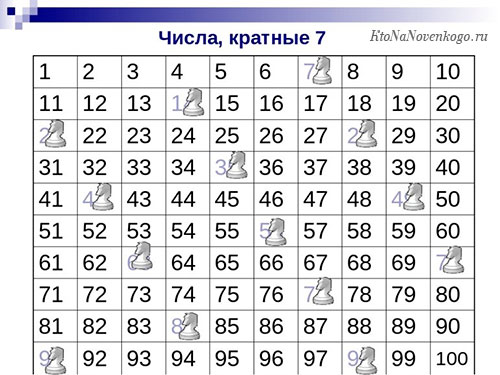
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Числа, кратные 9271985 8773 81611772
Сумма918271899

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Какие числа кратны 10

Содержание статьи

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Термин «кратность» относится к области математики: с точки зрения этой науки, он означает количество раз, которое определенное число входит в состав другого числа.

Понятие кратности

Второе важное свойство касается определения наименьшего целого числа, являющегося кратным рассматриваемому. Так, наименьшим кратным по отношению к любому числу является само это число. Это связано с тем, что наименьшим целым результатом деления одного числа на другое является единица, а именно деление числа само на себя и обеспечивает этот результат. Соответственно, число, кратное рассматриваемому, не может быть меньше, чем само это число. Например, для числа 3 наименьшим кратным числом будет 3. При этом определить наибольшее число, кратное рассматриваемому, фактически невозможно.

Числа, кратные 10

Числа, кратные 10, обладают всеми перечисленными свойствами наравне с другими кратными числами. Так, из перечисленных свойств следует, что наименьшим числом, кратным 10, является само число 10. При этом, поскольку число 10 является двузначным, можно сделать вывод, что кратным числу 10 могут быть только числа, состоящие не менее чем из двух знаков.

Для того чтобы получить другие числа, кратные 10, необходимо число 10 умножить на любое целое положительное число. Таким образом, в перечень чисел, кратных 10, войдут числа 20, 30, 40, 50 и так далее. Следует обратить внимание, что все полученные числа должны без остатка делиться на 10. При этом определить наибольшее число, кратное 10, как и в случаях с другими числами, невозможно.

Кроме того, обратите внимание, что существует простой практический способ определить, является ли конкретное рассматриваемое число кратным 10. Для этого следует выяснить, какова его последняя цифра. Так, если она равна 0, рассматриваемое число будет кратным 10, то есть может быть без остатка разделено на 10. В противном случае число не является кратным 10.

Источник

Мерзляк 6 класс — § 6. Наименьшее общее кратное

Вопросы к параграфу

1. Какое число называют наименьшим общим кратным двух чисел?

Наименьшее общее кратное (НОК) двух чисел — это число, которое делится нацело на каждое из этих двух чисел и, при этом, является наименьшим из всех чисел, удовлетворяющих данному условию.

2. Как можно найти НОК двух натуральных чисел, используя их разложения на простые множители?

Чтобы найти наименьшее общее кратное (НОК) надо:

Полученное число и будет НОК двух данных чисел.

Например найдём наименьшее общее кратное для чисел 45 и 24, используя данное правило:

1. Разложим оба числа на простые множители и представить его в виде произведения степеней.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

2. Выбрать степени, основания которых встречаются только в одном из разложений заданных чисел на простые множители.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

3. Из каждой пары степеней с одинаковыми основаниями выбрать степень с наибольшим показателем.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

4. Перемножить выбранные степени.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Значит наименьшее общее кратное чисел 45 и 24 равно 360.

Ответ: НОК (45, 24) = 360.

3. Чему равно наименьшее общее кратное двух чисел, одно из которых является делителем другого?

Если из двух чисел одно является делителем другого, то наименьшее общее кратное (НОК) равно большему числу.

4. Чему равно наименьшее общее кратное взаимно простых чисел?

Наименьшее общее кратное двух взаимно простых чисел равно их произведению.

Решаем устно

1. Назовите какое-либо трёхзначное число, которое:

1) делится нацело на 3, но не делится нацело на 9

111, 273 и т.д. — сумма чисел такого числа должна делиться на 3, но не должна делиться на 9.

2) делится нацело на 9 и на 2

180, 324, 162 — это должно быть чётное число, сумма цифр которого делится нацело на 9.

3) делится нацело на 9 и на 5

450, 315 — это должно быть число, оканчивающееся на 0 или на 5, при этом сумма его цифр должна делиться на 9.

4) делится нацело на 3 и на 4

600, 228, 516 — это должно быть число оканчивающееся на 00 или на двузначное число, которое делится на 4, при этом сумма чисел этого числа должна делиться на 3.

5) делится нацело на 9, а при делении на 10 даёт остаток 7.

927, 657 — это должно быть число, сумма чисел которого делиться нацело на 9, а само число оканчивается на цифру 7.

2. Назовите три общих кратных чисел:

1) 2 и 3

Кратными и числа 2, и числа 3, являются числа: 6, 12, 18 и т.д.

2) 4 и 6

3) 5 и 10

Кратными и числа 5, и числа 10, являются числа: 10, 20, 30 и т.д.

3. Используя цифры 0, 2, 3 и 4, составьте наименьшее и наибольшее четырёхзначные числа, кратные 5. Можно ли утверждать, что полученные числа кратны 15?

4. В парке посадили каштаны и дубы, причём на каждый каштан приходилось три дуба. Сколько всего деревьев посадили в парке, если дубов посадили 24?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

1) 24 : 3 = 8 (шт) — каштанов посадили в парке.

2) 24 + 8 = 32 (шт) — деревьев посадили в парке.

Упражнения

163. Найдите наименьшее общее кратное чисел:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

164. Найдите наименьшее общее кратное чисел:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

165. Найдите наибольший общий делитель и наименьшее общее кратное чисел а и b:

1) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОД (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОК (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

2) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОД (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОК (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

166. Найдите наибольший общий делитель и наименьшее общее кратное чисел а и b:

1) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОД (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОК (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

2) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОД (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

НОК (a, b) = Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

167. Найдите наименьшее общее кратное чисел:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

168. Найдите наименьшее общее кратное чисел:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

169. Найдите наименьшее общее кратное знаменателей дробей:

1) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Знаменатель первой дроби равен 12, а второй — 15. Значит надо найти НОК (12, 15):

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: Наименьшее общее кратное знаменателей дробей равно 60.

2) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Знаменатель первой дроби равен 100, а второй — 125. Значит надо найти НОК (100, 125):

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: Наименьшее общее кратное знаменателей дробей равно 600.

170. Найдите наименьшее общее кратное знаменателей дробей:

1) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Знаменатель первой дроби равен 9, а второй — 6. Значит надо найти НОК (9, 6):

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: Наименьшее общее кратное знаменателей дробей равно 18.

2) Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10и Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Знаменатель первой дроби равен 20, а второй — 25. Значит надо найти НОК (20, 25):

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: Наименьшее общее кратное знаменателей дробей равно 100.

171. Найдите наименьшее общее кратное:

1) первых пяти натуральных чисел

Первые пять натуральных чисел — это 1, 2, 3, 4, 5. Разложим их на простые множители:

НОК (1, 2, 3, 4, 5) = 2² • 3 • 5 = 4 • 15 = 60

2) первых пяти нечётных чисел

Первые пять нечётных чисел — это 1, 3, 5, 7, 9. Разложим их на простые множители:

НОК (1, 3, 5, 7, 9) = 3² • 5 • 7 = 9 • 35 = 315

3) первых пяти простых чисел

Первые пять простых чисел — это 2, 3, 5, 7, 11. Мы знаем, что единственным простым множителем простого числа является само это число. Значит:

НОК (2, 3, 5, 7, 11) = 2 • 3 • 5 • 7 • 11= 2 310

172. Найдите наименьшее общее кратное:

1) первых пяти чётных чисел

Первые пять чётных чисел — это 2, 4, 6, 8, 10. Разложим их на простые множители:

НОК (2, 4, 6, 8, 10) = 2³ • 3 • 5 = 8 • 15 = 120

2) первых четырёх составных чисел

Первые четыре составные числа — это 4, 6, 8, 9. Разложим их на простые множители:

НОК (4, 6, 8, 9) = 2³ • 3² = 8 • 9 = 72

173. Длина шага Чебурашки равна 15 см, а крокодила Гены — 50 см. Какое наименьшее одинаковое расстояние должен пройти каждый из них, чтобы они оба сделали по целому числу шагов?

Для того, чтобы найти нужное расстояние, надо найти число, которое делится и на 15, и на 50 — НОК (15, 50). Разложим эти числа на простые множители:

НОК (15, 50) = 2 • 3 • 5² = 6 •25 = 150.

Значит Чебурашке и крокодилу Гене надо пройти 150 см.

174. С одного места в одном направлении но велотреку одновременно стартовали два велосипедиста. Один из них делает круг за 1 мин, а другой — за 45 с. Через какое наименьшее количество минут после начала движения они вновь окажутся н месте старта? Сколько кругов по велотреку при этом сделает каждый из них?

1 минута = 60 секунд

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Значит они вновь окажутся вместе через 180 секунд.

Найдём, сколько кругов по велотреку сделает каждый из велосипедистов:

Ответ: они встретятся через 180 секунд, первый велосипедист сделает 3 круга, а второй — 4 круга.

175. Дима п Петя отправились в поход из одного пункта в одном направлении. Петя делал остановку для отдыха через каждые 2 400 м, а Дима — через каждые 2 800 м. На каком наименьшем расстоянии от пункта отправления места их остановок совпадут?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Значит места их остановок совпадут через 16 800 м от пункта отправления.

Ответ: через 16 800 м.

176. В ящике лежит меньше 80 мандаринов. Известно, что их можно разделить поровну менаду двумя, тремя или пятью детьми, но нельзя разделить поровну между четырьмя детьми. Сколько мандаринов лежит в ящике?

1) Найдём наименьшее общее кратное для чисел 2, 3 и 5.

Мы знаем, что все эти числа простые. Значит:

НОК (2, 3, 5) = 2 • 3 • 5 = 6 • 5 = 30.

3) Так как кратными числам 2, 3 и 5 будут все числа, кратные 30, то в ящике могло бы также лежать и 60 мандаринов (60

Значит у данной задачи может быть единственный ответ: в ящике лежит 30 мандаринов.

Ответ: 30 мандаринов.

177. Саша ходит в бассейн один раз в три дня. Коля — раз в четыре дня, Петя — раз в пять дней. Мальчики встретились в бассейне во вторник. Через сколько дней и в какой день недели они встретятся в следующий раз?

1) Найдём наименьшее общее кратное для чисел 3, 4 и 5, а для этого разложим их на простые множители:

НОК (2, 4, 5) = 3 • 2² • 5= 15 • 4 = 60.

2) Каждая неделя содержит в себе 7 дней. Найдём, сколько целых недель и ещё дней пройдёт до новой встречи мальчиков:

Значит до новой встречи пройдёт ровно 8 недель и ещё 4 дня.

3) Ровно 7 недель после вторника закончатся в понедельник, а ещё 4 дня — это:

Значит новая встреча мальчиков произойдёт в пятницу.

Ответ: мальчики встретятся через 60 дней, встреча произойдёт в пятницу.

178. Готовя подарки к Новому году, члены родительского комитета 6 класса увидели, что имеющиеся конфеты можно разложить поровну по 15 штук или по 20 штук в один подарок. Сколько было конфет, если известно, что их было больше 600 и меньше 700?

1) Найдём наименьшее общее кратное для чисел 15 и 20.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Значит минимально возможное количество конфет — 60 шт.

2) Мы знаем, что конфет было больше 600 и меньше 700. Число 60 не входит в этот диапазон. Значит надо найти число, которое будет кратно 60 и будет удовлетворять данному условию. Перечислим числа, кратные 60:

Из всех чисел только одно число больше 600 и меньше 700. Это число 660.

Ответ: было 660 конфет.

Упражнения для повторения

179. Если к данному числу прибавить 2, то полученное число будет кратно 5. Чему равен остаток от деления данного числа на 5?

Для того, чтобы число было кратно 5, надо чтобы оно оканчивалось на цифру 0 или на цифру 5.

Значит данное число должно оканчиваться либо на 3, либо на 8. Например:

Если число данное число оканчивается на 3, то при делении его на 5 остаток будет равен 3. Например:

Если число оканчивается на 8, то при делении его на 5 остаток также будет равен 3:

Значит, какое бы заданное число, удовлетворяющее условию, мы не делили на 5, в остатке всегда будет получиться число 3.

180. Белый аист пролетел 48 км со скоростью 40 км/ч. Сколько взмахов крыльями сделал при этом аист, если каждую секунду он делает два взмаха?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

1) 48 : 40 = 1,2 (часа) — потребуется аисту для того, чтобы пролететь 48 км.

1,2 часа = 1,2 • 3 600 = 4 320 секунды.

3) 4 320 • 2 = 8 640 (шт) — взмахов сделает аист за это время.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: 8 640 взмахов.

181. Для производства 1 т бумаги необходимо использовать 6,3 м³ древесины или 1 400 кг макулатуры. Учащиеся одной школы собрали 2 100 кг макулатуры. Сколько кубических метров древесины можно сэкономить, использовав для производства бумаги собранную школьниками макулатуру?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

1) 2 100 : 1 400 = 1,5 (раза) — собрали макулатуры больше, чем требуется на 1 тонну бумаги.

2) 6,3 • 1,5 = 9,45 (м³) — древесины потребовалось бы для производства такого юе количества бумаги, как из собранной макулатуры.

3) 9,45 — 6,3 = 3,15 (м³) — можно сэкономить.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Ответ: можно сэкономить 3,15 м³ древесины.

182. Останкинская телебашня в Москве является самой высокой в Европе отдельно стоящей конструкцией. Высота Эйфелевой башни (г. Париж, Франция) вместе с антенной равна 324 м, что составляет Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10высоты Останкинской телебашни. Останкинская телебашня состоит из железобетонной основы и металлической части, которая короче железобетонной основы на 230 м. Какова высота железобетонной основы?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

1) 324 : 3 • 5 = 108 • 5 = 540 (м) — высота Останкинской телебашни в Москве.

2) Пусть х метром составляет железобетонная основа Останкинской башни. Тогда (х — 230) м — составляет металлическая конструкция. Составим уравнение:

х + (х — 230) = 540
2х — 230 = 540
2х = 770
х = 770 : 2
х = 385 (м) — составляет железобетонная основа Останкинской башни.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Готовимся к изучению новой темы

183. 1) В коробке лежит 14 шаров, из которых 5 — синего цвета. Какую

часть всех шаров составляют синие?

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10часть всех шаров составляют синие шары.

Ответ: Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10часть.

2) В коробке лежит 14 шаров, из которых Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10составляют шары красного цвета. Сколько красных шаров в коробке?

1) 14 : 7 • 3 = 2 • 3 = 6 (шт) — красные шары в коробке.

3) В коробке лежат шары, 6 из которых белого цвета. Сколько всего шаров в коробке, если белые составляют Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10всех шаров?

1) 6 : 3 • 7 = 2 • 7 = 14 (шт) — всего шаров в коробке.

184. Укажите, какие из дробей Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10:

1) правильные

Правильные дроби — это дроби, у которых числитель меньше знаменателя:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

2) неправильные

Неправильные дроби — это дроби, у которых числитель больше или равен знаменателю.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Неправильные дроби преобразуйте в смешанные числа.

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10, так как 12 : 7 = 1 (ост. 5);

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10, так как 15 : 13 = 1 (ост. 2);

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10, так как 374 : 10 = 37 (ост. 4);

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10, так как 53 : 8 = 6 (ост. 5);

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10, так как 72 : 71 = 1 (ост. 1).

185. Начертите координатный луч, взяв за единичный такой отрезок, длина которого в 6 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам:

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Можно ли утверждать что число 60 кратное числа 10. Смотреть фото Можно ли утверждать что число 60 кратное числа 10. Смотреть картинку Можно ли утверждать что число 60 кратное числа 10. Картинка про Можно ли утверждать что число 60 кратное числа 10. Фото Можно ли утверждать что число 60 кратное числа 10

Задача от мудрой совы

186. На чудо-дереве садовник вырастил 85 бананов и 70 апельсинов. Каждый день он срывает два плода, и сразу на дереве вырастает один новый. Если садовник срывает два одинаковых фрукта, то вырастает апельсин, а если два разных — то банан. Каким окажется последний фрукт на этом дереве?

Мы знаем, что изначально было нечётное количество бананов и чётное количество апельсинов. Рассмотрим разные варианты развития событий:

СорвалВырослоОсталось
1 банан + 1 апельсин1 бананбананы — столько же — нечётное число

апельсины — на 1 меньше

2 банана1 апельсинбананы — на 2 меньше — нечётное число

апельсины — на 1 больше

2 апельсина1 апельсинбананы — столько же — нечётное число

апельсины — на 1 меньше

Мы видим, что сколько бы фруктов не срывал садовник, бананов всегда остаётся нечётное число. Это значит, что последним фруктом (остался только 1) на дереве может быть только банан.

Источник

Вам также понравится

красивое фото блинчики с вареньем

admin 0

люба ким маринованные помидоры

admin 0

женский монастырь рядом с козельском

admin 0

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *