помехоустойчивое кодирование при хранении и передаче информации
8. Помехоустойчивое кодирование. Классификация помехоустойчивых кодов
Помехоустойчивое кодирование — кодирование, предназначенное для передачи данных по каналам с помехами, обеспечивающее исправление возможных ошибок передачи вследствие помех.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — помехоустойчивые коды.
Классификация помехоустойчивых кодов
В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки. Избыточные элементы размещаются в определенном порядке между информационными.
Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы информационной и проверочной частей кодовой комбинации всегда стоят на определенных местах. В неразделимых кодах деление на информационные и проверочные разряды отсутствует.
Разделимые коды, в свою очередь, делятся на систематические (линейные) и несистематические (нелинейные). Систематическими кодами называются блочные разделимые (n,k)-коды, в которых проверочные элементы представляют собой линейные комбинации информационных, несистематические коды таким свойством не обладают.
Помехоустойчивое кодирование предполагает введение в передаваемое сообщение, наряду с информационными, так называемых проверочных разрядов, формируемых в устройствах защиты от ошибок (кодерах-на передающем конце, декодерах — на приемном). Избыточность позволяет отличить разрешенную и запрещенную (искаженную за счет ошибок) комбинации при приеме, иначе одна разрешенная комбинация переходила бы в другую.
Существующие помехоустойчивые коды можно разделить на ряд групп, только часть из которых используется для обнаружения ошибок в передаваемых по сети пакетах. В группе систематических (линейных) кодов общим свойством является то, что любая разрешенная комбинация может быть получена в результате линейных операций над линейно-независимыми векторами. Это способствует упрощению аппаратной и программной реализации данных кодов, повышает скорость выполнения необходимых операций.
Рис. 1.1. Классификация помехоустойчивых кодов
Клод Шеннон сформулировал теорему для случая передачи дискретной информации по каналу связи с помехами, утверждающую, что вероятность ошибочного декодирования принимаемых сигналов может быть обеспечена сколь угодно малой путем выбора соответствующего способа кодирования сигналов. В теореме Шеннона не говорится о том, как нужно строить помехоустойчивые коды. Однако в ней указывается на принципиальную возможность кодирования, при котором может быть обеспечена сколь угодно высокая верность передачи. Это явилось стимулом к разработке помехоустойчивых кодов.
Помехоустойчивость кодирования обеспечивается за счет введения избыточности в кодовые комбинации, т.е. за счет того, что не все символы в кодовых комбинациях используются для передачи информации.
Все помехоустойчивые коды можно разделить на два основных класса: блочные и непрерывные (рекурентные или цепные).
В блочных кодах каждому сообщению (или элементу сообщения) сопоставляется кодовая комбинация (блок) из определенного количества разрядов. Блоки кодируются и декодируются отдельно друг от друга.
Блочные коды могут быть равномерными, когда длина кодовых комбинаций п постоянна, или неравномерными, когда п непостоянно.
В непрерывных кодах введение избыточности в последовательность входных символов осуществляется без разбивки ее на отдельные блоки. Процессы кодирования и декодирования в непрерывных кодах имеют также непрерывный характер.
Как блочные, так и непрерывные коды в зависимости от методов внесения избыточности подразделяются на разделимые и неразделимые. В разделимых кодах четко разграничена роль отдельных символов. Одни символы являются информационными, другие являются проверочными и служат для обнаружения и исправления ошибок. Разделимые блочные коды называются обычно п,k-кодами, где п – длина кодовых комбинаций, k – число информационных символов в комбинациях.
Неразделимые коды не имеют четкого разделения кодовой комбинации на информационные и проверочные символы.
Разделимые блочные коды делятся, в свою очередь, на несистематические и систематические. Несистематические разделимые коды строятся таким образом, что проверочные символы определяются как сумма подблоков длины l, на которые разделяется блок информационных символов.
Большинство известных разделимых кодов составляют систематические коды. У этих кодов значение проверочных символов определяется в результате проведения линейных операций над определенными информационными символами. Для случая двоичных кодов каждый проверочный символ выбирается таким, чтобы его сумма по модулю два с определенными информационными символами стала равной нулю (т.е. сумма единиц была четной). Декодирование сводится к проверке на четность определенных групп символов. В результате таких проверок дается информация о наличии ошибок, а в случае необходимости – о позиции символов, где имеются ошибки.
Помехоустойчивое кодирование с иcпользованием различных кодов
Это продолженеие статьи о помехоустойчивом кодировании, которая очень долго лежала в черновиках. В прошлой части нет ничего интересного с практической точки зрения — лишь общие сведения о том, зачем это нужно, где применяется и т.п. В данной части будут рассматриваться некоторые (самые простые) коды для обнаружения и/или исправления ошибок. Итак, поехали.
Попытался все описать как можно легче для человека, который никогда не занимался кодированием информации, и без каких-либо особых математических формул.
Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.
По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Избыточность кода — это количество проверочной информации в сообщении. Рассчитывается она по формуле:
k/(i+k), где
k — количество проверочных бит,
i — количество информационных бит.
Например, мы передаем 3 бита и к ним добавляем 1 проверочный бит — избыточность составит 1/(3+1) = 1/4 (25%).
Код с проверкой на четность
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.
Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.
Код Хэмминга
первый проверочный бит на 2 0 = 1;
второй проверочный бит на 2 1 = 2;
третий проверочный бит на 2 2 = 4;
r1 = i1 + i2 + i4
r2 = i1 + i3 + i4
r3 = i2 + i3 + i4
В принципе, работа этого алгоритма разобрана очень детально в статье Код Хэмминга. Пример работы алгоритма, так что особо подробно описывать в этой статье не вижу смысла. Вместо этого приведу структурную схему кодера: 
и декодера 
(может быть, довольно запутано, но лучше начертить не получилось)
e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:
e0 = k1 + k3 + k5 + k7 mod 2
e1 = k2 + k3 + k6 + k7 mod 2
e2 = k4 + k5 + k6 + k7 mod 2
Набор этих значений e2e1e0 есть двоичная запись позиции, где произошла ошибка при передаче данных. Декодер эти значения вычисляет, и если они все не равны 0 (то есть не получится 000), то исправляет ошибку.
Коды-произведения
В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке: 
Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке: 
Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования. Здесь к ним добавляются проверочные символы, а они, в свою очередь, заносятся в буфер по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.
При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается куда-нибудь. Условимся, что и внутренний, и внешний коды – коды Хэмминга, с тремя проверочными символами, то есть и тот, и другой могут исправить по одной ошибке в кодовом слове (количество «кубиков» на рисунке не критично — это просто схема). На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (крестики на рисунке в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена. 
Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце — две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.
Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.
Шифрование, помехоустойчивое кодирование и сжатие информации
Цель лекции: познакомиться с принципами совместного использования шифрования, помехоустойчивого кодирования и сжатия информации для комплексной защиты информации в процессе ее передачи и хранения.
Проблемы передачи информации и их комплексное решение
В процессе передачи информации от источника к потребителю на информацию воздействуют различные неблагоприятные факторы. Криптографические методы защищают информацию только от одного вида разрушающих воздействий – от предумышленного разрушения или искажения информации. Однако на практике при передаче информации от абонента к абоненту возможны случайные помехи на линиях связи, ошибки и сбои аппаратуры, частичное разрушение носителей данных и т.д. Таким образом, в реальных системах связи существует проблема защиты информации от случайных воздействий.
В связи с появлением сетей передачи данных высокой пропускной способности и развитием мультимедиа-технологий возникает проблема шифрования больших объемов информации. Если раньше основным типом шифруемых и передаваемых сообщений было текстовое сообщение, то в ХХI веке криптографическая защита все чаще применяется при передаче цифровых видео- и речевых сообщений, карт местности, для организации видеоконференций. Именно поэтому в последнее время возникает проблема шифрования огромных информационных массивов. Для интерактивных систем типа телеконференций, организации аудио- или видеосвязи, такое шифрование должно осуществляться в реальном режиме времени и по возможности быть незаметным для пользователей.
Решение указанных проблем, в том числе и защита от несанкционированного доступа, может быть достигнуто при комплексном использовании достижений теории информации.
Так, целью криптографического преобразования является, как известно, защита от несанкционированного доступа, аутентификация и защита от преднамеренных изменений. Помехоустойчивое кодирование выполняется с целью защиты информации от случайных помех при передаче и хранении. Эффективное кодирование производится с целью минимизации объема передаваемых или хранимых данных.
На практике эти три вида преобразования информации обычно используются совместно. Так, например, некоторые программные пакеты перед шифрованием архивируют обрабатываемые данные. С другой стороны, реальные системы передачи информации, будь то локальные и глобальные сети передачи данных, или компьютерные носители информации (CD или DVD-диски) всегда имеют в составе системы защиты информации средства контроля и коррекции случайных ошибок.
Для того, чтобы более эффективно использовать на практике криптографические методы защиты информации, рассмотрим основные положения теорий помехоустойчивого и эффективного кодирования, используемые в системах защиты информации.
Помехоустойчивое кодирование
Как уже отмечалось, вопросы криптографического преобразования информации тесно связаны с вопросами помехоустойчивого кодирования сообщений. Это обусловлено, с одной стороны (теоретической), тем, что и при криптографическом шифровании, и при помехоустойчивом кодировании используются одни и те же законы теории информации. С другой стороны (практической) процессы накопления, хранения и передачи информации протекают в условиях воздействия помех, способных исказить хранимые и обрабатываемые данные. Это обуславливает актуальность разработки и использования методов, позволяющих обнаруживать и корректировать подобные ошибки. С математической точки зрения задача сводится к синтезу так называемых помехоустойчивых кодов.
Аналогично понятию шифра в криптографии при обсуждении помехоустойчивого кодирования и вопросов сжатия сообщений вводят понятие кода. Вообще кодом называется совокупность знаков, а также система правил, позволяющая представлять информацию в виде набора таких знаков. Кодовым словом называют любой ряд допустимых знаков. Например, двоичное число 1100 можно считать двоичным 4-разрядным кодовым словом.
Общая идея помехоустойчивого кодирования состоит в том, что из всех возможных кодовых слов считаются допустимыми не все, а лишь некоторые из них. Например, в коде с контролем по четности считаются допустимыми лишь слова с четным числом единиц. Ошибка превращает допустимое слово в недопустимое и поэтому обнаруживается.
Помехоустойчивые коды делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды характеризуются так называемым минимальным кодовым расстоянием. Вообще, расстоянием по Хэммингу (по имени американского математика Р.У. Хэмминга) между двумя кодовыми словами называется число разрядов, в которых они различны. При этом в качестве минимального кодового расстояния выбирается наименьшее из всех расстояний по Хэммингу для любых пар различных кодовых слов, образующих код.
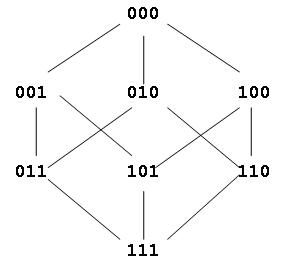
Например, пусть мы используем только трехразрядные двоичные слова. Всего таких кодовых слов может быть восемь. Те кодовые слова, которые отличаются только на одну единицу, называются соседними. Например, кодовые слова 101 и 111 – соседние, так как отличаются только средним разрядом, а слова 101 и 110 – не соседние, так как у них отличаются два последних разряда. Изобразим все трехразрядные двоичные комбинации и соединим линией соседние кодовые слова. Тогда мы получим схему, как на рис. 14.1. Минимальное кодовое расстояние между словами обычного, не помехоустойчивого кода равно единице.
В случае использования всех трехразрядных двоичных слов для передачи сообщений все они будут считаться допустимыми. Применим контроль по условию четности. Тогда допустимыми будут только выделенные рамками слова с четным числом единиц (см. рис. 14.2).
Помехоустойчивое кодирование. Коды Хэмминга
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
По используемому алфавиту:
Блочные коды делятся на
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.