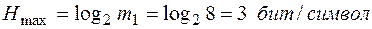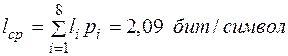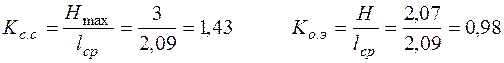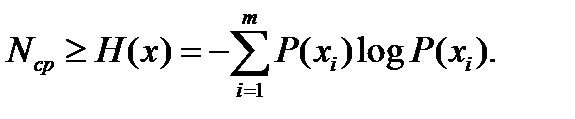понятие об оптимальном кодировании информации
Оптимальное кодирование
Кодирование
Оптимальным кодированием называется процедура преобразования символов первичного алфавита m1 в кодовые слова во вторичном алфавите m2, при котором средняя длина сообщений во вторичном алфавите имеет минимально возможную длину.
Коды, представляющие первичные алфавиты с неравномерным распределением символов, имеющие среднюю минимальную длину кодового слова во вторичном алфавите, называются оптимальными неравномерными кодами (ОНК).
Эффективность ОНК оценивают при помощи двух коэффициентов:
1. коэффициента статического сжатия

который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением методов нестатистического кодирования.
2. коэффициента относительной эффективности
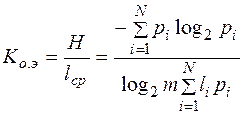
который показывает, насколько используется статическая избыточность передаваемого сообщения.
Из свойств оптимальных кодов вытекают принципы их построения:
— выбор каждого кодового слова необходимо производить так, чтобы содержащееся в нем количество информации было максимальным,
— буквам первичного алфавита, имеющим большую вероятность, присваиваются более короткие кодовые слова во вторичном алфавите.
Принципы оптимального кодирования определяют методики построения оптимальных кодов.
I. Построение ОНК по методике Шеннона-Фано для ансамбля из M сообщений сводится к следующей процедуре:
1) множество из M сообщений располагают в порядке убывания вероятностей;
2) первоначальный ансамбль кодируемых сигналов разбивают на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны;
3) первой группе присваивают символ 0, второй группе символ 1;
4) каждую из подгрупп делят на две группы так, чтобы их суммарные вероятности были по возможности равны;
Таблица 5.4 – Оптимальный код равновероятных букв
| Буква | Кодовое слово полученное после разбиения | |
| первого | второго | третьего |
| А1 А2 А3 А4 А5 А6 А7 А8 |
Проверка оптимальности кода осуществляется путем сравнения энтропии кодируемого (первичного) алфавита со средней длиной кодового слова во вторичном алфавите.
Для рассматриваемого примера энтропия источника сообщений
а среднее число двоичных знаков на букву кода
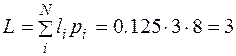
Таким образом, H = L, т. е. код является оптимальным для данного ансамбля сообщений.
Вывод: Для ансамблей равновероятных сообщений оптимальным является равномерный код. Если число исходных элементов ансамбля равно целой степени двух, то всегда H = L.
Решение проиллюстрируем в таблице 5.5.
Таблица 5.5 – Оптимальный код неравновероятных букв
| ai | pi | Кодовое слово после разбиения | Знаков | lipi | ||
| 0,5 | — | — | — | — | — | 0,5 |
| 0,25 | — | — | — | — | 0,5 | |
| 0,098 | — | — | 0,392 | |||
| 0,052 | — | — | 0,208 | |||
| 0,04 | — | — | 0,16 | |||
| 0,03 | — | 0,15 | ||||
| 0,019 | 0,114 | |||||
| 0,011 | 0,066 |
Недостатком методики Шеннона – Фано является неоднозначность построения ОНК. В методике Хаффмена этого недостатка нет.
ІІ. Хаффмен предложил следующий метод построения ОНК:
1) Символы первичного алфавита выписываются в порядке убывания вероятностей.
3) Последние символы с учетом образованного символа вновь объединяют и получают новый, вспомогательный, символ.
На практике обычно не производят многократного выписывания вероятностей символов, а обходятся элементарными геометрическими построениями, суть которых для кодов с числом качественных признаков m = 2 сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность, а затем, с учетом вероятностей вновь образованных символов, опять производят попарное объединение символов с наименьшими вероятностями и таким образом строят двоичное кодовое дерево, в вершине которого стоит символ с вероятностью 1.

Построить методом Хаффмена оптимальный код для алфавита со следующим распределением вероятностей появления букв в тексте: A = 0,5; B = 0,15; C = 0,12; D = 0,1;
Сначала находят буквы с наименьшими вероятностями 0,02 (H) и 0,03 (G), затем проводят от них линию к точке, в которой вероятность появления буквы G равна 0,05. Затем берут две наименьшие вероятности 0,04 (F) и 0,04 (E) и получают новую точку с вероятностью 0,08.
Теперь наименьшими вероятностями обладают точки, соответствующие вспомогательным символам с вероятностями 0,05 и 0,08. Соединяем их линией с новой точкой, соответствующей вспомогательному символу с вероятностью 0,13.
Продолжаем алгоритм до тех пор, пока линия от основных и вспомогательных символов не сольются в точке, дающую суммарную вероятность, равную 1.
Полученные коды представлены в таблице 5.6.
Таблица 5.6 – Двоичный код Хаффмена для восьми сообщений
| Буква | Вероятность | ОНК | Число знаков в кодовом слове | pili |
| A B C D E F G H | 0,50 0,15 0,12 0,10 0,04 0,04 0,03 0,02 | 0 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 | 0,50 0,45 0,36 0,30 0,20 0,20 0,15 0,10 |
Построить код Хаффмена для передачи сообщений при помощи трех частот f1, f2, f3, если символы первичного алфавита встречаются в сообщениях со следующими вероятностями: А = 0,24; Б = 0,18; В = 0,38;
Таблица 5.7 – Троичный код Хаффмена для семи сообщений
| Буква | Вероятность | Дерево | Код |
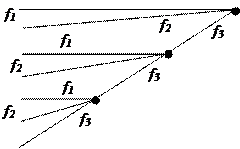 В А Б Г Д Е Ж В А Б Г Д Е Ж | 0,38 0,24 0,18 0,1 0,06 0,02 0,02 | f1 f2 f3f1 f3f2 f3f3f1 f3f3f2 f3f3f3 |
Полученный код легко декодируется, так как ни один код не начинается с f1 и f2, кроме одного одноразрядного кода.
К недостаткам алгоритма относятся:
1. Необходимость при кодировании двукратного прочтения файла первый раз для подсчета частоты вхождения символов,
второй – непостредственно для кодирования.
2. Необходимость хранения вместе с сжатым файлом декодирующего дерева для возможности восстановления файла.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Вопрос 2. Оптимальное кодирование



Введение
Измерительная информация в силу дискретности процесса измерения является дискретной. Дискретными являются различимые состояния объекта информации: дискретизированные (квантованные) значения физических величин, слова, буквы текста и т.д. Для обеспечения возможности передачи информации об этих дискретных состояниях (т.е. сообщению) каждому из них нужно поставить в соответствие некоторую синтаксическую конструкцию – кодировать сообщение. В лекции рассматриваются вопросы оптимального и помехоустойчивого кодирования.
Вопрос 1. Основные положения, термины и определения. Классификация кодов
Формально-математическое определение кодирования:
Пусть даны конечные множества Х, Y. Будем интерпретировать Х как множество исходных дискретных сообщений, Y как множество кодовых слов.
Сама операция сопоставления называемся кодированием сообщения.
Совокупность кодовых слов, обозначающих дискретные сообщения, называется кодом.
Классификация кодов
1. По наличию избыточности:
2. По значности (длине кодового слова):
3. По типу оператора кодирования:
Классификация избыточных кодов:
1. По возможностям коррекции ошибок:
2. По количеству кодируемых символов:
— непрерывные (древовидные, рекуррентные сверточные, цепные);
2. По возможности разделения информационных и проверочных символов:
Вопрос 2. Оптимальное кодирование
Поскольку кодирование есть процедура, требующая расхода ресурсов вычислительной системы, при кодировании сообщений дискретного источника возникает задача выбора правила оптимального кодирования (критерия).
Естественно полагать оптимальным такое правило кодирования (критерий), при котором:
–во-первых, кодовые слова могут быть декодированы в исходную последовательность букв источника;
–во-вторых, число кодовых букв, затрачиваемых на одну букву источника, в среднем минимально.
Очевидно, что «экономнее» будет кодер, в котором более вероятным буквам источника сопоставляются более короткие кодовые слова, т.е. в общем случае оптимальный код должен быть неравномерным.
Среднее число кодовых букв на одну букву источника можно определить по формуле
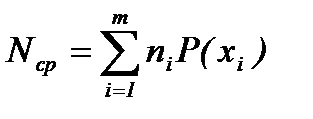
где ni – число кодовых букв, кодирующих слово xi источника,
P(xi) – вероятность появления буквы xi на выходе дискретного источника.
Нижним теоретическим пределом для Nср является энтропия Шеннона
В оптимальном коде избыточность, связанная с неравномерностью появления символов полностью исключается.
Данные коды являются оптимальными с точки зрения «экономичности», в них минимизируется избыточность, однако они применимы для передачи информации только в каналах без искажений. Искажение любого бита кода ведет к искажению закодированного слова.
Лекция № 19
Тема: Понятие об оптимальном кодировании информации
Большинство кодов, используемых при кодировании информации без учета статистических свойств источника и помех в канале связи, основано на системах счисления (двоичной, десятичной, восьмеричной, шестнадцатеричной).
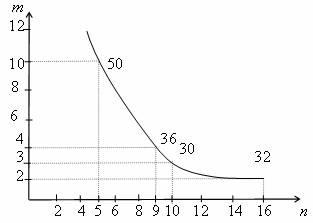
Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи. Однако с ростом основания усложняются устройства передачи и приема сигналов, так как логические элементы в этом случае должны иметь большее число устойчивых состояний. Если учитывать оба эти обстоятельства, то целесообразно выбрать систему, обеспечивающую минимум произведения основания кода т на количество разрядов n для выражения любого числа. Найдем этот минимум по графику для большого числа 6000010.
Рисунок 1. График зависимости числа разрядов п от основания кода т для числа 60000
Из графика следует, что наиболее эффективной системой является троичная. Незначительно уступают ей двоичная и четверичная. Системы с основанием десять и более значительно хуже.
С точки зрения удобства физической реализации логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе.
Действительно, арифметические операции в двоичной системе достаточно просты: сложение вычитание умножение
Сложение по модулю в двоичной системе также просто:
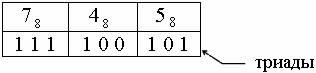
Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании (особенно для микро- и мини-ЭВМ в машинных кодах).
Чтобы сохранить преимущества двоичной системы, используют двоично-десятичные коды. В таком коде каждая цифра десятичного числа записывается в виде четырехразрядного двоичного числа. С помощью четырех разрядов можно образовать шестнадцать различных комбинаций, из которых любые десять могут составить двоично-десятичный код. Наиболее распространен код 8-4-2-1. Этот код относится к взвешенным кодам. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Он соответствует первым десяти комбинациям натурального двоичного кода (табл. 1).
| Число в десятичном Коде | Двоично-десятичный код 8-4-2-1 | Двоично-десятичный код 5-1-2-1 |
Код 8-4-2-1 обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.
Перевод чисел из десятичного в двоично-десятичный код осуществляется перфоратором в процессе переноса информации на перфоленту или перфокарту. Последующее преобразование в двоичный код осуществляется по специальной программе в самой машине. Двоично-десятичные коды с весами 5-1-2-1 и 2-4-2-1 используются при поразрядном уравновешивании в цифровых измерительных приборах (цифровые вольтметры и т.п.).
Недостатки взвешенных кодов: при передаче информации по каналам связи под действием помех отдельные элементы кода могут так исказиться, что будут приняты неверно. Например, вместо «0» будет принят элемент «1» или наоборот. Если будет искажен старший разряд, то ошибка будет значительно больше, чем при искажении младшего разряда. С этой точки зрения лучше применять невзвешенный код, у которого ошибки, вызванные помехами, были бы одинаковыми для любого разряда.
В невзвешенных кодах позициям (разрядам) кодовой комбинации не приписывают определенных весов. Вес имеет лишь вся кодовая комбинация в совокупности. Рассмотрим невзвешенный двоичный рефлексный код Грея (табл. 2).
| Десятичное число | Двоичный код вес 8-4-2-1 | Код Грея |
| . | … | … |
Правило получения кода Грея: кодовую комбинацию натурального двоичного кода складывают по модулю 2 с такой же комбинацией, сдвинутой на один разряд вправо, при этом младший разряд сдвинутой комбинации отбрасывается.
Характерные особенности кода Грея:
1) каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (в одном разряде);
2) смена значений элементов в каждом разряде (1 на 0 или 0 на 1) при переходе от комбинации к комбинации в коде Грея происходит вдвое реже, чем в натуральном двоичном коде. Это свойство кода Грея позволяет получить точность кодирования выше по сравнению с натуральным двоичным кодом при том же быстродействии схемы кодирования;
3) при сложении двух соседних комбинаций кода Грея по модулю 2 (mod2) число единиц равно числу разрядов минус три (n-3). Это свойство кода Грея можно использовать для проверки правильности принятых комбинаций.
В коде Грея можно выделить оси симметрии (оси отражения), относительно которых наблюдается идентичность элементов в некоторых разрядах. Так, например, имеет место симметрия относительно оси, проведенной между числами 7 и 8 (идентичны три символа младших разрядов). Эта особенность и послужила основанием для введения термина «рефлексный», то есть отраженный код.
Рассмотренные свойства кода Грея показывают, что он удобен для аналого-цифрового преобразования различных непрерывных сообщений и их передачи по каналам связи (сервосистемы).
Недостатком кода Грея и других рефлексных кодов является то, что эти коды невзвешенные, их трудно обрабатывать с помощью ЭВМ, так как сложнее выполнять декодирование.
Преобразование кода Грея в натуральный двоичный код выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0». (Пример: 910=1101гр =10012).
Контрольные вопросы:
1. Что такое триады?
2. Что такое тетрады?
3. Достоинства и недостатки взвещенных кодов.
Электронные средства сбора, обработки и отображения информации
Оглавление
Оптимальное кодирование
Большинство кодов, используемых при кодировании информации без учета статистических свойств источника и помех в канале связи, основано на системах счисления (двоичной, десятичной, восьмеричной, шестнадцатеричной).
Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи. Однако с ростом основания усложняются устройства передачи и приема сигналов, так как логические элементы в этом случае должны иметь большее число устойчивых состояний. Если учитывать оба эти обстоятельства, то целесообразно выбрать систему, обеспечивающую минимум произведения основания кода т на количество разрядов п для выражения любого числа. Найдем этот минимум по графику для большого числа 60000
Из графика следует, что наиболее эффективной системой является троичная. Незначительно уступают ей двоичная и четверичная. Системы с основанием десять и более значительно хуже.
С точки зрения удобства физической реализации логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе.
Действительно, арифметические операции в двоичной системе достаточно просты:
Сложение по модулю в двоичной системе также просто:
0
0
1
1
Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании (особенно для микро- и мини-ЭВМ в машинных кодах).
Чтобы сохранить преимущества двоичной системы, используют двоично-десятичные коды. В таком коде каждая цифра десятичного числа записывается в виде четырехразрядного двоичного числа. С помощью четырех разрядов можно образовать шестнадцать различных комбинаций, из которых любые десять могут составить двоично-десятичный код. Наиболее распространен код 8-4-2-1. Этот код относится к взвешенным кодам. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Он соответствует первым десяти комбинациям натурального двоичного кода (табл. 2.1).
Число в десятичном
Код 8-4-2-1 обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.
Перевод чисел из десятичного в двоично-десятичный код осуществляется перфоратором в процессе переноса информации на перфоленту или перфокарту. Последующее преобразование в двоичный код осуществляется по специальной программе в самой машине. Двоично-десятичные коды с весами 5-1-2-1 и 2-4-2-1 используются при поразрядном уравновешивании в цифровых измерительных приборах (цифровые вольтметры и т.п.).
Недостатки взвешенных кодов: при передаче информации по каналам связи под действием помех отдельные элементы кода могут так исказиться, что будут приняты неверно. Например, вместо «0» будет принят элемент «1» или наоборот. Если будет искажен старший разряд, то ошибка будет значительно больше, чем при искажении младшего разряда. С этой точки зрения лучше применять невзвешенный код, у которого ошибки, вызванные помехами, были бы одинаковыми для любого разряда.
В невзвешенных кодах позициям (разрядам) кодовой комбинации не приписывают определенных весов. Вес имеет лишь вся кодовая комбинация в совокупности. Рассмотрим невзвешенный двоичный рефлексный код Грея (табл. 2.2).
Правило получения кода Грея: кодовую комбинацию натурального двоичного кода складывают по модулю 2 с такой же комбинацией, сдвинутой на один разряд вправо, при этом младший разряд сдвинутой комбинации отбрасывается.
Характерные особенности кода Грея:
1) каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (в одном разряде);
2) смена значений элементов в каждом разряде (1 на 0 или 0 на 1) при переходе от комбинации к комбинации в коде Грея происходит вдвое реже, чем в натуральном двоичном коде. Это свойство кода Грея позволяет получить точность кодирования выше по сравнению с натуральным двоичным кодом при том же быстродействии схемы кодирования;
3) при сложении двух соседних комбинаций кода Грея по модулю 2 (mod 2) число единиц равно числу разрядов минус три (n-3). Это свойство кода Грея можно использовать для проверки правильности принятых комбинаций.
В коде Грея можно выделить оси симметрии (оси отражения), относительно которых наблюдается идентичность элементов в некоторых разрядах. Так, например, имеет место симметрия относительно оси, проведенной между числами 7 и 8 (идентичны три символа младших разрядов). Эта особенность и послужила основанием для введения термина «рефлексный», то есть отраженный код.
Рассмотренные свойства кода Грея показывают, что он удобен для аналого-цифрового преобразования различных непрерывных сообщений и их передачи по каналам связи (сервосистемы).
Недостатком кода Грея и других рефлексных кодов является то, что эти коды невзвешенные, их трудно обрабатывать с помощью ЭВМ, так как сложнее выполнять декодирование.
Преобразование кода Грея в натуральный двоичный код выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0». (Пример: