порождающая матрица линейного блокового кода применяемого для помехоустойчивого кодирования
Порождающая матрица линейного блочного кода
Итеративный код
Еще одна простая схема кодирования, которая также часто используется, может быть построена следующим образом.
| m0 | m1 | m2 | P1 = m0 +m1 +m2 |
| m3 | m4 | m5 | P2 = m3 +m4 +m5 |
| m6 | m7 | m8 | P3 = m6 + m7 + m8 |
| m0 +m3 +m6 | m1+ m4 +m7 | m2 +m5 +m8 | m0 + m0 + m1 + m1 +…. + m8 + m8 |
Таким образом, по строкам и по столбцам этой таблицы будет выполняться правило четности единиц.
Иными словами, координаты ошибки однозначно определяются номерами столбца и строки, в которых не выполняются проверки на четность. Таким образом, этот код, используя различные проверки на четность (по строкам и по столбцам), способен не только обнаруживать, но и исправлять ошибки (если известны координаты ошибки, то ее исправление состоит просто в замене символа на противоположный: если 0, то на 1, если 1 – то на 0 ).
Описанный метод кодирования, называемый итеративным, оказывается полезным в случае, когда данные естественным образом формируются в виде массивов, например, на шинах ЭВМ, в памяти, имеющей табличную структуру, и т.д. При этом размер таблицы в принципе не имеет значения (3х3 или 20х20), однако в первом случае будет исправляться одна ошибка на 3х3=9 символов, а во втором – на 20х20=400 символов.
Обратим внимание еще на один момент. Если в простом коде с проверкой на четность для обнаружения ошибки приходится добавлять к информационной последовательности всего один символ, то для того, чтобы код стал исправлять однократную ошибку, понадобилось к девяти информационным символам добавить еще семь проверочных.
Таким образом, избыточность этого кода оказалась очень большой, а исправляющая способность – сравнительно низкой. Поэтому усилия специалистов в области помехоустойчивого кодирования всегда были направлены на поиск таких кодов и методов кодирования, которые при минимальной избыточности обеспечивали бы максимальную исправляющую способность.
Простейшим способом описания, или задания, корректирующих кодов является табличный способ, при котором каждой информационной последовательности просто назначается кодовое слово из таблицы кода (табл. 3.2)
Такой способ описания кодов, кстати, применим для любых, а не только линейных кодов. Однако при больших k размер кодовой таблицы оказывается слишком большим, чтобы им пользоваться на практике (для кода с простой проверкой на четность двухбайтового слова размер таблицы составит
2 5 * 2 16 = 2000000 двоичных символов).
Другим способом задания линейных блочных кодов является использование так называемой системы проверочных уравнений, определяющих правило, по которому символы информационной последовательности преобразуются в кодовые символы. Для того же примера система проверочных уравнений будет выглядеть следующим образом:
Однако наиболее удобным и наглядным способом описания линейных блочных кодов является их задание с использованием порождающей матрицы, являющейся компактной формой представления системы проверочных уравнений:
Определение. Линейный блочный систематический (n,k)-код полностью определяется матрицей G размером k* n с двоичными матричными элементами. При этом каждое кодовое слово является линейной комбинацией строк матрицы G, а каждая линейная комбинация строк G — кодовым словом.
Тогда соответствующим ему кодовым словом U будет
С учетом структуры матрицы G символы кодового слова U будут такими:
Определенный таким образом код называется линейным блочным систематическим (n,k)-кодом с обобщенными проверками на четность, а задающая его матрица Gназывается порождающей матрицей кода.
В качестве примера рассмотрим известный (7,4)-код Хемминга, являющийся классической иллюстрацией простейших кодов с исправлением ошибок.
Пусть m = (m0, m1, m2, m3) будет тем сообщением, или информационной последовательностью, которую нужно закодировать.
Порождающая матрица G для (7. 4)-кода Хемминга имеет вид
Тогда символы соответствующего кодового слова определяются следующим образом :
| U = m× G = ( m0 m1 m2 m3 ) | = |
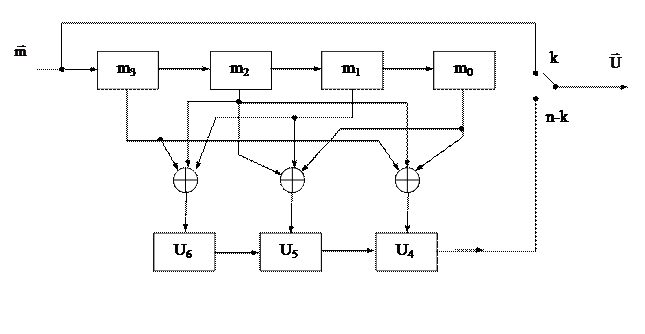
На основании порождающей матрицы G(7,4) (3.15) или приведенной системы проверочных уравнений (3.16) легко реализовать схему кодирования для рассматриваемого (7,4)-кода Хемминга (рис. 3.4).
Кодер работает точно так же, как и при простой проверке на четность, но теперь выполняет не одну общую, а несколько частичных проверок, формируя, соответственно, несколько проверочных символов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
М Вернер Основы кодирования
Глава 2. Линейные блоковые коды
2.1. Помехоустойчивое кодирование
Реальные системы передани данных не совершенны. Применяя информационную технику, мы должны учитывать возможность возникновения ошибок (вероятность ошибок) при передаче и хранении информации. Это в первую очередь относится к
• передаче данных при ограниченной мощности сигнала (спутниковая и мобильная связь)
• передаче информации но сильно зашумленным каналам (мобильная связь, высокоскоростные проводные линии связи)
• каналам связи с повышенными требованиями к надежности информации (вычислительные сети, линии передачи со сжатием данных)
Во всех вышеперечисленных случаях используются коды, контролирующие ошибки. Теория помехоустойчивого кодирования для каждого конкретного канала позволяет выбрать наиболее эффективный метод обнаружения и исправления ошибок. Существуют два взаимодополняющих метода борьбы с помехами.
• Кодирование для обнаружения ошибок приемник распознает ошибки и, в случае необходимости, производит запрос на повторную передачу ошибочного блока.
В последующих разделах идеи помехоустойчивого кодирования будут подробно объяснены на примерах линейных блоковых кодов. Здесь же мы рассмотрим простейшую модель передачи данных с использованием помехоустойчивого кодирования (рис. 2.1).
Рис. 2.1. Модель канала связи с кодированием.
Будем исходить из того, что при передаче информации используется блоковый код Хэмминга*, структура которого будет подробно раскрыта в дальнейшем. Сейчас мы ограничимся его табличным описанием. Пусть кодер источника последовательно выдает информационные слова фиксированной длины. Кодер канала заменяет каждое информационное слово u кодовым словом v в соответствии с табл. 2.1.
* Ричард В. Хэмминг: 1915/1998. американский математик.
Таблица 2.1. Кодовая таблица (7,4)-кода Хэмминга.
Декодер сравнивает принятое слово r со всеми кодовыми словами табл. 2.1. Если слово r совпадает с одним из кодовых слов, то соответствующее информационное слово и выдается потребителю. Если r отличается от всех кодовых слов, то в канале произошла обнаруживаемая ошибка.*
* Из структуры кода Хэмминга следует одно интересное свойство, которое может быть проверенно простым перебором:
Для любого произвольного вектора г существует ближайшее кодовое слово, которое или полностью совпадает с г или отличается от него только в одном двоичном разряде. Таким образом, если в векторе v при передаче по каналу произошла только одна ошибка, она всегда может быть исправлена в процессе декодирования,- Прим. перев.
Из всего вышесказанного уже можно сделать два важных вывода:
• Если в процессе передачи по зашумлснному каналу кодовое слово отобразится в другое кодовое слово, не совпадающее с переданным, то происходит необнаружимая ошибка. Назовем ее остаточной ошибкой декодирования.
• «Хорошие коды» обладают некоторой математической структурой, которая позволяет эффективно распознать, а в некоторых случаях и исправлять ошибки, возникающие при передаче информации по каналу связи.
2.2. Порождающая матрица
Важное семейство кодов образуют линейные двоичные блоковые, коды. Эти коды замечательны тем, что представляя информационные и кодовые слова в форме двоичных векторов, мы можем описать процессы кодирования и декодирования с помощью аппарата линейной алгебры, при этом, компонентами вводимых векторов и матриц являются символы 0 и 1. Операции над двоичными компонентами производятся по привычным правилам двоичной арифметики, так называемой, арифметики по модулю 2 (Табл. 2.2).
Таблица 2.2. Арифметика по модулю 2.
Вместо k бит информационного вектора в канал передается n бит кодового вектора. В этом случае говорят об избыточном кодировании со скоростью
Чем ниже скорость, тем больше избыточность кода и тем большими возможностями для защиты от ошибок он обладает (здесь, однако, надо учитывать, что с увеличением избыточности, затраты на передачу информацию также возрастают).
Таким образом, кодовое слово v и информационное слово и связаны соотношением
Например, информационный вектор и = (1010) отображается в кодовый вектор
Первое, что сразу же бросается в глаза из табл. 2.1, это совпадение последних четырех разрядов кодовых слов с информационными векторами. Такой код относится к семейству систематических кодов.
Коды, в которых информационное слово может быть непосредственно выделено из соответствующего ему кодового вектора, называются систематическими.
Порождающую матрицу любого систематического кода всегда можно путем перестановки столбцов привести к виду
Замечание. В литературе часто единичная матрица ставится на первое место. Заметим, что перестановка столбцов матрицы не оказывает никакого влияния на корректирующую способность кода.
Таким образом, в кодовом векторе систематического кода всегда можно выделить информационные и проверочные символы
Роль проверочных символов и их использование будут подробно разъяснены в следующих разделах.
2.3. Синдромное декодирование
Задача декодера заключается в том, чтобы используя структуру кода, по принятому слову г. восстановить переданный информационный вектор.
Таким образом, из первых трех столбцов порождающей матрицы G (2.2), мы получили систему трех проверочных уравнений, в которой операция производится по правилам арифметики по модулю 2 (см. табл. 2.2). Если в полученной системе уравнений хотя бы одна из компонент не равна нулю, то в канале произошла ошибка.
Запишем систему проверочных уравнений в общем виде. Для любого систематического кода с порождающей матрицей (2.5), проверочная матрица определяется как
Вектор s принято называть синдромом. Таким образом, ошибка будет обнаружена, если хотя бы одна из компонент s не равна нулю. Равенство (2.9) можно переписать в виде
Замечание. В медицине термин синдром используется для, обозначения сочетания признаков, характеризующих определенное болезненное состояние организма.
Пример: Синдромное декодирование (7, 4)-кода Хэмминга.
Используя (2.5) и (2.8), построим проверочную матрицу из порождающей матрицы кода Хэмминга (2.2). Она имеет вид
При передаче информационного слова и = (1010) по каналу без шума r = v = (0011010). Можем убедиться, что в этом случае синдром равен
Если, например, в кодовом слове произошла одиночная ошибка на четвертой позиции ( r = (0010010)), то синдромом является четвертая строка транспонированной проверочной матрицы
Таблица 2.3. Таблица синдромов однократной ошибки (7.4)-кода Хэмлинга.
Обобщим приведенные выше рассуждения, используя аппарат линейной алгебры.
Рис. 2.3. Структура кодовых векторных пространств.
Заметим, что порождающая матрица может быть разложена на матрицу Р и единичную матрицу I только в случае систематических кодов.
причем, правая часть равенства справедлива только для систематических кодов.
При синдромном кодировании приемник использует свойство ортогональности кодов
Таким образом, для каждого кодового слова v е С справедливо
Каждому принятому слову, не принадлежащему коду, соответствует отличный от нуля синдром
В рассмотренном выше примере, единичной ошибке в четвертом разряде соответствует вектор е = (0001000).
Рис. 2.4. Модель передачи информации на двоичном уровне.
В силу свойств линейности и ортогональности векторов имеем
Последнее равенство является основой синдромного декодирования. В процессе декодирования могут возникнуть следующие ситуации:
Случай 1.1: е = 0 безошибочная передача информации;
Случай 2: ошибка будет обнаружена при декодировании.
Ясно, что в первом случае, декодер всегда выдает принятое слово r потребителю, при этом существует некоторая вероятность неисправления ошибки. Во втором случае возможны два режима работы декодера.
• Распознавание ошибок. Декодер всегда определяет наличие ошибки в принятом векторе г. В зависимости от требований потребителя, принятое информационное слово или «стирается», или производится запрос на его повторную передачу.
• Коррекция ошибок. Корректирующая способность декодера может быть пояснена на примере (7,4)-кода Хэмминга, рассмотренного выше.
Декодер может выдавать потребителю ошибочное информационное слово тогда и только тогда, когда в канале произошли необнаружимые ошибки, или кратность канальной ошибки превышает корректирующую способность кода. Из рассмотренного выше примера следует, что эффективность конкретного кода зависит от области его применения и, в особенности, от канала связи. Если мы передаем информацию по каналу с аддитивным белым гауссовским шумом (АБГШ), то ошибки в кодовом слове независимы. Если при этом отношение сигнал/шум достаточно велико, то вероятность одиночной ошибки во много раз превышает вероятность ошибок высших кратностей, поэтому, использование в таком канале кода Хэмминга с исправлением однократной ошибки может оказаться весьма эффективным. С другой стороны, в каналах, где преобладают многократные ошибки (например, в каналах с замираниями), исправление одиночных ошибок лишено смысла. При практическом выборе конкретного помехоустойчивого кода необходимо также учитывать скорость его декодирования и сложность технической реализации.
Помехоустойчивое кодирование. Часть 1: код Хэмминга
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
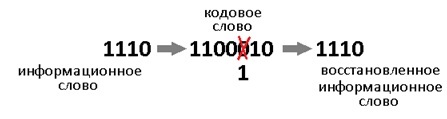
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986