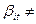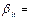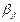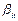префиксное и постфиксное кодирование символов
Префиксное кодирование
Кодирование с минимальной избыточностью
При равномерном кодировании общая длина кода зависит от длины сообщения. Возникает необходимость произвести неравномерное кодирование так, чтобы избыточность была минимальной.
Пусть задан алфавит А, и мы назначили неравномерные коды этому алфавиту. Например, букве А – 4 – битный код; Б – 6 – битный код; Ъ – 2 – битный код; О – 7 – битный код и так далее. Ясно, что в обычном тексте Ъ встречается реже буквы О, следовательно, если мы переназначим коды: О – 2 – битный код, Ъ – 7 – битный код, то общая длина кода уменьшится.
Алгоритм для сообщения S:
1) Находим частоту появления каждой буквы в заданном сообщении.
2) Элементарный код наименьшей длины ставим в соответствие букве с наибольшей частотой и так далее.
Замечание:
Это кодирование применимо для данного сообщения S. Для другого сообщения частота появления букв может быть другой, следовательно, элементарные коды могут быть другими.
Пусть имеется алфавит А. Таблица соответствия буквам алфавита А элементарных кодов, называется схемой кодирования.
Схема кодирования 
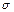


Схема кодирования называется разделимой, если любой код однозначным образом разбивается на элементарные коды, то есть если код 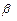
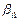

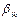
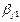
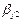
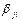
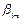
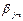

Теорема. Префиксные схемы разделимы.
Пусть схема 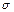

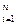
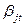



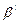
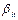

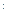
Что и требовалось доказать.
Замечание: утверждение о том, что из разделимости схемы следует её префиксносность, неверно.
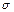


Декодирование можно начать и с конца. Если последний символ 1, то рассмотрим предпоследний. Если он 0, то эти два символа соответствуют букве b. Если он 1, то кодирование произведено неверно. В нашем случае 01 соответствует b.
Исключаем из рассмотрения эти два символа. Следующий символ от конца 0. А 0 – это а. Если у нас есть еще символы – продолжаем.
Еще пример для той же схемы:
aabbaba 
Первый символ 0. Это значит, что он может соответствовать а или являться префиксом b. Рассмотрим следующий. Если он 1, то первые два символа являются элементарным кодом b, но не а, т.к. с 1 код начинаться не может. После этого рассматриваем третий аналогично первому. Так как второй символ у нас 0, то первый символ – это элементарный код буквы а. Рассматриваем второй аналогично первому. И т.д.
Получим 0001010010 
Замечание: кодирование произведено неверно, если код начинается с 1 или две 1 стоят подряд внутри кода.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Раздел создан при поддержке компании
Кодирование
Принципиальная схема цифровой системы связи изображена на рисунке
Эта же схема подходит и для описания системы хранения информации — если заменить процесс пересылки ко каналу связи на процесс записи информации на запоминающее устройство. Будем обобщенно говорить о коммуникации, имея в виду процессы передачи, отображения и сохранения информации. Как сами средства передачи данных, так и записывающие устройства находятся под воздействиями внешних помех (природного или искусственного происхождения). Будем говорить о таких воздействиях как о шуме.
Шеннон [1] показал, что имеется принципиальная возможность использования дискретного зашумленного канала для передачи информации со сколь угодно большой степенью надежности и с любой скоростью, не превосходящей пропускную способность канала. Он также показал, что задачу надежной коммуникации можно разложить на две подзадачи:
Приведенная выше схема детализируется:
Под кодированием канала (телефонного кабеля, спутниковой антенны, оптического диска, запоминающего устройства компьютера и т.п.) понимается преобразование входной информации как набора информационных символов в другой набор символов, имеющий бóльшую длину. За счет этого увеличения длины — за счет избыточности — появляется возможность осуществления проверки информации по прохождению ею канала связи на предмет ее тождественности входной. Полученная информация должна позволять (в идеале однозначно, а на практике — с известной вероятностью ошибки) восстановить входную информацию.
Под кодированием источника (текст, изображение, звук) понимается преобразование входной информации в набор символов, более компактно (сжато) эту информацию описывающий.
Пример. Конспектирование студентом лекции можно считать кодированием лектора как источника звуковых сигналов и изображений (на доске или презентации).
Понятно, что при таком сжатии входной информации, может происходить частичная ее потеря. Проблема заключается в том, чтобы в результате процесса декодирования значительная (т.е. существенная для конкретных целей) часть входной информации была восстановлена адекватно.
Типы кодов
Блочные коды
Пример 1. Пусть алфавит языка состоит из пяти букв:
Этот пример служит примером кода, исправляющего ошибки — в данном случае одну ошибку.
декодирование всегда производить в «ближайший» кодовый блок.
Подробнее — в разделе ☞ КОД ХЭММИНГА.
Префиксные (древовидные) коды
Пример. Пусть кодирование производится по правилу:
Пример. Код
Префиксный код называется примитивным, если его невозможно сократить, т.е. если при вычеркивании любого знака хотя бы в одном кодовом слове код перестает быть префиксным.
Приведите пример непримитивного префиксного кода.
| а | б | в | г | д | е | ж | з | и | к |
|---|---|---|---|---|---|---|---|---|---|
| 00 | 01 | 1000 | 1001 | 101 | 110 | 1110 | 11110 | 111110 | 111111 |
Граф кода называется его деревом, отсюда идет другое название префиксных кодов — древовидные.
Кодирование информации
| Определение: |
| Кодирование информации (англ. information coding) — отображение данных на кодовые слова. |
Обычно в процессе кодирования информация преобразуется из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения или автоматической обработки. В более узком смысле кодированием информации называют представление информации в виде кода. Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Содержание
Код [ править ]
Виды кодов [ править ]
Все вышеперечисленные коды являются однозначно декодируемыми — для такого кода любое слово, составленное из кодовых слов, можно декодировать только единственным способом.
Примеры кодов [ править ]
Однозначно декодируемый код [ править ]
| Определение: |
| Однозначно декодируемый код (англ. uniquely decodable code) — код, в котором любое слово составленное из кодовых слов можно декодировать только единственным способом. |
Пусть есть код заданный следующей кодовой таблицей:
[math]a_1 \rightarrow b_1[/math]
[math]a_2 \rightarrow b_2[/math]
[math]a_k \rightarrow b_k[/math]
Код является однозначно декодируемым, только тогда, когда для любых строк, составленных из кодовых слов, вида:
Всегда выполняются равенства:
Заметим, что если среди кодовых слов будут одинаковые, то однозначно декодировать этот код мы уже не сможем.
Префиксный код [ править ]
| Определение: |
| Префиксный код (англ. prefix code) — код, в котором никакое кодовое слово не является префиксом какого-то другого кодового слова. |
Предпочтение префиксным кодам отдается из-за того, что они упрощают декодирование. Поскольку никакое кодовое слово не выступает в роли префикса другого, кодовое слово, с которого начинается файл, определяется однозначно, как и все последующие кодовые слова.
Пример кодирования [ править ]
Закодируем строку [math]abacaba[/math] :
Такой код можно однозначно разбить на слова:
[math]00\ 01\ 00\ 1\ 00\ 01\ 00[/math]
Преимущества префиксных кодов [ править ]
Недостатки префиксных кодов [ править ]
Пример неудачного декодирования [ править ]
Предположим, что последовательность [math]abacaba[/math] из примера передалась неверно и стала:
[math]c^<**>(abacaba) = 0001001\ 1\ 00100[/math]
Разобьем ее согласно словарю:
[math] 00\ 01\ 00\ 1\ 1\ 00\ 1\ 00[/math]
[math]a\quad b\quad a\ c\ c\quad a\ c\ a[/math]
Полученная строка совпадает только в битах, которые находились до ошибочного, поэтому декодирование неравномерного кода, содержащего ошибки, может дать абсолютно неверные результаты.
Не префиксный однозначно декодируемый код [ править ]
Как уже было сказано, префиксный код всегда однозначно декодируем. Обратное в общем случае неверно:
Мы можем ее однозначно декодировать, так как знаем, что слева от двойки и справа от тройки всегда стоит единица.
После декодирования получаем: [math]abbca[/math]
Задача №5. Кодирование в различных системах счисления, расшифровка сообщений, выбор кода.
Кодирование – это перевод информации, представленной символами первичного алфавита, в последовательность кодов.
Декодирование (операция, обратная кодированию) – перевод кодов в набор символов первичного алфавита.
Кодирование может быть равномерное и неравномерное. При равномерном кодировании каждый символ исходного алфавита заменяется кодом одинаковой длины. При неравномерном кодировании разные символы исходного алфавита могут заменяться кодами разной длины.
Код называется однозначно декодируемым, если любое сообщение, составленное из кодовых слов, можно декодировать единственным способом.
Равномерное кодирование всегда однозначно декодируемо.
Для неравномерных кодов существует следующее достаточное (но не необходимое) условие однозначного декодирования:
Сообщение однозначно декодируемо с начала, если выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова.
Сообщение однозначно декодируемо с конца, если выполняется обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова.
Кодирование в различных системах счисления
Для кодирования букв О, В, Д, П, А решили использовать двоичное представление
чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Если закодировать последовательность букв ВОДОПАД таким способом и результат записать восьмеричным кодом, то получится
Представим коды указанных букв в двоичном коде, добавив незначащий нуль для одноразрядных чисел:
Закодируем последовательность букв: ВОДОПАД — 010010001110010.
Разобьём это представление на тройки справа налево и переведём каждую тройку в восьмеричное число.
010 010 001 110 010 — 22162.
Правильный ответ указан под номером 1.
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется посимвольное кодирование: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в шестнадцатеричный вид.
Закодируем последовательность букв: ВАГБААГВ — 1101001110100110. Разобьем это представление на четвёрки справа налево и переведём каждую четверку в шестнадцатеричное число:
1101 0011 1010 01102 = D3A616
Правильный ответ указан под номером 1.
Расшифровка сообщений
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
Определите, какой набор букв закодирован двоичной строкой 1000110110110, если известно, что все буквы в последовательности – разные:
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит код можно раскодировать неоднозначно.
Значит, будем перебирать варианты, пока не получим подходящее слово :
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.
Такой вариант удовлетворяет условию, значит, окончательно получили ответ: acdeb.
Для передачи данных по каналу связи используется 5-битовый код. Сообщение содержит только буквы А, Б и В, которые кодируются следующими кодовыми словами: А — 11010, Б — 10111, В — 01101.
При передаче возможны помехи. Однако некоторые ошибки можно попытаться исправить. Любые два из этих трёх кодовых слов отличаются друг от друга не менее чем в трёх позициях. Поэтому если при передаче слова произошла ошибка не более чем в одной позиции, то можно сделать обоснованное предположение о том, какая буква передавалась. (Говорят, что «код исправляет одну ошибку».) Например, если получено кодовое слово 10110, считается, что передавалась буква Б. (Отличие от кодового слова для Б только в одной позиции, для остальных кодовых слов отличий больше.) Если принятое кодовое слово отличается от кодовых слов для букв А, Б, В более чем в одной позиции, то считается, что произошла ошибка (она обозначается ‘х’).
Получено сообщение 11000 11101 10001 11111. Декодируйте это сообщение — выберите правильный вариант.
Декодируем каждое слово сообщения. Первое слово: 11000 отличается от буквы А только одной позицией. Второе слово: 11101 отличается от буквы В только одной позицией. Третье слово: 10001 отличается от любой буквы более чем одной позицией. Четвёртое слово: 11111 отличается от буквы Б только одной позицией.
Таким образом, ответ: АВхБ.
Однозначное кодирование
Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=1, Б=01, В=001. Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Видим, что ближайший от корня дерева свободный лист (т.е. код с минимальной длиной) имеет код 000.
Для кодирования некоторой последовательности, состоящей из букв У, Ч, Е, Н, И и К, используется неравномерный двоичный префиксный код. Вот этот код: У — 000, Ч — 001, Е — 010, Н — 100, И — 011, К — 11. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему остался префиксным? Коды остальных букв меняться не должны.
Выберите правильный вариант ответа.
Примечание. Префиксный код — это код, в котором ни одно кодовое слово не является началом другого; такие коды позволяют однозначно декодировать полученную двоичную последовательность.
1) кодовое слово для буквы Е можно сократить до 01
2) кодовое слово для буквы К можно сократить до 1
3) кодовое слово для буквы Н можно сократить до 10
Для анализа соблюдения условия однозначного декодирования (условия Фано) изобразим коды в виде дерева. Тогда однозначность выполняется, если каждая буква является листом дерева:
Легко заметить, что если букву Н перенести в вершину 10, она останется листом. Т.е. кодовое слово для буквы Н можно сократить до 10.
Правильный ответ указан под номером 3.
Ты нашел то, что искал? Поделись с друзьями!
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа: