в чем состоит основной принцип помехоустойчивого кодирования
Общие принципы помехоустойчивого кодирования.
Хотя различные схемы кодирования очень непохожи друг на друга и основаны на различных математических теориях, всем им присущи два общих свойства.
Первое − использование избыточности. Закодированные последовательности всегда содержат дополнительные, или избыточные, символы.
Второе — свойство усреднения, означающее, что избыточные символы зависят от нескольких информационных символов, то есть информация, содержащаяся в кодовой последовательности X, перераспределяется также и на избыточные символы.
В дальнейшем будем называть часть помехоустойчивого кода, составленную из указанных k бит, информационной (поскольку именно они содержат информацию о передаваемом знаке первичного алфавита). Если пересылать только эти информационные биты, то любое искажение, состоящее в инверсии хотя бы одного бита, приведет к появлению новой разрешенной кодовой комбинации и, следовательно, обнаружено быть не может.
Если при передаче возникает ошибка, она проявится в том, что разрешенная кодовая комбинация перейдет в запрещенную – это можно отследить и даже исправить. Такое обнаружение, очевидно, окажется невозможным, если в результате ошибки передачи одна разрешенная кодовая комбинация перейдет в другую разрешенную. В связи с этим возникает проблема поиска таких способов избыточного кодирования, при которых вероятность перехода одной разрешенной кодовой комбинации в другую была бы минимальной.
Дата добавления: 2015-09-14 ; просмотров: 447 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
1.1. Принципы помехоустойчивого кодирования
В реальных условиях прием двоичных символов всегда происходит с ошибками, когда вместо символа «1» принимается символ «0» и наоборот. Ошибки могут возникать из-за помех, действующих в канале связи (особенно помех импульсного характера), изменения за время передачи характеристик канала (например, замирания), снижения уровня передачи, нестабильности амплитудно- и фазочастотных характеристик канала и т. п.
Общепринятым критерием оценки качества передачи в дискретных каналах является нормированная на знак или символ допустимая вероятность ошибки для данного вида сообщений. Так, допустимая вероятность ошибки при телеграфной связи может составлять 10–3 (на знак), а при передаче данных – не более 10–6 (на символ). Для обеспечения таких значений вероятностей одного улучшения только качественных показателей канала связи может оказаться недостаточным.
К первой группеотносятся методы увеличения помехоустойчивости приема единичных элементов (символов) дискретной информации, связанные с выбором уровня сигнала, отношения сигнал – помеха (энергетические характеристики), ширины полосы канала, методов приема и т. д.
Ко второй группеотносятся методы обнаружения и исправления ошибок, основанные на искусственном введении избыточности в передаваемое сообщение. Увеличить избыточность передаваемого сигнала можно различными способами. Так как объем сигнала
V = P ∆F T, (3.1)где P – мощность сигнала, Вт; ∆F – ширина спектра сигнала, Гц; T –время передачи сигнала, с, то его увеличение возможно за счет увеличения P, ∆F и T.
Практические возможности увеличения избыточности за счет мощности и ширины спектра сигнала в системах передачи дискретной информации по стандартным каналам резко ограничены. Поэтому для повышения качества приема, как правило, идут по пути увеличения времени передачи и используют следующие основные способы:
1) многократную передачу кодовых комбинаций (метод повторения);
2) одновременную передачу кодовой комбинации по нескольким параллельно работающим каналам;
3) помехоустойчивое (корректирующее) кодирование, т. е. использование кодов, исправляющих ошибки.
Наиболее целесообразно избыточность используется при применении помехоустойчивых (корректирующих) кодов.
При помехоустойчивом кодировании чаще всего считают, что избыточность источника сообщений на входе кодера равна χ = 0. Это обусловлено тем, что очень многие дискретные источники (например, цифровая информация на выходе ЭВМ) обладают малой избыт-ю.
Если избыточность первичных источников сообщений существенна, то в этих случаях по возможности стремятся ее уменьшить путем
эффективного кодирования, применяя, например коды Шеннона–Фано или Хафмена. Затем методами помехоустойчивого кодирования можно внести такую избыточностьв сигнал, которая позволит достаточно простыми средствами улучшить качество приема. Таким образом, эффективное кодирование вполне может сочетаться с помехоустойчивым.
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены к передаче, называются простыми или равнодоступными и являются полностью безызбыточными. Безызбыточные первичныекоды обладают большой»чувствительностью» к помехам.
Внесение избыточностипри использовании помехоустойчивых кодов обязательно связано с увеличением n – числа разрядов (длины) кодовой комбинации. Таким образом, все множество N = 2n комбинаций можно разбить на два подмножества: подмножество разрешенных комбинаций, т. е. обладающих определенными признаками, и подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного тем, что в канал передаются не все кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только их часть Nk, которая составляет подмножество разрешенных комбинаций.
Если при приеме выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о наличии ошибок в комбинации, т. е. таким образом решается задача обнаружения ошибок. При этом принятая комбинация не декодируется (не принимается решение о переданном сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами. Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k вкоде Хемминга добавляется r проверочных элементов для автоматического определения местоположения ошибочного символа. Коды Хеммингабудут рассмотрены подробнее далее.
1.2. Классификация помехоустойчивых корректирующих кодов
Помехоустойчивые (корректирующие) коды делятся наблочные и непрерывные.
Блочными называютсякоды, в которых информационный поток символов разбивается на отрезки и каждый из них преобразуется в определенную последовательность (блок) кодовых символов. В блочных кодах кодирование при передаче (формирование проверочных элементов) и декодирование при приеме (обнаружение и исправление ошибок) выполняются в пределах каждой кодовой комбинации (блока) в отдельности по соответствующим алгоритмам.
Непрерывные или рекуррентныекоды образуют последовательность символов, не разделяемую на отдельные кодовые комбинации. Кодирование и декодирование непрерывно совершаются над последовательностью элементов без деления их на блоки. Формирование проверочных символов ведется по рекуррентным (возвратным) правилам, поэтому непрерывные коды часто называют рекуррентными или цепными.В простейшем цепном коде каждый проверочный элемент формируется путем сложения по модулю 2 соседних или отстоящих друг от друга на определенное число позиций информационных элементов. В канал связи передается последовательность импульсов, в которой за каждым информационным следует проверочный. Подобную чередующуюся последовательность разрядов имеет,например корреляционный манчестерский код[ 3].
К непрерывным кодам относятся и сверточные коды, в которых каждый информационный символ, поступающий на вход кодирующего устройства, вызывает появление на его выходе ряда проверочных элементов, образованных суммированием по модулю 2 данного символа и k–1 предыдущих информационных символов. Рекуррентные коды позволяют исправлять групповые ошибки («пачки») в каналах связи.
Блочные коды делятся на равномерные и неравномерные. В равномерных кодах, в отличие от неравномерных, все кодовые комбинации содержат одинаковое число n-символов (разрядов) с постоянной длительностью τ0 импульсов символов кода. Равномерные коды в основном и применяются в системах связи, так как это упрощает технику передачи и приема.
Классическими примерами неравномерного кода являются код Морзе, широко применяемый в телеграфии, и код Хафмена, применяемый для компрессии информации (факсимильная связь, ЭВМ).
В этом смысле код Морзе не относится к классу корректирующих кодов.
Почти все блочные корректирующие коды принадлежат к разделимым кодам, в которых кодовые комбинации состоят из двух частей: информационной и проверочной. Их символы всегда занимают одни и те же позиции, т. е. располагаются на определенных местах. Как правило, в таких кодах, все кодовые комбинации которых содержат n символов, первые k символов являются информационными, а за ними располагаются (n–k)-проверочных символов. В соответствии с этим разделимые коды получили условное обозначение –(n, k)-коды.
В неразделимых кодахделение на информационные и проверочные символы отсутствует. К таким кодам относятся, в частности, коды с постоянным весом, так называемые равновесные коды.
Систематические кодыобразуют наиболее обширную группу (n,k)-разделимых кодов. Особенностью этих кодов является то, что проверочные (корректирующие) символы образуются с помощью линейных операций над информационными. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейной операции над набором k линейно независимых кодовых комбинаций.
Наиболее известны среди систематических кодов коды Хемминга, которые исторически были найдены раньше многих других кодов и сыграли большую роль в развитии теории корректирующих кодов. В этих кодах используется принцип проверки на четность определенного ряда информационных символов. Проверочная группа из r символов формируется поэлементно по соответствующему алгоритму. Коды Хемминга, имеющие dmin = 3, позволяют исправить одну ошибку.
Расширенные коды Хемминга строятся в результате дополнения кодов с dmin = 3 общей проверкой каждой из кодовых комбинаций на четность, т. е. еще одним проверочным символом. Это позволяет увеличить минимальное кодовое расстояние до dmin = 4.
Относительной избыточностью корректирующего кода называют величину отн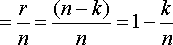
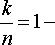
Помехоустойчивое кодирование с иcпользованием различных кодов
Это продолженеие статьи о помехоустойчивом кодировании, которая очень долго лежала в черновиках. В прошлой части нет ничего интересного с практической точки зрения — лишь общие сведения о том, зачем это нужно, где применяется и т.п. В данной части будут рассматриваться некоторые (самые простые) коды для обнаружения и/или исправления ошибок. Итак, поехали.
Попытался все описать как можно легче для человека, который никогда не занимался кодированием информации, и без каких-либо особых математических формул.
Когда мы передаем сообщение от источника к приемнику, при передаче данных может произойти ошибка (помехи, неисправность оборудования и пр.). Чтобы обнаружить и исправить ошибку, применяют помехоустойчивое кодирование, т.е. кодируют сообщение таким образом, чтобы принимающая сторона знала, произошла ошибка или нет, и при могла исправить ошибки в случае их возникновения.
По сути, кодирование — это добавление к исходной информации дополнительной, проверочной, информации. Для кодирования на передающей стороне используются кодер, а на принимающей стороне — используют декодер для получения исходного сообщения.
Избыточность кода — это количество проверочной информации в сообщении. Рассчитывается она по формуле:
k/(i+k), где
k — количество проверочных бит,
i — количество информационных бит.
Например, мы передаем 3 бита и к ним добавляем 1 проверочный бит — избыточность составит 1/(3+1) = 1/4 (25%).
Код с проверкой на четность
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка.
Начальные данные: 1111
Данные после кодирования: 11110 ( 1 + 1 + 1 + 1 = 0 (mod 2) )
Принятые данные: 10010 (изменились 2 и 3 биты)
В принятых данных число единиц четно, и, следовательно, декодер не обнаружит ошибку.
Так как около 90% всех нерегулярных ошибок происходит именно с одиночным разрядом, проверки четности бывает достаточно для большинства ситуаций.
Код Хэмминга
первый проверочный бит на 2 0 = 1;
второй проверочный бит на 2 1 = 2;
третий проверочный бит на 2 2 = 4;
r1 = i1 + i2 + i4
r2 = i1 + i3 + i4
r3 = i2 + i3 + i4
В принципе, работа этого алгоритма разобрана очень детально в статье Код Хэмминга. Пример работы алгоритма, так что особо подробно описывать в этой статье не вижу смысла. Вместо этого приведу структурную схему кодера: 
и декодера 
(может быть, довольно запутано, но лучше начертить не получилось)
e0,e1,e2 опрделяются как функции, зависящие от принятых декодером бит k1 — k7:
e0 = k1 + k3 + k5 + k7 mod 2
e1 = k2 + k3 + k6 + k7 mod 2
e2 = k4 + k5 + k6 + k7 mod 2
Набор этих значений e2e1e0 есть двоичная запись позиции, где произошла ошибка при передаче данных. Декодер эти значения вычисляет, и если они все не равны 0 (то есть не получится 000), то исправляет ошибку.
Коды-произведения
В канале связи кроме одиночных ошибок, вызванных шумами, часто встречаются пакетные ошибки, вызванные импульсными помехами, замираниями или выпадениями (при цифровой видеозаписи). При этом пораженными оказываются сотни, а то и тысячи бит информации подряд. Ясно, что ни один помехоустойчивый код не сможет справиться с такой ошибкой. Для возможности борьбы с такими ошибками используются коды-произведения. Принцип действия такого кода изображён на рисунке: 
Передаваемая информация кодируется дважды: во внешнем и внутреннем кодерах. Между ними устанавливается буфер, работа которого показана на рисунке: 
Информационные слова проходят через первый помехоустойчивый кодер, называемый внешним, т.к. он и соответствующий ему декодер находятся по краям системы помехоустойчивого кодирования. Здесь к ним добавляются проверочные символы, а они, в свою очередь, заносятся в буфер по столбцам, а выводятся построчно. Этот процесс называется перемешиванием или перемежением.
При выводе строк из буфера к ним добавляются проверочные символы внутреннего кода. В таком порядке информация передается по каналу связи или записывается куда-нибудь. Условимся, что и внутренний, и внешний коды – коды Хэмминга, с тремя проверочными символами, то есть и тот, и другой могут исправить по одной ошибке в кодовом слове (количество «кубиков» на рисунке не критично — это просто схема). На приемном конце расположен точно такой же массив памяти (буфер), в который информация заносится построчно, а выводится по столбцам. При возникновении пакетной ошибки (крестики на рисунке в третьей и четвертой строках), она малыми порциями распределяется в кодовых словах внешнего кода и может быть исправлена. 
Назначение внешнего кода понятно – исправление пакетных ошибок. Зачем же нужен внутренний код? На рисунке, кроме пакетной, показана одиночная ошибка (четвертый столбец, верхняя строка). В кодовом слове, расположенном в четвертом столбце — две ошибки, и они не могут быть исправлены, т.к. внешний код рассчитан на исправление одной ошибки. Для выхода из этой ситуации как раз и нужен внутренний код, который исправит эту одиночную ошибку. Принимаемые данные сначала проходят внутренний декодер, где исправляются одиночные ошибки, затем записываются в буфер построчно, выводятся по столбцам и подаются на внешний декодер, где происходит исправление пакетной ошибки.
Использование кодов-произведений многократно увеличивает мощность помехоустойчивого кода при добавлении незначительной избыточности.
Шифрование, помехоустойчивое кодирование и сжатие информации
Цель лекции: познакомиться с принципами совместного использования шифрования, помехоустойчивого кодирования и сжатия информации для комплексной защиты информации в процессе ее передачи и хранения.
Проблемы передачи информации и их комплексное решение
В процессе передачи информации от источника к потребителю на информацию воздействуют различные неблагоприятные факторы. Криптографические методы защищают информацию только от одного вида разрушающих воздействий – от предумышленного разрушения или искажения информации. Однако на практике при передаче информации от абонента к абоненту возможны случайные помехи на линиях связи, ошибки и сбои аппаратуры, частичное разрушение носителей данных и т.д. Таким образом, в реальных системах связи существует проблема защиты информации от случайных воздействий.
В связи с появлением сетей передачи данных высокой пропускной способности и развитием мультимедиа-технологий возникает проблема шифрования больших объемов информации. Если раньше основным типом шифруемых и передаваемых сообщений было текстовое сообщение, то в ХХI веке криптографическая защита все чаще применяется при передаче цифровых видео- и речевых сообщений, карт местности, для организации видеоконференций. Именно поэтому в последнее время возникает проблема шифрования огромных информационных массивов. Для интерактивных систем типа телеконференций, организации аудио- или видеосвязи, такое шифрование должно осуществляться в реальном режиме времени и по возможности быть незаметным для пользователей.
Решение указанных проблем, в том числе и защита от несанкционированного доступа, может быть достигнуто при комплексном использовании достижений теории информации.
Так, целью криптографического преобразования является, как известно, защита от несанкционированного доступа, аутентификация и защита от преднамеренных изменений. Помехоустойчивое кодирование выполняется с целью защиты информации от случайных помех при передаче и хранении. Эффективное кодирование производится с целью минимизации объема передаваемых или хранимых данных.
На практике эти три вида преобразования информации обычно используются совместно. Так, например, некоторые программные пакеты перед шифрованием архивируют обрабатываемые данные. С другой стороны, реальные системы передачи информации, будь то локальные и глобальные сети передачи данных, или компьютерные носители информации (CD или DVD-диски) всегда имеют в составе системы защиты информации средства контроля и коррекции случайных ошибок.
Для того, чтобы более эффективно использовать на практике криптографические методы защиты информации, рассмотрим основные положения теорий помехоустойчивого и эффективного кодирования, используемые в системах защиты информации.
Помехоустойчивое кодирование
Как уже отмечалось, вопросы криптографического преобразования информации тесно связаны с вопросами помехоустойчивого кодирования сообщений. Это обусловлено, с одной стороны (теоретической), тем, что и при криптографическом шифровании, и при помехоустойчивом кодировании используются одни и те же законы теории информации. С другой стороны (практической) процессы накопления, хранения и передачи информации протекают в условиях воздействия помех, способных исказить хранимые и обрабатываемые данные. Это обуславливает актуальность разработки и использования методов, позволяющих обнаруживать и корректировать подобные ошибки. С математической точки зрения задача сводится к синтезу так называемых помехоустойчивых кодов.
Аналогично понятию шифра в криптографии при обсуждении помехоустойчивого кодирования и вопросов сжатия сообщений вводят понятие кода. Вообще кодом называется совокупность знаков, а также система правил, позволяющая представлять информацию в виде набора таких знаков. Кодовым словом называют любой ряд допустимых знаков. Например, двоичное число 1100 можно считать двоичным 4-разрядным кодовым словом.
Общая идея помехоустойчивого кодирования состоит в том, что из всех возможных кодовых слов считаются допустимыми не все, а лишь некоторые из них. Например, в коде с контролем по четности считаются допустимыми лишь слова с четным числом единиц. Ошибка превращает допустимое слово в недопустимое и поэтому обнаруживается.
Помехоустойчивые коды делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды характеризуются так называемым минимальным кодовым расстоянием. Вообще, расстоянием по Хэммингу (по имени американского математика Р.У. Хэмминга) между двумя кодовыми словами называется число разрядов, в которых они различны. При этом в качестве минимального кодового расстояния выбирается наименьшее из всех расстояний по Хэммингу для любых пар различных кодовых слов, образующих код.
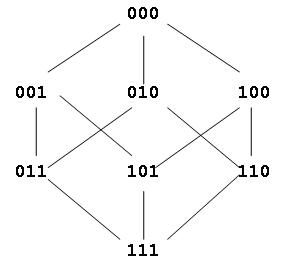
Например, пусть мы используем только трехразрядные двоичные слова. Всего таких кодовых слов может быть восемь. Те кодовые слова, которые отличаются только на одну единицу, называются соседними. Например, кодовые слова 101 и 111 – соседние, так как отличаются только средним разрядом, а слова 101 и 110 – не соседние, так как у них отличаются два последних разряда. Изобразим все трехразрядные двоичные комбинации и соединим линией соседние кодовые слова. Тогда мы получим схему, как на рис. 14.1. Минимальное кодовое расстояние между словами обычного, не помехоустойчивого кода равно единице.
В случае использования всех трехразрядных двоичных слов для передачи сообщений все они будут считаться допустимыми. Применим контроль по условию четности. Тогда допустимыми будут только выделенные рамками слова с четным числом единиц (см. рис. 14.2).
Национальная библиотека им. Н. Э. Баумана
Bauman National Library
Персональные инструменты
Помехоустойчивое кодирование и декодирование в дискретных КПС
Содержание
Базовые понятия помехоустойчивого кодирования и декодирования
Кодированием и декодированием (в широком смысле) называют любое преобразование сообщения в сигнал и обратно, сигнала в сообщение, путем установления взаимного соответствия. Преобразование следует считать оптимальным, если в конечном итоге производительность источника и пропускная способность канала окажутся равными, т.е. возможности канала будут полностью использованы. Данное преобразование разбивается на два этапа:
В свою очередь, кодирование-декодирование делится на два противоположных по своим действиям действиям этапа:
Примером экономного кодирования является передача речевого сигнала по цифровым каналам. Если ориентироваться только на смысловое (семантическое) содержание, то можно перейти к передаче текста со скоростью 5. 10 букв в секунду. С учетом объема алфавита в двоичном канале это потребует скорость передачи 25. 50 бит/с. Если устранить избыточность, связанную с неодинаковой вероятностью появления букв и их корреляцией в тексте, то, как показывают расчеты, скорость передачи может быть уменьшена до 10 бит/с. Если передавать речь в цифровой форме, используя аналого-цифровое преобразование, ориентируясь только на ширину спектра и динамический диапазон, то скорость потока двоичных символов составит 32. 64 кбит/с. Такая избыточность привела к необходимости разработки специальных кодеков речевых сигналов, называемых вокодерами, которые нашли применение при передаче речи в цифровой форме по радиоканалам. Например, в сотовых системах мобильной связи стандарта GSM скорость передачи составляет 8,5 кбит/с, причем сохраняются не только семантическое содержание, но и индивидуальные особенности говорящего. Подобные кодеки находят применение и при передаче подвижных и неподвижных изображений в цифровых телевизионных каналах.
Принцип построения помехоустойчивых кодов
Основные параметры помехоустойчивых кодов
Если код примитивный, то ошибка возникает, когда хотя бы в одном символе при приеме произошла ошибка. Вероятность такого события равна:
Для избыточного кода ошибка в приеме кодовой комбинации будет иметь место тогда, когда число ошибок превысит исправляющую способность кода tи и ее вероятность:
Различие в Рош.п и Рош.и определяется уменьшением длительности посылки при передаче избыточным кодом в n/k раз. Величины Рош.п и Рош.и могут быть найдены, если известен вид модуляции и демодуляции, отношение P0 / N0 и длительность посылок источника.
Оценочные соотношения для параметров помехоустойчивых кодов
Задача построения кода с заданной корректирующей способностью сводится к обеспечению необходимого кодового расстояния при введении избыточности. При этом желательно, чтобы число используемых проверочных символов было минимальным. Задача определения минимального числа проверочных символов, необходимых для обеспечения заданного кодового расстояния, не решена. Имеется лишь ряд оценок для максимального кодового расстояния при фиксированных n / k, которые часто используются для выяснения того, насколько построенный код близок к оптимальному. Можно показать, что если существует блочный линейный код (n, k), то для него справедливо неравенство:
Выражение (1) называется верхней границей Хэмминга. Граница Хэмминга (1) близка к оптимальной для кодов с большими значениями n / k. Для кодов с малыми значениями n / k более точной вляется верхняя граница Плоткина:
называемое нижней границей Варшамова—Гильберта. Таким образом, границы Хэмминга и Плоткина являются необходимыми условиями существования кода, а граница Варшамова—Гильберта — достаточным. Эти границы позволяют оценить эффективность блочных кодов и целесообразность их применения.
Линейное блочное кодирование
Способы задания линейных кодов
В теории кодирования матрица G называется порождающей. Тогда процесс кодирования заключается в выполнении операции:
В противном случае S не равно 0, причем вид синдрома зависит только от вектора ошибок е. Действительно:
Строение декодера линейного кода
Декодер линейного кода (рис. 1) состоит из k-разрядного сдвигающего регистра, (n — k) блоков сумматоров по модулю 2, схемы сравнения, анализатора ошибок и корректора. Регистр служит для запоминания информационных символов принятой кодовой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретному виду синдрома, получаемого в результате сравнения формируемых на приемной стороне и принятых проверочных символов, определяет места ошибочных символов. Исправление информационных символов проводится в корректоре.
Циклические коды
Циклические коды относятся к классу линейных. Поэтому для их построения достаточно знать порождающую матрицу. Несмотря на это, можно указать другой, более простой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленами b(х) вида:
Поскольку операции суммирования и вычитания по модулю 2 совпадают, то выражение (9) перепишем в виде:
Устройство кодеров циклического кода
Коды Хэмминга
Коды БЧХ
Схема декодера (рис. 6) состоит из сдвигающего регистра, сумматоров по модулю 2 и мажоритарного элемента М. Простота ее обусловлена тем, что в данном случае каждый символ кодовой комбинации участвует в одном проверочном соотношении. Код, для которого выполняется это условие, называется кодом с разделенными проверками.
Мажоритарное декодирование возможно и тогда, когда один и тот же символ участвует в нескольких проверочных соотношениях. Однако алгоритм декодирования усложняется.
Итеративные коды
Легко показать, что кодовое расстояние этого кода равно 4. Код исправляет все однократные ошибки. Их координаты определяются по номерам строк и столбцов, в которых не выполняется проверка на четность. Одновременно код обнаруживает все двукратные ошибки. Итеративные коды характеризуются большой длиной, большим кодовым расстоянием и сравнительно простой процедурой декодирования. Недостатком их является малая скорость при заданной исправляющей способности.
Каскадные коды
Каскадные коды получаются комбинированием двух или более кодов и в некоторой степени похожи на итеративные. Кодирование осуществляется следующим образом.
Декодирование двумя отдельными декодерами позволяет существенно снизить сложность по сравнению с той, которая потребуется для получения той же вероятности ошибки при одном уровне кодирования.
Каскадные коды, как и итеративные, имеют большую длину и большое кодовое расстояние. Во многих случаях они являются наилучшими среди блочных кодов. В частности, для двоичного симметричного канала при любой скорости передачи, не превосходящей пропускной способности канала, существует каскадный код, при котором вероятность ошибки может быть сколь угодно мала.
Непрерывные сверточные коды
Основные параметры сверточных кодов
Устройство кодера сверточного кода
Виды и способы задания сверточных кодов
Указанное свойство прозрачных кодов особенно важно для СПИ, использующих противоположные фазоманипулированные (ФМ) сигналы, которым свойственно явление обратной работы. Для непрозрачного кода неопределенность знака последовательности символов приходится устранять до сверточного декодирования, что приводит к увеличению вероятности ошибок. Нетрудно показать, что сверточный код будет прозрачным, если каждый его порождающий многочлен содержит нечетное число членов. Помимо рассмотренного способа задания сверточного кода, возможны и другие. В частности, выходные символы можно рассматривать как свертку импульсной характеристики кодера с информационной последовательностью (отсюда и происходит название кода). Для пояснения процессов кодирования и декодирования часто используют решетчатую диаграмму, представляющую собой одно из возможных изображений кодового дерева. Такая диаграмма для кодера на рис. 10 состоит из узлов и ветвей (ребер). Число ветвей, исходящих из узла, равно основанию кода. Число узлов равно ( 2 K − 1 <\displaystyle 2^
Методы декодирования сверточных кодов
Декодирование с вычислением проверочной последовательности
Декодирование с вычислением проверочной последовательности применяется только для систематических кодов. Оно ничем не отличается от соответствующего метода декодирования блочных кодов. На приемной стороне из принятых информационных символов формируют проверочные символы по тому закону, что и на передающей стороне, которые затем сравнивают с принимаемыми проверочными символами. В результате сравнения образуется проверочная последовательность, которая при отсутствии ошибок состоит из одних нулей. При наличии ошибок на определенных позициях последовательности появляются единичные символы. Закон формирования проверочных символов выбирается таким образом, чтобы по структуре проверочной последовательности можно было определить искаженные символы.
Декодирование по принципу максимума правдоподобия
Алгоритм Витерби
Алгоритм Витерби обладает рядом преимуществ. При небольших значениях длины кодового ограничения декодирующее устройство оказывается достаточно простым, реализуя, в то же время, высокую помехоустойчивость. Так, исследования показывают, что применение сверточных кодов с К= 3, 5 и 7 при фиксированной вероятности ошибки Pош = 10 − 5 <\displaystyle =10^<-5>\,\!> позволяет получить энергетический выигрыш 4. 6 дБ по сравнению с системой, использующей ФМ-сигналы без кодирования. Важным преимуществом по сравнению с методом последовательного декодирования является фиксация числа вычислительных операций на один декодированный символ. Декодирование по методу Витерби особенно перспективно в каналах с независимыми ошибками.
Устройство декодера Витерби
Декодер Витерби (рис. 12) состоит из синхронизатора, устройства управления и тактирования, устройства для вычисления метрик ветвей, устройства для обновления и хранения метрик ветвей, устройства для обновления и хранения гипотетических информационных последовательностей и решающего устройства. Устройство хранения и обновления метрик путей осуществляет сложение метрик ветвей с хранящимися метриками путей, проделывает необходимые сравнения и запоминает новые метрики путей. Устройство хранения и обновления гипотетических информационных последовательностей может быть выполнено на сдвигающих регистрах, в каждом из которых хранится полная информационная последовательность символов, соответствующая одному из «выживших» путей. Их число равно числу узлов. После обработки новой ветви регистры обмениваются содержимым в соответствии с тем, какие последовательности «выживают» при сравнении. В последнюю ячейку каждого регистра поступает новый информационный символ, а самый старый символ каждого регистра поступает в выходное решающее устройство. Выходное решающее устройство принимает решение о переданных информационных символах. Наилучшие результаты получаются, когда в качестве переданного информационного символа берется наиболее старый символ в последовательности с наименьшей метрикой. Иногда используют мажоритарный принцип: за переданный информационный символ берут чаще всего встречающийся символ из самых старых символов всех последовательностей. Устройство управления и тактирования задает необходимый ритм работы декодера.
Применение кодов в технических системах
Системы с обратной связью
Во многих системах, кроме основного (прямого) канала, с помощью которого сообщение передается от источника к потребителю, имеется обратный канал для вспомогательных сообщений, которые позволяют улучшить качество передачи сообщений по прямому каналу. Наиболее распространены системы с обратной связью, в которых для обнаружения ошибок применяют избыточные коды. Такие системы называются системами с решающей обратной связью, или системами с переспросом. В качестве кодов часто используют коды с проверкой на четность, простейшие итеративные коды, циклические коды и др. Они позволяют хорошо обнаруживать ошибки при сравнительно небольшой избыточности и простой аппаратурной реализации. Передаваемое сообщение кодируется избыточным кодом. Полученная комбинация передается потребителю и одновременно запоминается в накопителе-повторителе. Принятая последовательность символов декодируется с обнаружением ошибок. Если при этом ошибки не обнаружены, то сообщение поступает потребителю. В противном случае сообщение бракуется и по обратному каналу передается специальный сигнал переспроса. По этому сигналу проводится повторная передача забракованной кодовой комбинации, которая извлекается из накопителя-повторителя. Можно показать, что если в обратном канале ошибки отсутствуют, то остаточная вероятность ошибочного приема кодовой комбинации имеет вид:
Вероятности Рно и Ро.ош можно найти, если известны свойства канала и задан код. Эквивалентная вероятность ошибки имеет вид:
Среднее число передач одного сообщения определяется следующим образом:
Несмотря на то, что обратный канал можно сделать весьма помехоустойчивым (обычно скорость передачи информации в обратном канале значительно меньше, чем в прямом), тем не менее, существует конечная вероятность того, что сигнал переспроса будет принят как сигнал подтверждения, и наоборот. В первом случае сообщение не поступает потребителю, а во втором случае оно поступает дважды. Одним из средств борьбы с ошибками в обратном канале, приводящими к потере сообщения, является использование несимметричного правила декодирования, при котором вероятность ошибочного приема сигнала переспроса существенно меньше вероятности ошибочного приема сигнала подтверждения. Например, сигнал переспроса передается кодовой комбинацией из п единичных символов, а сигнал подтверждения — комбинацией из n нулей. При приеме кодовой комбинации, содержащей хотя бы одну единицу, решение принимается в пользу сигнала переспроса. Очевидно, что в этом случае вероятность ошибочного приема сигнала переспроса можно получит сколь угодно малой. Для того чтобы к потребителю не поступали лишние сообщения, обусловленные ошибочным приемом сигналов подтверждения, передаваемые кодовые комбинации либо снабжаются номерами, либо дополняются опознавательными символами, по которым можно узнать, передается кодовая комбинация в первый раз или она повторяется. При этом принятая повторная комбинация при отсутствии сигнала переспроса стирается и не поступает потребителю. Возможны и другие способы борьбы с ошибками такого рода. Системы с решающей обратной связью весьма эффективны в случае каналов с замираниями. При ухудшении состояния канала увеличивается частота переспроса (уменьшается скорость передачи информации), но вероятность ошибочных сообщений, поступающих потребителю, практически не увеличивается. При улучшении состояния канала частота переспроса уменьшается. Таким образом, система как бы автоматически приспосабливается к состоянию канала связи, используя все его возможности в отношении передачи информации. Следует заметить, что применение решающей обратной связи, конечно, не увеличивает пропускной способности прямого канала, но позволяет более простыми средствами по сравнению с длинными кодами приблизить скорость передачи информации к пропускной способности канала.
Сигнально-кодовые конструкции
Как известно, многопозиционные сигналы, такие как сигналы многократной фазовой модуляции (ФМ) и сигналы амплитудно-фазовой модуляции (АФМ), обеспечивают высокую удельную скорость передачи информации (высокую частотную эффективность) при уменьшении энергетической эффективности, а помехоустойчивые коды позволяют повышать энергетическую эффективность при снижении удельной скорости передачи. Сочетание методов многопозиционной модуляции и помехоустойчивого кодирования дает возможность повысить либо энергетическую эффективность без уменьшения частотной, либо частотную эффективность без снижения энергетической, а в ряде случаев — оба параметра. Задача заключается в формировании таких сигнальных последовательностей, которые можно достаточно плотно разместить в многомерном пространстве (для обеспечения высокой частотной эффективности) и в то же время разнести на достаточно большие расстояния (для обеспечения высокой энергетической эффективности). Такие последовательности, построенные на базе помехоустойчивых кодов и многопозиционных сигналов с плотной упаковкой, называются сигнально-кодовыми конструкциями. В качестве помехоустойчивого кода обычно используются каскадные, итеративные и сверточные коды, а в качестве многопозиционных сигналов — сигналы многократной ФМ и сигналы АФМ. Для согласования кодека двоичного помехоустойчивого кода и модема многопозиционных сигналов используется манипуляционный код, при котором большему расстоянию по Хэммингу между кодовыми комбинациями соответствует большее расстояние между соответствующими им сигналами. Этому требованию частично удовлетворяет код Грея. Возможны и другие способы такого преобразования. На рис. 13 показана структурная схема одной из возможных систем с многоуровневой ФМ и помехоустойчивым кодированием. Сформированные на выходе помехоустойчивого кодера комбинации преобразуются в кодере Грея в последовательность кодовых комбинаций длины m, которые и определяют начальную фазу радиоимпульса фиксированной длительности на выходе фазового модулятора. На приемной стороне принятый сигнал сначала синхронно детектируется фазовым модулятором. Полученная при этом последовательность символов преобразуется декодерами Грея и помехоустойчивого кода в сообщение. Применение сигнально-кодовых конструкций позволяет существенно приблизиться к границе эффективности, определяемой пропускной способностью канала.
Методы приема сигналов
Прием «в целом»
До сих пор предполагалось, что кодовые комбинации принимаются посимвольно, т. е. на приемной стороне вначале выносится решение о каждом символе кодовой комбинации, а затем по совокупности n принятых символов принимается решение о том, какая кодовая комбинация была передана. При избыточных кодах такая двухэтапная процедура принятия решения оказывается неоптимальной. Объясняется это тем, что процесс демодуляции является необратимой операцией и может сопровождаться потерей информации. Действительно, после принятия решения о символе ни соответствующий элемент сигнала, ни фактическое значение результата обработки этого символа (значение апостериорной вероятности или функции правдоподобия) в дальнейшем процессе приема (при декодировании) не принимаются во внимание. В то же время их учет мог бы привести к уменьшению вероятности ошибочного декодирования кодовой комбинации. Вся информация, содержащаяся в принимаемом сигнале, будет наиболее полно использована, если отказаться от посимвольного приема и демодулировать кодовую комбинацию в целом. Можно показать, что при использовании кода с избыточностью помехоустойчивость приема «в целом» выше помехоустойчивости поэлементного приема с исправлением ошибок, однако уступает помехоустойчивости поэлементного приема с обнаружением ошибок и переспросом по обратному каналу. При использовании кода без избыточности «прием в целом» не имеет преимуществ по сравнению с поэлементным приемом. В общем случае вычислить вероятность ошибочного приема кодовой комбинации трудно. Однако иногда, например при использовании ортогональных, биортогональных и симплексных кодов, эту вероятность можно выразить через интегралы, которые можно определить численными методами. Недостатком «приема в целом» является то, что он требует значительно более сложной аппаратуры по сравнению с поэлементным приемом. В частности, для его реализации требуется 2 k <\displaystyle 2^