в гостях у бабушки надя федя и наташа вместе съели 20 блинов

Смарт кенгуру 2021, вопросы и ответы для 3 — 4 классов

Кенгуру, официальное международное название Международный Математический Кенгуру (англ. International Mathematical Kangaroo) или «Кенгуру без границ» — международный математический конкурс-игра для школьников.

Конкурс Смарт кенгуру 2021 год, вопросы и ответы для 3 — 4 класса

1. Вася зашифровал буквы в слове СМАРТ цифрами. Что получилось?

2. Маша нарисовала пять картинок. На какой из этих картинок нет треугольника?

3. Красную ленту разрезали в 6 местах, а синюю в 5 местах. Сколько всего кусочков получилось?

4. Лиза разложила на столе несколько карточек. Сколько из этих карточек такие же, как карточка на рисунке справа?

5. Комар весит 2 миллиграмма. Сколько весят тысяча комаров?

6. На клетчатой бумаге Лена нарисовала 5 линий. Какая линия самая длинная?

7. Смартик изготовил пять линеек. На какой из них он правильно обозначил деления?

8. В гостях у бабушки Надя, Федя и Наташа вместе съели 20 блинов. Надя и Федя съели 15 блинов, а Федя и Наташа — 14. Сколько блинов съел Федя?

(А) 9 (Б) 8 (В)7 (Г) 6 (Д) 5

9. Магнитные буквы А, Б, В, Г и Д прикрепили на доску в ряд. Буквы Б и В оказались рядом, Г — рядом с В, а Д стоит правее В, но не с краю. Какая буква в этом ряду четвертая слева?

(А) А (Б) Б (В) В (Г) Г (Д) Д

10. На доске были написаны числа от 1 до 20. Никита стер все нечетные числа кроме тех, которые делятся на З, а затем Коля стер все четные числа кроме тех, которые делятся на 4. Сколько чисел осталось?

(А) 6 (Б) 8 (В) 10 (Г) 12 (Д) 16

11. Квадратный лист бумаги, белый с одной стороны и закрашенный с другой, разрезали на части так, как показано на рисунке. Какую из фигур можно сложить из этих частей?

12. На рисунке изображена схема. Известно, что ее можно правильно заполнить числами. Какое действие может быть записано вместо знака вопроса?

13. Миша и Лёня смотрели мультфильм. Каждый мальчик смотрел по 20 минут. Миша смотрел с начала, но не до конца, а Лёня — не с начала, зато до конца. Вместе они смотрели мультфильм 5 минут, Сколько минут длился мультфильм?

A) 20 Б) 25 B) 35 Г) 40 Д) 45

14. В каждую клетку на рисунке нужно вписать по одной цифре так, чтобы получилось верное равенство. Сколько различных равенств можно получить?

А. 1 Б) 2 B) 3 Г) 4 Д) 5

15. У Димы на 12 машинок больше, чем у Андрея, а у Андрея в 4 раза меньше, чем у Димы. Сколько всего машинок у мальчиков?

(А) 15 (Б)16 (В) 18 (Г) 20 (Д) 24

16. Из цифр 2, О, 2, 1 можно составить дату (число и месяц), например, 02.12 — это 2 декабря. Сколько всего дат, считая эту, можно составить из этих четырех цифр?

A) 3 Б) 4 В. 5 Г) 6 Д) 7

Задачи, оцениваемые в 5 баллов

17. У Кости есть монеты: по 2 рубля, по 5 рублей и по 10 рублей, всего 20 монет. На все эти деньги он купил мячик за 135 рублей. Сколько монет по 5 рублей у него бЫЛО?
(А) 1 (Б)3 (В)5 (Г) 7 (Д) 9

18. На рисунке справа изображена карточка. Четыре таких карточки положили на стол так, что получился квадрат 3х3. Какая картинка не могла получится?

А Б В Г (Д) все четыре картинки могли получиться

19. На рисунке изображен план деревни, Почтальон вышел из дома 1 и, двигаясь по дорожкам, посетил все дома в таком порядке: 2, З, 4, 5 и 6. Ни на одном перекрестке он не побывал дважды. На каком из перекрестков А—Д он мог не побывать?

(А) А (Б) Б (В) В (Г) Г (Д) Д

20. В ребусе одинаковые цифры обозначены одинаковыми буквами, а разные — разными. Известно, что С = 1. Какую цифру обозначает буква А?

(А) 8 (Б) 6 (В) 4 Г. 3 (Д) 0

Уважаемые посетители, вопросы в скором времени дополнятся. Если у Вас есть свои вопросы либо Вы заметили ошибку, пожалуйста сообщите. Заранее спасибо

Источник

Смарт кенгуру 2021, вопросы и ответы для 5 — 6 классов

Кенгуру, официальное международное название Международный Математический Кенгуру (англ. International Mathematical Kangaroo) или «Кенгуру без границ» — международный математический конкурс-игра для школьников.

В России конкурс впервые был проведен в 1994 году по инициативе Санкт-Петербургского Математического общества. Начиная с 1995 года проведением конкурса руководит Российский оргкомитет, созданный в Санкт-Петербурге при Институте продуктивного обучения Российской академии образования. Деятельность оргкомитета поддерживается Санкт-Петербургским Математическим обществом и Российским государственным педагогическим университетом им. А. И. Герцена. Непосредственную организационную работу ведет Центр технологии тестирования «Кенгуру плюс».

Конкурс Смарт кенгуру 2021 год, вопросы и ответы для 5 — 6 классов

1. На рисунке справа показа ключ к шифру. Какое число шифрует слово КЕНГА?

2. В каком числе не все цифры нечётные?

3. Из каких двух фигур 1, 2, 3, 4 можно сложить фигуру, изображенную на рисунке справа?

4. На далёкой планете Трям позавчера и послезавтра это один и тот же день недели. Сколько дней в неделе на этой планете?

5. Взглянув на часы, Знайка сказал: сейчас середина третьей четверти суток. Который сейчас час?

6. Жук-короед за день съедает 5 г древесины. Сколько таких жуков надо посадить на деревянную садовую скамейку весом 5 кг, чтобы они съели её за один день?

7. Федя изобрёл новую операцию «преуменьшение»: aөb=a-2b. Известно, что 50 өb = 10. Чему равно b?

А. 10 Б. 15 В. 20 Г. 30 Д. 40

8. На клетчатой бумаге Лена нарисовала пять многоугольников А-Д. У какого многоугольника периметр самый большой?

Задачи, оцениваемые в четыре балла

9. Женя, Федя и Ульяна вместе съели 40 конфет. Федя съел на 8 конфет больше Жени, а Ульяна — на три меньше Феди. Сколько конфет съела Ульяна?

А) 17 Б) 14 В) 10 Г) 9 Д) 7​

10. Пять друзей выстроились в ряд по росту. Известно что Андрей ниже Димы, но выше Володи, Боря и Володя не стоят рядом, Гриша не стоит рхэж,

А. Андрей Б. Боря В. Володя. Г. Гриша. Д. Дима

11. Робот Федя умеет двигаться вверх, вправо, и делать ходы во всех диагональных направлениях. Он начал с клетки, отмеченной звездочкой. В какую клетку лабиринта он не может попасть?

A) A Б) Б B) В Г) Г Д. Д

12. Четыре салфетки размера 4 х 4 положили так, что получился квадрат 6 х 6. Чему равна площадь, покрытая в четыре слоя?

A) 4 Б) 6 B) 9 Г) 10 Д) 12

13. Отрезок ОЕ длины 1 разделен на 5 равных частей. На каком отрезке находится такая точка М, что длина отрезка ОМ равна 4/7?

A) ОА Б) АВ B) ВС Г) СD Д) DЕ

14. В записи даты 20 января 2021 года (2001 2021) сумма числа и месяца равна двузначному числу, образованному двумя последними цифрами года: 20 + 1 = 21. Назовем такие даты интересными. В каком ближайшем году не будет интересной даты?

(А) 2032. (Б) 2040. (В) 2041.

15. На рисунке изображена схема. Известно, что ее можно заполнить числами так, чтобы она стала верна. Какое действие может быть написано вместо знака вопроса?

A) : 3 Б) — 17 B) : 4 Г) — 30 Д) — 24

16. В числе 1234 пары соседних цифр образуют числа 12 23 и 34. Вася написал самое маленькое число в котором среди пар соседних цифр встречаются все числа от 11 до 15. Сколько цифщ в Васином числе?

А. 6. Б. 7. В. 8. Г. 9. Д.10

17. На шахматном турнире молодой гроссмейстер Кеша должен был сыграть 15 партий. В какой-то момент он заметил, что выиграл четверть сыгранных партий, проиграл треть и остальные сыграл вничью. Сколько еще партий осталось сыграть Кеше?

A) 2 Б) 3. B) 4 Г) 5 Д) 6

18. Почтальон вышел из дома 1 и, двигаясь по дорожкам, посетил остальные дома в таком порядке: 2, 3, 4, 5. Ни на каком перекрестке он не побывал дважды. На каком из перекрестков А-Г он обязательно побывал?

(Д) на каждом из перекрестков А-Г он мог не побывать

19. На каждой клетке квадрата 3×3 Федя построил башенку из кубиков. Каждая башенка либо состоит из одного кубика, либо в ней закрашенные и белые кубики чередуются. Сколько кубиков использовал Федя, если спереди его конструкция выглядит так, как показано на рисунке?

(A) 12. (Б) 18. (B) 24. (Г) 36

(Д) такое невозможно

20. В ребусе разные буквы соответствуют разным цифрам, одинаковые — одинаковым. Какая цифра не использована?

A) 0 Б) 2 B) 5 Г) 7 Д) 9

Уважаемые посетители, вопросы в скором времени дополнятся. Если у Вас есть свои вопросы либо Вы заметили ошибку, пожалуйста сообщите. Заранее спасибо

Источник

Задачи ВПР 4 класс по математике

В конце 4 класса все ученики пишут ВПР — Всероссийские проверочные работы. Работы большие комплексные, включают в себя проверку знаний по основным предметам: русский язык, математика и окружающий мир.

В рамках данной статьи хочу остановиться на ВПР по математике. В этой работе четвероклассники сталкиваются с несколькими видами задач. Некоторые из них стандартные, встречающиеся в большинстве учебников.

Это геометрические задачи, идущие под №5, на нахождение периметра и площади данной фигуры.

Задачи №4 связаны с календарем, временем.

Задачи №8 чуть посложнее, но также являются обычными. Их решение не вызывает у детей особой сложности. Примеры задач №8:

Задачи №3 и №6 приближены к реальным жизненным ситуациям, в которых ребенку необходимо брать информацию из рисунка или таблицы.

Как показывает практика, решение этих типов задач легко осваивается детьми.

Наибольшую сложность вызывают задачи, идущие под №9 и №12. Они нестандартные, требуют умение рассуждать.

Решение задач под №12 я подробно разобрала в статье «Логические задачи для 4 класса по математике».

В данной статье хочу остановиться на задачах, встречающихся под номером 9.1 и 9.2. Данные задачи носят не столько математический, сколько аналитический характер. Без предварительной тренировки и выработанного алгоритма решение таких задач даётся детям с трудом.

Подобные задания чаще можно встретить в математических олимпиадах, нежели в учебниках по математике. При решении этих задач требуется умение рассуждать, объяснять, сравнивать, обобщать данные, делать выводы.

Рассмотрим самые интересные и трудные задачи из ВПР 4 класса, идущие под №9. Все задания были взяты с официального сайта.

Нестандартные задачи по математике 4 класс с решением и ответамиЗадача №1

Олеся, Надя и Юра бросали баскетбольный мяч в корзину. Каждый сделал 6 бросков. Все попали мячом в корзину разное число раз, а всего оказалось 13 попаданий. Надя попала мячом в корзину больше всех.

2. Известно, что Юра попал мячом в корзину всего на один раз больше, чем Олеся. Сколько раз попала мячом в корзину Олеся?

Задача №2

У Саши есть конфеты: 6 мятных, 8 лимонных и 4 вишнёвых. Саша хочет разложить все конфеты в несколько пакетиков так, чтобы в каждом пакетике встречались конфеты всех трёх видов и чтобы во всех пакетиках конфет было одинаковое количество.

Но так как у Саши всего 6+8+4=18 конфет, а 18 не делится на 4 без остатка. Значит число пакетов будет меньше. Предположим, что число пакетов 3.

3 меньше 4 и 18 делится на 3 без остатка.

2. Саша разложил все конфеты в три пакетика, причём в каждом пакетике есть конфеты всех трёх видов и количество конфет в пакетиках одинаковое. Оказалось, что в одном из пакетиков четыре лимонные конфеты. Сколько вишнёвых конфет в этом пакетике?

И еще аналогичная задача.

У Коли есть конфеты: 8 мятных, 5 лимонных и 11 клубничных. Коля хочет разложить все конфеты в несколько пакетиков так, чтобы в каждом пакетике были конфеты всех трёх видов и чтобы во всех пакетиках конфет было одинаковое количество.

2. Коля разложил все конфеты в три пакетика, причём в каждом пакетике есть конфеты всех трёх видов и количество конфет в пакетиках одинаковое. Оказалось, что в одном из пакетиков шесть мятных конфет. Сколько клубничных конфет в этом пакетике?

Задача №3

У Вали есть конфеты: 6 апельсиновых, 7 клубничных, 6 лимонных и 5 вишнёвых. Валя хочет разложить все конфеты в несколько пакетиков так, чтобы ни в одном пакетике не было двух одинаковых конфет и чтобы во всех пакетиках конфет было одинаковое количество.

Предлагаю решить эту задачу наглядно, разложив действия на понятные детям этапы.

Найдем число всех конфет 6+7+6+5=24 штуки.
Так как конфет 4 вида, то попробуем разложить по 4 конфеты в каждый пакет.
24:4=6 пакетов получится.

Но клубничных конфет 7, значит по 4 конфеты раскладывать нельзя, т.к. иначе в один пакет попадут две одинаковые конфеты, а это противоречит условию задачи.

Попробуем разложить по 3 конфеты.
24:3=8 пакетов получится.
Сначала разложим конфеты, которых меньше всех, т.е. вишневых.

Затем начинаем докладывать другие конфеты, но начиная с тех пакетиков, где конфет меньше. Сначала разложим, например, апельсиновые конфеты.

Затем клубничные, но опять же, начиная с тех пакетиков, где конфет меньше.

У нас осталось 6 лимонных конфет и 6 пакетиков по 2 конфеты. В них и докладываем лимонные конфеты.

Таким образом, мы разложили все 24 конфеты, в каждом пакетике нет двух одинаковых конфет и во всех пакетах одинаковое количество конфет.
Если бы мы раскладывали по 2 конфеты, то пакетов вышло бы больше, а нам, по условию задачи, нужно получить наименьшее число пакетиков.
Ответ: 8 пакетов.

2. Валя разложила все конфеты в восемь пакетиков, причём конфет во всех пакетиках одинаковое количество и ни в одном пакетике нет двух одинаковых конфет. Сколько у неё получилось пакетиков, в которых есть и апельсиновая, и клубничная, и лимонная конфета?

Аналогичные задачи для самостоятельного решения.

У Тани есть конфеты: 6 апельсиновых, 7 клубничных, 8 лимонных и 9 вишнёвых. Таня хочет разложить все конфеты в несколько пакетиков так, чтобы ни в одном пакетике не было двух одинаковых конфет и чтобы во всех пакетиках конфет было одинаковое количество.

У Серёжи есть конфеты: 11 апельсиновых, 7 клубничных, 10 лимонных и 8 вишнёвых. Серёжа хочет разложить все конфеты в несколько пакетиков так, чтобы ни в одном пакетике не было двух одинаковых конфет и чтобы во всех пакетиках конфет было одинаковое количество.

У Вити есть конфеты: 6 апельсиновых, 7 клубничных, 9 лимонных и 8 вишнёвых. Витя хочет разложить все конфеты в несколько пакетиков так, чтобы ни в одном пакетике не было двух одинаковых конфет и чтобы во всех пакетиках конфет было одинаковое количество.

Задача №4

Алексей Владимирович едет читать лекции в города Дальнего Востока на неделю, с понедельника по воскресенье включительно. Он посетит по порядку города: Биробиджан, Хабаровск, Владивосток и Южно-Сахалинск. В каждом городе Алексей Владимирович планирует читать лекции не более двух дней, а переезжать из города в город будет только ночью.

Используя все условия задачи, решение удобно оформить в виде таблицы. Понятно, что в одном из городов Алексей Владимирович будет находиться не два, а один день. Рассмотрим все варианты.

Из данных таблицы однозначно понятно, что в пятницу будет лекция во Владивостоке.

2.Если ночь с четверга на пятницу Алексей Владимирович проведёт в гостинице, то в каком городе он будет читать лекцию в субботу?

Задача №5

Семёну Олеговичу нужно посетить трёх врачей в поликлинике: стоматолога, эндокринолога и окулиста. Он пришёл в поликлинику к 11 часам и выяснил, что окулист может принять с 12 до 13 часов, эндокринолог – с 9 до 13 часов, а стоматолог – с 11 до 14 часов. Семёну Олеговичу удалось посетить всех трёх врачей и провести у каждого ровно по часу.

1. У какого врача Семён Олегович был в 11:30?

По условию задачи, врачи начинают прием с 11 часов:
окулист — с 12 до 13 часов (1 час),
эндокринолог – с 11 до 13 часов (3 часа),
стоматолог – с 11 до 14 часов (3 часа).
Очевидно, что к окулисту можно попасть только с 12 до 13 часов, ибо он работает только 1 час и другой возможности его посетить просто нет.
Тогда имеем:
эндокринолог – с 11 до 12 часов,
стоматолог – с 13 до 14 часов.

Ответ: В 11 30 Семен Олегович был у эндокринолога.

2. К какому врачу Семён Олегович пошёл после приёма окулиста?

Аналогичные задачи для самостоятельного решения.

Татьяна должна обсудить свою новую идею с директором, бухгалтером и программистом. С каждым из них обсуждение длится ровно час. Известно, что директор занят с 10 до 12 часов, бухгалтер приезжает на работу к 10 часам, а у программиста важное совещание с 10 до 11 часов. При этом Татьяна смогла закончить все три обсуждения к 12 часам, придя на работу к 9 часам.

Менеджер Наталья обсуждала свою новую идею с начальником отдела продаж, юристом и программистом. Каждое из обсуждений длилось ровно 45 минут с перерывами по 15 минут между ними. Известно, что юрист приехал в офис к 10:30, а у начальника отдела продаж было важное совещание с 9:00 до 10:00. При этом Наталья смогла закончить все три обсуждения к 12:00, начав первое из них в 9:15.

Задача №6

Артур приехал в Екатеринбург в понедельник и планирует пробыть там до субботы. Он хочет сходить в театр, встретиться с одноклассниками и посетить музей, причём каждому из этих дел он хочет посвятить отдельный день. Спектакль, который Артур хочет посмотреть в театре, идёт только по вторникам и четвергам, музей работает только по средам, а одноклассники могут встретиться с Артуром в среду или четверг.

1. Куда Артур пойдёт в четверг?

2. Куда пойдёт Артур за день до похода в музей?

Аналогичная задача.

Дина приехала в Челябинск во вторник и планирует пробыть там до воскресенья. Она хочет встретиться с подругой, посетить концерт любимой музыкальной группы, сходить в музей и сходить в театр, причём каждому из этих дел она хочет посвятить отдельный день, концерт её любимой группы проводится только в четверг, музей работает со среды по субботу, спектакли в театре идут в среду и пятницу, подруга свободна в четверг и пятницу.

Задача №7

Рома, Оля и Паша съели вместе 13 конфет. Больше 8 конфет не съел никто. Паша съел больше всех конфет, а Оля съела на 2 конфеты больше, чем Рома.

1. Сколько конфет съел Паша?

Из условия задачи понятно, что Рома съел меньше всех конфет. Рассмотрим варианты.

Если Рома съел 1 конфету, тогда Оля съела 3 конфеты, а Паша съел 9 конфет, чего быть не может.
Если Рома съел 2 конфеты, тогда Оля съела 4 конфеты, а Паша съел 7 конфет, это соответствует условиям задачи.
Если Рома съел 3 конфеты, тогда Оля съела 5 конфет, а Паша съел 5 конфет, чего быть не может.

Ответ: Паша съел 7 конфет.

2. Сколько конфет съела Оля?

Аналогичные задачи для самостоятельного решения.

Аня, Боря и Вера съели вместе 14 конфет. Больше 8 конфет не съел никто. Аня съела больше всех конфет, а Боря съел на 1 конфету больше, чем Вера.

Задача №8

2. Сколько грибов нашёл Юра?

Маша и Юра вместе набрали 8 грибов. Маша набрала грибов меньше, чем Юра и при этом не меньше 3.
Предположим Маша нашла 4 или более грибов, но это будет противоречить условию, что Юра набрал больше.
Предположим, что Маша нашла 3 гриба, тогда Юра 8-3=5 грибов — это соответствует всем условиям.
Ответ: Юра нашёл 5 грибов.

Витя, Федя и Лена ходили за грибами. Витя собрал 12 грибов, Федя собрал на 5 грибов меньше, чем Витя и Лена вместе. Один из троих ребят собрал 6 грибов.

Если 6 грибов собрал Федя, то по условию Витя и Лена собрали на 5 грибов больше, т.е. 6+5=11, что невозможно, поскольку только один Витя собрал 12 грибов. Значит 6 грибов собрала Лена.

Тогда Федя собрал 12+6-5=13 грибов.
Ответ: 6 грибов Лена и 13 грибов Федя.

Надеюсь, что данная статья была для вас полезна и понятна. Пишите комментарии.

Подробный разбор решений самых сложных задач, идущих под №12 в ВПР 4 класса по математике можно посмотреть в статье «Логические задачи из ВПР 4 класс по математике».

С уважением, Ольга Наумова

Заходите в Книжную лавку за полезными книгами!

Благодарю, что поделились статьей в социальных сетях!

Источник

ЗАДАЧИ МЕЖДУНАРОДНОГО КОНКУРСА «Кенгуру»

19 марта 2015 г. 3–4 классы

Задачи, оцениваемые в 3 балла

№1. Незнайка писал слово КЕНГУРУ. У него получилось: Сколько букв он написал неправильно?

(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

№2. Чему равна сумма двадцати сотен и пятнадцати?

(A) 35 (Б) 215 (В) 2015 (Г) 20015 (Д) 200015

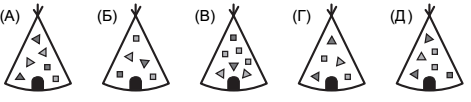
№3. Индеец Белый Орёл живет в вигваме, на котором треугольников и квадратиков нарисовано поровну. На каком из рисунков изображён его вигвам?

№4. Что не равно 12?

(Б) число месяцев в году

(В) число часов в сутках

(Г) утроенный номер этой задачи

(Д) число подвигов Геракла

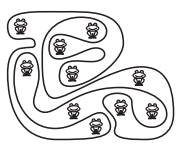
№5. На рисунке изображён пруд и несколько лягушек. Сколько из этих лягушек сидят в пруду?

(A) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9

№6. В числе 2015 четыре цифры. Произведение двух бóльших цифр поделили на сумму двух меньших. Что получилось?

(A) 6 (Б) 7 (В) 8 (Г) 10 (Д) 15

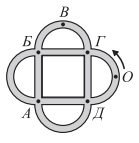
№7. Петя катается на велосипеде по дорожкам, изображённым на рисунке. Он стартует из точки О в направлении, указанном стрелкой. На первом перекрёстке Петя поворачивает направо, на втором — налево, потом опять направо, потом опять налево, и так далее. В какой точке он не может оказаться?

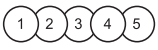
№8. Аня отметила на прямой линии 5 красных точек. В каждый промежуток между красными точками она поставила синюю точку, а потом в каждый промежуток между красной и синей точками — зелёную точку. Сколько всего точек получилось?

(A) 9 (Б) 15 (В) 17 (Г) 18 (Д) 20

№9. Аня, Боря, Вася, Гриша и Дима написали на доске числа 1, 3, 4, 6 и 8, каждый по одному числу. Васино число оказалось в 2 раза больше, чем Димино, а Борино — на 2 больше, чем Гришино. Какое число написала Аня?

(A) 8 (Б) 6 (В) 4 (Г) 3 (Д) 1

№10. Тысяча дециметров равна

(A) 10 км (Б) 1 км (В) 100 м (Г) 10 м (Д) 1 м

Задачи, оцениваемые в 4 балла

№11. С первого января 2015 года малыш Федя начал вести дневник. Он уверен, что в каждом месяце ровно 30 дней. Какую дату он напишет в своем дневнике 19 марта 2015 года в день конкурса «Кенгуру»?

(A) 17 марта (Б) 18 марта (В) 19 марта (Г) 20 марта (Д) 21 марта

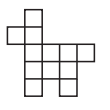
№12. Маша хочет разрезать по сторонам клеточек прямоугольник 4×3 так, чтобы из полученных частей можно было сложить фигурку, изображённую справа. На какое наименьшее число частей придётся разрезать прямоугольник?

(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6

№13. Вася наклеил на лист бумаги одну за другой 5 круглых наклеек с цифрами. В каком
порядке он не мог их наклеивать?

(A) 3, 2, 5, 4, 1 (Б) 5, 3, 4, 2, 1 (В) 3, 5, 1, 2, 4 (Г) 5, 3, 2, 4, 1 (Д) 3, 2, 1, 5, 4

№14. Друзья выясняли, какой сегодня день недели. Витя сказал: «Вчера было воскресенье». Сема сказал: «Завтра будет суббота». Петя сказал: «Позавчера была пятница». Саша сказал: «Послезавтра будет среда». Двое из них ошиблись. Какой сегодня день недели?

(A) понедельник (Б) вторник (В) среда (Г) четверг (Д) суббота

№15. Какой из результатов самый маленький?

(A) (100 − 1) : 9 (Б) (1000 − 10) : 9 (В) (1000 − 1) : 9 (Г) (1000 − 100) : 9 (Д) (100 − 10) : 9

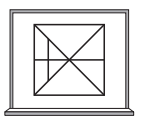
№16. Наташа рассматривает в лупу разные части рисунка на школьной доске. Какое из изображений А–Д она не сможет увидеть?

№17. Разность двух чисел на 3 меньше уменьшаемого и на 4 больше вычитаемого. Чему она равна?

(A) 7 (Б) 9 (В) 10 (Г) 12 (Д) 15

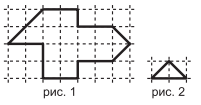
№18. Фигуру, изображённую на рис. 1, Вася разрезал на одинаковые треугольники, изображённые на рис. 2. Сколько треугольников у него получилось?

(A) 8 (Б) 12 (В) 14 (Г) 15 (Д) 16

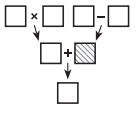
№19. Стрелочки на рисунке указывают на результаты действий с числами. Числа 1, 2, 3, 4, 5, 6 и 7 надо разместить по одному в квадратиках так, чтобы все результаты были правильными. Какое
число попадёт в заштрихованный квадратик?

(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

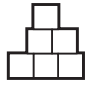
№20. Фигура на рисунке состоит из одинаковых квадратов со стороной 1 см. Чему равен её периметр?

(A) 9 см (Б) 10 см (В) 11 см (Г) 12 см (Д) невозможно определить

Задачи, оцениваемые в 5 баллов

№21. Маша заполняет горшочек крупой. Он будет полным, если в него насыпать 6 чайных ложек, 3 десертных и 1 столовую ложку крупы или 2 чайные ложки, 1 десертную и 3 столовые ложки той же крупы. У Маши есть только столовые ложки. Сколько таких ложек крупы ей придется насыпать?

(A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8

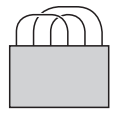
№22. У длинной верёвки связали концы и разложили получившуюся петлю на столе. Часть этой петли закрыта (смотри рисунок). Как может выглядеть закрытая часть?

№23. В гостях у бабушки Женя и Лена ели мороженое ежедневно: каждая по 2 или 3 стаканчика. Всего Женя съела 25 стаканчиков, а Лена — 19. Сколько дней они гостили у бабушки?

(A) 8 (Б) 9 (В) 10 (Г) 11 (Д) 12

№24. В числовом ребусе буквами O, D, E, V, N обозначены разные цифры. Сколько различных цифр может обозначать буква V?

(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

№25. Дима, Федя, Надя и Катя пошли в лес за грибами. Известно, что Дима нашел грибов меньше, чем Федя, мальчики нашли грибов столько же, сколько девочки, а Дима и Надя нашли грибов больше, чем Федя и Катя. Кто нашел больше всех грибов?

(A) Дима (Б) Федя (В) Катя (Г) Надя (Д) невозможно определить

№26. Никита выписывает подряд целые числа 1, 2, 3,…, но он не любит цифру 7 и пропускает все числа, которые её содержат. Он выписал 777 чисел. Какое число он написал последним?

(A) 888 (Б) 1000 (В) 1053 (Г) 1333 (Д) 1631

Источник