в каком числе содержится 2 раза по 9

Ответы. Учебник. Часть 2 (с. 56)

Мар 19

Ответы. Учебник. Часть 2 (с. 56)

Числа от 1 до 100
Умножение и деление

1. Используя это свойство умножения, найди значение второго выражения в каждой паре, зная значение первого.

4 • 5 = 20 7 • 4 = 28 9 • 3 = 27
5 • 4 = 20 4 • 7 = 28 3 • 9 = 27

2. В школьном саду 3 ряда кустов смородины, по 5 кустов в каждом ряду. Сколько всего кустов смородины в школьном саду?
Сделай схематический рисунок и реши задачу.

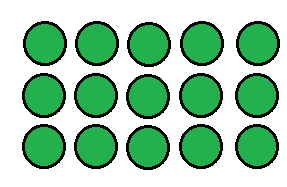
5 • 3 = 15 (к.)
О т в е т : 15 кустов смородины в школьном саду.

3. Найди периметр квадрата со стороной 25 мм.

25 • 4 = 100 (мм)
О т в е т: 100 мм периметр квадрата.

4. На сколько 54 больше, чем 8, 19, 36, 42?

54 − 8 = 46 − 54 больше, чем 8, на 46 единиц;
54 − 19 = 35 − 54 больше, чем 19, на 35 единиц;
54 − 36 = 18 − 54 больше, чем 36, на 18 единиц;
54 − 42 = 12 − 54 больше, чем 42, на 12 единиц.

65 − 13 = 52 58 + 19 = 77
65 + 13 = 78 35 + 15 = 50

6. Сколько раз по 3 содержится в числе 6? в числе 9? в числе 12?

6 − 3 − 3 = 0;
9 − 3 − 3 − 3 = 0;
12 − 3 − 3 − 3 − 3 = 0;
15 − 3 − 3 − 3 − 3 − 3 = 0.

В числе 6 содержится 2 раза по 3.
В числе 9 содержится 3 раза по 3.
В числе 12 содержится 4 раза по 3.

7. Найди значения выражений a − 7 и a + 8 при: a = 23, a = 57, a = 60, a = 92.

7 • 4 = 4 • 7 3 • 5 > 3 • 4 13 • 2 = 2 • 13

ЗАДАНИЕ НА ПОЛЯХ:
Сколько прямоугольников?

Источник

ГДЗ по математике 2 класс проверочные работы Волкова, Моро — страница 14

Подготовили готовое домашнее задание к упражнениям на 14 странице по предмету математика за 2 класс. ➜ Ответы на задания: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11.

Проверочные работы — Страница 14.

Тест 2 (вариант 1)

Заполни пропуски верными числами, словами.

Число 59 при счете стоит между числами ☐☐ и ☐☐.

Ответ: число 59 при счете стоит между числами 58 и 60.

Между числами 39 и 43 в числовом ряду стоят числа:

В числе 68 содержится ☐ десятков и ☐ единиц.

Ответ: в числе 68 содержится 6 десятков и 8 единиц.

Если число 79 увеличить на ☐, то получится 80

Ответ: если число 79 увеличить на 1, то получится 80.

В числе ☐☐ содержится 3 десятка и 5 единиц.

Ответ: в числе 35 содержится 3 десятка и 5 единиц.

Если число ☐☐ уменьшать на 1, то получится 48.

Ответ: если число 49 уменьшить на 1, то получится число 48.

Число 87 можно записать как сумму разрядных слагаемых так:

Ответ: 8 десятков + 7 единиц, или 80 + 7

Число 19 меньше, чем число ☐☐, на 9.

Ответ: число 19 меньше, чем число 28, на 9.

Вычисли и запиши сумму чисел: 30 + 8

Если уменьшаемое 46, а вычитаемое 40, то ________________ равна ☐.

Ответ: если уменьшаемое 46, а вычитаемое 40, то разность равна 6.

Из цифр 6, 7, 8, выбери и запиши в каждое окошко одну и ту же цифру, такую, чтобы неравенство 8☐ Рейтинг

Источник

Разряды и классы чисел

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Названия классов многозначных чисел справа налево:

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:

А теперь прочитаем число единиц каждого класса слева направо:

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.

Разрядные единицы обозначают так:

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Источник

В каком числе содержится 2 раза по 9

Числа от 1 до 1000
Итоговое повторение всего изученного
Арифметические действия
Умножение и деление

Ответы к стр. 92

1. В каком случае сложение можно заменить умножением? Покажи на примерах.

Умножением можно заменить сумму одинаковых слагаемых, например:
4 + 4 + 4 = 4 • 3 = 12
5 + 5 + 5 + 5 + 5 + 5 = 5 • 6 = 30

2. Какими знаками обозначаются умножение и деление и как называются выражения, в которых числа соединены знаком умножения? знаком деления?

Знак умножения: точка – •, знак деления: двоеточие – :.
25 • 4 — произведение, 60 : 5 — частное.

3. Покажи, как умножение можно заменить сложением.
7 • 3 38 • 4 156 • 2 9 • 6

7 • 3 = 7 + 7 + 7 = 21
38 • 4 = 38 + 38 + 38 + 38 = 152
156 • 2 = 156 + 156 = 312
9 • 6 = 9 + 9 + 9 + 9 + 9 + 9 = 54

4. Вставь знак >, Читайте также: Какие микроэлементы содержатся в сыре

1) Чтобы проверить результат умножения, нужно произведение разделить на один из множителей. Чтобы проверить деление, можно частное умножить на делитель или делимое разделить на частное.
2) 356 • 8 = 2848 Проверка:
2848 : 356 = 8
2848 : 8 = 356

45360 : 9 = 5040 Проверка:
5040 • 9 = 45360
45360 : 5040 = 9

ЗАДАНИЕ НА ПОЛЯХ
РЕБУС

9 • 7 = 63
9 • 3 = 27
9 • 8 = 72
8 • 3 = 24
(8 • 8 = 64)
7 • 3 = 21
6 • 5 = 3
4 • 7 = 28

Ответы по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Источник

В каком числе содержится 2 раза по 9

Опубликовано 1 год назад по предмету
Математика
от Аккаунт удален

Ответ дан
JonuZoiv

Нужно 3 умножить на 9 будет 27

Ответ дан
Аккаунт удален

Ответ дан
JonuZoiv

Ответ дан
Alice098

27, нет? 3 умножаем на 9, получается 27

Не тот ответ, который вам нужен?

Самые новые вопросы

Математика – 7 месяцев назад

Сколько здесь прямоугольников

История – 1 год назад

Какое управление было в древнейшем риме? как звали первого и последнего из царей рима?

Литература – 1 год назад

Русский язык – 1 год назад

Помогите решить тест по русскому языку тест по русскому языку «местоимение. разряды местоимений» для 6 класса
1. укажите личное местоимение:
1) некто
2) вас
3) ни с кем
4) собой
2. укажите относительное местоимение:
1) кто-либо
2) некоторый
3) кто
4) нам
3. укажите вопросительное местоимение:
1) кем-нибудь
2) кем
3) себе
4) никакой
4. укажите определительное местоимение:
1) наш
2) который
3) некий
4) каждый
5. укажите возвратное местоимение:
1) свой
2) чей
3) сам
4) себя
6. найдите указательное местоимение:
1) твой
2) какой
3) тот
4) их
7. найдите притяжательное местоимение:
1) самый
2) моего
3) иной
4) ничей
8. укажите неопределённое местоимение:
1) весь
2) какой-нибудь
3) любой
4) этот
9. укажите вопросительное местоимение:
1) сколько
2) кое-что
3) она
4) нами
10. в каком варианте ответа выделенное слово является притяжательным местоимением?
1) увидел их
2) её нет дома
3) её тетрадь
4) их не спросили

Русский язык – 1 год назад

Переделай союзное предложение в предложение с бессоюзной связью.
1. океан с гулом ходил за стеной чёрными горами, и вьюга крепко свистала в отяжелевших снастях, а пароход весь дрожал.
2. множество темноватых тучек, с неясно обрисованными краями, расползались по бледно-голубому небу, а довольно крепкий ветер мчался сухой непрерывной струёй, не разгоняя зноя
3. поезд ушёл быстро, и его огни скоро исчезли, а через минуту уже не было слышно шума

Русский язык – 1 год назад

помогите прошу!перепиши предложения, расставляя недостающие знаки препинания. объясни, что соединяет союз и. если в предложении один союз и, то во втором выпадающем списке отметь «прочерк».пример:«я шёл пешком и,/поражённый прелестью природы/, часто останавливался».союз и соединяет однородные члены.ночь уже ложилась на горы (1) и туман сырой (2) и холодный начал бродить по ущельям.союз и соединяет:1) части сложного предложенияоднородные члены,2) однородные членычасти сложного предложения—.поэт — трубач зовущий войско в битву (1) и прежде всех идущий в битву сам (ю. янонис).союз и соединяет:1) части сложного предложенияоднородные члены,2) ​

Физика – 1 год назад

Вокруг прямого проводника с током (смотри рисунок) существует магнитное поле. определи направление линий этого магнитного поля в точках a и b.обрати внимание, что точки a и b находятся с разных сторон от проводника (точка a — снизу, а точка b — сверху). рисунок ниже выбери и отметь правильный ответ среди предложенных.1. в точке a — «от нас», в точке b — «к нам» 2. в точке a — «к нам», в точке b — «от нас» 3. в обеих точках «от нас»4. в обеих точках «к нам»контрольная работа по физике.прошу,не наугад важно

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

ЗАДАНИЯ ДЛЯ ПОДГОТОВКИ К ОЛИМПИАДЕ ПО МАТЕМАТИКЕ В 5 КЛАССЕ

1. На полке в один ряд стоят книги. Энциклопедия стоит пятой слева и семнадцатой справа. Сколько книг на полке?

2. Двое поделили между собой 7 рублей, причем один из них получил на 3 рубля больше другого. Сколько кому досталось?

Ответ. Одному — 2 рубля, другому — 5 рублей.

3. Число 2002 “симметричное”, т.е. читается одинаково слева-направо и справа-налево. Напишите следующее за ним симметричное число.

4. Торговец купил корову за 7 долларов, продал ее за 8, потом вновь купил ту же корову за 9 долларов и опять продал за 10. Какую прибыль он получил?

5. Напишите наименьшее 10-значное число, все цифры которого различны.

6. В коробке 14 белых и 14 чёрных шариков. Какое минимальное количество шариков нужно достать из коробки, чтобы среди них наверняка оказалось 2 черных шарика?

7. Ученики одного класса съели 95 конфет, причем каждый мальчик съел 3 конфеты, а каждая девочка — 5 конфет. Сколько в классе мальчиков и сколько девочек, если всего в классе 25 человек?

Ответ. 15 мальчиков и 10 девочек.

Ответ. Добрыня Никитич.

9. Два поезда, оба длиной 50 м, движутся навстречу друг другу со скоростью 45 км/ч. Сколько времени пройдёт от момента, когда встретятся машинисты, до момента, когда встретятся проводники последних вагонов?

10. Чему равна сумма 123456789 + 234567891 + 345678912 + … + 912345678?

11. Произведение двух чисел умножили на их разность. Могло ли получиться 30?

Решение. Могло. Например: 5·2·(5 − 2) = 30.

12. Ваня, задумав некоторое число, умножил его на 2, затем к результату прибавил 3, после чего получившееся число разделил на 7, а потом, уменьшив частное на 1, сказал, что у него получилось число 2. Определите, какое число задумал Ваня.

Решение. Будем решать задачу с конца. В итоге у Вани получилось 2, значит, перед вычитанием 1 у него было 3. Аналогично перед делением на 7 у него было 21, перед прибавлением 3 — было 18, а перед умножением на 2 — было 9.

13. Расставьте в квадрате 4×4 одного короля, одного слона и двух ладей так, чтобы они не били друг друга.

Решение. Например, так:

14. Есть 100 комнат и 100 мальчиков, каждый из которых находится в одной из комнат. На двери каждой комнаты написано: “Тут ровно один мальчик”. Известно, что среди этих надписей есть ровно три неверные. Докажите, что в одной из комнат находятся три мальчика.

Решение. Так как из ста надписей ровно 3 неверные, то 97 из них верные. Значит, в этих 97 комнатах по одному мальчику. Тогда в остальных трёх комнатах с неверными надписями всего 3 мальчика. При этом ни в какой из этих трёх комнат не может быть ровно один мальчик, так как иначе надпись на такой комнате будет верной. Трёх мальчиков можно распределить по трём комнатам следующими способами: 3 − 0 − 0, 2 − 1 − 0, 1 − 1 − 1. Последние два варианта не подходят, поэтому в какой-то комнате точно находятся три мальчика.

15. Можно ли расположить по кругу числа 1, 2, …, 8 так, чтобы сумма любых трёх рядом стоящих чисел была больше 13?

Решение. Нельзя.
Предположим, что такая расстановка возможна. Рассмотрим все возможные тройки подряд стоящих чисел. Каждое число войдёт ровно в три такие тройки, и в каждой тройке сумма чисел должна быть больше 13, а значит, не меньше 14. Всего троек будет 8, тогда общая сумма чисел в них будет не меньше, чем 14·8 = 112. В эту сумму каждое из выписанных чисел входит по три раза. Тогда получается, что сумма чисел от 1 до 8 равна числу, которое не меньше, чем 112⁄3 > 37. Но 1 + 2 + … + 8 = 8·9⁄2 = 36. Противоречие, значит указанной в условии расстановки не существует.

Занятие 2.Плюс-минус один

1. Зайцы нашли в лесу бревно длиной 6 м. Чтобы отнести домой, они распилили его на части длиной по 1 метру. Сколько они сделали распилов?

Решение. После каждого распила одна часть распадается на две, т.е. количество частей увеличивается на 1. В начале была одна часть (целое бревно), в итоге стало 6. Значит, было сделано 6 − 1 = 5 распилов.

2. Из книги выпал кусок, у первой страницы которого номер 35, а у последней — 74. Сколько страниц выпало?

Решение. Рассмотрим страницы с 1-й по 74-ю. Из них в выпавший кусок не входят с 1-й по 34-ю. Значит, выпало 74 − 34 = 40 страниц.

3. Теперь у зайцев уже несколько бревен. Они распили все бревна, сделав 20 распилов, и получили 27 чурбачков. Сколько бревен было у зайцев?

Решение. Так как после каждого распила количество чурбачков увеличивается на 1, то значит, после 20 распилов их количество также увеличилось на 20. Тогда изначально у зайцев было 27 − 20 = 7 брёвен.

4. Сколько всего существует двузначных чисел? А трёхзначных?

Решение. Двузначные числа — это 10, 11, 12, …, 99. Всего их 99 − 9 = 90.
Аналогично трёхзначных чисел 999 − 99 = 900.

5. Улитке надо подняться на столб высотой 10 м. Каждый день она поднимается на 4 м, а каждую ночь сползает на 3 м. Когда улитка доползёт до цели, если она стартовала в понедельник утром?

Решение. За сутки (день и ночь) улитка будет продвигаться по столбу на 1 м (подниматься на 4 м днём и опускаться на 3 м ночью). В итоге после 6 суток она окажется на высоте 6 м и за следующий день доползёт до верха.

6. Главное здание МГУ состоит из нескольких секторов. Этажи в разных секторах отличаются по высоте. Из-за этого, например, получается, что переходы с 13 этажа сектора А ведут на 19 этаж секторов Б и В. Как соотносятся по высоте этажи в этих секторах?

Решение. Уровень пола 13 этажа сектора А совпадает с уровнем пола 19 этажа секторов Б и В. Значит, высота первых 18 этажей сектора А равна высоте первых 12 этажей в Б и В. Тогда отношение равно 18:12 или 2:3.

7. Сколько раз за сутки на часах минутная стрелка обгонит часовую?

Решение. За первые 12 часов минутная стрелка обгонит часовую 10 раз: каждый час, кроме первого и последнего. В 0 ч и 12 ч стрелки совместятся. Так как мы рассматриваем промежуток времени в 24 часа, то стрелки пойдут дальше. Их совпадение в 12 ч дня тоже нужно считать обгоном.
За следующие 12 часов произойдёт ещё 10 обгонов, а всего их будет 10 + 1 + 10 = 21.

8. Для нумерации страниц в книге потребовалось 2322 цифры. Сколько страниц в этой книге?

Решение. Всего есть 9 однозначных и 90 двузначных номеров. На них приходится 9 + 2·90 = 189 цифр. Остаётся 2322 − 189 = 2133 цифр. Они образуют 2133⁄3 = 711 трёхзначных последовательных номеров. Значит, всего страниц 99 + 711 = 810.

9. В ряд выписаны все натуральные числа:
1234567891011121314151617181920…
Какая цифра стоит на 2010 месте?

Решение. Посмотрим какому числу будет принадлежать эта цифра. Первые 9 цифр относятся к однозначным числам, следующие 2·90 = 180 к двузначным. Остаётся ещё 2010 − 189 = 1821 цифра. Из них состоят 1821⁄3 = 607 трёхзначных чисел. Последнее из них будет равно 99 + 607 = 706. Значит, 2010-я цифра будет 6.

10. Серёжа купил тетрадь объемом 96 листов и пронумеровал все её страницы по порядку числами от 1 до 192. Данил вырвал из этой тетради какие-то 50 страниц и сложил все 50 чисел, которые на них написаны. Докажите, что у него не могла получиться сумма 2010.

Решение. Вырванные страницы пронумерованы 50 последовательными числами. Среди них 25 чётных и 25 нечётных. Но сумма, содержащая нечётное количество нечётных слагаемых, нечётна, а значит, 2010 быть равна не может.

учитель начальных классов

Математический диктант № 1

(3, 56, 2, 9,9, 7, 4, 5, 9, 7)

Математический диктант № 2

(45, 21, 3, 42, 7, 5, 28, 8, 27, 16)

Математический диктант № 3

(3, 5, 8, 36, 4, 64, 9, 7, 21, 10)

Математический диктант № 4

(18, 2, 4, 5, 12, 10, 4, 28, 6, 6)

Математический диктант № 5

(9, 5, 4, 56, 3, 48, 32, 64, 63, 9)

Математический диктант № 6

(28, 4, 5, 7, 4, 21, 6, 6,16, 8)

Математический диктант № 7

(8, 27, 9, 3, 72, 9, 5, 48, 36, 45)

Математический диктант № 8

(9, 54, 4, 8, 6, 1, 8, 3, 81, 6)

Математический диктант № 9

(35, 8, 56, 36, 48, 2, 5, 63, 9, 42)

Математический диктант № 10

(4, 8, 27, 72, 7, 8, 20, 21, 6, 9)

Источник