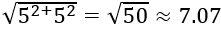в каком штате сша число пи равно 4
Как в Индиане пытались округлить число «пи»
В 1897 году в Законодательное собрание штата Индиана поступил проект закона №246, в тексте которого предлагалось округлить число «пи» до 3,2.
Гениальный Гудвин
Автором законопроекта был Эдвин Гудвин — физик и математик-любитель. Предложения Гудвина касались главным образом квадратуры круга — так называется неразрешимая математическая задача построения квадрата, равного по площади заданному кругу.
Строго говоря, Эдвин в своем законопроекте ни словом ни обмолвился о числе «пи». Но во второй части текста закона он написал: «… четвертый важный факт — отношение диаметра окружности к её длине соответствует отношению четырех к пяти четвертым». Между тем, отношение диаметра к длине окружности — это и есть число «пи».
Таким образом, Гудвин предлагал принять его значение за 4:(5/4) = 4: 1.25 = 3.2
Слушания в Палате представителей
В Палате представителей штата Индиана законопроект приняли с осторожностью. Сначала его направили на рассмотрение в Комитет по финансам, затем «отфутболили» в Комитет по образованию… Законопроект успел побывать даже в Комитете по вопросам болот. Наконец, 6 февраля 1897 года, законопроект прошел слушания в Палате представителей и был направлен для одобрения в Сенат штата.
Сенаторы Индианы оказались сообразительнее своих коллег из Палаты представителей. Они вызвали из Университета Пердью профессора математики Кларенса Вальдо. Когда Вальдо попытались познакомить с «гением, который написал этот законопроект», профессор вежливо отказался, сославшись на то, что уже неоднократно имел честь разговаривать с умалишенными. Законопроект об округлении «пи» почти прошел сенатские слушания — этого не случилось лишь благодаря усилиям Вальдо и газетчиков, поднявших на смех «гениального математика». Поэтому сейчас в штате Индиана число «пи», как и везде, равняется 3,14159265358979323… уф… может, Гудвин был не так уж и неправ?
Правда ли, что в штате Индиана число пи равно 4?
В сборниках занимательных фактов и прочей литературе нередко можно встретить утверждение о том, что в штате Индиана значение числа пи на законодательном уровне приравнено к 4 — для удобства подсчётов. Мы проверили, правда ли это.
На постсоветском пространстве этот забавный факт известен ещё со времён СССР. Например, в 1991 году он попал в отечественное издание Книги рекордов Гиннесса со ссылкой на некий Билль 246, принятый Генеральной ассамблеей штата. И в наше время эта информация появляется в различных публикациях (часто — в сборниках нелепых американских законов). Например, в «Тверском лингвистическом меридиане», журнале «Новый крокодил» и таких авторитетных источниках, как журнал «Коммерсантъ Власть» и «Парламентская газета». А вот в книге «100 великих научных достижений России» приводится другое значение константы — там утверждается, что в штате Индиана число пи равно 3,2.
О том, что число пи (π) — соотношение длины окружности к её диаметру — иррационально, то есть не может быть представлено в виде обыкновенной дроби, люди знают со школьной скамьи. Обычно в бытовых расчётах используется округлённое значение — 3,14, хотя оно совсем не подходит для более точных и важных измерений.
Но давайте сначала обратимся не к проблемам числа пи, а к такой неразрешимой задаче древности, как квадратура круга — построении с помощью циркуля и линейки квадрата, равного по площади данному кругу. Математики бились над этой проблемой много веков, однако только в 1882 году Фердинанд фон Линдеман доказал тщетность всех потенциальных усилий в этом вопросе. И если учёные земного шара довольно быстро узнали о неутешительном, но в целом довольно ожидаемом выводе, то непрофессионалы не оставляли надежд.
В 1888 году врач и математик-любитель из Индианы Эдвард (Эдвин) Джонстон Гудвин решил, что совершил открытие, и потратил несколько лет на попытки сообщить о нём миру. В преддверии Всемирной выставки в Чикаго 1893 года ему удалось договориться с организаторами о выделении павильона для «чтения научных лекций». Однако вскоре руководство выставки, ознакомившись с выкладками Гудвина, известило его о своём отказе. Математик-любитель не унывал и в июле 1894 года опубликовал статью о своей научной победе не где-нибудь, а в «Американском математическом ежемесячнике», передовом издании в своей сфере. Правда, с пометкой «публикуется по запросу автора» и полным отказом об ответственности со стороны издания. Издатели не могли не видеть, что статья была полна ошибок. Во-первых, Гудвин не понимал, что задача заключается в построении равновеликого квадрата без измерительных приборов (линейка должна не иметь делений), а не в нахождении длины его стороны. Во-вторых, он утверждал, что площади круга и квадрата равны, если периметр последнего равен длине окружности, что, мягко говоря, неверно.
Так и не обнаружив в своих рассуждениях ошибок либо скрывая их, Эдвин Гудвин решил взять новую высоту. Он убедил Тейлора Рекорда, члена палаты представителей штата от своего родного округа Пози, выставить на рассмотрение Генеральной ассамблеи (аналог парламента) Индианы акт, который закреплял бы выводы Гудвина на законодательном уровне. Главный аргумент Гудвина заключался в том, что родная Индиана, благодаря его открытию, сможет сэкономить деньги. Ведь раз уж «правда» открылась, игнорировать её никто не сможет. А Гудвин собирался получать авторские отчисления за использование своего открытия (в первую очередь в учебных целях), но властям Индианы математический гений разрешил пользоваться его формулами бесплатно. Фермер и торговец лесом Тейлор Рекорд, проводивший свой первый и последний срок в качестве представителя, ничего не понял по математической части, но вскоре в палату представителей поступил Билль 246.
Этот билль выделялся множеством прекрасных деталей. Например, разделом 3, где говорилось, что гудвиновские решения проблем квадратуры круга, удвоения куба и трисекции угла (три неразрешимые классические задачи на построение) уже признаны вкладом в науку «Американским математическим ежемесячником». Как мы показали выше, это было неправдой.
Кроме того, нельзя пройти мимо фигуры, описанной в разделе 2:
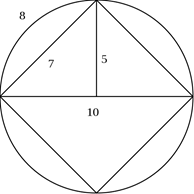
Это круг с длиной 32 и диаметром 10, в который вписан квадрат со стороной 7. Стороны изображённого квадрата, согласно теореме Пифагора, должны иметь длину:
что не равно 7. Тем не менее Гудвин делает отсюда вывод, что длина окружности и диаметр соотносятся как 4 к 5/4, то есть, 3,2 к 1. И хотя число пи в законопроекте не фигурирует, из него следует, что эта константа равна 3,2. Не 4, а именно 3,2.
18 января 1897 года Билль 246 был рассмотрен палатой представителей штата Индиана. Тематика законопроекта и обилие незнакомых греческих слов вызвали некоторое замешательство среди народных избранников. Сначала было предложено отправить акт на одобрение в финансовый комитет. Затем — в комитет по болотам, где тот «найдёт заслуженную могилу». В конце концов бумага оказалась в ведении комитета по образованию, который, как ни странно, отозвался о проекте положительно, в результате чего 6 февраля 1897 года последний был принят палатой представителей (распределение голосов 67:0). Итак, половина дела была сделана, оставалось убедить Сенат.
Но на беду Эдвина Гудвина, днём ранее в Индианаполис прибыл профессор Кларенс Уолдо — заведующий отделением математики престижного университета Пердью, которому было поручено пролоббировать бюджет Академии наук штата. Меньше всего он ожидал попасть на обсуждение математического закона. Уолдо показали копию законопроекта и предложили познакомить с его автором. Профессор отказался, заявив, что его знакомили с достаточным количеством сумасшедших. Более того, он провёл серьёзный разговор с сенаторами, объяснив им реальное положение дел с квадратурой круга.
В итоге, когда законопроект дошёл до Сената, он был встречен там прохладно. Рассматривавший заявку комитет по трезвости дал своё одобрение, однако 12 февраля 1897 года Сенат отложил принятие билля на неопределённый срок. Решающим стал аргумент одного из сенаторов о том, что Генеральная ассамблея не обладает полномочиями определять математическую истину. Не последнюю роль сыграла и кампания по высмеиванию закона, развёрнутая в прессе:
20 лет спустя профессор Уолдо предположил, что только вмешательство Академии наук предотвратило это чудовищное деяние. «Если это вывод верен, — добавил он, — то один только этот акт предотвращения стоил для Индианы, ревнивой к своей честной славе, больше, чем весь её прошлый и будущий вклад в публикацию протоколов заседаний Академии наук».
Врач и математик-любитель Эдвин Гудвин умер в 1902 году, всего лишь через пять лет после нашумевшего случая с законопроектом. Как было сказано в его некрологе, «он думал, что совершил великое открытие, и хотел принести этим пользу миру. Шли годы, и, когда он увидел, что детище его гения по-прежнему не принимается научным миром, его постигло разочарование, хотя он никогда не терял надежды и верил, что до конца своих дней увидит, как мир осознал величие его плана, и насладится минутой славы. Его чаяниям не суждено было сбыться, и в мирных интерьерах деревенской жизни разыгралась трагедия бесплодных амбиций».
Как видим, несмотря на все драматические события, развернувшиеся вокруг проблемы квадратуры круга, законодательный орган штата Индиана так окончательно и не принял решения относительно числа пи и подобный закон никогда не действовал и не действует.
В каком штате сша число пи равно 4
| [ | Tags | | | Забавно, Математика, Образование, США | ] |
Распространено мнение, что когда-то в штате Индиана законодательно устанавливалось число пи.
На самом деле истина довольно далека от такого описания.
Предлагавшийся закон широко известен под названием Indiana Pi Bill, однако в его тексте число пи не упоминается вообще.
В разделе 2 билля мы видим, какими Гудвин представляет параметры круга:
Furthermore, it has revealed the ratio of the chord and arc of ninety degrees, which is as seven to eight, and also the ratio of the diagonal and one side of a square which is as ten to seven.
То есть картинка в представлении Гудвина такова:
Отсюда можно получить и число пи (в оригинале определяется обратная величина):
. the fourth important fact, that the ratio of the diameter and circumference is as five-fourths to four.
Поскольку утверждается, что диаметр : (длина окружности) = 5/4 : 4, то отсюда пи = 4 : 5/4 = 3.2.
Гудвин попросил Тейлора Рекорда, представителя своего округа в Генеральной Ассамблее штата Индиана, представить этот закон. Рекорд был фермером и торговцем лесом, ничего не понимал в математике, но запрос выполнил. В Ассамблее тоже, похоже, очень мало кто понимал толком, о чем тут речь, а больше напиралось на денежную сторону.
Некий бывший учитель выступал так:
The case is perfectly simple. If we pass this bill which establishes a new and correct value of pi, the author offers our state without cost the use of his discovery and its free publication in our school textbooks, while everyone else must pay him a royalty.
В общем, нижняя палата закон приняла, и он добрался до Сената штата, но, надо думать, сенаторы все же были образованнее. К тому же повлияло мнение Кларенса Уолдо, профессора математики из университета Пердью, высмеявшего идею. В итоге в Сенате было выдвинуто предложение отложить рассмотрение на неопределенное время, и оно прошло. Больше этот закон в повестке никогда не появлялся.
В штате Индиана число ПИ по закону равно 4?
Какими бы не были смешными на наш взгляд некоторые законы в США, однако таковой к ним не относится. Это миф.
Действительно, более ста лет назад такой билль предлагался (Тейлором Рекордом, по просьбе математика-любителя Эдвина Гудвина), и даже прошел одобрение в нижней палате штата Индиана, однако в Сенате так и не был одобрен. Гудвин и Тейлор не смогли объяснить свою правоту и дать обоснование такому выводу профессору-математики Кларенсу Уолдо, который был приглашен на слушания по «Биллю Пи» в качестве эксперта. Поэтому этот билль так и не стал законом. Однако этот случай породил множество заблуждений, а штат Индиана прославился тем, что его теперь считают «штатом, где число пи равно 3,2» или «штатом, где число пи равно 4». Хотя это не соответствует действительности.
В Индиане как и везде, число «пи» подчиняется только законам математики и равняется 3,14.
Действительно, в ряде штатов США было закреплено на законодательном уровне то, что число Пи приравнивается (округляется) к 4, т.к. считать десятичные дроби для большинства граждан США является высшей математикой.
Причём, заметьте округлили до 4, а не до 3, что следовало бы по правилам округления в математике (число Пи=3,14). Но число 4 кратно 2, а значит счётные действия с ним проще.
Для нас это анекдотично, а для уровня образованности США норма.
Пространства с иным числом Пи
Недавно на Хабре в одной статье упомянули про вопрос «Что было бы с миром, если бы число Пи равнялось 4?» Я решил слегка поразмышлять на эту тему, используя некоторые (пусть и не самые обширные) знания в соответствующих областях математики. Кому интересно – прошу под кат.
Чтобы представить такой мир, нужно математически реализовать пространство с иным соотношением длины окружности к ее диаметру. Это я и попытался сделать.
Попытка №1.
Оговорим сразу, что рассматривать я буду только двумерные пространства. Почему? Потому что окружность, собственно, определена в двумерном пространстве (если рассмотреть размерность n>2, то отношение меры (n-1)-мерной окружности к ее радиусу даже не будет константой).
Так что для начала я попытался придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого я взял метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат (т.е. расстояние Чебышева). 
Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле. 
Да, в некоторой метрике это — окружность!
Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2. Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2. Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4. Получилось! Но нужно ли сильно радоваться? Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты. Вы можете представить себе мир, где по факту не определен поворот, и где окружностью является квадрат? Я пытался, честно, но у меня не хватило воображения.
Попытка №2.
Попытка №3.
Раз нам по-прежнему желательно наличие углов и поворотов, но евклидово пространство нас не устраивает, попробуем рассмотреть псевдоевклидово типа (1,1) (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками (а, как следствие, и скалярное произведение двух векторов) может быть отрицательным. Чтобы особо не мучиться, я взял метрику в которой скалярное произведение в декартовых координатах будет иметь вид 


Да-да! В определенном пространстве и это — окружность.
Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. После некоторых поисков информации в интернете, я пришел к выводу, что в псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.
Если кто-нибудь в комментариях расскажет мне, как формально считать длину кривой в псевдоевклидовом пространстве, я буду очень рад, ибо моих познаний в дифференциальной геометрии, топологии (а также усердного гугления) для этого не хватило.
Выводы:
Не знаю, можно ли писать о выводах после таких не сильно продолжительных исследований, но кое-что сказать можно. Во-первых, попытавшись представить пространство с иным числом Пи, я понял, что оно будет слишком абстрактно, чтобы быть моделью реального мира. Во-вторых, когда если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным. Если принять за данность возможность отрицательного квадрата расстояния (что для обычного человека — просто абсурд), то Пи не будет определено вовсе! Все это и наводит на мысль, что, возможно, мира с другим числом Пи и вовсе быть не могло? Ведь не зря же Вселенная именно такая, какая она есть. А может быть, это и реально, только обычной математики, физики и человеческого воображения для этого недостаточно. А вы как считаете?
Upd. Узнал точно. Длина кривой в псевдоевклидовом пространстве может быть определена только на каком-либо его евклидовом подпространстве. То есть, в частности, для получившейся в попытке N3 «окружности» вовсе не определено такое понятие как «длина». Соответственно, Пи там тоже посчитать нельзя.