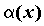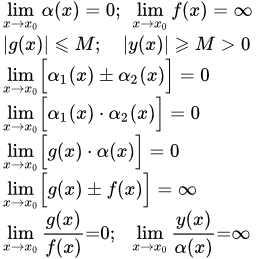в каком случае бесконечно малые и называются бесконечно малыми одного порядка в точке х0

В каком случае бесконечно малые и называются бесконечно малыми одного порядка в точке х0

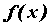
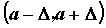
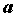
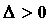
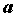
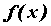
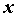
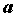
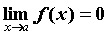
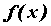
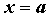
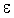
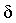
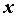
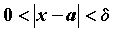
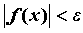
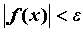
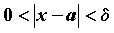
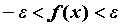
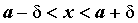
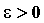
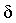
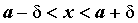
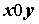
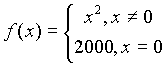
Рассмотрим функцию, определенную в некоторой окрестности точки , , за исключением, быть может, самой точки . Функция называется бесконечно малой при , стремящемся к , если . Если — бесконечно малая в точке , то для любого положительного числа , как бы мало оно ни было, существует такое положительное число , что для всех , удовлетворяющих неравенству , справедливо неравенство . Неравенства для всех , эквивалентные неравенствам , , означают, что для любого существует такое , что для график функции расположен на плоскости в прямоугольнике . Важно, что слова “за исключением, быть может, самой точки ” означают, что нас не интересует сама эта точка. Это можно понять, если рассмотреть функцию. При x, стремящемся к нулю, функция-таки стремится к нулю, независимо от того, какое значение она принимает в точке x=0. Следовательно, предел равен нулю и функция является бесконечно малой.

ПРИМЕР 1. Бесконечно малые функции

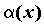
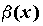
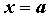
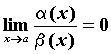
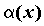
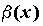
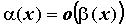
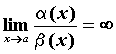
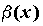
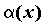
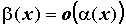
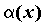
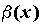
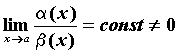
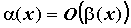
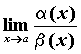
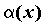
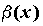
Пусть и — две функции, бесконечно малые в точке . Если , то говорят, что более высокого порядка малости, чем и обозначают . Если же , то более высокого порядка малости, чем ; обозначают . Бесконечно малые функции и называются бесконечно малыми одного порядка малости, если , обозначают . И, наконец, если не существует, то бесконечно малые функции и несравнимы.

ПРИМЕР 2. Сравнение бесконечно малых функций

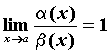
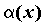
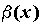
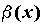
Если , то бесконечно малые функции и называются эквивалентными, обозначают

.

ПРИМЕР 3. Таблица эквивалентных бесконечно малых функций

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Вопрос 2. В каком случае бесконечно малые α (х) и β(х) называются бесконечно малыми одного порядка в точке х0?

ТягуновГеннадий Васильевич

Фетисов Иван Николаевич

Компьютерный набор Е.Е.Барышева

ИД № 06263 от 12.11.2001 г.

Подписано в печать Формат 60х84 1/16

Бумага писчая Плоская печать Усл. печ. л. 2,79

Уч.-изд. л. 2,3 Тираж 300 экз. Заказ

Редакционно-издательский отдел УГТУ-УПИ

620002, Екатеринбург, ул. Мира, 19

Ризография НИЧ УГТУ-УПИ

620002, Екатеринбург, ул. Мира, 19

Задание 1

Вопрос 1. Что называется функцией?

2. правило, по которому каждому значению аргумента х в соответствует одно и только одно значение функции у;

5. нет правильного ответа.

Вопрос 2. В каком случае можно определить обратную функцию?

1. когда каждый элемент имеет единственный прообраз;

2. когда функция постоянна;

3. когда функция не определена;

4. когда функция многозначна;

5. нет правильного ответа.

Вопрос 3. Какая функция называется ограниченной?

2. функция f(x) называется ограниченной, если m≤f(x)≤M;

4. функция f(x) называется ограниченной, если f(x)>0;

5. функция f(x) называется ограниченной, если f(x)≤0;

Вопрос 4. Какая точка называется предельной точкой множества А?

2. т.х₀ называется предельной точкой множества А, если в любой окрестности точки х₀ содержатся точки множества А, отличающиеся от х₀;

3. не принадлежащая множеству А;

4. нет правильного ответа;

5. лежащая на границе множества.

Вопрос 5. Может ли существовать предел в точке в том случае, если односторонние пределы не равны?

5. нет правильного ответа.

Задание 2

Вопрос 1. Является ли функция бесконечно малой при х→∞?

5. нет правильного ответа.

Вопрос 2. Является ли функция бесконечно большой при х→∞?

5. нет правильного ответа.

Вопрос 3. Является ли функция у=sin x бесконечно большой при х→∞?

5. нет правильного ответа.

Вопрос 4. Является ли функция у=cos x бесконечно большой при х→∞?

5. нет правильного ответа.

Вопрос 5. Является ли функция у=tg x бесконечно большой в т. х₀=0?

5. нет правильного ответа.

Задание 3

Вопрос 1. Является ли произведение бесконечно малой функции на функцию ограниченную, бесконечно малой функцией?

5. нет правильного ответа.

Вопрос 2. В каком случае бесконечно малые α (х) и β(х) называются бесконечно малыми одного порядка в точке х0?

2. если ;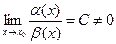

3. если ;

4. если их пределы равны 0;

5. нет правильного ответа.

Дата добавления: 2015-01-05 ; просмотров: 60 ; Нарушение авторских прав

Источник

MT1205: Математический анализ для экономистов

Бесконечно малые функции

Функцию %%f(x)%% называют бесконечно малой (б.м.) при %%x \to a \in \overline<\mathbb>%%, если при этом стремлении аргумента предел функции равен нулю.

Примеры

Отличное от нуля постоянное число, сколь бы оно ни было мало по абсолютному значению, не является б.м. функцией. Для постоянных чисел исключение составляет лишь нуль, поскольку функция %%f(x) \equiv 0%% имеет нулевой предел.

Теорема

Свойства бесконечно малых функций

По правилам предельного перехода при %%c_k = 1

\forall k = \overline<1, m>, m \in \mathbb%%, следуют утверждения:

Произведение б.м. функций при %%x \to a%% и функции, ограниченной в некоторой проколотой окрестности %%\stackrel<\circ><\text>(a)%% точки а, есть б.м. при %%x \to a%% функция.

Ясно, что произведение постоянной функции и б.м. при %%x \to a%% есть б.м. функция при %%x \to a%%.

Эквивалентные бесконечно малые функции

Бесконечно малые функции %%\alpha(x), \beta(x)%% при %%x \to a%% называются эквивалентными и пишутся %%\alpha(x) \sim \beta(x)%%, если

Теормема о замене б.м. функций эквивалентными

Эквивалентные б.м. функции.

Пусть %%\alpha(x)%% — б.м. функция при %%x \to a%%, тогда

Пример

Бесконечно большие функции

Функцию %%f(x)%% называют бесконечно большой (б.б.) при %%x \to a \in \overline<\mathbb>%%, если при этом стремлении аргумента функция имеет бесконечный предел.

Примеры

то говорят о положительной или отрицательной б.б. при %%a%% функции.

Пример

Функция %%1/%% — положительная б.б. при %%x \to 0%%.

Связь между б.б. и б.м. функциями

Если %%f(x)%% — б.б. при %%x \to a%% функция, то %%1/f(x)%% — б.м.

при %%x \to a%%. Если %%\alpha(x)%% — б.м. при %%x \to a%% функция, отличная от нуля в некоторой проколотой окрестности точки %%a%%, то при %%x \to a%%.

Свойства бесконечно больших функций

Приведем несколько свойств б.б. функций. Эти свойства непосредственно следуют из определения б.б. функции и свойств функций, имеющих конечные пределы, а также из теоремы о связи между б.б. и б.м. функциями.

Сумма ограниченной в некоторой проколотой окрестности точки %%a%% функции и б.б. функции при %%x \to a%% есть б.б. функция при %%x \to a%%.

Сумма двух б.б. функций при %%x \to a%% есть неопределенность. В зависимости от знака слагаемых характер изменения такой суммы может быть самым различным.

Пример

Источник

В каком случае бесконечно малые и называются бесконечно малыми одного порядка в точке х0

БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Можно доказать и обратную теорему.

Доказательство теоремы проведите самостоятельно.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

.

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,

Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример..

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c 2 ≠0.

Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.

Доказательство. Доказательство проведем методом от противного. Предположим, что b 3 – 6x 2 + 11x– 6, то при делении получим

II. Неопределенность .

При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.

При вычислении предела воспользовались равенством ,если x

Источник

Бесконечно малые и бесконечно большие функции

Определение бесконечно малой и бесконечно большой функции

Свойства бесконечно малых функций

Свойство суммы, разности и произведения бесконечно малых функций

Теорема о произведении ограниченной функции на бесконечно малую

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Свойства бесконечно больших функций

Теорема о сумме ограниченной функции и бесконечно большой

Теорема о произведении ограниченной снизу функции на бесконечно большую

Теорема о частном от деления ограниченной функции на бесконечно большую

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Свойство неравенств бесконечно больших функций

Это свойство имеет два частных случая.

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Арифметические свойства бесконечно больших и бесконечно малых функций

Приведенные выше свойства выполняются, если функция ограничена, а функция ограничена снизу по абсолютной величине положительным числом. При этом эти функции не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти функции будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых функций.

Доказательство свойств и теорем

Теорема о произведении ограниченной функции на бесконечно малую

Для доказательства этой теоремы, мы воспользуемся определением предела функции по Гейне. А также используем свойство бесконечно малых последовательностей, согласно которому произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Воспользуемся тем, что произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность:
.
Тогда, согласно определению предела последовательности по Гейне,
.

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Теорема о сумме ограниченной функции и бесконечно большой

Для доказательства теоремы, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью.

Поскольку сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о произведении ограниченной снизу функции на бесконечно большую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью.

Поскольку произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной функции на бесконечно большую

Для доказательства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью.

Поскольку частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью.

Поскольку частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Свойство неравенств бесконечно больших функций

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Источник