в каком случае четырехугольник можно вписать в окружность

Можно ли вписать четырёхугольник в окружность? Когда можно вписать?

Содержание:

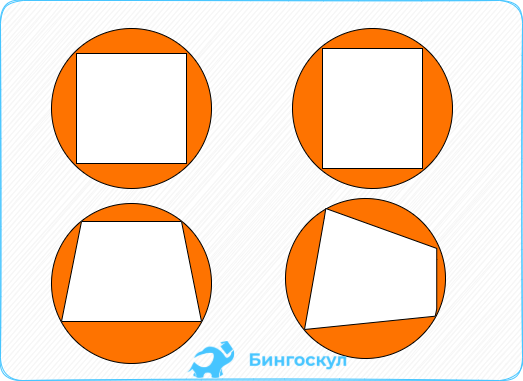
Почти в любой четырехугольник можно вписать окружность. Трапеция, прямоугольник и квадрат для этого подходят всегда, тогда как сложные геометрические фигуры с четырьмя углами вписываются в круг избирательно. Рассмотрим условия, при которых 4-угольник может касаться точек на окружности всеми вершинами.

Вписанный

Вписанной называется фигура, вершины которой располагаются на окружности. Все треугольники и правильные 4-угольники, вроде квадрата и прямоугольника, размещаются внутри круга, причём их вершины совмещаются с точками на окружности. Вокруг неправильной фигуры с четырьмя углами не всегда можно описать круг. Разбираемся, какие условия нужно выполнить для решения проблемы.

У квадрата и прямоугольника все углы прямые – равны 90°, но это не ключ к разгадке. Случай с параллелограммом тому подтверждение. Чем примечательны прямоугольные 4-угольники? Может дело в сумме углов?

Трапеция в круг вписывается, но только равнобедренная. Одно из её свойств – сумма внутренних углов равна 360°, а соседних – 180°. Получается, что четырехугольник можно вписать в окружность, если сумма противоположных углов равняется 180°. Проверим на практике.

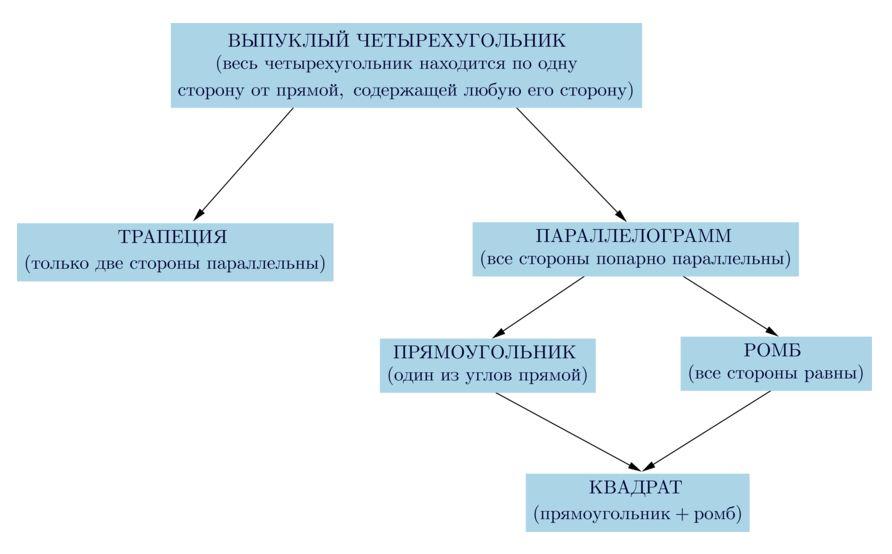
Помните: правило применимо только для выпуклых фигур, расположенных по одну сторону от проходящих через все стороны прямых.

Выпуклый дельтоид вписывается в круг, когда имеет пару прямых углов – называется прямоугольным.

Задача

Известны величины двух соседних углов вписанного четырёхугольника: 65° и 83°. Вычислить размеры сразу большего, затем – меньшего из оставшихся.

Известно, что сумма противоположных углов указанной геометрической фигуры равняется 180°. Отнимем от значения сначала большую цифру, затем – меньшую, чтобы выполнить условия задачи – найти неизвестные значения в указанном порядке.

180 – 65 = 115° – больший угол, 180 – 83 = 97° – меньший.

В какой четырехугольник можно вписать окружность

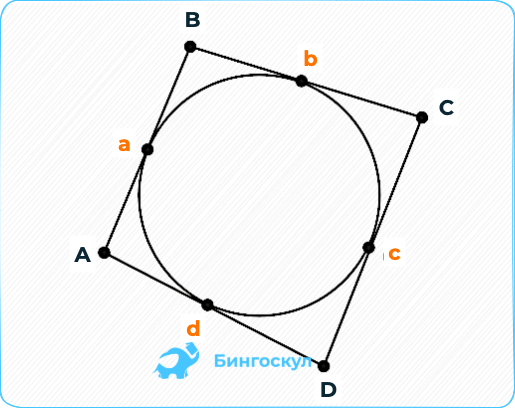
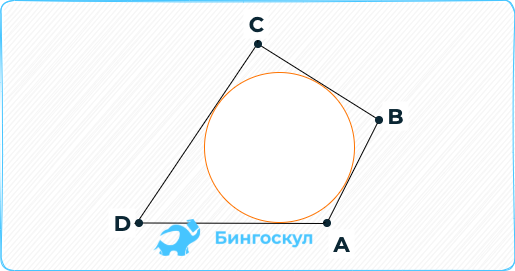
Описанным называют 4-угольник, стороны которого касаются круга. Существует теорема, показывающая, когда в четырехугольник можно вписать окружность: сумма его противоположных сторон должна быть одинаковой: AB + CD = BC + AD. В случае с прямоугольником условие не выполняется.

Правило работает для дельтоида, квадрата и даже неправильного выпуклого 4-угольника, подпадающего под теорему.

В параллелограмм вписывается круг в случае, если он является ромбом.

Задача

Стороны описанной фигуры относятся как 1:2:3. Найти длину четвёртой, если периметр равняется 32 см.

Составим уравнение. Зная, что суммы противоположных сторон 4-угольника равны:

Периметр равняется суме сторон: P = AB + ВС + AD + BC либо x + 2x + 2x + 3x = 32.

Источник

Многоугольник. Свойства четырехугольников вписанных в окружность.

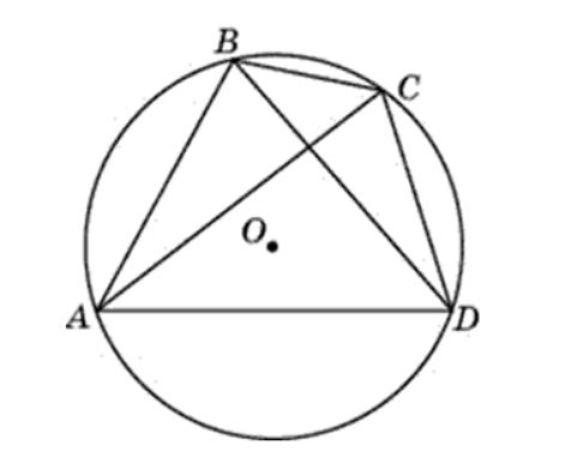
Если все вершины какого-нибудь многоугольника (ABCDE) лежат на окружности, то говорят, что этот многоугольник вписан в окружность, или что окружность описана около него.

Теорема.

В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым углам (2d).

Обратная теорема:

Если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым углам (2d), то около него можно описать окружность.

Необходимо обосновать, что около такого четырехугольника можно описать окружность. Через какие-нибудь три его вершины, например, A, B, С прочертим окружность (что всегда можно сделать).

Четвертая вершина D должна располагаться на этой окружности, потому что в противном случае угол D лежал бы своей вершиной или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги ABС, поэтому сумма B + D не измерялась бы полусуммой дуг ADС и ABС, т.е. сумма B + D не равнялась бы 2d, что противоречит условию.

Следствия.

1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобедренная.

Источник

Вписанный четырехугольник и его свойства (ЕГЭ 2022)

Мы видели, что вокруг всякого треугольника можно описать окружность. Вот так:

Вопрос: а можно ли получить вписанный четырехугольник?

Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?

Сейчас мы это выясним!

Вписанный четырехугольник — коротко о главном

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна \( \displaystyle 180<>^\circ \)

Если у четырехугольника есть два противоположных угла, сумма которых равна \( \displaystyle 180<>^\circ \), то такой четырехугольник вписанный.

Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна \( \displaystyle 180<>^\circ \).

\( \displaystyle \angle B+\angle D=180<>^\circ \).

Параллелограмм, вписанный в окружность – непременно прямоугольник, и центр окружности совпадает с точкой пересечения диагоналей.

Вписанный четырехугольник — определения и теоремы

Вот оказывается, что это неправда!

НЕ ВСЕГДА четырехугольник можно вписать в окружность.

Есть очень важное условие:

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна \( \displaystyle 180<>^\circ \).

На нашем рисунке: \( \displaystyle \alpha +\beta =180<>^\circ \)

Посмотри, углы \( \displaystyle \alpha \) и \( \displaystyle \beta \) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Они вроде бы тоже противоположные?

Можно ли вместо углов \( \displaystyle \alpha \) и \( \displaystyle \beta \) взять углы \( \displaystyle \varphi \) и \( \displaystyle \psi \)?

Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет \( \displaystyle 180<>^\circ \).

Оставшиеся два угла тогда сами собой тоже дадут в сумме \( \displaystyle 180<>^\circ \). Не веришь? Давай убедимся.

Пусть \( \displaystyle \alpha +\beta =180<>^\circ \). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, \( \displaystyle 360<>^\circ \).

То есть \( \displaystyle \alpha +\beta +\varphi +\psi =360<>^\circ \) — всегда! \( \displaystyle 180<>^\circ \)

Так что запомни крепко-накрепко:

Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна \( \displaystyle 180<>^\circ \)

Если у четырехугольника есть два противоположных угла, сумма которых равна \( \displaystyle 180<>^\circ \), то такой четырехугольник вписанный.

Доказательство смотри чуть дальше.

А пока давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна \( \displaystyle 180<>^\circ \).

Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма?

Вписанный параллелограмм

Попробуем сперва «методом научного тыка»:

Вот как-то не получается. Теперь применим знание:

Предположим, что нам как-то удалось посадить на параллелограмм \( \displaystyle ABCD\) окружность. Тогда непременно должно быть: \( \displaystyle \alpha +\beta =180<>^\circ \), то есть \( \displaystyle \angle B+\angle D=180<>^\circ \).

А теперь вспомним о свойствах параллелограмма: у всякого параллелограмма противоположные углы равны.

То есть \( \displaystyle \angle B = \angle D\).

У нас получилось, что

\( \displaystyle \left\< \begin\angle B=\angle D\\\angle B+\angle D=180<>^\circ \end \right.\) → \( \displaystyle \left\< \begin\angle B=90<>^\circ \\\angle D=90<>^\circ \end \right.\)

А что же углы \( \displaystyle A\) и \( \displaystyle C\)?

Ну, то же самое конечно.

\( \displaystyle ABCD\) – вписанный → \( \displaystyle \angle A+\angle C=180<>^\circ \) → \( \displaystyle \angle A=90<>^\circ \)

\( \displaystyle ABCD\) — параллелограмм→ \( \displaystyle \angle A=\angle C\) → \( \displaystyle \angle C=90<>^\circ \)

Источник

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырёхугольники и их свойства

Теорема 1 доказана.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник
Окружность, описанная около ромба
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, а p – полупериметр, т.е. Теорема Птолемея Докажем, что справедливо равенство: Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4). откуда вытекает равенство: (1) Источник Вписанный четырехугольник в окружность. Четырехугольник ABCD вписан в окружность С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы. Общие понятия Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки. Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры. Вам будет интересно: Железнодорожный техникум в Челябинске после 9 класса: специальности, отзывы Четырехугольник может быть следующих видов: Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º. Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника. Частные случаи Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи: Свойства вписанного четырехугольника в окружность Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример. Теорема 1 Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º. Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что Источник в соответствии с теоремой шеннона можно найти такой способ кодирования чтобы избыточность кода была → Вам также понравится в отличие часть речи какая 13.07.202219.07.2022 admin 0 как правильно подкормить помидоры калием сернокислым 20.07.202220.07.2022 admin 0 Модем или роутер в чем разница 22.07.202204.08.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев. Δ