в каком случае энтропия будет увеличиваться
Энтропия и ее изменение при различных процессах
Направленность химических реакций
В большинстве химических процессов одновременно происходит два явления: передача энергии и изменение в упорядоченном расположении частиц относительно друг друга. Все частицы (молекулы, атомы, ионы) стремятся к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой беспорядка (хаотичности, неупорядоченности) системы является энтропия S. Например, если баллон с газом соединить с пустым сосудом, то газ из баллона распределится по всему объему сосуда. Система из более упорядоченного состояния перейдет с менее упорядоченное, значит, энтропия при этом увеличится (ΔS > 0).
Энтропия всегда возрастает (ΔS > 0) при переходе системы из более упорядоченного состояния в менее упорядоченное: при переходе вещества из кристаллического состояния в жидкое и из жидкого в газообразное, при повышении температуры, при растворении и диссоциации кристаллического вещества и т.д.
При переходе системы из менее упорядоченного состояния в более упорядоченное энтропия системы уменьшается (ΔS 0 298, это справочная величина, измеряется в Дж/(К·моль) (Прил.2).
Например, стандартная энтропия
водяного пара…..S 0 298 = 188,72 Дж/(К·моль),
т.е. энтропия возрастает – степень беспорядка вещества в газообразном состоянии больше.
У графита S 0 298 = 5,74 Дж/(К·моль), у алмаза S 0 298 = 2,36 Дж/(К·моль), так как у веществ с аморфной структурой энтропия больше, чем с кристаллической.
Энтропия S 0 298, Дж/(К·моль) растет с усложнением молекул, например:
| вещество | O(г) | O2(г) | O3(г) |
| S 0 298 Дж/(К·моль) | 160,95 | 205,04 | 238,80 |
В ходе химических реакций энтропия также изменяется, так, при увеличении числа молекул газообразных веществ энтропия системы возрастает, при уменьшении - понижается.
Изменение энтропии системы в результате протекания процессов определяется по уравнению:
Например: в реакции
В левой части уравнения 1 моль газообразного вещества СО2(г), а в правой – 2 моль газообразного вещества 2СО(г), значит, объем системы увеличивается и энтропия возрастает (ΔS > 0).
С увеличением энтропии (ΔS > 0) протекают также реакции:
В реакции образования аммиака
Объем системы уменьшается, поэтому и энтропия понижается (ΔS 0 298 = 2,9 Дж/К
Пример №1.Рассчитайте и объясните изменение энтропии для процесса
Решение.Выпишем из Прил. 2 значения стандартных энтропий веществ
Согласно следствию из закона Гесса,
Согласно следствию из закона Гесса,
Энтропия незначительно увеличивается, это объясняется усложнением структуры молекулы SO2(г) по сравнению с молекулой O2(г).
Пример №3.Определить изменение энтропии для процесса:
Решение:Выпишем из Прил. 2 значения стандартных энтропий
ΔS 0 = S 0 СО2(г) – (S 0 С(г) + S 0 О2(г)) = 213,68 – (5,74+ 205,04) = 2,9 Дж/К.
Так как ΔS > 0, энтропия в процессе реакции незначительно увеличивается. Объем системы не изменяется, но энтропия растет вследствие усложнения структуры молекулы СО2 по сравнению с молекулой О2.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
# чтиво | Энтропия растет с течением времени или создает его?
Вопрос будет следующим:
«Допустим, энтропия — это мера беспорядка объектов. Но что в ней такого важного, что она должна быть законом?».
Если вы посмотрите почти на все законы физики, время будет течь почти с опозданием. Сделайте фильм из столкновения двух электронов, а потом запустите фильм в обратном порядке, и вторая версия будет выглядеть так же нормально и физически достоверно, как и первый вариант. На микроскопическом уровне время кажется практически симметричным. Потому что, как мы писали, на этом уровне не работает привычная нам термодинамика.
На макроскопическом уровне все совершенно иначе. Вы не помните будущее, например, не можете склеить яйцо или разделить коктейль на составляющие. И говоря о возможности путешествий во времени, мы подразумеваем только одну стрелу времени, один вектор, одно направление: вперед.
Есть один общий знаменатель, отличающий будущее от прошлого: все запутывается. Вы знаете это как «второй закон термодинамики». Или не знаете. Мне все равно.
Второй закон гласит, буквально, что все разваливается, или что вещи становятся все более и более хаотичными и беспорядочными со временем, но это не совсем так. Правильно так: полная энтропия замкнутой системы возрастает со временем. Энтропия является мерой числа способов, которыми вы можете переворачивать вещи с ног на голову и сохранять все макроскопические величины неизменными.
Весьма школьный пример
В любой момент времени вы будете видеть случайный снимок трех молекул. Есть восемь разных путей организовать молекулы, но только два из них (ЛЛЛ, ППП) разместят все три молекулы в одной части контейнера. Это всего лишь 25 % вероятности. В остальное время атомы, скорее всего, будут распределены равномерно. И равномерное распределение — это более высокое состояние энтропии, чем концентрированное.
Вы можете играть в эту же игру, набрав полную ладонь монет и подбрасывая их в воздух. Орел и решка — это правая и левая часть коробки, и наоборот. Проделайте этот жест несколько раз и увидите, что молекулы почти всегда равномерно распределяются.
Большие числа превращают вероятность в закон
Если вы увеличите число молекул воздуха, к примеру, до 10 26 или выше, вероятность подсказывает, что случайные движения в итоге распределят молекулы «равномерно». Благодаря квантовой механике, случайность становится принципиальной составляющей всего этого. То есть, поскольку есть техническая вероятность того, что все молекулы воздуха внезапно покинут вашу спальню, пока вы спите, за несколько минут, это явно не то, чего стоит бояться ночью.
Растущая энтропия — на самом деле закон, поскольку во Вселенной так много частиц, что вероятность того, что все они спонтанно выстроятся в состояние низкой энтропии, ошеломляюще мала. Этот же тип случайно работает в отношении азартных игр и прогнозирования погоды.
Ну или еще пример. Вам выпадает решка два раза подряд, и вы совсем не удивляетесь этому. Но если кому-то решка выпадает сто раз кряду, это становится подозрительным. Чтобы оценить масштаб такого события, представьте себе: если вы будете подбрасывать монетку 10 раз в секунду, у вас уйдет времени в триллион раз больше нынешнего возраста вселенной, прежде чем вы дождетесь результата. Грубо говоря, в определенный момент система становится настолько большой, что шанс на то, что энтропия будет уменьшаться, не просто мал, но крайне близок к нулю. Поэтому мы называем это «вторым законом».
Креационисты среди вас могут использовать это как доказательство, что сложные вещи (вроде людей или динозавров) никогда не смогли бы сформироваться. В конце концов, вы ведь высоко упорядоченный человек, стоит полагать. Если вы облако газа, примите мои извинения. Но если предположить, что вы человек, нет ничего странного в том, что вы существуете как маленький шанс высокого порядка.
Суть правила в том, что энтропия растет во всей вселенной. Например, если вы сделаете хорошенький холодильник, полный холодного воздуха, вы сделаете это за счет высокой энтропии горячего воздуха. Вот почему кондиционер нуждается в выхлопе, а обогреватель — нет. По этой же причине вы не можете построить вечный двигатель. Часть энергии всегда будет преобразовываться в тепло.
Энтропия непрерывно увеличивается со временем. Вы сидите в горячей ванне в прохладной комнате, чувствуете себя тепло и уютно, но потом события начинают принимать угрожающий поворот: вода в номере по температуре приближается к воздуху, вам становится холодно, вас атакуют мурашки.
То же самое касается будущего Вселенной. С течением времени тепло равномерно распределится во Вселенной. Звезды выгорят, черные дыры испарятся, станет темно и холодно. Бум.
Время и второй закон
Одной из причин, почему вообще эти идеи набирают обороты, является загадка наблюдателя. Юная вселенная, судя по всему, находилась в состоянии высокого порядка, но нет никаких фундаментальных причин, почему это должно быть так. Вселенная, созданная сразу после Большого Взрыва, должна была бы находиться в состоянии полного хаоса, но вместо этого она была невероятно упорядоченной. Гравитационная система высокой энтропии свернулась в комки (произведя звезды, галактики и черные дыры), но вселенная была гладкой. Почему?
Другие заходят еще дальше. Эрик Верлинде, например, утверждает, что такие явления, как гравитация, вытекают из второго закона термодинамики (и теории струн). Стоит отметить, что интересных идей много. Многие говорят, что время заставляет энтропию расти, но не энтропия порождает время. Для кого-то энтропия это просто то, что происходит.
Или должно произойти с высокой вероятностью.
Изменение энтропии
Вы будете перенаправлены на Автор24
Энтропия – это фундаментальная физическая величина. Введение этого понятия завершило этап становления понятийного аппарата термодинамики. Следующим этапом развития этой науки было выяснение физического смысла энтропии.
Установление принципа Больцмана (формулы Больцмана) и таким образом связи между термодинамикой и статистической физикой, позволило энтропии покинуть пределы физики и войти в другие области знаний.
Энтропия – это общезначимое понятие, применяемое во множестве наук, например, в:
Введено это понятие было Р. Клаузиусом. Важные работы посвятил энтропии Л. Больцман, М. Планк.
Функция состояния полным дифференциалом которой является δQ/T называется энтропией ($S$):
Отметим, что формула (1) справедлива только для обратимых процессов. Например, для процессов, проводимых в идеальном газе.
Важно, что выражение (1) определяет не саму энтропию, а ее изменение, или разность энтропий. При помощи данной формулы можно вычислить, каково изменение энтропии, если термодинамическая система переходит из одного состояния в другое, но нельзя понять, какова энтропия каждого из этих состояний.
Напомним формулу Больцмана для энтропии, так как она нам поможет понять физический смысл, процессов, которые происходят с энтропией:
$S=klnW\, \left( 2 \right)$
Изменение энтропии, исходя из статистической формулы Больцмана, найдем как:
Готовые работы на аналогичную тему
Вычисление изменения энтропии в изотермическом процессе
Вычислим изменение энтропии в одном моле идеального газа при изотермическом процессе ($T=const$). Оттолкнемся от первого начала термодинамики в дифференциальной форме:
$\delta Q=dU+pdV\, \left( 3 \right)$,
Найдем отношение всех слагаемых выражения (3) и температуры:
Для идеального газа справедливо уравнение Менделеева – Клапейрона, учитывая, что у нас 1 моль газа:
$\frac
в этом случае мы можем записать для уравнения (4):
$\frac<\delta Q>
По определению (1), и принимая во внимание (7), запишем:
$dS=d\left( C_
Формула (8) показывает нам, что в изотермическом процессе изменяется только второе слагаемое правой части:
Данный результат очевиден, так как если увеличивается объем, то возрастает количество мест, которое смогут занять частицы при неизменяющемся их количестве. Следовательно, растет число разных возможностей расположения на этих местах (увеличивается количество пространственных микросостояний). Увеличение числа микросостояний означает увеличение энтропии (см формулу (2)).
Изменение энтропии в изохорическом процессе
$dS=d\left( C_
После интегрирования (9), получим:
Формула (10) показывает, что в изохорическом процессе при увеличении температуры происходит рост энтропии. Данный результат можно пояснить так:
Изменение энтропии в адиабатном процессе
Адиабатный процесс характеризуется тем, что он происходит без теплообмена (δQ=0). Исследуя адиабатный процесс в идеальном газе, за основу для вычисления энтропии примем выражение (8). Найдем интеграл правой и левой частей этого выражения, получим:
Преобразуем выражение (11), приняв во внимание формулу (13):
Вспомним соотношение Майера:
и сделаем вывод о том, что изменение энтропии в адиабатном процессе нет:
Адиабатный процесс является изоэнтропийным ($S=const$).
При адиабатном расширении газа увеличение энтропии может идти только за счет увеличения объема, но при этом происходит уменьшение температуры, и энтропия уменьшается из-за уменьшения температуры. Данные тенденции взаимно компенсируют друг друга.
Рисунок 1. Изменение энтропии в адиабатном процессе. Автор24 — интернет-биржа студенческих работ
$\Delta S_<1>=\int\limits_a^b \frac
\ln \left(\frac
Изменение энтропии второго газа запишем аналогично:
$\Delta S_<2>=\nu c_
\ln \left( \frac
Поскольку энтропия является аддитивной величиной, то полное изменение энтропии найдем как сумму:
Вездесущая энтропия: от смерти Вселенной до груды грязной посуды
Михаил Петров
«Все процессы в мире происходят с увеличением энтропии» — эта расхожая формулировка превратила энтропию из научного термина в непреложное свидетельство обреченной борьбы человека с окружающим его беспорядком. Но что в оригинале скрывается за этой физической величиной? И как можно посчитать энтропию? «Теории и практики» попытались разобраться в этом вопросе и найти спасение от надвигающегося распада.
Термодинамика и «тепловая смерть»
Впервые термин «энтропия» в 1865 году ввел немецкий физик Рудольф Клаузиус. Тогда он имел узкое значение и использовался в качестве одной из величин для описания состояния термодинамических систем — то есть, физических систем, состоящих из большого количества частиц и способных обмениваться энергией и веществом с окружающей средой. Проблема заключалась в том, что до конца сформулировать, что именно характеризует энтропия, ученый не смог. К тому же, по предложенной им формуле можно было определить только изменение энтропии, а не ее абсолютное значение.
Упрощенно эту формулу можно записать как dS = dQ/T. Это означает, что разница в энтропии двух состояний термодинамической системы (dS) равна отношению количества тепла, затраченного на то, чтобы изменить первоначальное состояние (dQ), к температуре, при которой проходит изменение состояния (T). Например, чтобы растопить лед, нам требуется отдать ему некоторое количество тепла. Чтобы узнать, как изменилась энтропия в процессе таяния, нам нужно будет поделить это количество тепла (оно будет зависеть от массы льда) на температуру плавления (0 градусов по Цельсию = 273, 15 градусов по Кельвину. Отсчет идет от абсолютного нуля по Кельвину ( — 273° С ), поскольку при этой температуре энтропия любого вещества равна нулю). Так как обе величины положительны, при подсчете мы увидим, что энтропии стало больше. А если провести обратную операцию — заморозить воду (то есть, забрать у нее тепло), величина dQ будет отрицательной, а значит, и энтропии станет меньше.
Примерно в одно время с этой формулой появилась и формулировка второго закона термодинамики: «Энтропия изолированной системы не может уменьшаться». Выглядит похоже на популярную фразу, упомянутую в начале текста, но с двумя важными отличиями. Во-первых, вместо абстрактного «мира» используется понятие «изолированная система». Изолированной считается та система, которая не обменивается с окружающей средой ни веществом, ни энергией. Во-вторых, категорическое «увеличение» меняется на осторожное «не убывает» (для обратимых процессов в изолированной системе энтропия сохраняется неизменной, а для необратимых — возрастает).
За этими скучноватыми нюансами скрывается главное: второй закон термодинамики нельзя без оглядки применять ко всем явлениям и процессам нашего мира. Хороший тому пример привел сам Клаузиус: он считал, что энтропия Вселенной постоянно растет, а потому когда-нибудь неизбежно достигнет своего максимума — «тепловой смерти». Этакой физической нирваны, в которой не протекают уже никакие процессы. Клаузиус придерживался этой пессимистической гипотезы до самой смерти в 1888 году — на тот момент научные данные не позволяли ее опровергнуть. Но в 1920-х гг. американский астроном Эдвин Хаббл доказал, что Вселенная расширяется, а значит, ее
сложно назвать изолированной термодинамической системой. Поэтому современные физики к мрачным прогнозам Клаузиуса относятся вполне спокойно.
Энтропия как мера хаоса
Поскольку Клаузиус так и не смог сформулировать физический смысл энтропии, она оставалась абстрактным понятием до 1872 года — пока австрийский физик Людвиг Больцман не вывел новую формулу, позволяющий рассчитывать ее абсолютное значение. Она выглядит как S = k * ln W (где, S — энтропия, k — константа Больцмана, имеющая неизменное значение, W — статистический вес состояния). Благодаря этой формуле энтропия стала пониматься как мера упорядоченности системы.
Как это получилось? Статистический вес состояния — это число способов, которыми можно его реализовать. Представьте рабочий стол своего компьютера. Сколькими способами на нем можно навести относительный порядок? А полный беспорядок? Получается, что статистический вес «хаотичных» состояний гораздо больше, а, значит больше и их энтропия. Посмотреть подробный пример и рассчитать энтропию собственного рабочего стола можно здесь.
В этом контексте новый смысл приобретает второй закон термодинамики: теперь процессы не могут самопроизвольно протекать в сторону увеличения порядка. Но и тут не стоит забывать про ограничения закона.
Иначе человечество уже давно было бы в рабстве у одноразовой посуды. Ведь каждый раз, когда мы моем тарелку или кружку, нам на помощь приходит простейшая самоорганизация. В составе всех моющих средств есть поверхно-активные вещества (ПАВ). Их молекулы составлены из двух частей: первая по своей природе стремится к контакту с водой, а другая его избегает.
При попадании в воду молекулы «Фэйри» самопроизвольно собираются в «шарики», которые обволакивают частички жира или грязи (внешняя поверхность шарика это те самые склонные к контакту с водой части ПАВ, а внутренняя, наросшая вокруг ядра из частички грязи — это части, которые контакта с водой избегают). Казалось бы, этот простой пример противоречит второму закону термодинамики. Бульон из разнообразных молекул самопроизвольно перешел в некое более упорядоченное состояние с меньшей энтропией. Разгадка снова проста: систему «Вода-грязная посуда после вечеринки», в которую посторонняя рука капнула моющего средства, сложно считать изолированной.
Черные дыры и живые существа
Со времен появления формулы Больцмана термин «энтропия» проник практически во
все области науки и оброс новыми парадоксами. Возьмем, к примеру астрофизику и пару «черная дыра — падающее в нее тело». Ее вполне можно считать изолированной системой, а значит, ее энтропия такой системы должна сохраняться. Но она бесследно исчезает в черной дыре — ведь оттуда не вырваться ни материи, ни излучению. Что же происходит с ней внутри черной дыры?
Некоторые специалисты теории струн утверждают, что эта энтропия превращается в энтропию черной дыры, которая представляет собой единую структуру, связанную из многих квантовых струн (это гипотетические физические объекты, крошечные многомерные структуры, колебания которых порождают все элементарные частицы, поля и прочую привычную физику). Впрочем, другие ученые предлагают менее экстравагантный ответ: пропавшая информация, все-таки возвращается в мир вместе с излучением, исходящим от черных дыр.
Еще один парадокс, идущий вразрез со вторым началом термодинамики — это существование и функционирование живых существ. Ведь даже живая клетка со всеми ее биослоями мембран, молекулами ДНК и уникальными белками — это высокоупорядоченная структура, не говоря уже о целом организме. За счет чего существует система с такой низкой энтропией?
Точнее организм питается углеводами, белками и жирами. Высокоупорядоченными, часто длинными молекулами со сравнительно низкой энтропией. А взамен выделяет в окружающую среду уже гораздо более простые вещества с большей энтропией. Вот такое вечное противостояние с хаосом мира.
Энтропия? Это просто!
Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora
Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
Так что же такое энтропия?
Энтропия — это то, как много информации вам не известно о системе
Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации. 
Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём). 
Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).
А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.
Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.
Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:
Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B. 
Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.
Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.
Физический пример: газ под поршнем
Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях. 
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:
Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.
Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.
Твёрдые тела и потенциальная энергия
Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия. 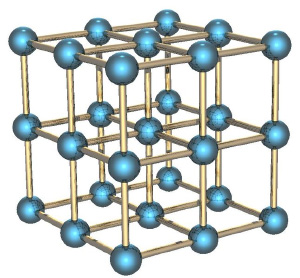
Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.
Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.
Понимаем второй закон термодинамики
Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад. 
Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.
Перемешивание газов
И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.
Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).
Разбираемся с демоном Максвелла
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа. 
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?
Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.
Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.


