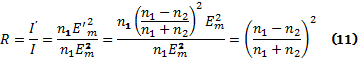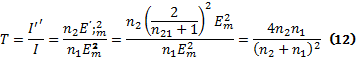в каком случае фаза колебаний волны меняется на противоположную при отражении

Изменение фазы волны при ее отражении

4. Изменение фазы волны при ее отражении.

Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на радиан соответствует появлению дополнительного хода луча, равного .

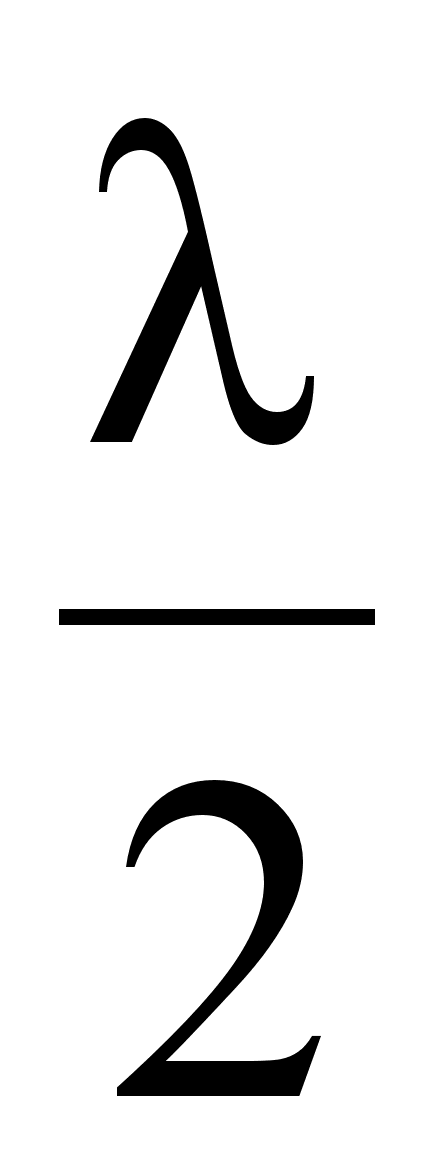
Глава 2. Звуковые волны.

1.Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.

Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.

2. Избыточное звуковое давление. Уравнение звуковой волны.

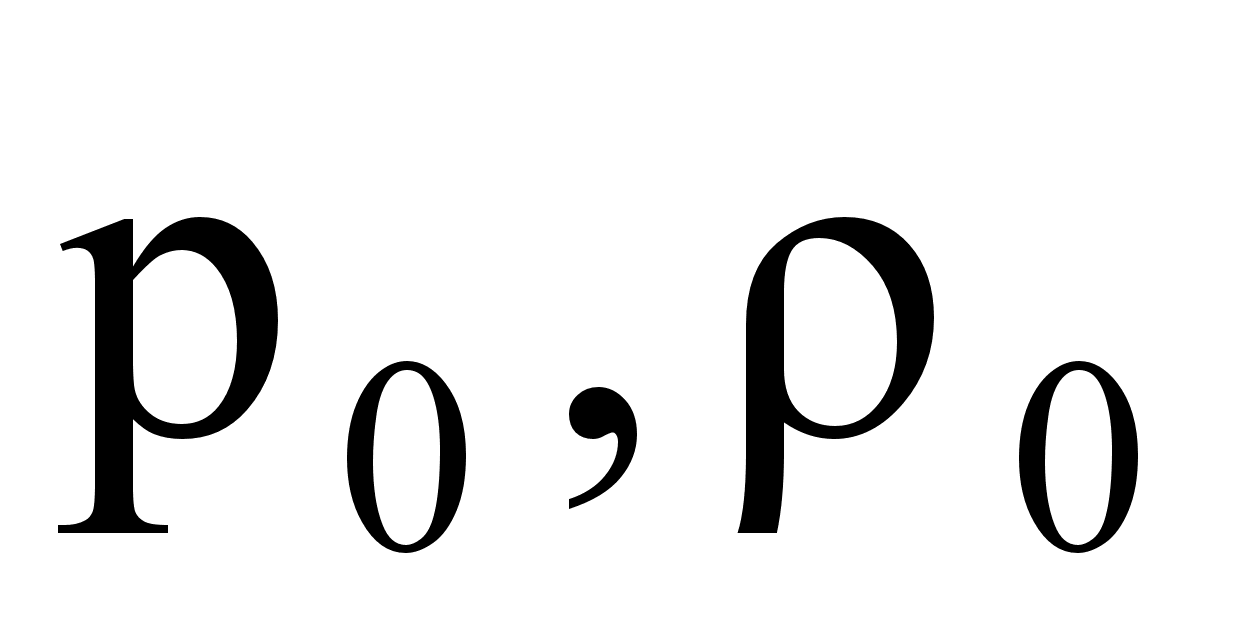
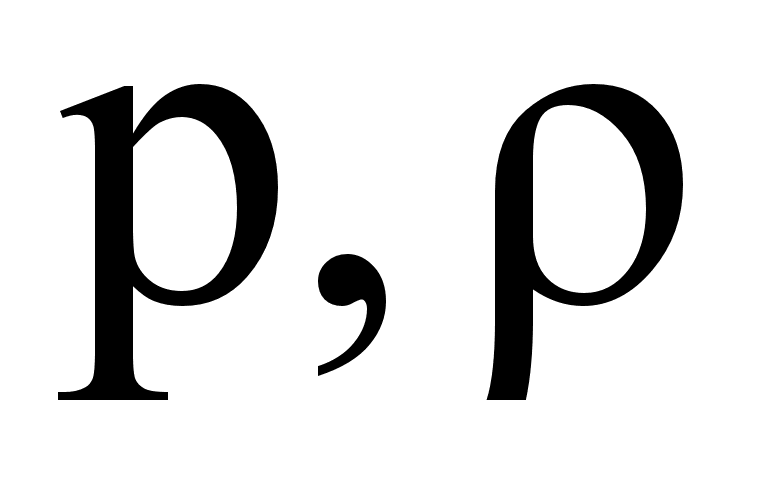
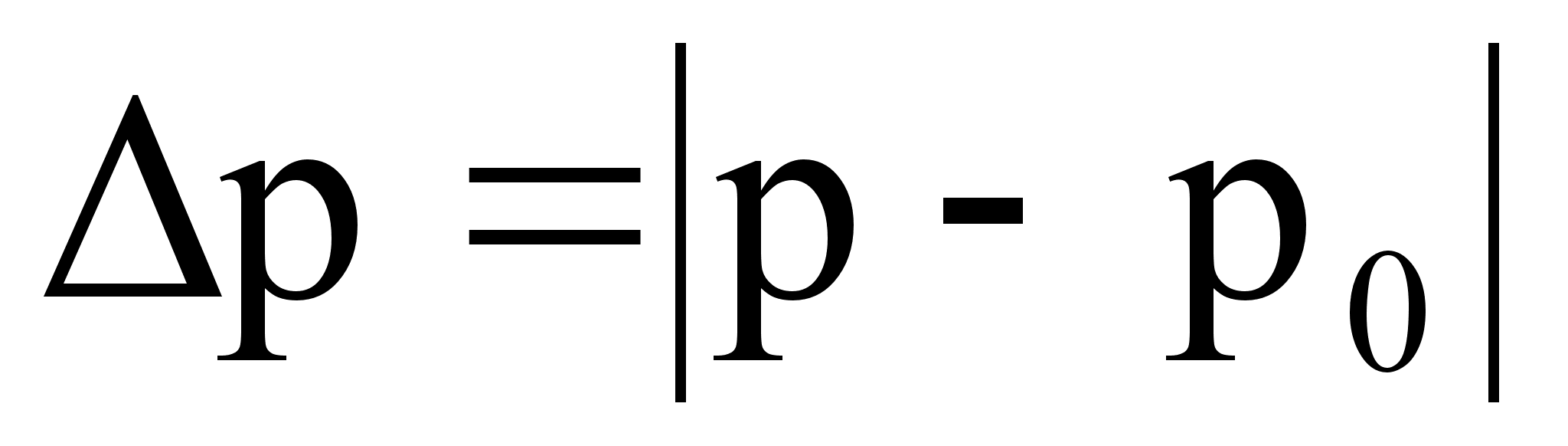
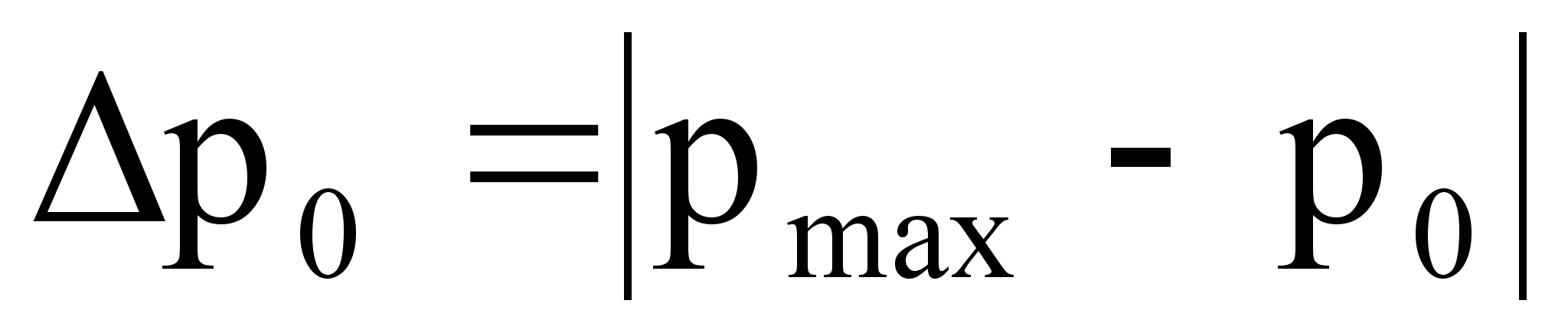
Если — давление и плотность невозмущенной среды (среды, по которой не проходит волна), а — давление и плотность среды при распространении в ней волнового процесса, то величина называется избыточным давлением. Величина есть максимальное значение избыточное давление (амплитуда избыточного давления).

Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:

,

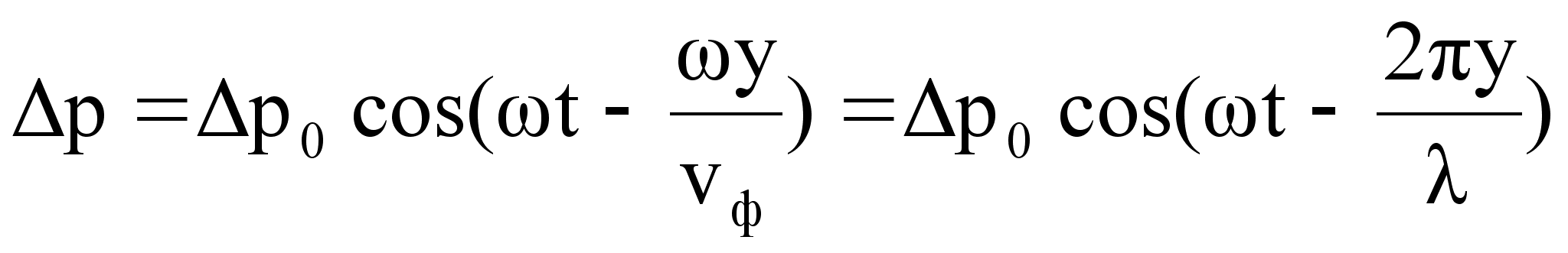
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.

Если ввести величину избыточной плотности и ее амплитуды так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так:

.

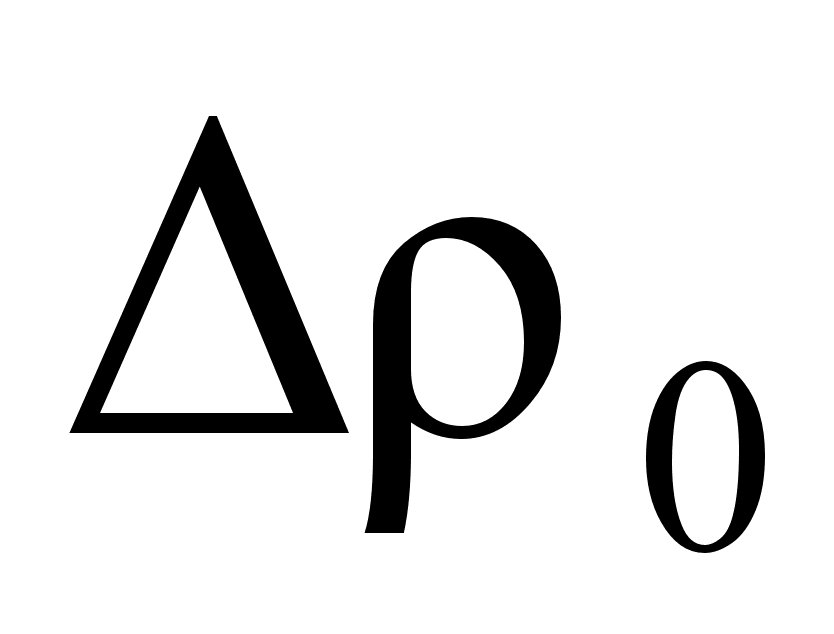
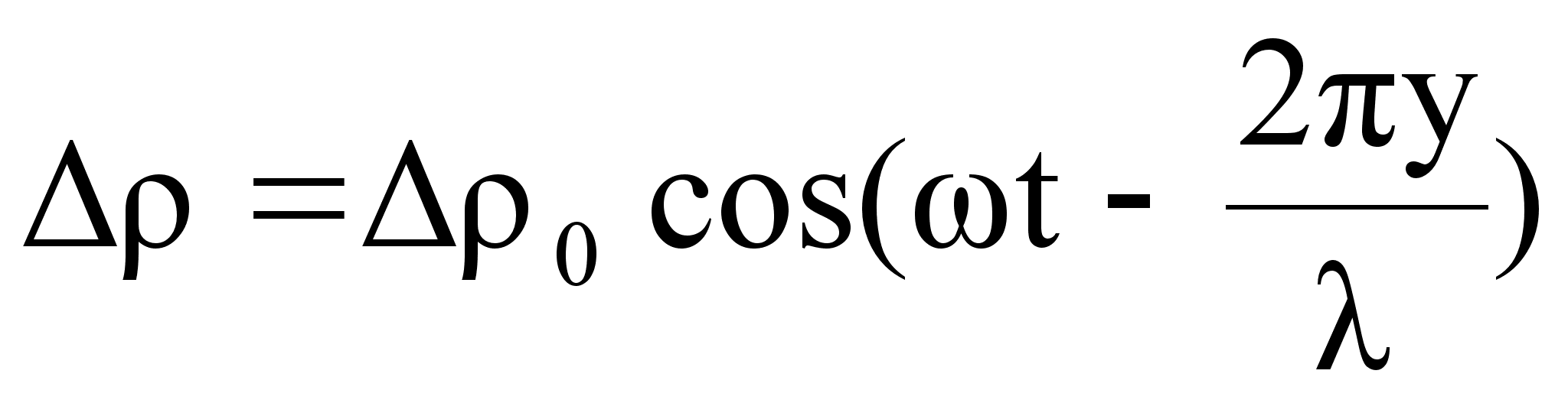
3. Объективные и субъективные характеристики звука.

Само слово «звук» отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.

К объективным (физическим ) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.

Высота звука определяется частотой

Тембр (окраска звука)Тембр звука определяется его спектромГромкость (сила звука)Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды)

Остановимся на некоторых определениях.

Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.

Интенсивᘀность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).

Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.

Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.

Источник

Потеря половины длины волны

нагуглил ответ на свой последний вопрос тут
http://www.physbook.ru/ind…

цитата оттуда:
«При отражении луча от среды с меньшим показателем преломления фаза колебаний волны не меняется. При отражении луча от среды с большим показателем преломления, волна меняет фазу колебаний на противоположную (на π), что равносильно потере полуволны (λ/2). «

В соответствии с формулами Френеля на границе раздела двух сред преломленная световая волна всегда в фазе с падающей волной, отраженная волна — либо в фазе, либо в противофазе.

Иной сдвиг фазы отраженной волны возникает только в случае полного внутреннего отражения.

Проанализируйте формулы Френеля, анализ даст ответ на Ваш вопрос))

Задайте свой вопрос по физике
профессионалам

Другие вопросы на эту тему:

Задача по оптике

луч света падает на границу раздела двух сред под углом 32 градуса абсолютный показатель преломления первой среды равен 2,4. каков абсолютный показатель преломления второй среды если известно что преломленный луч перпендикулярен отраженному?

если можно с решением

Толщина пленки

Помогите пожалуйста с задачкой по оптике

Интерференция света

Задача:
«Лучи белого света падают под углом alpha = 60гр на очень тонкую прозрачную пластинку. При этом пластинка в отраженном свете кажется зеленой. Как изменится цвет пластинки, при небольшом уменьшении угла падения лучей? При его увеличение?»

решение:
http://s1.ipicture.ru/uploa….png
честно говоря я уже совсем запарился — не могу себе…

Помогите решить 2 задачи по физике

1) На стеклянную пластинку положена выпуклой сторой плоско-выпуклая линза. Сверхулинза освещена монохроматически светом длиной волны 5*10^-7 м. Найти радиус кривизны линзы, если радиус четвертого тёмного кольца Ньютона в отраженном свете равен 2 мм.

2)На поверхность дифракционной решетки нормально падает монохроматический свет. постоянная дифракционной решетки в 4,6 раза больше длины световой волны. Найти общее число дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.

Источник

В каком случае фаза колебаний волны меняется на противоположную при отражении

Необходимы более веские доказательства того, что свет при распространении ведет себя как волна. Любому волновому движению присущи явления интерференции и дифракции. Для того чтобы быть уверенным в том, что свет имеет волновую природу, необходимо найти экспериментальные доказательства интерференции и дифракции света.

Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?

Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.

Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.

Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.

Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d₁ и d₂, волны имеют разность хода Δd = d₂—d₁. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:

Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.

Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:

Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.

Источники, удовлетворяющие этим условиям, называются когерентными. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.

Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться. Поэтому амплитуда результирующих колебаний с течением времени изменяется. В результате максимумы и минимумы перемещаются в пространстве и интерференционная картина размывается.

Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы и в минимумах интерференционной картины выделяется тепло? Ничего подобного. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает совсем.

ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН

Если свет представляет собой поток волн, то должно наблюдаться явление интерференции света. Однако получить интерференционную картину (чередование максимумов и минимумов освещенности) с помощью двух независимых источников света, например двух электрических лампочек, невозможно. Включение еще одной лампочки лишь увеличивает освещенность поверхности, но не создает чередования минимумов и максимумов освещенности.

Выясним, в чем причина этого и при каких условиях можно наблюдать интерференцию света.

Условие когерентности световых волн. Причина состоит в том, что световые волны, излучаемые различными источниками, не согласованы друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковые длины волн и постоянную разность фаз в любой точке пространства. Напомним, что такие согласованные волны с одинаковыми длинами волн и постоянной разностью фаз называются когерентными.

Почти точного равенства длин волн от двух источников добиться нетрудно. Для этого достаточно использовать хорошие светофильтры, пропускающие свет в очень узком интервале длин волн. Но невозможно осуществить Постоянство разности фаз от двух независимых источников. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн, имеющими длину около метра. И такие цуги волн от обоих источников налагаются друг на друга. В результате амплитуда колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги волн от различных источников сдвинуты друг относительно друга по фазе. Волны от различных источников света некогерентны из-за того, что разность фаз волн не остается постоянной. Никакой устойчивой картины с определенным распределением максимумов и минимумов освещенности в пространстве не наблюдается.

Интерференция в тонких пленках. Тем не менее интерференцию света удается наблюдать. Курьез состоит в том, что ее наблюдали очень давно, но только не отдавали себе в этом отчета.

Вы тоже много раз видели интерференционную картину, когда в детстве развлекались пусканием мыльных пузырей или наблюдали за радужным переливом цветов тонкой пленки керосина или нефти на поверхности воды. «Мыльный пузырь, витая в воздухе. зажигается всеми оттенками цветов, присущими окружающим предметам. Мыльный пузырь, пожалуй, самое изысканное чудо природы» (Марк Твен). Именно интерференция света делает мыльный пузырь столь достойным восхищения.

Английский ученый Томас Юнг первым пришел к гениальной мысли о возможности объяснения цветов тонких пленок сложением волн 1 и 2 (рис. 123), одна из которых (1) отражается от наружной поверхности пленки, а вторая (2) —от внутренней. При этом происходит интерференция световых волн — сложение двух волн, вследствие которого наблюдается устойчивая во времени картина усиления или ослабления результирующих световых колебаний в различных точках пространства. Результат интерференции (усиление или ослабление результирующих колебаний) зависит от угла падения света на пленку, ее толщины и длины волны. Усиление света произойдет в том случае, если преломленная волна 2 отстанет от отраженной волны 1 на целое число длин волн. Если же вторая волна отстанет от первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света.

Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, обеспечивается тем, что они являются частями одного и того же светового пучка. Цуг волн от каждого излучающего атома разделяется пленкой на два, а затем эти части сводятся вместе и интерферируют.

Юнг также понял, что различие в цвете связано с различием в длине волны (или частоте световых волн). Световым пучкам различного цвета соответствуют волны различной длины. Для взаимного усиления волн, отличающихся друг от друга длиной (углы падения предполагаются одинаковыми), требуется различная толщина пленки. Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом должны появиться различные цвета.

Кольца Ньютона. Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу (рис. 124). Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив радиусы колец, можно вычислить длины волн.

Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.

При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.

Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в n раз. Так как v = λv, то при этом должна уменьшиться в n раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в n раз именно длина волны, а не частота.

Интерференция электромагнитных волн. На опытах с генератором СВЧ можно наблюдать интерференцию электромагнитных (радио) волн.

Генератор и приемник располагают друг против друга (рис. 125). Затем подводят снизу металлическую пластину в горизонтальном положении. Постепенно поднимая пластину, обнаруживают поочередное ослабление и усиление звука.

Явление объясняется следующим образом. Часть волны из рупора генератора непосредственно попадает в приемный рупор. Другая же ее часть отражается от металлической пластины. Меняя расположение пластины, мы изменяем разность хода прямой и отраженной волн. Вследствие этого волны либо усиливают, либо ослабляют друг друга в зависимости от того, равна ли разность хода целому числу длин волн или нечетному числу полуволн.

Источник

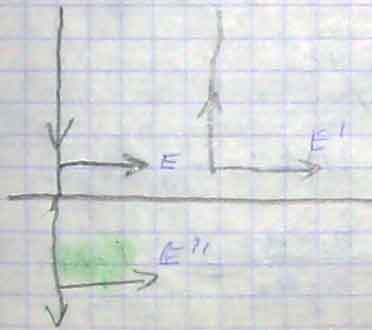
Соотношение между амплитудами и фазами падающей, отражённой и преломлённой волн.

Рассмотрим случай нормального падения световой волны на границу раздела двух сред с n₁ и n₂. Е, E’ и E’’ – напряжённости электрического поля в падающей, отражённой и преломлённой волнах.

Из курса электричества известно, что тангенсальная составляющая вектора напряжённости электрического поля не прерывается при переходе через границу, поэтому для данного случая можно записать:

– вектор Поинтига представляет собой плотность потока энергии. S=EH= . (2)

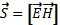
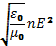
Подставляя (2) в (3): 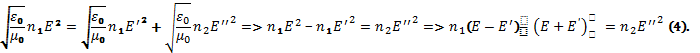Отсюда учитывая (1):.

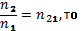
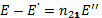
Т.к. . (5)

Получена система уравнений (1) и (5), из которой найдём E’ и E’’.

Найдём выражение для коэффициента отражения R и коэффициента пропускания Т. R представляет собой долю отражённой энергии и равен отношению интенсивности отражённой волны к интенсивности падающей волны: R=I’/I (8).

Т представляет собой отношение преломлённой волны к интенсивности падающей: T=I’’/I (9).

Используя (10) и (8) имеем:

Геометрическая оптика и её законы. Принцип Ферма.

Геометрическая оптика представляет собой раздел физики, который изучает распространение света в виде лучей, независимых друг от друга и подчиняющихся законам отражения и преломления, использую понятия и методы геометрии.

Геометрическая оптика представляет собой предельный случай волновой оптики при условии, что λ->0.

Геометрическая оптика базируется на 4х законах:

Законы прямолинейного преломления света – в однородной изотопной среде свет распространяется по прямой линии, т.е. пренебрегается явление дифракции.

Закон независимости световых лучей. Предполагается, что при пересечении луча не влияют друг на друга. Это справедливо для не очень больших интенсивностей.

Закон отражения света.

Закон преломления света.

В основу геометрической оптики может быть положен принцип Ферма.

Свет распространяется по пути, не прохождение которого ему надо затратить минимальное время. Этот принцип может быть сформулирован с использованием понятия оптическая длина пути света.

Время t прохождения света между двумя точками в неоднородной среде с n можно записать:

, где L – оптическая полная длина дуги (1).

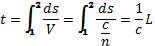
Из (1) видно, что t будет минимально при L->min.

Поэтому можно сформулировать: свет распространяется по такому пути, оптическая длина которого минимальна.

Пути света, у которых оптические длины равны, называются таутохромными.

Источник

В каком случае фаза колебаний волны меняется на противоположную при отражении

Гигантский магнитоакустический эффект в антиферромагнетике KMnF3: Магнитные колебания и волны: частоты «расталкиваются»

Бесстолкновительные ударные волны

Акустика

Когерентный и некогерентный свет: когерентные колебания

Оптические атомные часы

Конец жизни звезд: вторая космическая скорость

Во что превращаются звезды в конце жизни: вторая космическая скорость

Аномальное сопротивление плазмы

Андерсоновская локализация

Зонная структура электронного энергетического спектра в твердых телах. Модели свободных и сильно связанных электронов.: 1.1.3. Фазовая скорость и дисперсия волн де Бройля

Амплитудная модуляция

Интерференция света: геометрическая разность хода

Гигантский магнитоакустический эффект в антиферромагнетике KMnF3

Синее-синее небо, аргон и абсолютно черное тело

Акустические течения

Физические основы строения и эволюции звезд: tex2html637

Атомное кино

Радиоактивные газовые зонды в дифузионно-структурном анализе твердых тел и твердофазных процессов: (1)

Эффект Казимира

Интерференция света: Интерференция плоских волн

Колебания и волны. Лекции.

Отражение волны на конце шнура.

Мы уже упоминали в начале этой лекции, что волна, достигнув конца шнура, отразится. Характер этого отражения зависит от условий закрепления конца шнура (граничных условий).

Рассмотрим вначале более подробно процесс отражения импульса от закрепленного конца шнура.

На рис. 4.9 показаны последовательные стадии отражения импульса треугольной формы, где пунктиром изображены «падающий» и «отраженный» импульсы. Если длительность импульса равна 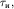то его протяженность вдоль струны равна Пусть в момент времени он добежит до конца струны. В последующие моменты времени шнур будет воздействовать на кронштейн, к которому прикреплен его конец, с переменной силой, перпендикулярной направлению движения импульса. Эта сила в момент времени начинает тянуть кронштейн вверх. В течении времени она остается постоянной, и в момент времени становится равной нулю. По третьему закону Ньютона с такой же силой кронштейн действует вниз на конец шнура. В момент времени шнур становится прямым. Однако часть шнура длиной продолжает двигаться вниз по инерции. При шнур тянет кронштейн вниз, и это действие прекращается при Естественно, что кронштейн воздействует на конец шнура с силой, направленной вверх, тормозя движение его элементов вниз. Окончательно поперечное действие шнура на кронштейн прекратится при когда сформируется отраженный импульс, имеющий противоположную (по отношению к падающему) полярность.

Рис. 4.9.

Если по шнуру бежит гармоническая волна, то по достижении закрепленного конца шнура возникает обращенная отраженная волна. Чтобы учесть изменение ее полярности, в аргумент уравнения отраженной волны добавляют фазовый сдвиг Поэтому говорят, что в этом случае при отражении фаза волны скачком меняется на или «теряется полволны». В общем случае при произвольных граничных условиях сдвиг фазы может меняться в интервале Поясним сказанное простейшим расчетом.

Пусть по шнуру бежит гармоническая волна. Достигнув конца шнура при она будет отражаться (рис. 4.10). Смещение любого участка струны, имеющего координату определяется как суперпозиция бегущей и отраженной волн:

(4.33)

Рис. 4.10.

В (4.33) учтено, что отраженная волна, во-первых, проходит расстояние «туда и обратно», равное и, во-вторых, приобретает сдвиг фазы при ее отражении. Проведем суммирование в (4.33) и получим:

(4.34)

Полагаем, что амплитуда волны 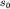остается постоянной при распространении и не меняется при отражении.

Это выражение является уравнением стоячей волны. Основные ее характеристики могут быть сведены к следующим:

1. В стоячей волне все участки шнура колеблются с одинаковой частотой и в фазе, однако амплитуда этих колебаний меняется вдоль шнура, т.е. стоячая волна является модой колебаний.

2. Амплитуда колебаний в стоячей волне получается из (4.34) равной:

(4.35)

Из этого выражения видно, что некоторые участки шнура колеблются с амплитудой, равной Это так называемые «пучности» стоячей волны. С другой стороны, существуют участки, которые остаются неподвижными, т. к. для них амплитуда Это так называемые «узлы» стоячей волны.

На рис 4.11 изображены смещения фрагмента струны для трех последовательных моментов времени и Нетрудно показать, что расстояния между двумя соседними узлами, указанными точками, равно расстоянию между двумя соседними пучностями, отмеченными крестиками, и составляет величину

Рис. 4.11.

3. Все части шнура, лежащие между двумя соседними узлами, совершают колебания в фазе. При переходе через узел фаза колебаний скачком изменяется на что соответствует изменению знака

4. На конце шнура амплитуда

(4.36)

Для закрепленного конца шнура и На рис. 4.10 показан участок в полволны, который «теряется» при таком отражении. Расположенная правее этого участка часть волны, изображенная пунктиром в области после поворота направления распространения как раз и будет являться волной, отраженной в закрепленной точке

Обратимся теперь к отражению волны от свободного конца шнура. Технически это можно реализовать, если конец шнура привязать к тонкой и легкой нити, которая служит лишь для создания натяжения шнура с силой

Рис. 4.12.

Возбуждение стоячих волн в шнуре. Моды колебаний.

Пусть кронштейн, к которому привязан левый конец шнура, совершает гармонические колебания где — очень малая амплитуда. Поэтому левый конец шнура можно считать закрепленным. По шнуру побежит гармоническая волна (рис. 4.13), которая после отражения от правого закрепленного конца приобретет сдвиг фазы, равный Добежав до левого конца, она еще раз отразится, а сдвиг фазы станет равным

Рис. 4.13.

Двукратно отраженная волна наложится на постоянно бегущую вправо гармоническую волну. Если сдвиг фазы колебаний у этих волн будет кратным величине то результатом наложения будет волна, амплитуда которой превышает амплитуду исходной бегущей волны. Таким образом, бегущая волна усилится. Если бы не было потерь энергии, то нарастание амплитуды при многократном отражении было бы неограниченным. Однако потери, как мы не раз видели, также увеличатся с ростом амплитуды. Поэтому колебания установятся: в систему будет закачано некоторое количество энергии, а дальнейший приток ее будет равен диссипации.

(4.37)

Поэтому частота должна удовлетворять условию

(4.38)

где

(4.39)

Конфигурацию колеблющейся струны на частотах (4.39) можно легко нарисовать, когда амплитуды бегущей и отраженной волн не меняются вдоль шнура и равны между собой. Очевидно, что это будут стоячие волны, рассмотренные нами выше и соответствующие одинаковым граничным условиям : на обоих концах шнура должны быть узлы смещения.

Источник