в каком случае фирма максимизирует прибыль
Раздел 2. Теория производства
Тема 2. Поведение предприятия в условиях совершенной конкуренции
Практическая работа 2
Целью данного практикума является закрепление основных положений рыночного механизма в условиях совершенной конкуренции.
Задачами практикума являются:
Оглавление
Задачи на максимизацию прибыли и минимизацию убытков в условиях совершенной конкуренции
Задача 1
Постановка задачи: Используя данные таблицы, определите оптимальный объем производства фирмы – совершенного конкурента, если цена реализации данного товара 30 у. е.:
Технология решения задачи: В условиях совершенной конкуренции условием максимизации прибыли является МС = Р, поэтому необходимо определить МС. Продолжим таблицу.
МС = Р при объеме 10 ед. – это оптимальный объем производства.
Ответ: 10 ед. продукции.
Задача 2
Постановка задачи: Определите, какой объем лучше выпускать предприятию, продающему товар по цене, равной 15 у. е., и имеющему следующие затраты на производство и реализацию продукции (см. таблицу). Определите максимальную прибыль.
Технология решения задачи: Для решения задачи надо определить предельные затраты и сравнить их с ценой (см. таблицу, расположенную ниже). При объеме производства равном 1 ед., а также при объеме, равном 7 ед. продукции, выполняется условие совершенной конкуренции МС = Р. Но прежде чем сделать вывод об оптимальном объеме производства, надо подсчитать прибыль, а до этого общую выручку.
Из таблицы видно, что при данной цене товара нет оптимального объема, т. к. производство убыточно, но убытки минимальны, когда МС = Р, поэтому предприятию следует выпускать именно этот объем производства, чтобы минимизировать убытки.
Задача 3
Постановка задачи: Объем выпуска фирмы в условиях совершенной конкуренции 100 т, цена товара 2 тыс. у. е., общие издержки (100 т) составляют 130 тыс. у. е. Определите общую прибыль фирмы.
Технология решения задачи: определяем общую выручку TR = 100 * 2 = 200 тыс. у. е. и сравниваем ее с общими затратами: 200 – 130 = 70 тыс. у. е.
Задача 4
Технология решения задачи: Найдем предельные издержки: 
Задача 5
Постановка задачи: Фирма, совершенный конкурент, имеет две точки реализации. Спрос в первой определяется функцией
q1 = 80 – P, q2 = 100 – 2P. Определите, какой объем продукции надо произвести, если на рынке установилась цена 42 у. е.
Технология решения задачи: Надо определить спрос на первой и второй точке продаж при цене 42 у. е.: q1 = 80 – 42 = 38, q2 = 100 – 2 * 42 = 16. Общий объем спроса: 38 + 16 = 54 ед. Этот объем и надо произвести.
Ответ: 54 ед. продукции.
Задача 6
Постановка задачи: Общие издержки фирмы, совершенного конкурента, определяются формулой ТС = 10 Q 2 + 24 Q + 88. Оптимальным для фирмы является производство 16 ед. продукции. Определите, какая цена установилась на рынке.
Технология решения задачи: Оптимальный объем производства фирмы-конкурента определяется, исходя из условия
МС=Р, поэтому необходимо найти МС 16-й ед. продукции. 
Задача 7
Задача 8
Постановка задачи: Фирма планирует выпустить учебник. АС составляют 4 долл. + 4000 долл./Q, где Q – количество учебников, выпущенных за год. Планируемая цена книги 6 долл. Каков должен быть годовой тираж учебника, соответствующий точке безубыточности?
Технология решения задачи: В точке безубыточности АС = Р, т. е. 4 + 4000/Q = 6. 4000/Q = 2, Q = 2000 ед.
Задача 9
Постановка задачи: Используя данные таблицы, определите, ниже какого уровня должна опуститься цена, чтобы фирма – совершенный конкурент прекратила производство в коротком периоде?
10.3. Условия максимизации прибыли
В условиях совершенной конкуренции цена продукции является для фирмы заданной величиной (рис. 10.2).
Рис. 10.2. Максимизация прибыли
Любое количество товаров продается по одной и той же цене. Средний доход АЯ также будет постоянным и равным предельному доходу МЯ, так как каждая последующая единица товара будет продана по той же цене, что и предыдущая. В данном случае цена Р равна среднему доходу АЯ и предельному доходу МЯ:
Совмещая все кривые на одном графике (рис. 10.3), фирма максимизирует прибыль в точке пересечения О кривых предельного дохода МЯ и предельных издержек МС.
 Рис. 10.3. Максимизация прибыли в точке пересечения |
Пересечение предельного дохода МЯ с кривой предельных издержек МС (рис. 10.4) происходит в двух точках М и К.
В точке М предельные издержки снижаются, следовательно, прибыль возрастает. Фирма будет увеличивать выпуск продукции до точки К, что предполагает максимизацию прибыли.
Максимальная прибыль будет привлекать в отрасль новые фирмы, что обусловит увеличение предложения и снижение цены товара, тем самым и снижение прибыли фирм.
В условиях совершенной конкуренции в длительном периоде вход в отрасль и выход фирм из нее определяется равенством цены средним издержкам, предельному доходу и предельным издержкам:
Б. Как фирма максимизирует прибыль



А. Условие равновесия
Равновесие фирмы в коротком периоде
В теории рынков коротким называется период, когда число фирм в отрасли и размер капитала каждой фирмы фиксированы, но фирмы могут изменить выпуск, изменяя количество переменных факторов, в частности труда.
Цель фирмы – максимизация прибыли. Прибыль (П) – это разница между выручкой (TR) и совокупными затратами фирмы (TC):
Как выручка, так и затраты фирмы есть функции выпуска (q). Поскольку в функции выручки (TR=P*q) рыночная цена неподконтрольна совершенно конкурентной фирме, задача последней состоит в определении выпуска, при котором ее прибыль станет максимальной.
Фирма максимизирует прибыль при таком выпуске, когда ее предельный доход становится равен предельным затратам:
Равенство MR=MC как условие максимизации прибыли можно обосновать логически. Каждая дополнительная единица выпуска приносит фирме какую-то дополнительную выручку (предельный доход), но и требует дополнительных затрат (предельные затраты). Если предельный доход превышает предельные затраты при некотором объеме выпуска, то фирма получает больше прибыли, производя еще одну единицу продукции. Напротив, если предельный доход при данном выпуске оказался ниже предельных затрат, фирма может увеличить прибыль, уменьшая выпуск на одну единицу. Если, наконец, предельный доход совпадает с предельными затратами, то никакое изменение производства не способно увеличить прибыль – достигнутый выпуск оптимален. Фирма находится в состоянии равновесия – для получения максимальной прибыли ей не надо ни увеличивать, ни сокращать свой выпуск.
Поскольку предельный доход совершенно конкурентной фирмы равен цене товара, вышеприведенное равенство принимает вид:
Если функция совокупных (переменных) затрат фирмы непрерывна и дифференцируема, то для нахождения равновесного выпуска совершенно конкурентной фирмы надо сначала найти функцию предельных затрат (взяв производную функции совокупных или переменных затрат по выпуску), а затем приравнять ее к цене товара.
Рассмотрим на условном примере, как конкурентная фирма достигает точки равновесия. Пусть даны постоянные и переменные затраты фирмы, а также цена, по которой она продает свой товар. На этой основе можно рассчитать изменения средних и предельных затрат, выручки и прибыли фирмы в зависимости от изменения ее выпуска (табл. 13):
Табл13. Максимизация прибыли конкурентной фирмы
| q | FC | VC | TC | AFC | AVC | AC | MC | P=MR | TR | П |
| -60 | ||||||||||
| -62 | ||||||||||
| -52 | ||||||||||
| 20,0 | 21,3 | 41,3 | -34 | |||||||
| -12 | ||||||||||
| 16,4 | 28,4 | |||||||||
| 10,0 | 16,7 | 26,7 | ||||||||
| 8,6 | 17,7 | 26,3 | ||||||||
| 7,5 | 19,3 | 26,8 | ||||||||
| 6,7 | 21,6 | 28,2 | ||||||||
| -10 |
В данном случае предельные затраты сперва убывают, а затем возрастают, т.е. мы сталкиваемся с усложненными функциями затрат (тема 5, п. 4В).
Предположим, фирма случайно остановилась на выпуске 5 ед. Предельный доход от выпуска еще одной единицы продукции (он же цена товара) равен 30, тогда как предельные затраты составляют только 18. Поэтому фирма увеличивает выпуск, и ее прибыль возрастает на 12 (с 8 до 20). Пусть фирма вначале выбрала выпуск 9 ед. Предельный доход при этом равен, как всегда, 30, а предельные затраты составляют 40. Превышение предельных затрат над предельным доходом является сигналом для сокращения производства до 8 ед., что увеличивает прибыль на 10 (с 16 до 26). Наконец, при производстве 8 ед. товара предельный доход совпадает с предельными затратами (30=30), и прибыль является максимальной (26). Именно на таком выпуске наша фирма и останавливается.
Внимательный читатель может возразить, что в приведенном примере точно такая же прибыль получается и при выпуске 7 ед. товара. Дело, однако, в том, что наш расчет предельных затрат является лишь приблизительным. Точно предельные затраты рассчитываются как приращение совокупных (переменных) затрат при очень небольшом изменении выпуска. Представьте себе, что при производстве 7,99 ед. товара предельный доход еще чуть-чуть превышает предельные затраты. Значит, выгодно произвести еще одну сотую товара, после чего предельный доход и предельные затраты сравняются. Иными словами, здесь используется предпосылка, что продукт является бесконечно делимым: можно произвести еще один грамм масла, еще один гвоздь или еще одну автомашину при их многотысячном выпуске.
Точку равновесия совершенно конкурентной фирмы можно показать, соединив на рисунках, с одной стороны, функции выручки и совокупных затрат, а, с другой стороны, функции предельного дохода (цены) и предельных затрат (рис. 13):
Рис. 13. Равновесие совершенно конкурентной фирмы
Пока производство возрастает от нуля до q1, каждая следующая единица выпуска увеличивает убытки фирмы, поскольку в этом интервале предельные затраты превосходят предельный доход (рис.13-Б). Соответственно при выпуске q1 убытки достигают максимума. На рис. 13-А мы видим, что при выпуске q1 расстояние между функциями TC и TR максимально – совокупные затраты превосходят выручку фирмы на максимально возможную величину.
Фирма продолжает увеличивать выпуск и переходит в зону, где предельный доход оказывается выше предельных затрат (MR>MC на рис. 13-Б). В этой зоне дополнительные единицы выпуска начинают приносить прибыль. Тем не менее из-за груза прошлых убытков общая прибыль еще остается отрицательной вплоть до достижения выпуска q2, при котором убывающие средние совокупные затраты (совокупные затраты на единицу выпуска) становятся равны цене. В этой точке, называемой точкой безубыточности, прибыль (убытки) равны нулю. На рис. 8-3А точка безубыточности – это точка, где выручка становится равна совокупным затратам.
Пройдя точку безубыточности, фирма покидает зону убыточности и переходит в зону прибыльности, поскольку после выпуска q2 средние совокупные затраты на рис.13-Б оказываются ниже цены. При этом при выпуске q3 средние совокупные затраты минимальны, т.е. разница между ценой и средними совокупными затратами максимальна. Последнее означает, что при выпуске q3 максимальна прибыль на единицу производимой продукции.
Фирма, однако, продолжает наращивать производство, ибо ее цель – получить максимальную общую прибыль. Это достигается при выпуске q4, когда предельный доход на рис 8-3Б равен предельным затратам. Выручка фирмы (TR=P*q) в этой точке равна площади P*Eq4O, а совокупные затраты (TC=AC*q) – площади ONMq4. Таким образом, максимальная прибыль фирмы (П=TR-TC) составляет площадь P*EMN.
При выпуске q4 прибыль максимальна и на рис. 8-3А, поскольку при данном выпуске расстояние между функциями выручки и совокупных затрат становится максимальным – выручка превышает затраты на максимально возможную величину.
Если же выпуск q4 будет превзойден, прибыль начнет убывать, т.к. предельные затраты на рис. 8-3Б превысят предельный доход. Тем не менее, прибыль останется положительной вплоть до выпуска q5, при котором возрастающие средние совокупные затраты достигнут уровня цены. Мы имеем вторую точку безубыточности, за которой начинается зона убытков.
На рис. 8-3А вторая точка безубыточности, достигаемая при том же объеме выпуска (q5) – это точка, где выручка вновь становится равна совокупным затратам.
Максимизация прибыли
Вы будете перенаправлены на Автор24
Сущность и определение
Максимизация прибыли – это процесс, целью которого является получение наивысших выгод от коммерческой деятельности. Каждое коммерческое предприятие всегда стремится увеличить собственную прибыль и сделать прибыль максимально высокой.
Сущность понятия исходит из закона экономической теории о максимизации полезности. То есть цели коммерческой фирмы всегда направлены на получение максимальной прибыли при ограниченных ресурсах: труд, капитал, предпринимательство, земля.
Важным критерием максимизации прибыли является объем выпуска продукции (предоставляемых услуг или работ). Так как именно от данного показателя напрямую зависит получаемая прибыль.
Важные факторы, влияющие на прибыль:
Для того, чтобы выявить наилучший объем выпуска и максимизировать прибыль, на коммерческой фирме обычно используется два подхода:
На решение по максимизации прибыли сильное влияние оказывает период оценки:
Рассмотрим два подхода к максимизации прибыли.
Метод общих доходов и издержек при максимизации прибыли
На графике необходимо представить следующие кривые:
По оси абсцисс на графике должен располагаться объем производства, а по оси ординат – издержки, выраженные в денежном эквиваленте.
График модели представлен на схеме 1 ниже.
Готовые работы на аналогичную тему
Если проводить оценку графика по фактическим данным, то можно сделать следующие выводы:
Метод предельных доходов и издержек при максимизации прибыли
Далее рассмотрим основные условия, при которых возможна максимизация прибыли для коммерческой фирмы, для методов рассмотренных выше.
Условия
Рассмотрим главные условия, при которых возможна максимальная прибыль для коммерческой фирмы:
Правила максимизации прибыли
Правило максимизации прибыли означает, что предельные продукты всех факторов производства в стоимостном выражении равны их ценам или что каждый ресурс используется до тех пор, пока его предельный продукт в денежном выражении не станет равнозначен его стоимости.
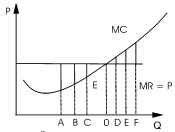
Увеличение выпуска продукции повышает прибыль предприятия. Но только в том случае, если доход от продажи дополнительной единицы продукции превышает издержки производства данной единицы (MR больше MC). На рис. 1 этому условно соответствуют объемы выпуска А, В, С. Получаемые в результате выпуска этих единиц дополнительные прибыли выделены на рисунке жирными линиями.
MR – предельный доход;
MC – предельные издержки
Рис. 1. Правило максимизации прибыли
Когда издержки, связанные с выпуском еще одной единицы продукции, выше приносимого за счет ее реализации дохода, то предприятие лишь увеличивает свои убытки. Если MR меньше MC, то производить дополнительный товар невыгодно. На рисунке эти убытки отмечены жирными линиями над точками D, E, F.
В этих условиях максимальная прибыль достигается при том объеме производства (точка О), где кривая предельных издержек в своем возрастании пересечет кривую предельного дохода (MR = MC). Пока MR больше MC, увеличение производства дает возрастающую меньше прибыль. Когда же после пересечения кривых устанавливается соотношение MR MC, к увеличению прибыли ведет сокращение производства. Прибыль растет при приближении к точке равенства предельных издержек и дохода. Максимум прибыли достигается в точке О.
В условиях совершенной конкуренции предельный доход равен цене товара. Поэтому правило максимизации прибыли может быть представлено в другом виде:
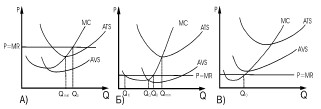
На рис. 2 правило максимизации прибыли применено к процессу выбора оптимального объема производства для трех важнейших рыночных ситуаций.
Рис. 2. Оптимизация объема производства в условиях максимизации прибыли А), минимизации убытков Б), и прекращения производства В).
В условиях совершенной конкуренции максимизация прибыли (минимизация убытков) достигается при объеме производства, соответствующем точке равенства цены и предельных издержек.
Рис. 2 показывает, как происходит выбор в условиях максимизации прибыли. Максимизирующая прибыль предприятия устанавливает объем своего производства на уровне Qo, соответствующем точке пересечения кривых MR и MC. На рисунке она обозначена точкой О.