в каком случае графики параллельны

Прямые на координатной плоскости

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

где c – произвольное число, и изображены на рис. 13, 14, 15.

где p, q, r – произвольные числа.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

Источник

Линейная функция, ее свойства и график

теория по математике 📈 функции

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

Вписываем в таблицу значения у:

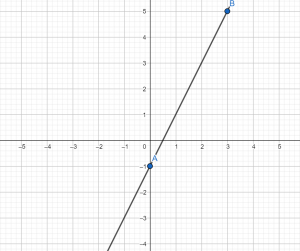
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5),

Итак, по формуле мы видим, что угловой коэффициент — положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

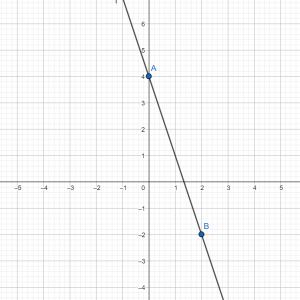
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

Пример №3

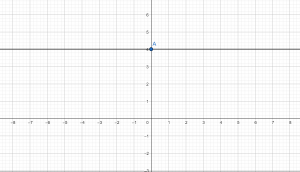
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

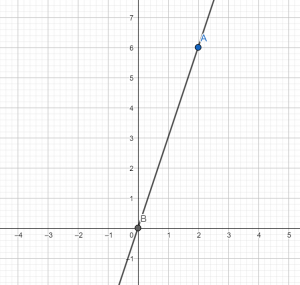
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

График данной функции зависит от k и b.

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

Урок по математике на тему «взаимное расположение графиков функции»

Ищем педагогов в команду «Инфоурок»

Класс: 6 б Урок: 164 День: 8.04.15

Тема урока: Взаимное расположение графиков линейных функции

Тип урока: Урок ознакомления с новым материалом.

Обеспечить условия для:

Раскрытия геометрического смысла коэффициента k и b функции y=kx + b

Введения понятия “угловой коэффициент”;

Формирования умений по внешнему виду формул задающих линейные функции устанавливать взаимное расположение графиков этих функций;

Формирования умений строить графики линейных функций.

Обеспечить условия для:

Самостоятельного добывания знаний, осмысленного отношения к своей деятельности;

Самостоятельности мышления: выделять главное, видеть общую закономерность и делать обобщенные выводы;

Формирования культуры учебной деятельности;

Личностного саморазвития учащихся;

Развития критического мышления;

Развития глазомера учащихся.

Обеспечить условия для:

Воспитания ответственного отношения к учению;

Воспитания культуры общения.

Создание ситуации успеха.

Формы: Фронтальный опрос, самостоятельная работа, индивидуальная работа.

Организационный момент. (1 мин.)

Актуализация опорных знаний. (5-6 мин.)

Введение в тему. Постановка учебных задач. (3-4 мин.)

Ознакомление с новым материалом. (12-15 мин.)

Домашнее задание. (1-2 мин.)

1. Организационный момент.

Цель: Обеспечить рабочую обстановку на уроке.

Учитель приветствует учащихся, проводит проверку готовности класса к уроку.

Дежурные помогают учителю.

2. Актуализация знаний.

Цель: Организовать познавательную деятельность учащихся.

– Назовите известные вам функции.

– Какая функция называется линейной?

– Какая функция называется прямой пропорциональностью?

Среди формул (на доске):

, , , , , , найдите те, которые задают линейную функцию. Для этих формул укажите и .

Какие из формул задают прямую пропорциональность?

Что является графиком линейной функции?

Что является графиком прямой пропорциональности?

Скольких точек достаточно для построения прямой?

Как могут располагаться две произвольные прямые на плоскости?

– Линейная функция и прямая пропорциональность.

– Линейной функцией называется функция, которую можно задать формулой вида ,

где — независимая переменная, и — некоторые числа.

– Прямой пропорциональностью называется функция, которую можно задать формулой вида

, — независимая переменная, — не равное нулю число.

.

Графиком линейной функции является прямая.

График прямой пропорциональности – прямая.

Две прямые могут быть параллельными, могут пересекаться и совпадать.

Постановка учебных задач.

Цель: Обеспечить целеполагание.

Мы с вами знаем, что графиком линейной функции является прямая, поэтому графики двух линейных функций тоже могут быть параллельными, могут пересекаться и совпадать.

А теперь выясним, что нового мы должны узнать на уроке, что выяснить, чему научиться?

На основе предыдущих рассуждений попытайтесь самостоятельно сформулировать тему урока.

Учитель корректирует ответы учащихся.

Тема урока: Взаимное расположение графиков линейных функций.

Выясним, что должны узнать на уроке.

Попытайтесь самостоятельно поставить цель, которую вы хотите достичь.

Учителем на доске заранее подготовлена запись:

После наиболее точной формулировки цели урока учащимися, учитель записывает цель урока на доске.

Возможные ответы учащихся:

– Расположение графиков линейных функций;

– Взаимное расположение графиков линейных функций;

Ученики записывают тему урока в тетрадь.

– Должны рассмотреть параллельность, пересечение и совпадение графиков линейных функций;

– Графики, каких линейных функций параллельны, пересекаются, совпадают;

– От чего зависит параллельность, пересечение, совпадение графиков линейных функций;

– В каком случае графики двух линейных функций параллельны, в каком случае пересекаются, в каком случае совпадают. (То, что говорят дети, учитель быстро записывает на доске).

4. Ознакомление с новым материалом.

Цель: Создать условия для

ознакомления учащихся с новым материалом.

На доске записаны три группы заданий:

В одной системе координат постройте графики функций:

1. , 2. 3. .

В одной системе координат постройте графики

1. , 2. , 3.

В одной системе координат постройте графики

1. , 2. , 3. .

Первичное осмысление и закрепление изученного.

Цель: Создать условия для первичного осмысления и закрепления полученных знаний.

Учитель знакомит учащихся с заданиями.

– Построение графика функции под цифрой 3 выполняете, если уже построено по два графика в каждой группе заданий.

– В итоге выполнения заданий у вас в тетради должно быть изображено три системы координат, в каждой из которых обязательно по два графика. У сильных учащихся в тетрадях возможно – по три графика.

Учитель даёт возможность каждому учащемуся самостоятельно определиться с формой работы.

Те учащиеся, которые уверены в своих силах и могут самостоятельно построить все графики садятся на левый ряд и работают самостоятельно. Учитель контролирует их деятельность.

Остальные, которые не уверены в своих силах, садятся на правый ряд и выполняют построение вместе с учителем, работая по одному у доски.

После выполнения заданий на доске изображены три системы координат, в каждой из которых по два графика, а у сильных учащихся в тетрадях возможно – по три графика.

– Обратите внимание на доску:

Работаем над заданием №1.

– Посмотрите на формулы, задающие графики этих функций, что вы заметили?

– Обратите внимание на то, как расположены графики этих функций?

– Какой вывод можно сделать, сопоставив запись формул, задающих функции и взаимное расположение их графиков?

– Как графики данных функций располагаются по отношению к оси ох?

– Верно, и этот угол зависит от коэффициента , который называется угловым коэффициентом прямой графика функции .

Отметьте на чертеже углы наклона графиков функций к оси ох.

Работаем над заданием №2.

Учитель задаёт аналогичные вопросы, а также обращает внимание на то, в какой точке пересекаются прямые.

Работаем над заданием №3.

Учитель задаёт аналогичные вопросы, что и при работе над заданием №1.

– Откройте учебник на странице 65 и проверьте, правильные ли мы с вами сделали выводы.

– Обратите внимание на цели, которые вы поставили в начале урока.

– На какой вопрос осталось ответить?

– В каком же случае графики двух линейных функций совпадают?

Запишите выводы в тетрадь.

Ученики выполняют задания индивидуальных рабочих листов. Приложение1.

– Коэффициенты при одинаковые.

– Графики данных функций параллельны.

– Когда коэффициенты равны, то графики параллельны.

– Графики линейных функций параллельны, если коэффициенты при одинаковые.

– Графики пересекают ось.

– Графики данных функций наклонены к оси ох под одним и тем же углом.

– Коэффициенты при различные, а одинаковые.

– Прямые пересекаются в точке (0; 2).

– Графики пересекаются, когда одинаковые.

Точка пересечения (0; ).

– Графики пересекаются, когда коэффициенты при различны.

– Коэффициенты при различные и различные.

– Графики пересекаются, когда коэффициенты при различны.

Открывают учебник и читают:

Графики двух линейных функций, заданных формулами вида , пресекаются, если коэффициенты при различны и параллельны, если коэффициенты при одинаковые.

– В каком случае графики двух линейных функций совпадают.

– Графики двух линейных функций совпадают, в том случае, если совпадают и .

Цель: Создать условия

для формирования навыка

– Что каждый из вас сегодня узнал, понял, открыл?

– Что понравилось особенно, что бы хотелось выполнить еще раз?

– Что не понравилось и почему?

– Что бы вы хотели изменить?

7. Домашнее задание.

Цель: Дать инструкцию по выполнению домашнего задания.

№ 1337, 1339, 1341(а, в) – для всех.

Цель: Подвести итоги урока, обобщить и систематизировать знания, полученные на уроке.

— Что делали на уроке?

— Что нового узнали на уроке?

Учитель оценивает работу: учитывает правильность, самостоятельность, оригинальность.

Источник

Урок алгебры по теме : «Взаимное расположение графиков линейных функций»

Ищем педагогов в команду «Инфоурок»

Тема: «Взаимное расположение графиков линейных функций»

1. Отработка навыков построения графиков функции вида y = kx + b ;

2. Выяснение влияния значений k и b на положение графиков;

3. Выяснение влияния значения параметра k на взаимное расположение графиков линейных функций.

4. формирование навыков работы с программой ADVANCED GRAPHER ;

1.Воспитание коммуникативной и информационной культуры учащихся;

2.Умение учащихся данной группы построить на короткое время взаимодействие, исходя из особенностей задач.

1. Интеллектуальное, эмоциональное, личностное развитие ученика;

2. Развитие осмысленного отношения к своей деятельности;

3. Развитие самостоятельности мышления: выделять главное, видеть общую закономерность и делать обобщённые выводы.

Девизом к нашему уроку я хочу предложить такие слова «Каждое дело творчески, иначе зачем?»

2. Актуализация знаний

— На сколько групп вы распределили данные функции? (На две)

— Какие функции отнесли к первой группе и почему? (Графиками данных функций не являются прямыми.)

Группы указанные учащиеся записывают на доске

— Какие функции отнесли ко второй группе и почему? (Графиками данных функций являются прямые.)

— Обратите внимание на вторую группу формул.

— Как называются функции из второй группы? (линейные)

— Назовите коэффициент при x в формулах этих линейных функций? (2,-3,-0)

— Сколько точек достаточно для построения графиков этих функций? (двух)

— Как могут располагаться две произвольные прямые на плоскости? ( Две прямые могут быть параллельными, могут пересекаться и совпадать)

3. Введение в тему. Постановка учебных задач на уроке.

Мы с вами знаем, что графиком линейной функции является прямая, поэтому графики двух линейных функций тоже могут быть параллельными, могут пересекаться и совпадать.

А теперь выясним, что нового должны узнать на уроке, что выяснить, чему научиться? (Расположение графиков линейных функций)

На основе предыдущих рассуждений попытайтесь самостоятельно сформулировать тему урока. ( Взаимное расположение графиков линейных функций)

Учитель корректирует ответы учащихся.

Давайте запишем в тетрадь тему урока: «Взаимное расположение графиков линейных функций»

Выясним, что должны узнать на уроке.

Попытайтесь самостоятельно поставить цель, которую вы хотите достичь.

— Должны рассмотреть параллельность, пересечение и совпадение графиков линейных функций;

— Графики, каких линейных функций параллельны, пересекаются, совпадают;

— От чего зависит параллельность, пересечение, совпадение графиков линейных функций)

4.Ознакомление с новым материалом.

В одной системе координат постройте с помощью ADVANCED GRAPHER графики функций:

Что можно сказать про графики линейных функций? (они параллельны)

Что можно сказать про коэффициенты b и k в формулах? ( k равны, b не равны)

Вывод? (если у линейных функций угловой коэффициент одинаковый, то их графики параллельны)

В одной системе координат постройте с помощью ADVANCED GRAPHER графики функций:

y =- x +3; y =1,5 x +3; y =0,25 x +3

Что можно сказать про графики линейных функций? (они пересекаются в одной точке (0;3))

Что можно сказать про коэффициенты b и k в формулах? ( b равны, k не равны)

Вывод? (график линейной функции пересекает ось OY в точке (0; b ))

— Обратите внимание на цели, которые вы поставили в начале урока. На какой вопрос осталось ответить? (в каком случае графики двух функций совпадают)

Динамическая пауза (этап физической разрядки).

Зарядка. Мы хорошо поработали, пришло время отдохнуть, а заодно проверить, как вы помните влияние коэффициентов на график функции. После такой работы нужно потянуться и распрямить свой позвоночник.

Мы засиделись. Нужно расправить свои плечи и потянуться. Встанем. Выпрямимся. Начинаем нашу разминку.

Ось ординат. Раз. Два. Потянулись. Ось абсцисс. Потянулись.

k – положительное. Наклон вправо – к положительной полуоси абсцисс. Потянулись.

k – отрицательное. Наклон влево – к отрицательной полуоси абсцисс. Потянулись.

у = 2х – 8 у = 2 – 3х у = – 2х – 11 у = 5 + х у = – 5х + 8 у = 9х – 2 у = 4х + 1 у = 2х – 8 у = – х +3 у = – 2 – 5х у = 2х – 4

6.Первичное осмысление и закрепление изученного.

1 группа. Работа с карточкой.

В одной системе координат с помощью ADVANCED GRAPHER построены графики функций

Определите по графику координаты точки их пересечения и найдите сумму этих координат.

В одной системе координат с помощью ADVANCED GRAPHER построены графики функций

Определите по графику координаты точки их пересечения и найдите сумму этих координат.

Каждый ученик оценивает свои знания полученные на уроке.

Учитель устанавливает соответствие между поставленными задачами и результатами, выносит коррективы, анализирует учебную деятельность.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Источник