в каком случае используются линейные законы ланчестера а в каком квадратичные

Законы Ланчестера

Законы Ланчестера — математические формулы для расчета относительных сил пары сражающихся сторон. Эта статья касается вооруженных сил.

Уравнения Ланчестера — это дифференциальные уравнения, описывающие зависимость между силами сражающихся сторон A и D как функцию от времени, причем функция зависит только от A и D. [1]

В 1916 году, в разгар первой мировой войны, Фредерик Ланчестер разработал систему дифференциальных уравнений для демонстрации соотношения между противостоящими силами. Среди них есть так называемые Линейные законы Ланчестера (для войны древности) и Квадратичные законы Ланчестера (для войн начала XX века с применением дальнобойных орудий, таких как огнестрельное оружие).

Содержание

Линейный закон Ланчестера

В древней битве, например между фалангами воинов, вооруженных копьями, один человек может бороться одновременно только с одним человеком. Если каждый человек убивает ровно одного (или погибает от одного) противника, то ожидаемое число воинов, оставшихся в конце сражения, — это просто разница между численностью большей и меньшей армий (при идентичности применяемого оружия).

Линейный закон применяется также к неприцельному огню по территории противника. Коэффициент убыли зависит от плотности имеющихся целей в целевой области, а также от количества стреляющих орудий. Если две группировки, занимающие одинаковую площадь и использующие одинаковые орудия, ведут огонь случайным образом по площадной цели одинакового размера, они будут убывать одинаковыми темпами до тех пор, пока меньшая группировка в конце концов не будет ликвидирована: большая вероятность поражения одним выстрелом какой-либо единицы крупной группировки уравновешивается большим числом выстрелов направленных на мелкую группировку.

Закон «честного боя»

Квадратичный закон Ланчестера

В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.

Коэффициент убыли(rate of attrition) зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.

Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон. Заметим, что Квадратичный закон Ланчестера не относится к технологической силе, а только к численной силе, поэтому он предполагает N-квадрат-кратное увеличение качества для N-кратного увеличения количества.

Закон концентрации

(Истребительная сила) = (качество оружия) × (количество единиц)

Примечания

Части этой статьи скопированы с разрешения из статьи Эрнеста Адамса, опубликованной на веб-сайте разработчиков компьютерных игр Gamasutra. См. ссылки ниже.

Источник

protvagrad

protvagrad

В 1916 году, в разгар первой мировой войны, Фредерик Ланчестер разработал систему дифференциальных уравнений для демонстрации соотношения между противостоящими силами. Среди них есть так называемые Линейные законы Ланчестера (для войны древности) и Квадратичные законы Ланчестера (для войн начала XX века с применением дальнобойных орудий, таких как огнестрельное оружие).

Линейный закон Ланчестера

В древней битве, например между фалангами воинов, вооруженных копьями, один человек может бороться одновременно только с одним человеком. Если каждый человек убивает ровно одного (или погибает от одного) противника, то ожидаемое число воинов, оставшихся в конце сражения, — это просто разница между численностью большей и меньшей армий (при идентичности применяемого оружия).

Линейный закон применяется также к неприцельному огню по территории противника. Коэффициент убыли зависит от плотности имеющихся целей в целевой области, а также от количества стреляющих орудий. Если две группировки, занимающие одинаковую площадь и использующие одинаковые орудия, ведут огонь случайным образом по площадной цели одинакового размера, они будут убывать одинаковыми темпами до тех пор, пока меньшая группировка в конце концов не будет ликвидирована: большая вероятность поражения одним выстрелом какой-либо единицы крупной группировки уравновешивается большим числом выстрелов направленных на мелкую группировку.

Закон «честного боя»

Квадратичный закон Ланчестера

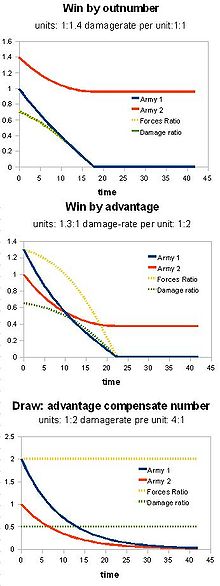
Идеальная модель ущерба, наносимого сторонами друг другу. Пренебрегаются такие параметры, как 1) Размер армии 2) Процент потерь.

В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.

Коэффициент убыли (rate of attrition) зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.

Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон. Заметим, что Квадратичный закон Ланчестера не относится к технологической силе, а только к численной силе, поэтому он предполагает N-квадрат-кратное увеличение качества для N-кратного увеличения количества.

Закон концентрации

(Истребительная сила) = (качество оружия) × (количество единиц)

Источник

В каком случае используются линейные законы ланчестера а в каком квадратичные

«В 1916 году, в разгар первой мировой войны, Фредерик Ланчестер разработал систему дифференциальных уравнений для демонстрации соотношения между противостоящими силами. Среди них есть так называемые Линейные законы Ланчестера (для войн древности) и Квадратичные законы Ланчестера (для войн начала XX века с применением дальнобойных орудий, таких как огнестрельное оружие).

Закон «честного боя»

(Истребительная сила) = (качество оружия) × (количество единиц).

Квадратичный закон Ланчестера

В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.

Коэффициент убыли зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.

Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон.

Прусскому королю Фридриху Великому приписывают авторство изречения, популярного среди полководцев во все времена: «Бог всегда на стороне больших батальонов». То есть, в большинстве случаев, большая армия всегда победит меньшую.

Несмотря на то, что модель Ланчестера имеет существенные ограничения, и, по сути, является приблизительной, она позволяет выявить полезные практические закономерности.

Попробуем погонять туда-сюда цифирки в квадратичном уравнении Ланчестера, и посмотрим, что из этого получится.

Совершенно, очевидно, что при равенстве сил и равенстве вооружения (Е = 1) во встречном бою потери сторон будут равны. Подсчитаем, как будут изменяться потери сторон во встречном бою в зависимости от первоначального соотношения сил:

Е=1 Вариант 1 Вариант 2 Вариант 3 Вариант 4

Исходная численность сторон А 100 100 100 100

Потери сторон А 100 100 100 100

Конечная численность В 0 112 173 282

В данном случае за 100 единиц принята исходная численность соединения: дивизии, полка, корпуса. Из таблицы следует не вполне очевидный вывод: чем больше относительное количественное превосходство одной стороны, тем меньшие абсолютные потери она несет! То есть, одна из сторон, имеющая значительное превосходство в силах, полностью уничтожит слабейшую сторону, понеся, при этом, минимальные потери.*

Е=0,2 Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5

Исходная численность сторон А 100 100 100 100 100

В 100 200 300 400 600

Потери сторон А 11 55 100 100 100

В 100 200 100 70 44

Конечная численность А 89 45 0 0 0

Вариант 1 показывает, что, при равной численности, обороняющиеся уничтожат всех атакующих, понеся при этом незначительные потери. При двукратном количественном превосходстве атакующих, обороняющиеся потеряют половину состава, однако, атакующие погибнут все. В варианте 3 абсолютные потери сторон равны, однако, за счет большей начальной численности, атакующая сторона полностью уничтожает обороняющихся, и продвигается дальше. При соотношении начальной численности войск более 3, атакующие несут тем меньшие абсолютные потери, чем больше их относительное численное превосходство**.

Е = 0,1 Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6

Исходная численность сторон А 100 100 100 100 100 100

В 100 200 300 400 500 600

Потери сторон А 6 23 69 100 100 100

В 100 200 300 156 110 90

Конечная численность А 89 77 31 0 0 0

В 0 0 0 244 390 510

Даже при соотношении численности сторон 3:1 обороняющаяся сторона одерживает победу, полностью истребив атакующих, потеряв, правда, при этом, две трети своего состава. При соотношении сторон 4:1 победу одерживают уже нападающие, но их потери в полтора раза превышают потери обороняющихся. Если соотношение численности 6:1, то нападающие уничтожают обороняющихся, понеся, при этом, меньшие абсолютные потери.

Е=2 Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5

Исходная численность сторон А 100 100 200 300 400

В 200 100 100 100 100

Потери сторон А 100 100 56 40 26

В 13 71 100 100 100

Конечная численность А 0 0 144 260 374

В случае, когда танковые дивизии атакуют пехоту в долговременной обороне, очевидно, применим коэффициент Е = 0,2, рассмотренный выше.

Если же танковые дивизии «В» атакуют пехоту «А» в полевой обороне, то можно приравнять Е = 0,4. Рассчитаем соответствующую таблицу значений.

Е=0,4 Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5

Исходная численность сторон А 100 100 100 100 100

В 100 150 200 300 400

Потери сторон А 23 69 100 100 100

В 100 150 78 45 33

Конечная численность А 77 31 0 0 0

Видно, что две танковых дивизии пробивают оборону пехотной, потеряв при этом, почти целую дивизию. Однако, пехота может сдержать и уничтожить полторы танковых дивизии. Правда, ценой потери двух третей состава. При численном превосходстве 4:1 нападающие теряют лишь одну треть дивизии.

Источник

Законы Ланчестера

Законы Ланчестера (законы Осипова — Ланчестера) — математическая формула для расчета относительных сил пары сражающихся сторон — подразделений вооруженных сил. В статье «Влияние численности сражающихся сторон на их потери», опубликованной журналом «Военный сборник» в 1915 году, генерал-майор Корпуса военных топографов М. П. Осипов [1] [2] описал математическую модель глобального вооружённого противостояния, практически применяемую в военном деле при описании убыли сражающихся сторон с течением времени и, входящую в математическую теорию исследования операций, на год опередив английского математика Ф. У. Ланчестера. Мировая война, две революции в России не позволили новой власти заявить в установленном в научной среде порядке об открытии царского офицера.

Уравнения Ланчестера — это дифференциальные уравнения, описывающие зависимость между силами сражающихся сторон A и D как функцию от времени, причем функция зависит только от A и D. [3]

Содержание

Линейный закон Ланчестера [ | ]

В древней битве, например между фалангами воинов, вооруженных копьями, один человек может бороться одновременно только с одним человеком. Если каждый человек убивает ровно одного (или погибает от одного) противника, то ожидаемое число воинов, оставшихся в конце сражения, — это просто разница между численностью большей и меньшей армий (при идентичности применяемого оружия).

Линейный закон применяется также к неприцельному огню по территории противника. Коэффициент убыли зависит от плотности имеющихся целей в целевой области, а также от количества стреляющих орудий. Если две группировки, занимающие одинаковую площадь и использующие одинаковые орудия, ведут огонь случайным образом по площадной цели одинакового размера, они будут убывать одинаковыми темпами до тех пор, пока меньшая группировка в конце концов не будет ликвидирована: большая вероятность поражения одним выстрелом какой-либо единицы крупной группировки уравновешивается большим числом выстрелов направленных на мелкую группировку.

Закон «честного боя» [ | ]

A 0 − A t = E ( B 0 − B t ) <\displaystyle A_<0>-A_=E(B_<0>-B_)\ >

Квадратичный закон Ланчестера [ | ]

В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.

Коэффициент убыли (rate of attrition) зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.

Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон. Заметим, что Квадратичный закон Ланчестера не относится к технологической силе, а только к численной силе, поэтому он предполагает N-квадрат-кратное увеличение качества для N-кратного увеличения количества.

Закон концентрации [ | ]

A 0 2 − A t 2 = E ( B 0 2 − B t 2 ) <\displaystyle A_<0>^<2>-A_^<2>=E(B_<0>^<2>-B_^<2>)>

(Истребительная сила) = (качество оружия) × (количество единиц) 2 <\displaystyle ^<2>>

Примечания [ | ]

Части этой статьи скопированы с разрешения из статьи Эрнеста Адамса, опубликованной на веб-сайте разработчиков компьютерных игр Gamasutra. См. ссылки ниже.

Источник

Законы Ланчестера

Законы Ланчестера (законы Осипова — Ланчестера) — математическая формула для расчета относительных сил пары сражающихся сторон — подразделений вооруженных сил. В статье «Влияние численности сражающихся сторон на их потери», опубликованной журналом «Военный сборник» в 1915 году, генерал-майор Корпуса военных топографов М. П. Осипов [1] [2] описал математическую модель глобального вооружённого противостояния, практически применяемую в военном деле при описании убыли сражающихся сторон с течением времени и, входящую в математическую теорию исследования операций, на год опередив английского математика Ф. У. Ланчестера. Мировая война, две революции в России не позволили новой власти заявить в установленном в научной среде порядке об открытии царского офицера.

Уравнения Ланчестера — это дифференциальные уравнения, описывающие зависимость между силами сражающихся сторон A и D как функцию от времени, причем функция зависит только от A и D. [3]

Содержание

Линейный закон Ланчестера

В древней битве, например между фалангами воинов, вооруженных копьями, один человек может бороться одновременно только с одним человеком. Если каждый человек убивает ровно одного (или погибает от одного) противника, то ожидаемое число воинов, оставшихся в конце сражения, — это просто разница между численностью большей и меньшей армий (при идентичности применяемого оружия).

Линейный закон применяется также к неприцельному огню по территории противника. Коэффициент убыли зависит от плотности имеющихся целей в целевой области, а также от количества стреляющих орудий. Если две группировки, занимающие одинаковую площадь и использующие одинаковые орудия, ведут огонь случайным образом по площадной цели одинакового размера, они будут убывать одинаковыми темпами до тех пор, пока меньшая группировка в конце концов не будет ликвидирована: большая вероятность поражения одним выстрелом какой-либо единицы крупной группировки уравновешивается большим числом выстрелов направленных на мелкую группировку.

Закон «честного боя»

A 0 − A t = E ( B 0 − B t ) <\displaystyle A_<0>-A_=E(B_<0>-B_)\ >

Квадратичный закон Ланчестера

В современных боевых действиях, когда боевые единицы сторон удалены друг от друга и ведут прицельный огонь, они способны поражать несколько целей, и могут поражаться с нескольких направлений.

Коэффициент убыли (rate of attrition) зависит теперь только от количества боевых единиц, ведущих огонь. Ланчестер установил, что мощность группировки в этом случае пропорциональна не количеству боевых единиц, которое она имеет, а квадрату от числа единиц. Это называется квадратичным законом Ланчестера. Точнее, закон определяет потери боевых единиц, которые сражающаяся сторона нанесет за определенный период времени, по сравнению с теми, которые нанесет противостоящая сторона.

Закон работает в предположении, что потери нарастают с течением времени: он не работает в ситуациях, в которых противостоящие войска убивают друг друга мгновенно, либо за счет одновременной стрельбы, либо если одна сторона выбывает с первого выстрела, получив большой урон. Заметим, что Квадратичный закон Ланчестера не относится к технологической силе, а только к численной силе, поэтому он предполагает N-квадрат-кратное увеличение качества для N-кратного увеличения количества.

Закон концентрации

A 0 2 − A t 2 = E ( B 0 2 − B t 2 ) <\displaystyle A_<0>^<2>-A_^<2>=E(B_<0>^<2>-B_^<2>)>

(Истребительная сила) = (качество оружия) × (количество единиц) 2 <\displaystyle ^<2>>

Примечания

Части этой статьи скопированы с разрешения из статьи Эрнеста Адамса, опубликованной на веб-сайте разработчиков компьютерных игр Gamasutra. См. ссылки ниже.

Источник