Основные понятия и определения сопромата.

Сопротивление материалов – раздел механики деформируемого твердого тела, в котором рассматриваются методы расчета элементов машин и сооружений на прочность, жесткость и устойчивость.

Прочностью называется способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций. Расчеты на прочность дают возможность определить размеры и форму деталей, выдерживающих заданную нагрузку, при наименьшей затрате материала.

Жесткостью называется способность тела сопротивляться образованию деформаций. Расчеты на жесткость гарантируют, что изменения формы и размеров тела не превзойдут допустимых норм.

Устойчивостью называется способность конструкций сопротивляться усилиям, стремящимся вывести их из состояния равновесия. Расчеты на устойчивость предотвращают внезапную потерю равновесия и искривление элементов конструкции.

Долговечность состоит в способности конструкции сохранять необходимые для эксплуатации служебные свойства в течение заранее предусмотренного срока времени.

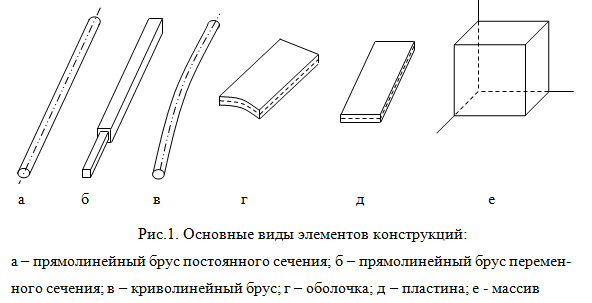
Оболочка (рис.1, г) это тело, один из размеров которого (толщина) намного меньше остальных. Если поверхность оболочки представляет собой плоскость, то объект называют пластиной (рис.1, д). Массивами называются тела, у которых все размеры одного порядка (рис.1, е). К ним относятся фундаменты сооружений, подпорные стены и др.

Эти элементы в сопротивлении материалов используются для составления расчетной схемы реального объекта и проведения ее инженерного анализа. Под расчетной схемой понимается некоторая идеализированная модель реальной конструкции, в которой отброшены все малосущественные факторы, влияющие на ее поведение под нагрузкой

Допущения о свойствах материала

Материал считается сплошным, однородным, изотропным и идеально упругим.
Сплошность – материал считается непрерывным. Однородность –физические свойства материала одинаковы во всех его точках.
Изотропность – свойства материала одинаковы по всем направлениям.
Идеальная упругость – свойство материала ( тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.

Допущения о деформациях

1. Гипотеза об отсутствии первоначальных внутренних усилий.

2. Принцип неизменности начальных размеров – деформации малы по сравнению с первоначальными размерами тела.

3. Гипотеза о линейной деформируемости тел – деформации прямо пропорциональны приложенным силам (закон Гука).

4. Принцип независимости действия сил.

5. Гипотеза плоских сечений Бернулли – плоские поперечные сечения бруса до деформации остаются плоскими и нормальными к оси бруса после деформации.

6. Принцип Сен-Венана – напряженное состояние тела на достаточном удалении от области действия локальных нагрузок очень мало зависит от детального способа их приложения

Внешние силы

Внутренние силы. Метод сечений.

Действие на тело внешних сил приводит к его деформации (меняется взаимное расположение частиц тела). Вследствие этого между частицами возникают дополнительные силы взаимодействия. Это силы сопротивления изменению формы и размеров тела под действием нагрузки, называют внутренними силами (усилиями). С увеличением нагрузки внутренние усилия возрастают. Выход из строя элемента конструкции наступает при превышении внешних сил некоторого предельного для данной конструкции уровня внутренних усилий. Поэтому оценка прочности нагруженной конструкции требует знания величины и направления возникающих внутренних усилий. Значения и направления внутренних сил в нагруженном теле определяют при заданных внешних нагрузках методом сечений.

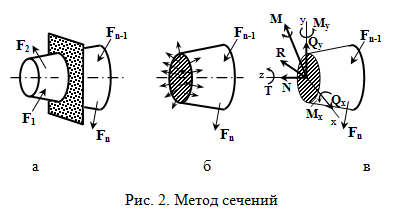
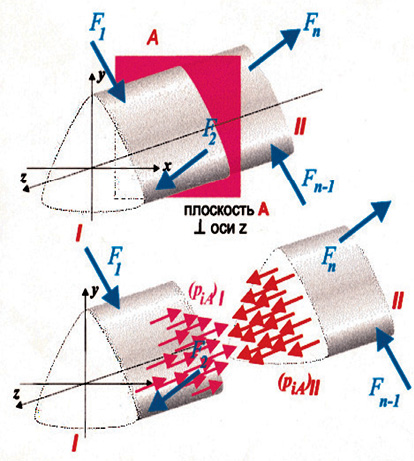
Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б). Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.

Источник

Допущения сопромата

При построении теории расчета на прочность, жесткость и устойчивость принимаются допущения, связанные со свойствами материалов и с деформацией тела.

Допущения, связанные со свойствами материалов

Сначала рассмотрим допущения, связанные со свойствами материалов :

допущение 1 : материал считается однородным (его физико-механические свойства считаются одинаковыми во всех точках;

допущение 2 : материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда). Это допущение дает возможность применять при исследовании напряженно-деформированного состояния тела методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела;

допущение 3 : материал изотропный, то есть его физико-механические свойства в каждой точке одинаковы во всех направлениях. Анизотропные материалы – физико-механические свойства которых изменяются в зависимости от направления (например, дерево);

допущение 4 : материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают).

Допущения, связанные с деформацией

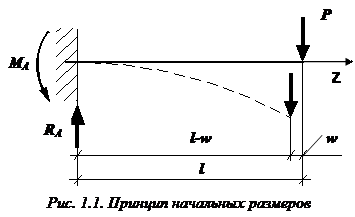
допущение 1 : деформации считаются малыми. Из этого допущения следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров. Например, рассмотрим стержень, заделанный одним концом в стену и нагруженный на свободном конце сосредоточенной силой (рис. 1.1).

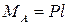
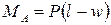
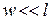
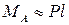
Момент в заделке, определенный из соответствующего уравнения равновесия методом теоретической механики, равен: . Однако прямолинейное положение стержня не является его положением равновесия. Под действием силы (P) стержень изогнется, и точка приложения нагрузки сместится и по вертикали, и по горизонтали. Если записать уравнение равновесия стержня для деформированного (изогнутого) состояния, то истинный момент, возникающий в заделке, окажется равным: . Принимая допущение о малости деформаций, мы полагаем, что перемещением (w) можно пренебречь по сравнению с длиной стержня (l), то есть , тогда . Допущение возможно не для всех материалов.

допущение 2 : перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (тело является линейно деформируемым). Для линейно деформируемых конструкций справедлив принцип независимости действия сил ( принцип суперпозиции ): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности. В основе этого принципа лежит также предположение об обратимости процессов нагрузки и разгрузки.

Источник

Основные гипотезы и допущения.

Реальные материалы обладают разнообразными физическими свойствами и характерной для каждого из них структурой. С целью упрощения расчетов в сопротивлении материалов используют гипотезы и допущения о свойствах материала.

Основные гипотезы и допущения:

1. Материал считается однородным, то есть его свойства во всех точках одинаковы по какому-то направлению.При изменении направления свойства могут измениться, но все равно будут одинаковы во всех точках.

2. Материал считается изотропным, то есть его свойства в произвольной точке одинаковы по всем направлениям. При переходе к другой точке свойства могут измениться, но все равно будут одинаковыми по всем направлениям.

3. Материал считается сплошным, то есть без пустот заполняет пространство, ограниченное поверхностью тела. Таким образом, материал – непрерывен, что позволяет использовать математический аппарат дифференциального и интегрального исчисления.

4. Материал считается идеально упругим, то есть полностью восстанавливает свои форму и размеры после снятия нагрузки.

5. Деформации материала прямо пропорциональны прикладываемым нагрузкам, то есть справедлив закон Гука.
Кроме того, также с целью упрощения расчетов вводятся гипотезы и допущения о схемах нагружения, действии прикладываемых нагрузок и т.д.

6. Принцип независимости действия сил. При действии на тело нескольких сил, результат действия одной части этих сил не зависит от результата действия остальных сил

Следствие: Результат действия на тело нескольких сил равен сумме результатов от действия каждой силы в отдельности и не зависит от последовательности приложения этих сил. Таким образом, одну сложную задачу можно разбить на ряд простых, а результаты «сложить».

7. Принцип начальных размеров. При составлении условий равновесия реального тела оно может считаться абсолютно твердым. То есть деформации тела под нагрузками настолько малы, что можно не учитывать изменение местоположения точек приложения нагрузок и взаиморасположения нагрузок и их линий действия между собой.

8. Гипотеза плоских сечений (Бернулли) Поперечные сечения тела, бывшие плоскими до нагружения, остаются плоскими и после нагружения.

9. Принцип Сен-Венана. Замена совокупности некоторых сил, приложенных на небольшой части поверхности тела, статически эквивалентной системой других сил не вызовет существенных изменений в условиях нагружения достаточно удаленных частей тела

Контрольные вопросы

1. Может ли тело быть «прочным», но не «жестким»? Приведите пример.

2. Приведите пример внешней активной силы и внешней реактивной силы.

3. Приведите пример динамической внешней силы.

4. Из скольких этапов состоит «метод сечений»?

5. Сформулируйте, какими свойствами обладает однородный изотропный материал.

6. Являются ли обычные металлы и сплавы (железо, чугун, сталь и т.д.) «сплошными» материалами?

Лекция 4. Центральное растяжение/сжатие прямого бруса

Определение. Примеры.

Центральным растяжением/сжатием называется такой вид нагружения бруса, при котором в любом его поперечном сечении возникают только продольные внутренние усилия.

П ример I.Какая сила действует в поперечном сечении бруса (рис.4.1)?

Для решения этой задачи применим метод сечений (РОЗУ), состоящий из нескольких этапов.

« Р»— Рассекаем брус в интересующем нас сечении (рис.4.2)

«О»— Отбрасываем одну из частей бруса

«З»-Для сохранения равновесия заменяем действие отброшенной части на оставшуюся часть бруса неизвестной пока внутренней силой

«У»-Уравновешиваем неизвестную внутреннюю силу и внешнюю нагрузку

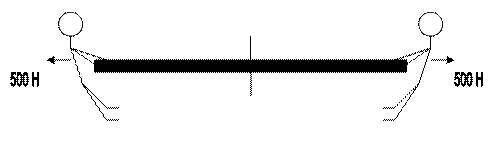
N = 500 Н

Вывод: Внутренняя сила N равна приложенной внешней нагрузке 500 Н.

Пример II.А какая сила теперь действует в сечении бруса?

Для решения снова применим метод сечений РОЗУ

Вывод: внутренняя сила N равна приложенной внешней нагрузке 500 Н

Итак: внутренняя продольная сила в рассматриваемом поперечном сечении равна сумме внешних нагрузок в оставшейся после отсечения части бруса.

Источник

Научная электронная библиотека

Лекция 1. ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Прочность, жесткость, устойчивость, – как понятия определяющие надёжность конструкций в их сопротивлении внешним воздействиям. Расчётные схемы (модели): твёрдого деформируемого тела, геометрических форм элементов конструкций. Внутренние силы в деформируемых телах и их количественные меры. Метод сечений. Напряжённое состояние. Перемещения и деформации. Понятия упругости и пластичности. Линейная упругость (закон Гука). Принцип независимости действия сил (принцип суперпозиции).

Основные понятия. Сопротивление материалов, наука о прочности (способности сопротивляться разрушению при действии сил) и деформируемости (изменении формы и размеров) элементов конструкций сооружений и деталей машин. Таким образом, данный раздел механики дает теоретические основы расчета прочности, жесткости и устойчивости инженерных конструкций.

Под нарушением прочности понимается не только разрушение конструкции, но и возникновение в ней больших пластических деформаций. Пластическая деформация – это часть деформации, которая не исчезает при разгрузке, а пластичность – способность материала сохранять деформацию.Возникновение пластических деформаций связано с нарушением нормальной работы конструкции и поэтому пластические деформации считаются недопустимым.

Жесткость – это способность конструкции (или материала) сопротивляться деформированию. Иногда деформация конструкции, отвечающей условию прочности, может воспрепятствовать нормальной ее эксплуатации. В таком случае конструкция имеет недостаточную жесткость.

Устойчивость – это способность конструкции сохранять положение равновесия, отвечающее действующей на нее нагрузке.

Конструкции, как правило, имеют сложную форму, отдельные элементы которой можно свести к простейшим типам, являющимисяосновными объектами изучения сопротивления материалов: стержни, пластинки, оболочки, массивы, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и динамических нагрузок, т.е. расчет реальной конструкции начинается с выбора расчетной схемы. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической.Стержень – тело, у которого один размер (длина) значительно превышает два других размера.

Оболочка – это тело, ограниченное двумя криволинейными поверхностями, у которого один размер (толщина) много меньше двух других размеров. Пластина – это тело, ограниченное двумя параллельными плоскостями.

Массив – тело, у которого все три размера имеют один порядок.

Базируясь на законах и выводах теоретической механики, сопротивление материалов, помимо этого, учитывает способность реальных материалов деформироваться под действием внешних сил.

При выполнении расчетов принимаются допущения, связанные со свойствами материалов и с деформацией тела.

1. Материал считается однородным (независимо от его микроструктуры физико-механические свойства считаются одинаковыми во всех точках).

2. Материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда).

3. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево).

4. Материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают, т.е. геометрические размеры тела полностью или частично восстанавливаются). Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью.

5. Деформации тела считаются малыми по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.

6. Перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (до определенной величины деформации материалов подчиняются закону Гука). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (или принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности.

7. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана.

8. Принимается гипотеза плоских сечений (гипотеза Бернулли): плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.

Внутри любого материала имеются внутренние межатомные силы. При деформации тела изменяются расстояния между его частицами, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. Для определения внутренних усилий используют метод сечения. Для этого тело мысленно рассекают плоскостью и рассматривают равновесие одной из его частей (рис. 4).

Рис. 4. Выявление внутренних усилий по методу сечений

Метод заключается в следующем:

1 Разрезаем систему (на части).

2. Отбрасываем одну часть.

3. Заменяем действие отброшенной части на оставшуюся внутренними силами упругости (приложим в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть).

4. Составляем уравнения равновесия, составленное для отсеченной части и находим значения усилий.

Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу R, равную главному вектору и пару сил с моментом M, равным главному моменту системы.

Проектируя R и M на координатные оси, получаем в общем случае 6 алгебраических величин – 6 внутренних силовых факторов:

Источник

Схематизация свойств материала

Реальные материалы обладают разнообразными физическими свойствами и характерной для каждого из них структурой. С целью упрощения расчетов в сопротивлении материалов используются следующие допущения о свойствах материала.

Изотропными являются аморфные материалы, такие как стекло и смолы. Анизотропными являются пластмассы, текстолит и т.п. Металлы являются поликристаллическими телами, состоящими из большого количества зерен, размеры которых очень малы (порядка 0,01 мм). Каждое зерно является анизотропным, но вследствие малых размеров зерен и беспорядочного их расположения металлы проявляют свойство изотропии.

4. Форма и размеры упругого тела меняются прямо пропорционально изменению нагрузок, то есть по известному закону Гука (1660 г.).

В случае чистого однородного растяжения или сжатия призматического стержня, закон Гука имеет вид:

,

,

В формулировке данной гипотезы границы применения закона пропорциональности Гука ничем не оговариваются, хотя в действительности при некоторых нагрузках начинается существенное отклонение от закона пропорциональности.

В пределах упругости имеет место эффект Пуассона (1816 г.) – отношение относительных поперечных удлинений ε / к относительным продольным удлинениям ε есть величина постоянная для данного материала»:

,

Источник