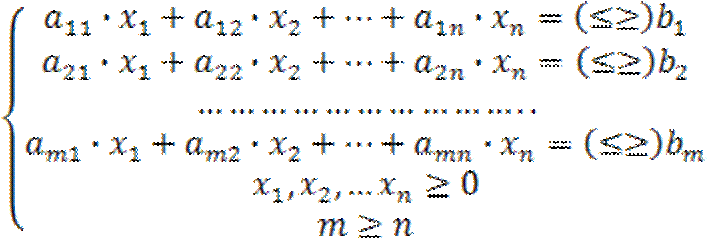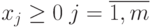в каком случае модель является оптимизационной

Оптимизация

Оптимальный — наилучший в заданных условиях. Качество оценивается с помощью критерия оптимальности, а условия задаются в виде ограничений на дополнительные критерии.

Стремление к повышению эффективности труда, творчества, любой целенаправленной деятельности, это естественное стремление человека как бы нашло свое выражение, ясную и понятную форму в идее оптимальности. Различие между строго научным и «общепринятым», житейским пониманием оптимальности совсем невелико. Правда, встречающиеся выражения типа «наиболее оптимальный» или «добьемся максимального эффекта при минимуме затрат» математически некорректны, но лица, использующие эти выражения, на самом деле просто нестрого и неудачно выражают правильную мысль: как только дело касается конкретной оптимизации, они быстро и легко исправляют формулировки.

Оптимизация — в математике, информатике и исследовании операций задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Оптимизационные модели

Оптимизационные модели предназначены для определения оптимальных (наилучших) с точки зрения некоторого критерия параметров моделируемого объекта или же для поиска оптимального (наилучшего) режима управления некоторым процессом. Часть параметров модели относят к параметрам управления, изменяя которые можно получать различные варианты наборов значений выходных параметров. Как правило, данные модели строятся с использованием одной или нескольких дескриптивных моделей и включают некоторый критерий, позволяющий сравнивать различные варианты наборов значений выходных параметров между собой с целью выбора наилучшего. На область значений входных параметров могут быть наложены ограничения в виде равенств и неравенств, связанные с особенностями рассматриваемого объекта или процесса. Целью оптимизационных моделей является поиск таких допустимых параметров управления, при которых критерий выбора достигает своего «наилучшего значения».

Оптимизационные модели исследования операций

Задача формулируется в виде математической модели. Типовая математическая модель исследования операций представлена в следующей формулировке:

Максимизация или минимизация целевой функции, при условии выполнения ограничений

Оптимальными называются решения которые по тем или другим признакам предпочтительнее других. Каждый выбор лучшего варианта конкретен, поскольку основан на соответствии установленным критериям. Говоря об оптимальном варианте, указывают эти критерии («оптимальный по…»). То, что оптимально при одном критерии, не обязательно будет таковым при другом.

Допустимое решение — если оно удовлетворяет всем ограничениям модели. Допустимых решений в отдельных случаях может быть бесконечное множество.

Оптимальное решение — если кроме того, что оно допустимо, целевая функция в этом решении достигает максимального или минимального значения.

Оптимизация — максимизация или минимизация целевой функции.

Оптимизационная модель — это модель принятия решения, содержащая показатель эффективности (целевую функцию), который необходимо оптимизировать при условии соблюдения набора заданных ограничений.

Оптимальное решение — допустимый набор значений переменных решения, оптимизирующий целевую функцию оптимизационной модели.

Модель оптимального выбора

Большое число встречающихся на практике задач выбора сводится к нахождению лучших или наиболее предпочтительных для человека вариантов, а нередко — к поиску единственно лучшего варианта. При этом у каждого лица принимающего решение (ЛПР) есть собственные субъективные представления о том, что для него является предпочтительным в конкретной ситуации выбора.

Имеется достаточно много задач, для которых можно построить математическую модель выбора, где понятие лучшего варианта формализуется путем задания одного или нескольких числовых показателей эффективности или критериев качества решения. Эти показатели, хотя и задаются ЛПР, носят объективный характер, определяемый содержанием решаемой задачи, и выражаются какими-либо функциями, зависящими от переменных, которыми измеряются свойства вариантов. В таких случаях наиболее предпочтительным для ЛПР вариантом решения задачи выбора принято считать так называемый оптимальный вариант, который соответствует экстремальному значению одного или нескольких показателей эффективности решения при существующих условиях.

Принципиальным моментом для формулировки задачи оптимального выбора является возможность описания проблемной ситуации и предпочтений ЛПР в количественной форме. Это означает, что, во-первых, возможные варианты решения (альтернативы, объекты, способы действия) определяются количественными признаками (переменными, параметрами, атрибутами), измеряемыми с помощью числовых шкал. Во-вторых, должны быть заданы количественные же показатели (критерии оптимальности, показатели эффективности, целевые функции, функции ценности), по величине которых оценивается качество выбранного варианта. Такого рода ситуации характерны для хорошо структурируемых проблем и повторяющихся ситуаций выбора, типичных для исследования операций и оптимального управления.

Для анализа возможных вариантов решения проблемы (способов достижения цели) и выбора среди них одного или нескольких лучших вариантов строятся формальные модели оптимального выбора. Модель дает упрощенное представление реальной проблемы и должна отражать наиболее важные и объективно существующие зависимости и связи между вариантами, описывающими их признаками и ограничениями, которые задаются управляемыми и неуправляемыми факторами. Построение такой модели — задача консультантов-аналитиков и экспертов при участии ЛПР. При построении модели выбора нужно соизмерять адекватность и детальность модели с точностью требуемого решения реальной задачи выбора, а также с объемом необходимой для поиска решения информации — как имеющейся в наличии, так и получаемой дополнительно.

Ограничения оптимизационного подхода

Оптимизационные проблемы являются строго формальными математическими задачами. Практическое значение решений таких задач прямо зависит от того, насколько хороша исходная математическая модель. В сложных системах математическое моделирование является затруднительным, приблизительным, неточным. Чем сложнее система, тем осторожнее следует относиться к ее оптимизации.

С позиций системного анализа отношение к оптимизации можно сформулировать следующим образом: это мощное средство повышения эффективности, но использовать его следует все более осторожно по мере возрастания сложности проблемы.

При всей очевидной полезности идеи оптимизации практика требует необходимости осторожного обращения с ней. Для такого заключения имеются достаточно веские основания.

Источник

Оптимальная или оптимизационная модель

Оптимальная или оптимизационная модель [optimization model] — экономико-математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них.

В отличие от дескриптивной (описательной, балансовой) модели оптимизационная модель содержит наряду с уравнениями, описывающими взаимосвязи между переменными, также критерий для выбора — функционал (или, что то же, целевую функцию).

Оптимизационные модели — основной инструмент экономико-математических методов. Обычно они очень сложны, насчитывают сотни и тысячи уравнений и переменных. Но общая структура таких моделей проста. Она состоит из целевой функции, способной принимать значения в пределах области, ограниченной условиями задачи (области допустимых решений), и ограничений, характеризующих эти условия. Целевая функция в самом общем виде в свою очередь состоит из трех элементов: управляемых переменных, параметров (или также переменных), которые не поддаются управлению, например, зависящих от внешней среды, и формы зависимости между ними (формы функции). Если обозначить критерий оптимальности — U (в частном случае, например, — полезность), управляемые переменные — x_i и параметры — y_i, то получим общий вид оптимизационной модели:

1) U = f (x_i, y_j) → max или min, т.е. отыскивается максимум или минимум функции f (x, y) в зависимости от того, какой показатель выбран в качестве критерия;

Полезное

Смотреть что такое «Оптимальная или оптимизационная модель» в других словарях:

Оптимизационная модель — См. Оптимальная (или оптимизационная) модель … Экономико-математический словарь

оптимальная модель — оптимизационная модель Экономико математическая модель, которая охватывает некоторое число вариантов (технологических способов) производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти… … Справочник технического переводчика

Экономико-математическая модель — [economic model, eco­no­mico mathematical model] математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи (поэтому часто термины… … Экономико-математический словарь

экономико-математическая модель — Математическое описание экономического процесса или объекта, произведенное в целях их исследования и управления ими: математическая запись решаемой экономической задачи (поэтому часто термины “модель” и “задача” употребляются как синонимы).… … Справочник технического переводчика

О — Обеспечение кредита (Security for credit, loan security, collateral) Обеспеченность производства запасами (number of days’, weeks’ stock) Обесценение активов (impairment of assets) … Экономико-математический словарь

Источник

Оптимизационные модели в экономике. Способы нахождения оптимальных решений

Оптимизационные модели – это социально-экономические модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребленияи др.

Данные модели основаны на математическом аппарате теории программирования(«планирование»). Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование(ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:

1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X = (x₁,x₂. x_n ). В качестве показателя оптимальности часто выступают экономические показатели: выручка, себестоимость, прибыль и пр.;

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Ограничения в экономических задачах могут быть по спросу, по запасам ресурсов, по трудоемкости, по затратам времени и пр.

Целевая функция (ЦФ)

Основные правилапостроение оптимизационной модели: число ограничений (m) должно быть больше либо равно числу искомых переменных x; в ограничения левая и правая части должны иметь одинаковые единицы измерения.

Допустимое решение– это совокупность чисел (план) X = (x₁, x₂, … x_n), удовлетворяющих ограничениям задачи. Оптимальное решение –это план, при котором ЦФ принимает свое максимальное (минимальное) значение.

В случае, если количество искомых величин х две, то удобно решение задачи представить в графической форме.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (x₁,x₂) некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений(ОДР). ОДР всегда представляет собой выпуклуюфигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

Оптимальной считается точка, через которую проходит линия уровня Lmax (Lmin), соответствующая наибольшему (наименьшему) значению функции L(X). Оптимальное решение всегда находится на границе ОДР. При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

В случае, если количество искомых величин х более двух, то применяют метод перебора всех возможных вариантов с помощью ЭВМ (в Excel это надстройка «Поиск решения»).

На основе оптимизационных моделей были созданы различные вариации экономических задач:

— задача о размещении (транспортная задача)– это задача линейного программирования (ЛП), в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.Для решения транспортных задач применяются метод северо-западного угла и метод Фогеля.

— распределительная задача ЛП –это РЗ, в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.

Источник

Оптимизационные модели

4.1. Постановка оптимизационной задачи

Принятию любого экономического или финансового решения предшествует перебор и оценка вариантов. Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными [18, 19].

Типы оптимизационных задач в экономике:

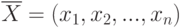
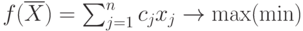
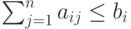В общем виде задача линейного программирования ЗЛП ставится следующим образом: найти вектор , максимизирующий (минимизирующий) линейную форму , удовлетворяющий условиям:

( 4.1)

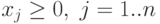( 4.2)

где — заданная функции, — некоторые действительные числа.

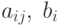
Приведем примеры экономико-математического моделирования оптимизационных задач средствами Mathcad.

4.2.Оптимальное планирование выпуска продукции

Определение переменных. Введем обозначения:

–видов продукции, – текущий номер вида продукции.

— прибыль от реализации единицы -го вида продукции.

— переменные затраты производства единицы -го вида продукции

— запасы -го ресурса – текущий номер вида ресурса, — количество ресурсов.

— норма затрат го ресурса для производства -го вида продукции

– требуемое количество выпуска продукции каждого вида по плану,

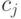
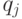
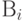
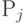
Выходные показатели – суммарная прибыль ,

Управляемые переменные. — искомый объем продукции -го вида.

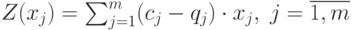( 4.3)

( 4.4)

Ограничения. условия, налагаемые на данные задачи, определяющие исследуемую величину, которая оптимизируется. Различают три типа ограничений:

– планируемые затраты ресурса для производства продукции ,

– планируемые затраты ресурса на производство всех видов продукции,

— условие ограниченности ресурсов

— условие ограниченности по плану

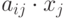
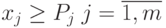
технологические соотношения между группами управляемых переменных, здесь

Уравнения. В результате имеем систему уравнений, которую надо решить.

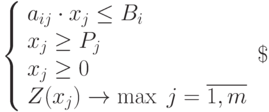( 4.5)

Решение, если получено, представляется в виде оптимального решения. Это:

количество управляемых переменных, не равных нулю,

числовые значения управляемых переменных,

полученное значение целевой функции

Рассмотрим решение модели на примере следующей задачи.

Источник

Оптимизационные модели

Нестеров А.К. Оптимизационные модели // Энциклопедия Нестеровых

Понятие оптимизационных моделей

Экономико-математические задачи, преследующие цель определить оптимальный вариант использования имеющихся ресурсов при соблюдении определенных условий, относят к разряду оптимизационных. Такие задачи решаются с помощью оптимизационных моделей. Структура оптимизационных моделей состоит из целевой функции, множества допустимых решений и заданной системы ограничений, которые определяют область возможных решений.

Целевая функция оптимизационной модели включает в себя управляемые переменные, неуправляемые переменные и формы функции.

Множество допустимых решений – это область возможных вариантов решения оптимизационной задачи, в пределах которой осуществляется выбор решений.

Заданная система ограничений в экономических задачах представляется имеющимися в наличии ресурсами и условиями их возможного использования в целях решения оптимизационной задачи. Система ограничений формализуется в виде уравнений и неравенств. Ограничения в оптимизационных моделях могут быть линейными и нелинейными, детерминированными и стохастическими.

Задачи построения оптимизационных моделей

Основная задача построения оптимизационных моделей заключается в нахождении экстремума функций при заданных ограничениях в виде систем уравнений и неравенств. Учитывая, что в рамках современных экономических систем большинство процессов являются массовыми и описываются сложными закономерностями, построение оптимизационных моделей позволяет охарактеризовать любой процесс с помощью математических уравнений и рационального подхода к моделированию.

Оптимизационные модели предназначены для выявления наилучшего решения при соблюдении заранее заданных, определенных и конкретизированных условий и ограничений. Оптимизационная модель описывается с помощью целевой функции, имеющей много аргументов. В ходе оптимизации с помощью сконструированной функции перебирается все множество значений аргументов поочередно до тех пор, пока значение функции станет удовлетворять поставленным условиям в рамках оптимизационной модели. В оптимизационную модель должен обязательно входить один или несколько параметров, на которые можно оказывать влияние, чтобы добиться соблюдения условиям оптимума при наличии определенных ограничений.

Оптимизационные модели позволяют посредством анализа совокупности альтернативных вариантов решений определить наилучший вариант производства, распределения или потребления в условиях ограниченности имеющихся ресурсов, которые будут использованы наиболее эффективным образом для достижения поставленной цели, что является экономическим содержанием данных моделей.

В оптимизационных моделях объектом моделирования может выступать:

Анализ ситуации, составляющей основу оптимизационной модели, сводится к оценке функционирования объекта моделирования, например, оптимизация работы склада предприятия должна учитывать скорость сбыта готовой продукции, размеры склада, объем оборотных средств. В зависимости от оптимизационной модели ненаблюдюдаемые параметры, включающие целевые значения функции и основных переменных, должны быть определены таким образом, чтобы обеспечить возможность рационального и обоснованного управления экономическими процессами. В то же время наблюдаемые параметры, которые сводятся к совокупности условий и ограничений, создают граничные условия для искомых значений функции.

Адекватность оптимизационной модели должна быть обеспечена таким образом, чтобы полностью или практически полностью характеризовать действительное функционирование объекта моделирования. Математический аппарат оптимизационной модели должен соответствовать описанию конкретного экономического процесса, например, отражать аналитические связи между основными параметрами функционирования склада готовой продукции на предприятии.

Это позволяет обеспечить достоверный анализ результатов моделирования выбранного объекта, которому подвергается совокупность всех оптимальных значений основных переменных и целевой функции, найденных в ходе перебора значений аргументов. На основе результатов такого анализа могут быть сделаны соответствующие выводы, благодаря которым принимается обоснованное оптимальное решение по управлению экономическим объектом или отдельным процессом.

Таким образом, следует сделать вывод:

Оптимизационные модели не являются единственным источником знаний о конкретном объекте, напротив, моделирование составляет более обширный и глубокий процесс познания особенностей функционирования объекта. Этот факт учитывается не только в рамках построения модели, но и при интерпретации полученных результатов, которые могут быть применены к объекту моделирования.

Элементы оптимизационной модели

Построение оптимизационной модели предваряет определение ее элементов. К обязательным элементам оптимизационной модели относятся переменные параметры конкретного экономического процесса, ограничения задачи и критерий оптимальности.

Элементы оптимизационной модели

Описание элементов оптимизационной модели приведено в таблице.

Элемент оптимизационной модели

Переменные параметры процесса

Переменные параметры процесса представляют собой совокупность неизвестных величин, значения которых определяются в ходе решения оптимизационной задачи и используются для рационального функционирования экономического процесса. Ограничения задачи – это символическая запись обязательных условий организации данного экономического процесса в виде неравенств и уравнений, что в целом соответствует системе ограничений в структуре оптимизационной модели. Критерий оптимальности является конкретным экономическим показателем, экстремум которого соответствует наиболее эффективной оптимизации экономического процесса.

Ограничения оптимизационной задачи

Правильное определение ограничений оптимизационной задачи является важным условием адекватной модели, вместе с тем необходимо избегать чрезмерного усложнения модели, что затруднит подготовку данных, процесс решения и анализ полученных результатов. С другой стороны нельзя допускать слишком упрощенной реализации модели, что неизбежно приведет к получению неадекватной модели, несоответствующей реальному экономическому процессу. Рациональные ограничения задачи могут включать в себя условия по объему производства и используемых ресурсов, балансовые соотношения между переменными, специальные условия для отдельных контрагентов предприятия, а также условия типизации и стандартизации производственных процессов в рамках оптимизационной модели.

Критерий оптимальности должен соответствовать следующим базовым требованиям. Во-первых, должно обеспечиваться глобальному критерию, с которым связано решение оптимизационной задачи. Во-вторых, необходим учет экономических последствий принимаемых решений, сформированных на основе результатов решения оптимизационной задачи. В-третьих, требуется исключение одинаковых по величине издержек. В-четвертых, следует учитывать текущую экономическую ситуацию в отношении хозяйствующего объекта, объекта моделирования.

Примеры применения оптимизационных моделей

К примеру, если предприятие выпускает редкую продукцию, пользующуюся относительно высоким спросом, то целью оптимизационной задачи будет максимально увеличить объем производства этой продукции, а критерием оптимальности оптимизационной модели будет выступать максимальный выпуск продукции с единицы производственной мощности.

В качестве другого примера можно привести ситуацию, когда производственные мощности предприятия полностью загружены и их достаточно для производства такого объема продукции, который полностью удовлетворяет потребность в ней, то целью оптимизационной задачи может выступать наиболее эффективный вариант организации производства, а критерием оптимальности – получаемая предприятием прибыль.

В случае, когда объем производства на предприятии не может меняться, в качестве цели оптимизационной задачи может быть определено снижение себестоимости производства, а критерием оптимальности может выступать уровень издержек в стоимостном выражении или минимальный расход какого-либо дорогостоящего сырья.

Этапы построения оптимизационных моделей

Содержание этапа построения оптимизационной модели

Постановка проблемы и ее качественный анализ

Первым этапом построения оптимизационных моделей является постановка экономической проблемы и её качественный анализ. На данном этапе необходимо определить суть проблемы, допущения и основные вопросы оптимизационной задачи. Также данный этап включает описание моделируемого объекта, его структуры, имеющих место зависимостей и аналитических связей, формирование предварительных гипотез, объясняющих дальнейшее развитие объекта.

Построение математической модели

Вторым этапом является построение математической модели, которое представляет собой формализацию экономической проблемы в виде конкретных математических зависимостей, функций, уравнений, неравенств и т.д. В рамках данного этапа также определяется конкретный перечень переменных, условий, дополнительных параметров и характер связей.

Математический анализ модели

Третий этап представляет собой математический анализ модели. На данном этапе производится исследование общих свойств модели с помощью математических приемов и доказывается существование решений в рамках сформулированной модели. В случае, если доказано отсутствие решений, то дальнейшая работа в рамках данной модели бессмысленна, следует произвести коррекцию постановки оптимизационной задачи либо ее математической формализации. На данном этапе выясняются также такие вопросы, как, например, единственно ли решение, какие переменные могут входить в решение, пределы их изменений, тенденции этих изменений, а также какие могут быть соотношения между этими переменными. Аналитические выводы, сделанные на данном этапе, сохраняют свое значение при любых значениях параметров оптимизационной модели в отличие от эмпирических выводом, которые справедливы только для конкретных значений переменных.

Подготовка исходной информации

На четвертом этапе производится подготовка исходной информации. В этих целях используются методы теории вероятностей и статистический сбор данных. При этом затраты на сбор информации не должны превышать эффект от получения дополнительной информации в результате решения оптимизационной задачи.

Разработка алгоритмов для численного решения оптимизационной задачи

Пятый этап включает в себя разработку алгоритмов для численного решения оптимизационной задачи, а также производится подбор необходимого программного обеспечения. Основной целью данного этапа является непосредственная расчетная работа. Объем экономических задач и учитываемой информации обуславливает основные трудности данного этапа. Численное решение оптимизационной задачи имеет многовариантный характер, существенно дополняет результаты, полученные в рамках математического анализа модели. Следует отметить, что для сложных экономических процессов численное решение является единственно осуществимым, поскольку перечень экономических задач, которые решаются численными методами, значительно превышает число экономических задач, доступных для аналитического исследования.

Анализ численных результатов и их применение

Шестым этапом является анализ численных результатов и их применение. На этом заключительном этапе построения оптимизационной модели оценивается достоверность, адекватность и объективность результатов моделирования, делается вывод о возможности их практического применения.

Вывод

Оптимизационные задачи можно рассматривать как простые математические модели принятия управленческих решений в рамках системы планирования и управления хозяйственной деятельностью предприятия. Оптимизационные модели наиболее часто используются в практике хозяйствующих субъектов для максимизации прибыли на предприятии или отдельных направлениях деятельности, для сокращения расходов на производство и минимизации убытков, которые могут понести предприятия вследствие наступления определенных рисковых событий. Вместе с тем, оптимизационные модели позволяют усовершенствовать систему экономической информации на предприятии, интенсифицировать экономические расчеты и повысить их точность, увеличить глубину и эффективность количественного анализа экономических проблем, а также предоставляют возможности решать принципиально новые экономические задачи.

Источник