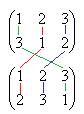
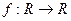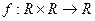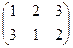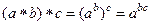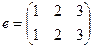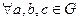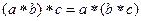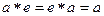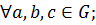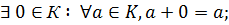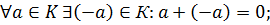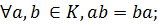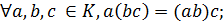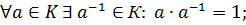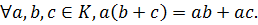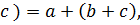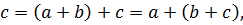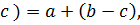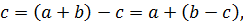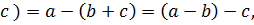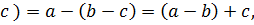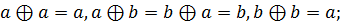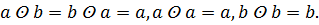в каком случае можно сказать задана бинарная алгебраическая операция на множестве или нет

Бинарные алгебраические операции.

Взаимосвязь между матанализом и алгеброй.

В матанализе изучаются, в частности, функции одного и двух аргументов.

Пример 1. 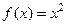, т.е.

Пример 2. 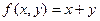, здесь

Впрочем, верхняя строка информации не несёт, можно писать только 2-ю строку, это называется перестановкой. Пример: (3 1 2).

Перестановок 2 порядка всего две: (1 2) и (2 1).

Перестановки 3 порядка:

(1 2 3), (1 3 2) (2 1 3), (2 3 1) (3 1 2), (3 2 1).

Их всего 6. Чтобы перечислить их все, можно на 1 месте поставить число, а на двух других остаётся по 2 варианта расположить оставшиеся 2 числа.

Лемма. Существует n! перестановок порядка n.

Доказательство.

Для n = 2 это очевидно, перестановки только (12) и (21).

Дальше, доказательство по индукции. Пусть теперь для (n-1) этот факт доказан. Рассмотрим для n. На первом месте может стоять любое из n чисел, и при каждой из этих ситуаций, остаётся (n-1) число, которые должны занять (n-1) место, а это возможно (n-1)! способами. Итак, получается 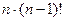что как раз равно n!, что и требовалось доказать.

В частности, при n = 3 получается 6 перестановок:

(123) (132) (213) (231) (312) (321)

На первом месте одно из 3 чисел, и при этом оставшиеся 2 числа можно расставить на 2 места двумя способами. Получается 6 способов. Заметим, что 3! = 6.

Назовём инверсией такую ситуацию, когда большее число в перестановке расположено раньше, чем меньшее. В перестановке (12) инверсий нет, количество инверсий 0, то есть чётно. В перестановке (21) одна инверсия (то есть, их количество нечётно).

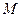
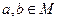
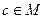
Определение 1. На множестве задана бинарная алгебраическая операция, если каждой паре элементов поставлен в соответствие однозначно определённый элемент .

Примечание. Результат операции также принадлежит М, другими словами, множество замкнуто относительно этой операции.

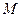
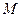
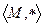
Определение 2. Если на задана бинарная алгебраическая операция, то называется группоидом, и обозначается .

Примеры.

2. Множество целых чисел с операцией умножения. 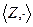. Аналогично прошлому примеру, является группоидом.

3. , где является группоидом. Положительная степень натурального числа есть снова натуральное число.

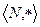
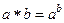
Не является группоидом, так как эта операция может привести к тому, что результат не принадлежит данному множеству, например, если .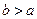

Свойства операций.

1. 2. 3. 4. коммутативные группоиды.

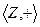
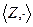
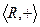
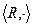
5. , где . Не коммутативный группоид. Как минимум, , есть и много других примеров.

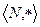
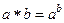
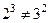
1. 2. 3. 4. ассоциативные группоиды.

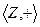
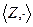
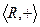
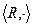
5. , где . Не ассоциативный группоид.

, так как в общем случае .

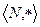
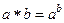
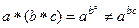
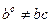
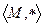
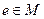
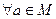
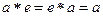
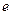
Пусть дан группоид . Если существует такой элемент , что выполняется , то называется нейтральным элементом этого группоида.

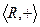
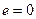
Пример 1. операция сложения, тогда .

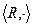
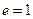
Пример 2. операция умножения, тогда .

Нейтральный элемент существует не всегда.

Пример 3. Векторное умножение в пространстве. Если каждой паре векторов ставится в соответствие их общий перпендикуляр, то результат действия операции перпендикулярен каждому из векторов, и невозможна ситуация .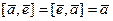

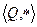
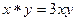
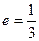
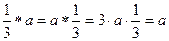
Пример 4. , операция . Тогда . .

Лемма. Если существует нейтральный элемент, то он единственный.

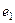
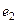
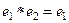
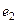
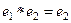
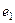
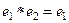
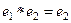
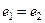
Доказательство. Допустим, что существует 2 нейтральных элемента, и . Если мы умножим их между собой, то должно быть во-первых , так как нейтральный, но во-вторых, тогда , так как тоже нейтральный. Получается

, , то есть .

Симметричный (обратный) элемент

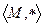
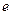
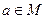
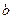
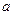
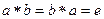
Определение. Пусть группоид содержит нейтральный элемент . Элемент . Элемент называется симметричным относительно , если .

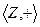
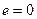
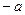
1. При сложении, в , нейтральный , симметричный это противоположный элемент .

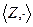
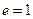
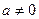
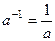
2. При умножении, в , нейтральный , симметричный это обратный элемент: для существует .

3. , операция . . Обратный равен , так как .

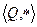
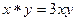
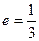
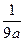
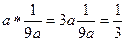
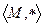
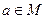
Лемма. Пусть полугруппа (т.е. операция ассоциативна). Тогда, если для элемента существует симметричный, то он единственный.

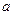
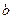
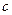
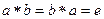
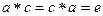
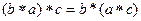
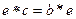
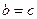
Доказательство. Пусть для существует 2 разных симметричных элемента, и . Тогда

, . Рассмотрим равенство , из него следует, что , но тогда .

Пример. Подстановки, нейтральный

Группы

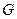
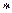
Определение. Множество с заданной на нём бинарной операцией называется группой, если:

1) выполняется ассоциативность, т.е.

2) существует нейтральный элемент 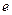, то есть

3) существует симметричный (обратный) , т.е. .

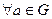
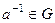
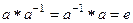
Примеры.

, , — «аддитивные» группы (по сложению).

, — «мультипликативные» группы (по умножению).

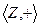
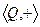
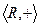
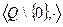
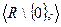
Если операция коммутативна, то группа называется коммутативной, или абелевой.

Определение подгруппы.

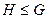
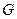
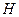
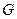
Непустое подмножество группы называется подгруппой, если само является группой относительно операции, введённой в группе .

Примеры.

1) сама группа есть подгруппа, .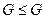

2) множество, состоящее только из нейтрального элемента, .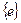

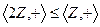
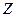
Пример. , все чётные числа. 0 нейтральный как в самой , так и в подгруппе.

Впрочем, подгруппой является любое подмножество вида .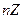

Пример. Подмножество 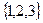подгруппой не является, т.к. результат сложения может быть и больше 3, т.е. выводит за пределы этого множества.

Примеры.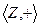

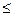
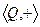
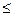
Пример. Конечная группа, дана таблица умножения элементов:

Похоже на то, что было при изучении подстановок, только не унарная, а бинарная операция. Есть 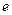, это 1. Для каждого есть обратный. Для 2 это 3, для 3 это 2. В каждой строке (и каждом столбце) перестановка из трёх различных чисел.

Источник

Свойства бинарной алгебраической операции

АЛГЕБРА

(ЧАСТЬ 1)

Материалы для практических занятий

и самостоятельной работы

для студентов факультета МиИТ

Кафедра: «Алгебры, геометрии и методики преподавания

(направления 010100.62 «Математика»; 050100.62)

Составили: канд. физ.-мат. наук О.Н. Шатных.

Утверждены на заседании кафедры «19» ноября 2013 г.

Рекомендованы методическим советом университета

1 Понятие бинарной алгебраической операции…………………………………. 5

2 Свойства бинарной алгебраической операции…………………………………..5

Тема 2 Поле комплексных чисел………………………………………………….10

1 Алгебраическая форма комплексного числа…………………………………. 11

2 Геометрическая форма комплексного числа…………………………………. 13

3 Тригонометрическая форма комплексного числа……………………………. 14

3.1 Умножение и деление комплексных чисел, записанных в тригонометрической форме………………………………………………………..15

3.3 Извлечение корней n-ой степени из комплексного числа…………………. 15

5 Геометрическое решение уравнений……………………………………………18

Раздел 2 Матрицы и определители………………………………. 19

Тема 1 Матрицы. Определение матрицы, виды матриц, действия над матрицами.…………………………………………………….……………………19

Тема 2 Определители. Перестановки из n элементов. Подстановки n-ой степени. Определение определителя n-го порядка. Свойства определителей. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки или столбца. Следствие из неё……………..……………………………. 23

Тема 3 Обратная матрица. Вырожденные и невырожденные матрицы. Обратная матрица и ее вычисление. Матричные уравнения……………………………….27

Раздел 3 Системы линейных уравнений. Методы решения систем линейных уравнений…………………………………………………………………………. 29

Тема 1 Решение системы n – линейных уравнений с n неизвестными в матричном виде…………………………………………………………………….29

Тема 3 Метод последовательного исключения неизвестных (метод Гаусса). 33

Настоящие материалы составлены в соответствии с программой дисциплины «Алгебра» и предназначены для студентов направлений «Математика» и «Педагогическое образование» профиля «Математическое образование».

Разделы «Алгебры», «Поле комплексных чисел», «Матрицы и определители», «Системы линейных уравнений» изучаются в первом семестре. В данной брошюре представлены все темы раздела, которые выносятся на практические занятия. Для каждой темы указаны основные теоретические положения, приведены образцы решения типовых задач и список задач для решения.

Раздел 1 Алгебры

Тема 1 Понятие алгебры

Понятие бинарной алгебраической операции

Определение. Бинарной алгебраической операцией на множестве М называется правило (закон), по которому любым двум элементам из М, взятым в определенном порядке (т.е. паре (а,b)), ставится в соответствие единственный элемент с из этого же множества.

Пример. 1 Операция сложения на множестве чисел N, Z, Q, R.

2 Операция умножения на множестве чисел N, Z, Q, R.

Задачи для решения

1 Какие из арифметических действий (сложение, вычитание, умножение, деление) являются бинарными операциями:

2 Является ли бинарной операцией:

а) умножение на множестве иррациональных чисел;

б) сложение на множестве четных чисел;

в) сложение на множестве нечетных чисел;

г) нахождение десятичных логарифмов на множестве ;

д) нахождение среднего геометрического двух чисел на множестве ;

е) нахождение наибольшего общего делителя на множестве N?

3 Являются ли действия, выполняемые по формулам:

б) a ◦ b=

в) a ◦ b =

бинарными операциями на множестве Q, и если являются, то почему?

4 Являются ли алгебраической системой множество чисел вида относительно: а) сложения; б) вычитания; в) умножения?

5 Является ли алгебраической системой множество радиусов-векторов, исходящих из начала декартовой системы координат и расположенных в первой четверти координатной плоскости, с операцией: а) сложение векторов; б) вычитание векторов?

Свойства бинарной алгебраической операции

Определение. Операция ◦ на множестве М называется коммутативной, если для любых а и b из этого множества справедливо равенство

Определение. Операция ◦ на множестве М называется ассоциативной, если для любых а, b, c M справедливо равенство

Определение. Пусть на М задана операция ◦. Элемент е называется нейтральным относительно операции ◦, если для любого а 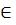М справедливо равенство

Определение. Пусть на М задана операция ◦. Элемент аʹ называется симметричным к элементу а относительно операции ◦, если выполняется равенство

По сложению, аʹ обозначают –а и называют противоположным. По умножению, аʹ обозначают и называют обратным.

Определение. Пусть на М задана операция ◦. Операция ◦ называется обратимой, если для любых а, b M уравнения а ◦ x = b, y ◦ a = b имеют решение, причем единственное.

Пусть дано множество, на котором выполнимы две операции ◦ и *.

Определение. Операция ◦ называется дистрибутивной относительно операции *, если для любых a, b, c 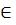M выполняются равенства

Пример 1 Докажем, что на множестве R бинарная операция, заданная формулой a ◦ b = коммутативна, но не ассоциативна.

Решение. Пусть a, b, c – любые действительные числа. В силу коммутативности сложения на R получим:

a ◦ b = b ◦ a,

т.е. бинарная операция нахождения среднего арифметического на R коммутативна. Далее,

(a ◦ b) ◦ c = 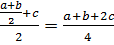(1)

a ◦ (b ◦ c) = (2)

Из результатов (1) и (2) следует, что при а ≠ с равенство (a ◦ b) ◦ c=a◦(b ◦ c) не является справедливым. Следовательно, заданная операция не ассоциативна на R.

Пример 2 Докажем, что во множестве К, содержащем не менее двух элементов, на котором формулой a ◦ b = b задана бинарная операция, не существует нейтрального элемента.

Допустим, что в К существует нейтральный элемент е, и пусть а – любой элемент из К. По определению нейтрального элемента а◦ е = а, а из условия примера следует, что а◦ е = е, т.е. а = е. Это означает, что К состоит из одного элемента. Полученный результат противоречит условию, а потому сделанное допущение ошибочно.

Задачи для решения

1 Являются ли коммутативными и ассоциативными на множестве Z бинарные операции сложения, умножения и вычитания?

2 Докажите, что на множестве бинарная операция а ◦ b = нахождения среднего геометрического коммутативна, но не ассоциативна.

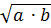
4 Какие из нижеприведенных бинарных операций:

а) a ◦ b = ;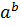

б) a ◦ b = c, где с – наибольший общий делитель чисел а и b;

в) a ◦ b = m, где m – наименьшее общее кратное чисел а и b, коммутативны и какие ассоциативны на множестве N.

5 Покажите, что действие выполняемое по правилу a ◦ b = , является коммутативной, но не ассоциативной бинарной операцией на множестве R.

6 Докажите, что относительно обычного умножения множество А= x=3k, k Z> не содержит нейтрального элемента. Обратима ли операция умножения на множестве А?

7 Пусть I – множество подмножеств некоторого непустого множества М. Существует ли в I нейтральный элемент (если существует, то какой) относительно операции объединения подмножеств на I; пересечения подмножеств? Какие элементы множества I имеют симметричные относительно операций объединения и пересечения? Обратимы ли указанные операции на множестве I?

8 Докажите, что на множестве Q действие, выполняемое по правилу a◦b = = 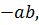является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система нейтральным элементом, и если обладает, то каким именно?

Виды алгебр

Определение. Алгеброй называется любое непустое множество А, на котором задана некоторая система операций

Обозначается (А, S), где А – множество, S – система операций.

Определение. Непустое множество М называется полугруппой, если в нем выполнима одна бинарная алгебраическая операция, которая является ассоциативной.

Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция ◦, которая обладает свойствами:

1) ◦ ( b ◦ c ) = ( ◦ b ) ◦ c,

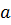
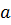
2) ◦ e = e ◦ = ;

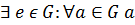
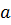
3) ◦ ʹ = ʹ ◦ = e.

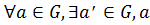
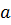
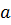
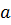
Группы по сложению называются аддитивными; группы по умножению – мультипликативными.

Определение. Непустое множество G называется группой, если в этом множестве выполнима одна бинарная алгебраическая операция, которая является ассоциативной и обратимой.

Определение. Если в группе G операция коммутативна, то группа G называется абелевой.

Определение. Непустое множество К называется кольцом, если в нем выполнимы две бинарные алгебраические операции – сложение и умножение, удовлетворяющие условиям:

1)

2)

3)

4)

5)

Примеры колец. При обычных операциях сложения и умножения кольцом является множество целых чисел, множество рациональных чисел, множество действительных чисел.

Определение. Непустое множество Р называется полем, если в нем выполнимы две бинарные алгебраические операции сложение и умножение, удовлетворяющие аксиомам:

1)

2)

3)

4)

5)

6)

7)

8)

9)

Пример 1 Доказать, что на множество Z образует группу относительно действия, заданного формулой

◦

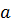
1 Рассматриваемое на Z действие сводится к сложению или вычитанию целых чисел, а т.к. сложение и вычитание элементов из Z дает в результате элемент из Z, то на множестве Z рассматриваемое действие является бинарной операцией.

2 Проанализируем возможные случаи

a) Если a, b – четные числа, а с – любое число из Z, то

◦ ◦

◦ ) ◦

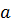
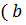
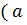
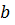
т.е. ◦ ◦ ◦ ) ◦ .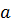

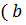
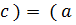
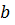
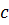
б) Если a – четное число, b – нечетное, а с – любое число из Z, то

◦ ◦

◦ ) ◦

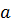
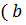
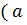
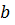
т.е. ◦ ◦ ◦ ) ◦ .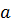

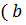
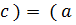
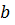
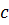
в) Если a – нечетное число, b – четное, а с – любое число из Z, то нечетно и потому

◦ ◦

◦ ) ◦

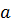
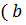
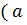
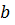
т.е. ◦ ◦ ◦ ) ◦ .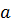

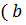
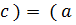
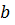
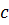
г) Если a, b – нечетные числа, а с – любое число из Z, то четно и потому

◦ ◦

◦ ) ◦

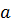
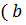
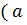
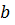
т.е. ◦ ◦ ◦ ) ◦ .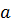

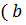
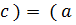
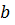
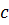
Итак, во всех возможных случаях заданная на Z бинарная операция является ассоциативной.

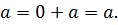
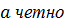
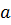
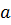
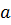
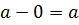
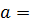
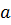
3 Т.к. 0 – четное число, то 0 ◦ Кроме того, если , то ◦ 0 = если же нечетно, то ◦ 0 = . Итак, 0 ◦ ◦ 0, т.е. 0 является в Z нейтральным элементом относительно заданной операции.

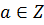
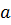
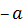
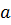
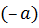
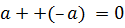
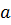
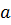
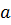
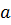
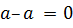
4 Для любого элемента в Z существует обратный элемент: для четного обратным будет противоположное число , т.к. ◦ = ; для нечетного обратным будет само число , т.к. ◦ = .

Итак, Z является группой относительно заданной операции.

Задачи для решения

1 Является ли множество Z полугруппой относительно: а) сложения, б) вычитания?

2 Является ли множество N полугруппой относительно операции нахождения наибольшего общего делителя?

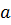
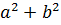
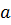
3 Почему множество R не является полугруппой относительно действия, выполняемого по правилу ◦ b = для любых , b

4 Выясните, какие из нижеприведенных множеств являются группами относительно нижеуказанных операций:

а) множество Z относительно вычитания;

б) множество четных чисел относительно умножения;

в) множество целых чисел, кратных любому заданному натуральному числу n, относительно сложения;

г) множество 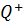относительно умножения;

д) множество Q относительно умножения;

е) множество Q \ <0>относительно умножения;

ж) множество R \ <0>относительно умножения;

з) множество трехмерных (n-мерных) арифметических векторов относительно сложения;

и) множество чисел вида а + b относительно сложения, если а и b – любые рациональные числа;

к) множество многочленов одной и той же степени n от одного аргумента относительно сложения;

л) множество многочленов степени не выше n относительно сложения;

м) множество многочленов от одного аргумента относительно сложения;

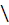
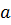
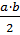
5 На множестве Q <0>определено действие ◦ b = . Докажите, что относительно указанного действия данное множество является группой.

6 Является ли кольцом множество L чисел вида относительно обычных операций сложения и умножения?

8 Докажите, что множество А чисел вида 2а + 2b 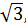где a, b – любые целые числа, является числовым кольцом.

9 Для каких чисел n = 2, 3, 4, 5, 6, 7 существует поле из n элементов?

10 Почему кольцо <0>не является полем?

11 На множестве М = сложение и умножение определены следующим образом:

Выясните, обладает ли это множество нулем и единицей и является ли система полем относительно заданных бинарных операций.

Источник