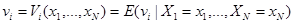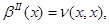в каком случае нарушается эквивалентность стратегий при выборе структуры аукциона

Математика аукционов. Лекция в Яндексе

Аукционы используются для торгов практически любых товаров — рыбы и цветов, лицензий на 3G-cвязь, государственных ценных бумаг, акций частных компаний, рекламных объявлений на Яндексе. Базовые правила некоторых аукционов остаются неизменными на протяжении столетий. При этом аукционы — динамично развивающаяся область современной экономической теории. Это в первую очередь вызвано их практической важностью, а также наличием данных и возможностью формально проанализировать аукционы как игры, чьи правила совпадают с практикой. За исследование аукционов и в целом экономических механизмов было присуждено несколько Нобелевских премий.

В рамках Малой Школы анализа данных лекцию, посвященную аукционам, прочитал Сергей Измалков — профессор экономики Российской экономической школы, председатель ученого совета РЭШ. Именно аукционы стали темой его докторской диссертации. В лекции Сергей Борисович рассказывает о том, чем похожи торговля жёнами в Вавилоне и размещение рекламных объявлений в интернете. Под катом вы найдете текстовую версию лекции, но мы бы рекомендовали вам все же посмотреть видеозапись — лектор рассказывает обо всем достаточно доступно и очень увлекательно.

Аукцион – это способ (процедура) продажи товара, может быть, покупки товара. Аукцион обычно имеет явные правила. Например, я посмотрю на поступившие предложения, выберу наилучшее и по этому лучшему предложению продам – это явное правило игры. В жизни эти правила не всегда явно сформулированы, например, в той ситуации, когда вы говорите с одним продавцом, но ждете, что, возможно, придет еще кто-то и сделает лучшее предложение. И вы начнете разговор с новым продавцом или скажете старому: вот, мол, появился новый покупатель, так что, если желаете выиграть, не хотите ли повысить свое предложение? В конце концов все это направлено на то, чтобы совершить сделку. Какие у аукционов, как правил игры, как правил продажи, могут быть цели? Цели: чтобы это произошло быстро и просто; и еще необходимо определить, по какой цене и кто купит.

Как купить рыбу? В мире свежая рыба – почти везде – продается не в магазинах, а с аукционов. Есть огромный рынок в Марселе, есть огромный рынок в Токио, в Нью-Йорке, и есть рынок на Гавайях. Просматривая ролик о рыбном аукционе на Гавайях, зададимся следующими вопросами: как устроен этот аукцион, почему как способ продажи выбран аукцион, а не магазин, почему правила продажи именно такие?

Итак, есть ряд, на котором лежит рыба, есть аукционист, который перечисляет цены. Он может перечислять их от большей к меньшей или наоборот, и он делает это быстро. При перечислении от большего к меньшему выясняется цена на одну конкретную рыбину. Если аукцион идет от меньшего к большему, аукционист повышает цену, пока есть по крайней мере два человека, готовые заплатить за рыбу, и делает это до тех пор, пока не останется один, который и купит ее за большую сумму. Все происходит очень быстро, и сами правила нацелены на то, чтобы быстро все продать.

Кажется, что продавать на аукционе значительно выгоднее, чем в магазине. На самом деле это не так, если товара много. Но если товар уникален или товара всего несколько штук, то аукционы работают замечательно – и особенно в ситуациях, когда вы точно не знаете, сколько человек готов заплатить. И в этом проявляется достоинство аукциона. Если товара у вас много, то получится рынок: есть огромное количество людей, которые хотят купить, есть большое количество людей, которые хотят продать, и вы, если хотите, можете накопить статистику и продавать как в магазине – и в магазине продажа будет гораздо быстрее.

Другой пример: как продают коров в США? Коров впускают в загон, начинается быстрый речитатив (таков язык аукционистов), продажа завершается, коров выгоняют и начинают заводить других. Прямое наблюдение: все происходит быстро – на продажу лота ушло около минуты. Здесь в одном месте продается много подобных «вещей»: один человек продает 36 коров, другой – целый табун, тогда как на рыбном аукционе продают по одной рыбине. Значит, не обязательно продавать по одной вещи, можно продавать группой.

Как продают цветы в Голландии? Вот пример знаменитого голландского аукциона. Цена здесь идет вниз. Есть пять маленьких комнат, в которых сидят люди и жмут на кнопки, с тем чтобы купить цветы. Через этот аукцион продается 21 миллион цветов, 80% из них идет на экспорт.

Как продают картины в Англии? Все происходит медленнее, аукционист делает движения руками, которые подсказывают, кто даст больше за данную картину. Явные правила таковы, что аукционист стоит и ждет: если кто-то каким-то образом подаст знак, он поднимает цену автоматом на 100 тысяч и считает, что этот человек готов купить и это текущая ставка. Закончится аукцион тогда, когда останется один человек, назвавший наибольшую цену, которую уже никто не сможет перебить. и аукционист скажет: «Продано».

Какие бывают аукционы? Из простых аукционов есть английский, с повышающейся ценой, и голландский, с понижающейся ценой (в тот момент, когда кто-то скажет «стоп», покупателю продается товар по цене, которая была, когда было сказано «стоп»). Есть аукционы другого типа – закрытые: брокер получает заявки, рассматривает их, по результатам заявок определяет победителя и цену. Если, ранжируя заявки, мы находим заявку с самой высокой ценой и продаем по ней, это будет аукцион 1-й цены. Аукцион 2-й цены используется реже, но очень интересен. Это аукцион, в котором мы получили заявки, выбрали самую высокую заявку и продаем тому, кто ее предложил, но цена продажи – вторая по величине заявка, то есть максимальная заявка от конкурента. Есть аукцион, где «платят все». Все люди делают ставки (фактически они кладут деньги на стол), организатор определяет, кто поставил больше всех, и этот человек становится победителем и забирает все деньги. Вы платите, но можете как выиграть, так и проиграть. Если игроки, которые участвуют, ограничены в средствах, то, как кажется, это самый лучший для продажи аукцион. Побеждает именно тот, который потратил больше всех. Как аукцион этого типа можно рассматривать (и исследовать) политическую игру – избирательную кампанию, где каждый участник тратит средства на предвыборную борьбу, в которой в итоге побеждает только один из кандидатов.

2. Голландский аукцион (и аукцион 1-й цены).
Стратегия: ставка. Есть ценность, и вам нужно определить ценность, при которой вы поднимете руку и скажете «стоп». Выигрывает участник с самой большой ценностью, и он будет платить эту ценность. Таким образом, голландский аукцион и аукцион 1-й цены стратегически эквивалентны как игры. Чем больше вы ставите, тем больше вероятность выигрыша, но тем меньше сам выигрыш, соответственно, нужно эти два куска балансировать.

Что же лучше: голландский или английский аукцион? Теорема Викри (за которую Уильям Викри получил Нобелевскую премию по экономике) гласит: они одинаковы.

Роджер Майерсон в 1981 году написал статью, которая отвечает на вопрос: «Как продать ваш дом с максимальной выгодой», и за это он тоже получил Нобелевскую премию (конечно, не за ответ, а за описание внутренней механики). Майерсон задал вопрос: «Как лучше продать товар?» Проблема в том, что способов продаж существует огромное количество. Мы уже увидели набор простых способов, но их можно комбинировать. Первое утверждение Роджера Майерсона – это принцип откровенности, который говорит о том, что, какая бы у вас сложная схема продажи ни была, для этой сложной схемы существует простая схема, прямой механизм, когда вы напрямую спрашиваете людей: «Какая ваша ценность?» Механизм заключается в том, что есть два правила: функция размещения товара и функция платежей. Согласно принципу откровенности, какой бы ни была игра, существует прямая игра, прямой механизм (где люди сообщают ценности), такая, что все говорят ценности правдиво, и результат этой игры ровно такой же, как в оригинальной.

Теорема об эквивалентности доходов говорит: в двух механизмах с одинаковой функцией размещения каждый участник каждого конкретного типа (в ожидании) будет платить одинаково, а значит, если мы сагрегируем все платежи, ожидаемый доход продавца будет одинаковый.

В английском аукционе выигрывает тот, у которого самая большая ценность. Это значит, что функция размещения товара в английском аукционе считает, какой из репортов самый большой, и отдает этому человеку весь товар. В голландском аукционе, если предположения у всех участников одинаковые, то чем больше ценность, тем больше будет ставка. Человек, который поставил больше всех, будет иметь самую высокую ценность. Если так, то функция размещения товара в голландском аукционе будет ровно такая же: у кого ценность больше всех, тот и победил.

Если мы возьмем аукцион, в котором платят все, там тоже функция размещения товара будет такая, что выигрывает тот, у кого самая большая ценность. Это значит, что все аукционы одинаковы с точки зрения доходов продавцов. Это еще не ответ на вопрос об оптимальном механизме. Оптимальный механизм в случае одинаковых представлений – это простой аукцион с правильно подобранной резервной ценой, минимальной ценой, по которой продавец готов продавать товар. И все аукционы – оптимальные механизмы: среди всех возможных способов продажи они все максимизируют доход продавца.

Теорему об эквивалентности доходов можно применить и другим способом. Если я знаю, что аукцион 1-й цены или голландский аукцион эквивалентны английскому аукциону (а в английском аукционе я знаю, сколько человек платит, если выигрывает: он платит ожидаемую вторую ставку), соответственно, я знаю, какая стратегия тогда в аукционе 1-й цены: я делаю ставку равной максимальной из ставок конкурентов (при условии, что все ставки конкурентов ниже моей).

Пример популярного аукциона – это eBay. Правила аукциона – за кадром: фактически это английский аукцион. Он не явный, не повышающейся цены, но вы делаете ставки. Самая большая цена (это текущий победитель), – то, что он платит, пока аукцион не закончился. Это статический и динамический аукцион: любой человек может сделать ставку в любой момент – если ставка самая высокая, возможным победителем станет новый человек.

Источник

Часть 1. Теория Аукционов

Тема 1. Аукционы с частными оценками стоимости:

Содержание: Цели проведения аукционов. Четыре стандартных аукциона. Примеры. Понятия эффективности и оптимальности аукционов. Модель с частными оценками стоимости. Вывод оптимальной стратегии в аукционах первой и второй цены с частными оценками. Подсчет ожидаемого дохода продавца.

Основные понятия и результаты:

Аукцион – механизм распределения объекта (товара, услуги) между покупателями, если его истинная стоимость не известна продавцу.

Четыре стандартных аукциона:

Английский аукцион: В английском аукционе продавец называет стартовую цену, участники делают ставки, последовательно повышая цену продажи объекта. Если нет больше желающих повысить текущую ставку, то участник, сделавший последнюю ставку, получает объект по цене последней ставки.

Голландский аукцион: В голландском аукционе торг начинается с очень высокой цены, которая постепенно снижается продавцом. Участник, желающий купить объект по текущей цене, сигнализирует об этом. Первый участник, подавший сигнал, получает объект по текущей цене.

Закрытый аукцион первой цены: Все участники аукциона подают свои ставки в запечатанных конвертах. Участник, предложивший максимальную ставку, получает объект и платит цену, равную своей ставке.

Закрытый аукцион второй цены (аукцион Викри): Все участники аукциона подают свои ставки в запечатанных конвертах. Участник, предложивший максимальную ставку, получает объект и платит цену, равную второй сверху ставке, т.е. ставке ближайшего конкурента.

Предположения о характере информации, которой обладают участники аукциона, и влиянии этой информации на ценность объекта для покупателей, определяют стратегии покупателей.

Пусть в аукционе участвуют N агентов ( ), v_i– оценка стоимости объекта i-м участником, t_i – сигнал i-го участника о стоимости объекта.

Покупатели обладают частными, независимыми оценками стоимости объекта, если оценка каждого участника не зависит от оценок других покупателей, а зависит только от информации об объекте самого участника. В этом случае оценки всех покупателей v_i – независимые случайные величины.

Покупатели обладают чистой общей оценкой стоимости объекта (purecommonvalues), если действительная оценка стоимости одинакова для всех (стоимость месторождения) и не зависит от того, кто из участников получил тот или иной сигнал:

Покупатели обладают общими оценками стоимости объекта (common values), если оценка стоимости объекта каждого покупателя зависит не только его информации, но и от информации других участников аукциона, при этом собственная информация и информация других участников по-разному влияют на оценку:

Аукцион называется оптимальным, если он максимизирует ожидаемый доход продавца.

Аукцион называется эффективным, если в результате аукциона объект всегда достается участнику с наибольшей оценкой объекта. В этом случае достигается максимум общественного благосостояния.

Рассмотрим случай частных независимых оценок. Пусть все оценки v_i – независимые, одинаково распределенные случайные величины на отрезке [0,δ], F(x) – функция распределения этих случайных величин, f(x) – плотность распределения. Обозначим через Y_i – максимальную оценку всех участников кроме i:

Утверждение. В модели с симметричными участниками с независимыми частными оценками равновесная стратегия i-го участника с оценкой v_i в закрытом аукционе первой цены определяется по формуле:

.

Утверждение. В модели с симметричными участниками с независимыми частными оценками слабо доминирующей стратегией i-го участника с оценкой v_i в закрытом аукционе второй цены является стратегия объявлять ставку, равную своей оценке:

Задачи для подготовки:

1.1. В модели частных оценок докажите, что стратегия делать ставку, равную оценке, является для участника слабо доминирующей, даже если совместное распределение оценок участников коррелировано.

1.2. Рассмотрите аукцион первой цены. В аукционе участвуют два покупателя с независимыми оценками θ_i, равномерно распределенными на отрезке [0,1]. Пусть резервная цена продавца равна 0.

a) Найдите оптимальные функции ставок участников, имеющие линейный вид: .

b) Найдите ожидаемый выигрыш продавца.

1.3. Рассмотрим аукцион между 2 участниками, имеющими частные независимые оценки распределенные в соответствии с функцией распределения F. На аукционе второй цены, где платят все, участники одновременно подают заявки в запечатанных конвертах. Выигрывает участник с наибольшей ставкой, и оба участника платят вторую по величине ставку.

1) Найдите единственную функцию ставок в симметричном равновесии.

2) Выше или ниже ставок в аукционе первой цены, где платят все, будут искомые ставки?

3) Найдите формулу для ожидаемого дохода продавца.

Литература по теме:

· Джейли, Рени, Микроэкономика, 2011, глава 9

· Klemperer, P, «Auctions: Theory and Practice”, Princeton University Press, (2004);

· V. Krishna, “Auction Theory”, 2010, Chapters 1,2.

Тема 2. Теорема об эквивалентности доходов

Содержание:Понятие эквивалентности аукционов. Эквивалентность английского аукциона и закрытого аукциона второй цены. Ожидаемый доход продавца в четырех стандартных аукционах. Теорема об эквивалентности доходов (ТЭД). Использование ТЭД для нахождения равновесных стратегий в аукционах.

Основные понятия и результаты:

Аукцион называется стандартным, если по правилам аукциона объект всегда переходит к участнику, сделавшему максимальную ставку.

Два аукциона эквивалентны, если в этих аукционах совпадают равновесные стратегии участников, цена продажи объекта, ожидаемые платежи покупателей и ожидаемый доход продавца.

Утверждение. В модели с частными независимыми оценками:

1. Голландский аукцион эквивалентен закрытому аукциону первой цены.

2. Английский аукцион эквивалентен закрытому аукциону второй цены.

Утверждение. В модели с независимыми частными оценками все четыре рассмотренных стандартных аукциона (голландский, английский, закрытые аукционы первой и второй цены) позволяют продавцу получить один и тот же ожидаемый доход:

.

Обозначим через — ожидаемый платеж игрока с оценкой x. Например, ожидаемый платеж игрока в закрытом аукционе первой цены равен

Теорема об эквивалентности дохода (ТЭД)

Пусть оценки участников: 1) частные, независимые; 2) одинаково распределенные; 3) все участники нейтральны к риску. Тогда в любом стандартном аукционе существует симметричное равновесие с возрастающими равновесными стратегиями участников, в котором ожидаемый платеж игрока с оценкой 0 равен нулю, позволяющее продавцу получить один и тот же ожидаемый доход.

Следствие. Пусть выполнены условия ТЭД, тогда независимо от формы аукциона ожидаемый платеж игрока с оценкой x равен

Задачи для подготовки:

2.1. Рассмотрим аукцион между N агентами с частными независимыми оценками, являющийся гибридом между закрытыми аукционами первой и второй цены. В этом аукционе побеждает участник, сделавший максимальную ставку, а его платеж равен выпуклой комбинации максимальной и второй сверху из сделанных ставок. Так, если побеждает i-ый участник, то он платит сумму . Воспользовавшись, и не воспользовавшись теоремой об эквивалентности доходов, найдите равновесную функцию ставок в симметричном равновесии, если оценки всех участников распределены в соответствии с функцией распределения F на отрезке [0,w].

2.2. Рассмотрим аукцион между N участниками, имеющими частные независимые оценки распределенные в соответствии с функцией распределения F. Аукцион устроен следующим образом: все участники одновременно подают заявки в запечатанных конвертах, участник с максимальной ставкой получает объект и ничего за это не платит, остальные участники выплачивают суммы, равные их ставкам.

1) Воспользуйтесь теоремой об эквивалентности доходов продавца для нахождения равновесной стратегии в симметричном равновесии для описанного выше аукциона.

2) Пусть оценки участников распределены в соответствии с , на промежутке [0,∞). Найдите функции ставок участников в симметричном равновесии для этого случая.

Литература по теме:

· Джейли, Рени, Микроэкономика, 2011, глава 9;

· V. Krishna, “Auction Theory”, 2010, Chapter 3;

· Riley, JG., WF Samuelson, “Optimal auctions”,— The American Economic Review, 1981.

Тема 3.Теорема об эквивалентности доходов: случаи нарушения условий теоремы (отсутствие нейтральности к риску, асимметрия между участниками)

Содержание: Аукционы первой и второй цены для участников-рискофобов (рискофилов): вывод равновесных стратегий в аукционах первой и второй цены. Сравнение ожидаемого дохода продавца в аукционах первой и второй цены. Асимметрия между участниками аукционов: условие на равновесные стратегии в аукционе первой цены, соотношение равновесных стратегий «слабых» и «сильных» участников в аукционе первой цены, неэффективность аукциона первой цены, поведение на аукционе второй цены.

Основные понятия и результаты

Рассмотрим аукцион между участниками рискофобами, т.е. участниками с вогнутыми функциями полезностями u(x): u(0)=0, u’(x)>0, u’’(x) закрытый аукцион первой цены и закрытый аукцион второй цены приносят разные ожидаемые доходы продавцу.

Утверждение. Пусть участники аукциона – рискофобы, чьи предпочтения описываются одной и той же функцией полезности 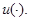В модели с частными, независимыми, симметричными оценками ожидаемый доход продавца в аукционе первой цены выше, чем в аукционе второй цены.

Объяснение. Для рискофоба потери в случае неполучения объекта при снижении ставки более болезненны, чем выигрыш от снижения платежа. Поэтому в аукционе первой цены ставка рискофоба будет выше, чем ставка агента нейтрального к риску с той же оценкой стоимости объекта:

Вследствие этого, ожидаемый доход продавца в аукционе первой цены выше, если покупатели-рискофобы, а не нейтральны к риску.

В аукционе второй цены равновесная стратегия участников-рискофобов такая же, как в случае участников нейтральных к риску: Поэтому ожидаемый доход продавца не меняется (по сравнению со случаем нейтральных к риску участников).

Пусть участники аукциона асимметричны, т.е. их оценки получены из разных распределений. Рассмотрим случай N=2, .

Утверждение. В закрытом аукционе второй цены стратегия является слабо доминирующей, несмотря на наличие асимметрии.

Для закрытого аукциона первой цены не существует симметричного равновесия и единой формулы для оптимальной стратегии.

Обозначим через — обратную функцию к функции ставок j-го игрока, — распределение ставок j-го игрока. Пусть — максимальная ставка обоих участников.

Утверждение. Стратегии β₁, β₂ являются равновесными в асимметричном аукционе первой цены, если выполняются следующие условия:

Опр (*). Оценки участника 1 стохастически выше оценок участника 2, если и для любого выполняется: В этом случае участник 1 называется «сильным», участник 2 – «слабым».

Утверждение. Пусть оценки участника 1 стохастически выше оценок участника 2 в смысле определения (*). Тогда в закрытом аукционе первой цены «слабый» участник 2 делает ставки более агрессивно, чем сильный участник 1, т.е.:

Задачи для подготовки:

3.1. В аукционе участвуют 2 агента с частными независимыми оценками, равномерно распределенными на отрезке [0,1]. Участники аукциона являются рискофобами: их предпочтения заданы функцией полезности

1) Найдите функции ставок участников в симметричном равновесии в закрытых аукционах первой и второй цены.

2) Сравните ожидаемые доходы продавца в каждом из аукционов.

3.2. В аукционе участвуют N агентов с частными независимыми оценками. Функция распределения – квадратичная на [0,1]: 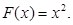Участники аукциона являются рискофилами: их предпочтения заданы функцией полезности Найдите функции ставок участников в симметричном равновесии в закрытых аукционах первой и второй цены. Сравните ожидаемые доходы продавца в каждом из аукционов.

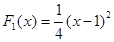
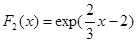
3.3.В аукционе участвуют 2 агента с частными независимыми оценками. Оценка первого участника распределена в соответствии с функцией распределения на отрезке [1,3], а оценка 2-го участника – в соответствии с функцией на отрезке [0,3].

1) Покажите, что стратегии являются равновесными в аукционе первой цены.

2) Сравните ожидаемые выигрыши продавца в аукционе первой и второй цены.

3) Верно ли, что аукцион первой (второй) цены является эффективным? Почему?

Литература по теме:

· Джейли, Рени, Микроэкономика, 2011, глава 9

· V. Krishna, “Auction Theory”, 2010, Chapter 4.

Тема 4. Дизайн механизмов и поиск оптимального механизма продажи

Содержание: Определение индивидуально рационального и совместимого по стимулам прямого механизма продажи. Определение и вывод оптимального механизма продажи объекта. Эффективность оптимального механизма. Реализация оптимального механизма через четыре стандартных аукциона с резервными ценами

Основные понятия и результаты

Механизм продажи определяется совокупностью (B, π, μ), где B – множество возможных сообщений, 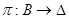— правило распределения объекта, — правило распределения выплат.

Механизм продажи прямой, если множество возможных сообщений B_i совпадает с множеством оценок X_i.

По принципу выявления можно ограничить рассмотрение прямыми механизмами, в которых каждый участник правдиво объявляет свою оценку. Поэтому далее будут рассматриваться прямые механизмы продажи (Q, M), где — правило распределение объекта, предписывающее с какой вероятностью каждый участник получает объект для , а — правило распределения выплат.

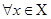
Пусть — вероятность i-го участника получить объект, объявляя оценку z_i, — ожидаемый платеж i-го участника при объявлении z_i, — ожидаемая полезность i-го участника с оценкой x_i, если он объявляет оценку z_i.

Прямой механизм (Q, M) совместим по стимулам, если для любого i и любого x_i функция достигает своего максимума по z_i в точке x_i, то есть при правдивом объявлении оценок.

Утверждение. Механизм прямой продажи (Q, M) совместим по стимулам тогда и только тогда, когда для любого участника i выполняются следующие два свойства:

1) не убывает по x_i.

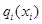
2)

Прямой механизм (Q, M) индивидуально рационален, если в правдивом равновесии любой участник, независимо от его оценки x_i, получает неотрицательный ожидаемый выигрыш:

Механизм прямой продажи оптимален, если он позволяет получить продавцу максимальный ожидаемый доход, и при этом совместим по стимулам и индивидуально рационален.

Утверждение. Пусть N участников механизма имеют независимые частные оценки, причем функции виртуальных оценок строго возрастают по x_i для любого i. Тогда механизм прямой продажи (Q, M), удовлетворяющий свойствам:

приносит продавцу максимальный ожидаемый доход, т.е. является оптимальным.

Утверждение. Пусть N участников механизма имеют независимые частные оценки, полученные из одного и того же распределения с функцией распределения F(x), причем функция виртуальных оценок строго возрастает по x. Тогда аукцион второй цены с резервной ценой является оптимальным механизмом.

Оптимальный механизм не обязательно является эффективным. Неэффективность может возникать по двум причинам:

1) Продавец удерживает объект, если , при этом оценки x_i могут быть положительны.

2) В случае асимметричных участников распределение объекта может быть не эффективно, т.к. основывается на сравнении виртуальных оценок , а не реальных оценок x_i.

Задачи для подготовки:

4.1. Пусть оценки участников независимы и равномерно распределены на отрезке [1,2]. Постройте аукцион, максимизирующий доход продавца.

4.2. В аукционе участвуют 2 агента с частными независимыми оценками. Оценка первого участника равномерно распределена на отрезке [0,1+k], оценка второго участника равномерно распределена на отрезке [0,1-k], где .

1) Найдите оптимальный механизм, т.е. правило распределение объекта и правило осуществления выплат, при которых ожидаемый доход продавца максимален. Найдите ожидаемый доход продавца в оптимальном механизме.

2) Пусть продавец решил продать объект, используя закрытый аукцион второй цены с резервной ценой r. Найдите значение r, при котором ожидаемый доход продавца максимален.

3) Сравните правило распределения объекта в аукционе второй цены с правилом распределения объекта в оптимальном механизме. Верно ли, что один из игроков имеет преимущество в аукционе второй цены? В оптимальном механизме? Почему?

4) Сравните ожидаемые доходы продавца в двух рассматриваемых механизмах. В каком случае они совпадают?

4.3. В аукционе участвуют 2 агента с частными независимыми оценками. Оценка первого участника равномерно распределена на отрезке [0,1], оценка второго участника распределена в соответствии с функцией распределения на [0,1].

1) Найдите оптимальный механизм, т.е. правило распределение объекта и правило осуществления выплат, при которых ожидаемый доход продавца максимален. Найдите ожидаемый доход продавца в оптимальном механизме.

2) Сравните правило распределения объекта в обычном аукционе второй цены с правилом распределения объекта в оптимальном механизме. Какой из двух механизмов является эффективным? Почему?

3) Пусть продавец решил продать объект, используя закрытый аукцион второй цены с резервной ценой r. Найдите значение r, при котором ожидаемый доход продавца максимален. Сравните ожидаемые доходы продавца в аукционе второй цены с резервной ценой и в оптимальном механизме.

Литература по теме:

· Джейли, Рени, Микроэкономика, 2011, глава 9;

· V. Krishna, “Auction Theory”, 2010, Chapter5;

· Roger B. Myerson (1981), «Optimal Auction Design», Mathematics of Operations Research, 6 (1);

· Jeremy Bulow and John Roberts (1989), «The Simple Economics of Optimal Auctions», Journal of Political Economy 97 (5);

Тема 5. Аукционы с общими оценками стоимости.

Содержание: Понятие общих оценок стоимости. «Проклятие победителя». Отсутствие эквивалентности между английским аукционом и закрытым аукционом второй цены в модели с общими оценками. Вывод равновесных стратегий в закрытых аукционах первой и второй цены. Равновесная стратегия в английском аукционе. Сравнение ожидаемого дохода продавца в четырех стандартных аукционах в модели с общими оценками.

Основные понятия и результаты

Пусть — сигнал о стоимости объекта, имеющийся у участника i.

В модели с общими оценками стоимости оценка объекта i-ым участником зависит не только от его сигнала Х_i, но и от сигналов других участников:

1) сигнал каждого участника – несмещенная оценка стоимости объекта: ;

2) .

Проклятие победителя в модели с общими оценками возникает из-за того, что оценка объекта участником после того, как он узнал о своей победе в аукционе, ниже оценки, которая у него была изначально:

.

Тот факт, что участник победил, говорит о том, что этот участник переоценивал стоимость объекта по сравнению с другими покупателями. Чтобы скорректировать эффект проклятия победителя, участники аукционов с общими оценками должны понизить свои ставки.

В симметричной модели, которая будет рассматриваться далее, предполагается:

1. Все сигналы X_i получены из одного и того же распределения с функцией распределения F(x).

2. Оценки объекта каждым участником – симметричные функции собственного сигнала участника и сигналов других покупателей: для . При этом функция симметрична по последним N-1 аргументам.

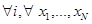
Обозначим . Это ожидаемая оценка первого участника в том случае, если его сигнал равен x, а максимальный сигнал других участников — y.

Утверждение. В закрытом аукционе второй цены в симметричном равновесии участники играют стратегию

т.е. ставка равна оценке стоимости для случая, когда максимальный сигнал других участников равен собственному сигналу агента.

В модели с общими оценками английский аукцион не эквивалентен закрытому аукциону второй цены, так как выявленная в ходе английского аукциона информация влияет на стратегии игроков.

Стратегия в английском аукционе имеет вид: 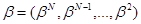, где — цена, при которой участник с сигналом x выходит из игры, если в аукционе участвуют k игроков, а другие N-k игроков вышли при ценах .

Утверждение. Следующие стратегии являются равновесными в английском аукционе:

,

где x_k – значение сигнала, при котором участник выходит из аукциона с k участниками при цене p_k: .

Утверждение. В закрытом аукционе первой цены в симметричном равновесии участники играют стратегию , определяемую из уравнения:

где G(x|x)— функция распределения при условии X₁=x.

Утверждение. Если сигналы участников независимы, то продавец получает один и тот же ожидаемый доход в закрытых аукционах первой и второй цены.

Утверждение. Если сигналы участников аффилиированы (коррелированны), то ожидаемый доход продавца в английском аукционе превышает доход в закрытом аукционе второй цены, что в свою очередь больше ожидаемого дохода в аукционе первой цены.

Задачи для подготовки:

5.1. Рассмотрим аукцион между N участниками, имеющими общие оценки стоимости объекта. Пусть сигналы всех участников x_i – независимые случайные величины, равномерно распределенные на отрезке [0, 1]. Оценка стоимости объекта для каждого участника представима в виде функции:

1) Найдите равновесную стратегию участников в закрытом аукционе второй цены . Верно ли, что ставка каждого участника ниже его сигнала? Найдите ожидаемый платеж каждого участника при условии его выигрыша и ожидаемый доход продавца.

2) Найдите равновесную стратегию участников в закрытом аукционе первой цены . Сравните найденную оптимальную ставку с ожидаемым платежом участника в закрытом аукционе второй цены. Какой вывод можно сделать о размере ожидаемого дохода продавца в аукционе первой цены?

3) Найдите равновесную стратегию участников в английском аукционе. При какой цене в игре остается только один участник? Чему равен ожидаемый доход продавца в английском аукционе?

4) Верно ли утверждение теоремы об эквивалентности доходов в этой модели? Почему? В каких случаях в модели с общими оценками не выполняется теорема об эквивалентности доходов?

.

Пусть перед аукционом участники получили сигналы: . Какие ставки будут делать участники в закрытом аукционе второй цены? В английском аукционе? По какой цене будет продан объект в каждом из случаев?

Литература по теме:

· Milgrom, P. and R., Weber, «A Theory of Auctions and Competitive Bidding», Econometrica 50 (5), (1982);

· Milgrom, P. and R., Weber, «The Value of Information in a Sealed-Bid Auction», Journal of Mathematical Economics, 10 (1), (1982);

Вопросы и задачи для подготовки к экзамену по теме «Теория аукционов»:

Задача 1.

Рассмотрим аукцион между N участниками, имеющими частные независимые оценки объекта, равномерно распределенные на [0,1].

2) Пусть агенты – рискофилы, чьи предпочтения описываются функцией полезности Как изменится для рискофилов равновесная функция ставок в аукционе первой цены? В аукционе второй цены? Вычислите равновесные стратегии. Какой из двух аукционов предпочтительнее для продавца? (без вычислений ожидаемого дохода)

3) Пусть как в п. 1) агенты нейтральны к риску, а N=2. Рассмотрим следующую модификацию аукциона второй цены. Участники подают ставки в запечатанных конвертах. Игрок, сделавший максимальную ставку, получает объект. Цена объекта равна второй по величине ставке. После установления победителя организатор аукциона подбрасывает монетку. Если выпадает «орел», то указанную выше сумму выплачивает победитель, если «решка», то платит проигравший.

Воспользовавшись теоремой об эквивалентности дохода, найдите равновесную стратегию в симметричном равновесии для этого аукциона.

Задача 2.

Рассмотрим аукцион с двумя потенциальными покупателями, имеющими частные независимые оценки. Функция распределения оценок обоих участников – квадратичная на [0,1]:

1) Найдите оптимальный аукцион, т.е. аукцион, максимизирующий ожидаемый доход продавца.

2) Подсчитайте, с какой вероятностью в этом оптимальном аукционе объект остается у продавца. Изобразите графически, при каких значениях оценок объект переходит к первому или второму участнику.

3) Найдите ожидаемый платеж каждого покупателя 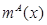и ожидаемый доход продавца в оптимальном аукционе.

4) Пусть функция распределения оценки первого участника квадратичная, а оценка второго участника распределена равномерно на [0,1]. Найдите оптимальный механизм (т.е. правило распределение объекта и правило выплат для этого случая. Изобразите графически. Каким образом можно реализовать данный оптимальный механизм?

Задача 3.

1) Найдите равновесную функцию ставок в аукционе первой цены.

2) Воспользовавшись теоремой об эквивалентности дохода, найдите ожидаемый платеж игрока с оценкой x. Найдите ожидаемый доход продавца. Верно ли, что ожидаемый доход продавца в английском аукционе будет таким же?

3) Найдите оптимальную резервную цену в аукционе второй цены.

4) Найдите оптимальный прямой механизм продажи. Сравните с результатами предыдущего пункта.

Задание 4.

Рассмотрим аукцион между N участниками, имеющими частные независимые оценки объекта, равномерно распределенные на [0,1].Сравним поведение игроков в модели с частными оценками с поведением в модели с общими оценками стоимости. Пусть сигналы всех участников x_i – независимые случайные величины, равномерно распределенные на отрезке [0, 1]. Оценка стоимости объекта для каждого участника равна среднему арифметическому сигналов всех участников: Найдите равновесную стратегию участников в закрытом аукционе второй цены . При каких значениях N равновесная ставка игрока в модели с общими оценками совпадает с равновесной ставкой в аукционе с частными оценками? При каких N ставка в модели с общими оценками ниже? Дайте простое интуитивное объяснение этому факту (нужно вспомнить особенности модели с общими оценками стоимости).

Вопросы для повторения:

1) Какой из двух стандартных аукционов – закрытый аукцион первой цены или закрытый аукцион второй цены – лучше использовать с точки зрения продавца? С точки зрения общественных интересов? Как это связано с понятиями эффективности и оптимальности?

2) Верно ли, что если участники аукциона асимметричны, то оптимальный механизм всегда не эффективен? Объясните.

3) Если участники аукциона – рискофобы, условия теоремы об эквивалентности дохода не выполняются. Какой из четырех стандартных аукционов позволяет продавцу получить наибольший ожидаемый доход в этом случае? Дайте интуитивное объяснение с точки зрения выбора оптимальной стратегии участника-рискофоба.

4) Рассмотрим аукцион между двумя асимметричными участниками: оценки объекта «сильного» участника стохастически выше оценок «слабого участника». Объясните интуитивно, почему в равновесии «слабый» участник делает ставки более агрессивно, чем «сильный».

5) Верно ли, что поведение участников аукциона в модели с общими оценками принципиальным образом отличается от поведения в случае частных оценок? В чем состоят различия и сходства? Объясните.

6) С какими трудностями сталкиваются организаторы аукционов на практике? Опишите преимущества и недостатки английского аукциона и закрытых аукционов первой (второй) цены.

Источник