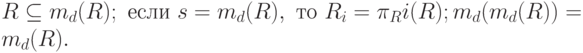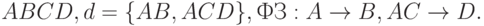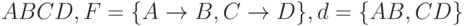в каком случае проекции отношения являются декомпозицией без потерь
Декомпозиция отношения без потерь. Теорема Хеза
Как было показано выше, алгоритм нормализации состоит в выявлении функциональных зависимостей предметной области и соответствующей декомпозиции отношений. Предположим, что мы уже имеем работающую систему, в которой накоплены данные. Пусть данные корректны в текущий момент, т.е. факты предметной области правильно отражаются текущим состоянием базы данных. Если в предметной области обнаружена новая функциональная зависимость (либо она была пропущена на этапе моделирования предметной области, либо просто изменилась предметная область), то возникает необходимость заново нормализовать данные. При этом некоторые отношения придется декомпозировать в соответствии с алгоритмом нормализации. Возникают естественные вопросы – что произойдет с уже накопленными данными? Не будут ли данные потеряны в ходе декомпозиции? Можно ли вернуться обратно к исходным отношениям, если будет принято решение отказаться от декомпозиции, восстановятся ли при этом данные?
Для ответов на эти вопросы нужно ответить на вопрос – что же представляет собой декомпозиция отношений с точки зрения операций реляционной алгебры? При декомпозиции мы из одного отношения получаем два или более отношений, каждое из которых содержит часть атрибутов исходного отношения. В полученных новых отношениях необходимо удалить дубликаты строк, если таковые возникли. Это в точности означает, что декомпозиция отношения есть не что иное, как взятие одной или нескольких проекций исходного отношения так, чтобы эти проекции в совокупности содержали (возможно, с повторениями) все атрибуты исходного отношения. Т.е., при декомпозиции не должны теряться атрибуты отношений. Но при декомпозиции также не должны потеряться и сами данные. Данные можно считать не потерянными в том случае, если возможна обратная операция – по декомпозированным отношениям можно восстановить исходное отношение в точности в прежнем виде. Операцией, обратной операции проекции, является операция соединения отношений. Имеется большое количество видов операции соединения. Т.к. при восстановлении исходного отношения путем соединения проекций не должны появиться новые атрибуты, то необходимо использовать естественное соединение.
Определение. Проекция отношения на множество атрибутов называется собственной, если множество атрибутов является собственным подмножеством множества атрибутов отношения (т.е. множество атрибутов не совпадает с множеством всех атрибутов отношения ).
Определение. Собственные проекции и отношения называются декомпозицией без потерь, если отношение точно восстанавливается из них при помощи естественного соединения для любого состояния отношения :
Рассмотрим пример, показывающий, что декомпозиция без потерь происходит не всегда.
Пример. Пусть дано отношение :
Таблица 7 Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров |
Рассмотрим первый вариант декомпозиции отношения на два отношения:
Таблица 8 – Отношение
Таблица 9 – Отношение
| ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | |
| Петров |
Естественное соединение этих проекций, имеющих общий атрибут «ЗАРПЛАТА», очевидно, будет следующим (каждая строка одной проекции соединится с каждой строкой другой проекции):
Таблица 10 – Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Иванов | ||
| Петров |
Итак, данная декомпозиция не является декомпозицией без потерь, т.к. исходное отношение не восстанавливается в точном виде по проекциям.
Рассмотрим другой вариант декомпозиции:
Таблица 11– Отношение
| НОМЕР | ФАМИЛИЯ |
| Иванов | |
| Петров |
Таблица 12 – Отношение
Таблица 13 – Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Сидоров |
Кажется, что этого не может быть, т.к. значения в атрибуте «НОМЕР» повторяются. Но мы же ничего не говорили о ключе этого отношения! Сейчас проекции будут иметь вид:
Таблица 14 – Отношение
| НОМЕР | ФАМИЛИЯ |
| Иванов | |
| Петров | |
| Сидоров |
Таблица 15 – Отношение
Естественное соединение этих проекций будет содержать лишние кортежи:
Таблица 16 Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Петров | ||
| Сидоров | ||
| Сидоров |
Вывод. Таким образом, без дополнительных ограничений на отношение нельзя говорить о декомпозиции без потерь.
Такими дополнительными ограничениями и являются функциональные зависимости. Имеет место следующая теорема Хеза:
Т.к. алгоритм нормализации (приведения отношений к 3НФ) основан на имеющихся в отношениях функциональных зависимостях, то теорема Хеза показывает, что алгоритм нормализации является корректным, т.е. в ходе нормализации не происходит потери информации.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
16. Декомпозиция без потерь
Декомпозиция без потерь. Это значит, что после разбиения ненормализованной таблицы на несколько более мелких ее можно при желании объединить обратно без потери данных. Такое объединение обычно производится, конечно, не на уровне самой базы данных, а на уровне запросов.
Считаются правильными такие декомпозиции отношения, которые обратимы, т. е. имеется возможность собрать исходное отношение из декомпозированных отношений без потери информации. Такие декомпозиции называются декомпозициями без потерь.
екомпозиция отношений проводится, чтобы исключить избыточное дублирование в отношениях. Выделяют два типа декомпозиций отношений: без потерь и с потерями. Декомпозиция без потерь происходит тогда, когда после соединения вновь полученных отношений получается исходное отношение. В ряде случаев невозможно провести декомпозицию без потерь, т.к. простое выделение ФЗ в отдельное отношение не дает желаемого результата. В этом случае надо решить:
· или поддерживать избыточное дублирование;
· или теряем ФЗ и поддерживаем ее программным путем.
Выбор должен быть обоснован.
Существуют следующие виды декомпозиций:
1. Декомпозиция на минимальном покрытии (если в отношении только один ключ);
2. Декомпозиция на кольцевом покрытии (если в отношении несколько ключей и существуют эквивалентные левые части функциональных зависимостей);
3. Декомпозиция по теореме Хеза (если ни один из вышеперечисленных методов неприемлем или не дает желаемого результата).
Смысл декомпозиции заключается в том, что исходное отношение разбивается на несколько отношений таким образом, чтобы в последствии соединение вновь образованных отношений позволило получить исходное отношение. Такая декомпозиция получила название декомпозиции без потерь.
Процесс декомпозиции следует всегда начинать со следующих операций:
· с определения (идентификации) всех атрибутов, подлежащих хранению в БД.
· установления между ними функциональных зависимостей.
Процесс декомпозиции осуществляется поэтапно, при этом на каждом этапе (в большинстве случаев) исходное отношение разбивается только на два отношения, затем делается вывод о необходимости продолжения декомпозиции, и если она необходима, то процесс продолжается.
Декомпозиция не всегда является обязательной, и в ряде случаев проектировщик должен принимать решение, выбирая между избыточностью и независимостью отношений.
Декомпозиция снимает большинство проблем, связанных с выполнением операций – удаление, добавление и редактирование, за счет исключения избыточного дублирования информации.
Методы проектирования логических моделей реляционных баз данных. Декомпозиция и синтез отношений
Декомпозиция схем отношений, свойства соединения без потерь и сохранения ФЗ
Одной из целей проектирования реляционной базы данных является построение декомпозиции (разбиения) универсального отношения на совокупность отношений, удовлетворяющих требованиям нормальных форм.
Пример. Декомпозиция с потерей информации
Пусть 
Эти свойства следуют из определения естественного соединения. Первое свойство используется при проверке, обладает ли декомпозиция свойством соединения без потерь относительно некоторого множества ФЗ.
Рассмотрим алгоритм проверки свойства соединения без потерь.
Алгоритм. Проверка декомпозиции на свойство соединения без потерь
Приведенный алгоритм позволяет корректно определить, обладает ли декомпозиция свойством соединения без потерь.
Схема отношения
Вывод. Декомпозиция d обладает свойством соединения без потерь.
Введем следующее определение.
Рассмотрим пример нарушения ФЗ при декомпозиции.
Пример. Нарушение ФЗ при декомпозиции
С другой стороны, декомпозиция может обладать свойством сохранения ФЗ, но не обладать свойством соединения без потерь. Например,
Таким образом, с точки зрения теории реляционных баз данных хорошая схема отношений реляционной базы данных должна по возможности отвечать следующим требованиям:
5rik.ru
Материалы для учебы и работы
Декомпозиция отношения без потерь. Теорема Хеза.
Как было показано выше, алгоритм нормализации состоит в выявлении функциональных зависимостей предметной области и соответствующей декомпозиции отношений. Предположим, что мы уже имеем работающую систему, в которой накоплены данные. Пусть данные корректны в текущий момент, т.е. факты предметной области правильно отражаются текущим состоянием базы данных. Если в предметной области обнаружена новая функциональная зависимость (либо она была пропущена на этапе моделирования предметной области, либо просто изменилась предметная область), то возникает необходимость заново нормализовать данные. При этом некоторые отношения придется декомпозировать в соответствии с алгоритмом нормализации. Возникают естественные вопросы – что произойдет с уже накопленными данными? Не будут ли данные потеряны в ходе декомпозиции? Можно ли вернуться обратно к исходным отношениям, если будет принято решение отказаться от декомпозиции, восстановятся ли при этом данные?
Для ответов на эти вопросы нужно ответить на вопрос – что же представляет собой декомпозиция отношений с точки зрения операций реляционной алгебры? При декомпозиции мы из одного отношения получаем два или более отношений, каждое из которых содержит часть атрибутов исходного отношения. В полученных новых отношениях необходимо удалить дубликаты строк, если таковые возникли. Это в точности означает, что декомпозиция отношения есть не что иное, как взятие одной или нескольких проекций исходного отношения так, чтобы эти проекции в совокупности содержали (возможно, с повторениями) все атрибуты исходного отношения. Т.е., при декомпозиции не должны теряться атрибуты отношений. Но при декомпозиции также не должны потеряться и сами данные. Данные можно считать не потерянными в том случае, если возможна обратная операция – по декомпозированным отношениям можно восстановить исходное отношение в точности в прежнем виде. Операцией, обратной операции проекции, является операция соединения отношений. Имеется большое количество видов операции соединения. Т.к. при восстановлении исходного отношения путем соединения проекций не должны появиться новые атрибуты, то необходимо использовать естественное соединение.
Определение. Проекция отношения на множество атрибутов называется собственной, если множество атрибутов является собственным подмножеством множества атрибутов отношения (т.е. множество атрибутов не совпадает с множеством всех атрибутов отношения ).
Определение. Собственные проекции и отношения называются декомпозицией без потерь, если отношение точно восстанавливается из них при помощи естественного соединения для любого состояния отношения :
Рассмотрим пример, показывающий, что декомпозиция без потерь происходит не всегда.
Пример. Пусть дано отношение :
Таблица 7 Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров |
Рассмотрим первый вариант декомпозиции отношения на два отношения:
Таблица 8 – Отношение
Таблица 9 – Отношение
| ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | |
| Петров |
Естественное соединение этих проекций, имеющих общий атрибут «ЗАРПЛАТА», очевидно, будет следующим (каждая строка одной проекции соединится с каждой строкой другой проекции):
Таблица 10 – Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Иванов | ||
| Петров |
Итак, данная декомпозиция не является декомпозицией без потерь, т.к. исходное отношение не восстанавливается в точном виде по проекциям.
Рассмотрим другой вариант декомпозиции:
Таблица 11– Отношение
| НОМЕР | ФАМИЛИЯ |
| Иванов | |
| Петров |
Таблица 12 – Отношение
Таблица 13 – Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Сидоров |
Кажется, что этого не может быть, т.к. значения в атрибуте «НОМЕР» повторяются. Но мы же ничего не говорили о ключе этого отношения! Сейчас проекции будут иметь вид:
Таблица 14 – Отношение
| НОМЕР | ФАМИЛИЯ |
| Иванов | |
| Петров | |
| Сидоров |
Таблица 15 – Отношение
Естественное соединение этих проекций будет содержать лишние кортежи:
Таблица 16 Отношение
| НОМЕР | ФАМИЛИЯ | ЗАРПЛАТА |
| Иванов | ||
| Петров | ||
| Петров | ||
| Сидоров | ||
| Сидоров |
Вывод. Таким образом, без дополнительных ограничений на отношение нельзя говорить о декомпозиции без потерь.
Такими дополнительными ограничениями и являются функциональные зависимости. Имеет место следующая теорема Хеза:
Т.к. алгоритм нормализации (приведения отношений к 3НФ) основан на имеющихся в отношениях функциональных зависимостях, то теорема Хеза показывает, что алгоритм нормализации является корректным, т.е. в ходе нормализации не происходит потери информации.
Базы данных. Вводный курс
9.3. Зависимости проекции/соединения и пятая нормальная форма
Приведение отношения к 4NF предполагает его декомпозицию без потерь на две проекции (как и в случае 2NF, 3NF и BCNF). Однако бывают (хотя и нечасто) случаи, когда декомпозиция без потерь на две проекции невозможна, но можно произвести декомпозицию без потерь на большее число проекций. Будем называть n-декомпозируемым отношением отношение, которое может быть декомпозировано без потерь на n проекций. До сих пор мы имели дело с 2-декомпозируемыми отношениями.
9.3.1. N-декомпозируемые отношения
Начнем с еще одного определения.
Тривиальная MVD всегда удовлетворяется. При A
9.3.2. Зависимость проекции/соединения
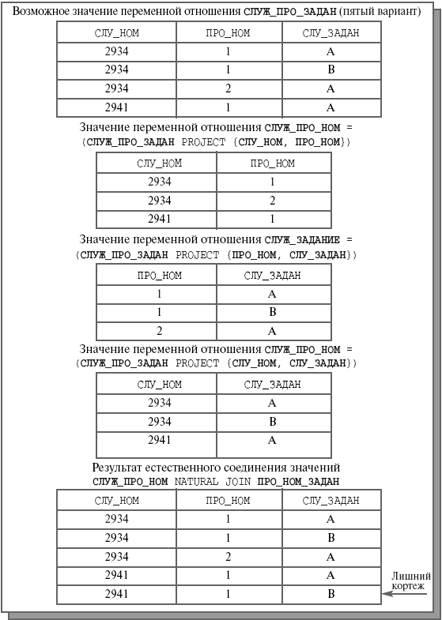
Это обычное ограничение реального мира, которое для отношения СЛУЖ_ПРО_ЗАДАН может быть сформулировано на естественном языке следующим образом:
Если служащий с номером сн участвует в проекте пн, и в проекте пн выполняется задание сз, и служащий с номером сн выполняет задание сз, то служащий с номером сн выполняет задание сз в проекте пн.
В общем виде такое ограничение называется зависимостью проекции/соединения. Вот формальное определение.
Рис. 9.3. Возможное значение переменной отношения СЛУЖ_ПРО_ЗАДАН (пятый вариант), результаты проекций и результат частичного естественного соединения
9.3.3. Аномалии, вызываемые наличием зависимости проекции/соединения
9.3.4. Устранение аномалий обновления в 3-декомпозиции
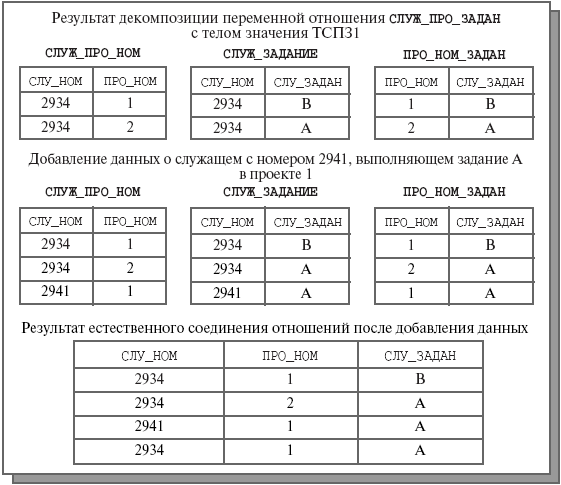
После выполнения декомпозиции трудности с обновлением автоматически снимаются. Действительно, декомпозируем отношение СЛУЖ_ПРО_ЗАДАН на три отношения: СЛУЖ_ПРО_НОМ <СЛУ_НОМ, ПРО_НОМ>, СЛУЖ_ЗАДАНИЕ <СЛУ_НОМ, СЛУ_ЗАДАН>и ПРО_НОМ_ЗАДАН <ПРО_НОМ, СЛУ_ЗАДАН>. Результат декомпозиции значения переменной отношения СЛУЖ_ПРО_ЗАДАН с телом BСПЗ1 показан в верхней части рис. 9.5.
Аналогично можно проиллюстрировать простоту и корректность операций удаления кортежей.
9.3.5. Пятая нормальная форма
Рис. 9.5. Иллюстрация декомпозиции отношения с зависимостью соединения
Легко убедиться, что нетривиальные PJD, подразумеваемые возможными ключами, существуют во всех отношениях с арностью, большей двух, первичный ключ которых не совпадает с заголовком отношения. Например, если в отношении СЛУЖ_ПРО_ЗАДАН атрибут СЛУ_НОМ является первичным ключом, то, очевидно, имеется PJD *(<СЛУ_НОМ, ПРО_НОМ>, <СЛУ_НОМ, СЛУ_ЗАДАН>) (это следует из теоремы Хита). Но такие зависимости проекции/соединения неинтересны с точки зрения проектирования базы данных, поскольку не порождают аномалии обновления. Поэтому общепринятое определение пятой нормальной формы выглядит следующим образом.
Таким образом, чтобы распознать, что данная переменная отношения R находится в 5NF, необходимо знать все возможные ключи R и все PJD этой переменной отношения. Обнаружение всех зависимостей соединения является нетривиальной задачей, и для ее решения нет общих методов. Поэтому на практике проектирование реляционных баз методом нормализации обычно завершается после достижения 4NF, и отношения, находящиеся в 4NF, как правило, находятся и в 5NF. Зачем же тогда была введена эта туманная и труднодостижимая пятая нормальная форма?
Ответ на этот естественный вопрос состоит в том, что 5NF является «окончательной» нормальной формой, которой можно достичь в процессе нормализации на основе проекций. «Окончательность» понимается в том смысле, что у отношения, находящегося в 5NF, отсутствуют аномалии обновлений, которые можно было бы устранить путем его декомпозиции. Другими словами, такие отношения далее нормализовать бессмысленно.
9.4. Заключение
Рассмотрим, насколько эти цели актуальны в современных условиях, когда объемы доступных носителей внешней памяти непрерывно возрастают, стоимость их падает, а современные серверы реляционных баз данных способны автоматически поддерживать целостность баз данных. Здесь следует отметить два важных обстоятельства.
Во-первых, теория реляционных баз данных и методы их проектирования активно развивались уже более 25 лет тому назад. Ситуация в области технологии аппаратуры и программного обеспечения тогда была совсем иной, чем сегодня, и хорошо нормализованные реляционные базы данных в значительной степени способствовали росту эффективности приложений.
Во-вторых, в то время реляционные базы преимущественно использовались в информационных системах оперативной обработки транзакций (On-Line Transaction Processing – OLTP). Характерные примеры таких систем мы отмечали в лекции 1 – банковские системы, системы резервирования билетов и мест в гостиницах. Системам категории OLTP свойственны частые обновления базы данных, поэтому аномалии обновлений, даже если их корректировка производится СУБД автоматически, могут заметно снижать эффективность приложения.
Сегодня на переднем крае приложений баз данных находятся системы категории оперативной аналитической обработки (On-Line Analytical Processing – OLAP). В подобных системах, в частности, системах поддержки принятия решений, базы данных в основном используются для выборки данных, поэтому аномалиями обновлений можно пренебречь, а объем этих баз настолько огромен, что можно пренебречь и избыточностью хранения.
Значит ли это, что подход к проектированию реляционных баз данных методом нормализации утратил свою роль? Нет!
Мир приложений баз данных в настоящее время огромен. Сегодня любое мало-мальски приличное предприятие использует хотя бы одно приложение баз данных – бухгалтерские, складские, кадровые системы. Это системы категории OLTP с частым обновлением данных и умеренными запросами к базе данных, не вызывающими соединений многих отношений. Для небольших компаний равно важны как эффективность информационных систем, так и стоимость используемых аппаратно-программных средств. Правильно спроектированные, хорошо нормализованные реляционные базы данных помогают решению корпоративных проблем.
Да, любое правильно развивающееся предприятие рано или поздно приходит к использованию систем категории OLAP, например, некоторой разновидности систем поддержки принятия решений (Decision Support System – DSS). В базах данных таких систем обновления очень редки, а запросы могут иметь произвольную сложность, включая соединения многих отношений. Но, во-первых, технологически правильно для системы OLAP поддерживать отдельную базу данных (обычно подобные базы данных называют хранилищами данных – DataWarehouse), а во-вторых, основными источниками данных для построения таких хранилищ данных являются базы данных систем OLTP. Так что актуальность правильно спроектированных баз данных OLTP-систем не уменьшается, а постоянно возрастает.
Следует ли из этого, что принципы нормализации непригодны для проектирования баз данных OLAP-приложений? И снова в ответ категорическое НЕТ! Возможно, окончательная схема такой базы данных должна быть денормализована из соображений повышения эффективности выполнения запросов. Но чтобы получить правильную денормализованную схему, нужно сначала понять, как выглядит нормализованная схема.
Основной вывод этой и предыдущей лекций можно сформулировать следующим образом. Пока мы остаемся в мире реляционных баз данных, для правильного проектирования базы данных необходимо понимать принципы нормализации, воспринимая их не как догму, а как руководство к действию. Кстати, это относится не только к «ручному» проектированию реляционных баз данных, но и к их проектированию с применением семантических моделей данных и CASE-средств, которые мы обсудим в следующих двух лекциях.