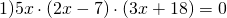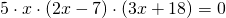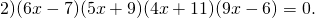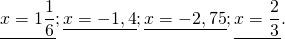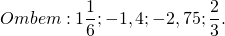в каком случае произведение равно нулю
Произведение равно нулю
В каком случае произведение равно нулю?
С помощью этого правила решают уравнения, в которых произведение нескольких множителей равно нулю. Уравнения вида «Произведение равно нулю» — одни из самых распространенных в математике. Их начинают изучать с 6 класса. В 6 классе множители представляют собой линейные уравнения.
Это уравнение вида «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю, поэтому приравниваем к нулю каждый из множителей:
5x=0 или 2x-7=0 или 3x+18=0.
Теперь решаем каждое из уравнений. Первое — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:
Второе и третье — линейные уравнения. Алгоритм решения: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Замечания.
1) Это уравнение также можно рассмотреть как произведение четырех множителей:
Рассуждаем так: поскольку произведение равно нулю, если хотя бы один из множителей равен нулю, а первый множитель 5≠0, приравниваем к нулю остальные множители:
x=0 или 2x-7=0 или 3x+18=0.
2) Поскольку перед буквой и перед скобками знак умножения можно не писать, условие уравнений обычно выглядят так:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
6x-7=o или 5x+9=0 или 4x+11=0 или 9x-6=0
6x=7 I:6 5x=-9 I:5 4x=-11 I:4 9x=6 I:9
В первом уравнении получили неправильную дробь. Выделяем из нее целую часть. Во втором и третьем уравнении ответ записываем в виде десятичной дроби. Для этого делим числитель на знаменатель уголком. В четвертом уравнении нужно сократить дробь в ответе
А как узнать, записать ответ в виде обыкновенной или в виде десятичной дроби? Любую ли обыкновенную дробь можно перевести в десятичную? Любую ли десятичную дробь можно перевести в обыкновенную? Об этом мы поговорим в следующий раз.
2 Comments
определение наверху неверное, т.к. произведение двух или более множителей равно нулю тогда и только тогда когда хотя-бы один из них равен нулю, а остальные не теряют смысла.
Мне понравился ход мысли Вашего учителя математики. Она расширила определение, чтобы ученики не забывали проверить, входят ли найденные корни в область допустимых значений уравнения (или неравенства).