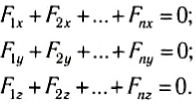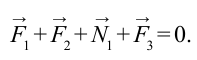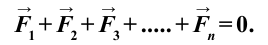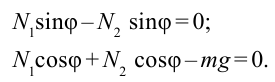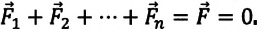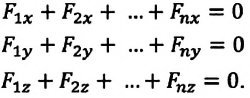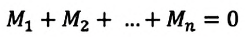в каком случае тело находится в равновесии

Условия равновесия тел

Равновесие тела

Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.

Условие равновесия тел

Чтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.

Равновесие вращающегося тела. Правило моментов

Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.

Определение. Правило моментов

Если алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.

В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.

Безразличное, устойчивое и неустойчивое равновесие

В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.

Линия, проведенная из центра масс башни пересекает основание приблизительно в 2,3 м от его центра.

Источник

В каком случае тело находится в равновесии

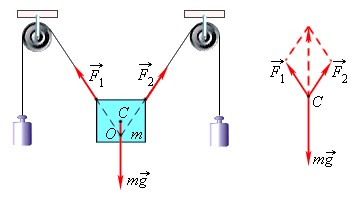
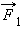
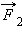
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс ), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.

Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.

Правило моментов : тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю :

В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов сил.

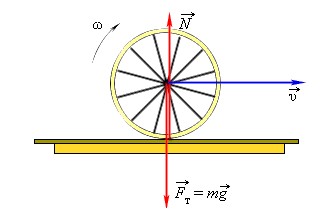
Катящееся по горизонтальной поверхности колесо – пример безразличного равновесия (рис. 1.14.3). Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Наряду с безразличным равновесием в механике различают состояния устойчивого и неустойчивого равновесия.

Состояние равновесия называется устойчивым, если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние.

При малом отклонении тела из состояния неустойчивого равновесия возникают силы или моменты сил, стремящиеся удалить тело от положения равновесия.

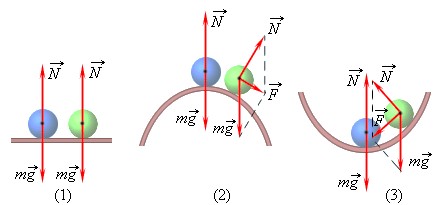
Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия. Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия (рис. 1.14.4).

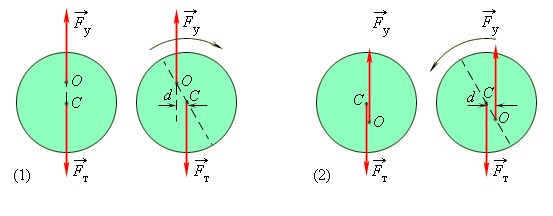
Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым. Если же центр масс расположен выше оси – состояние равновесия неустойчиво (рис. 1.14.5).

Источник

Содержание:

Условия равновесия тел:

Основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько сил, не движется с ускорением, а покоится или движется равномерно и прямолинейно. В последнем случае мы всегда можем выбрать другую инерциальную систему отсчета, в которой тело покоится, поэтому в дальнейшем будем изучать условия равновесия покоящихся тел.

Раздел механики, в котором изучаются условия равновесия тел, называется статикой.

Все опытные факты, которые мы рассмотрели в предыдущих параграфах, убеждают нас в том, что тело покоится, если равнодействующая всех сил, действующих на него, равна нулю.

Итак, первое условие равновесия тела: векторная сумма всех сил, приложенных к телу, равна нулю.
Если на тело действует n сил

Из этого условия следует, что и сумма проекций всех сил на любое направление тоже должна быть равна нулю. В частности, сумма проекций сил на оси выбранной декартовой системы координат равна нулю:

Фактически эти три равенства эквивалентны одному векторному равенству ( 1 ). Но с их помощью достаточно просто решать задачи, поскольку проекции сил — скалярные величины.

В повседневной жизни и технике часто встречаются тела, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, качели, колеса машин и детали механизмов и т. д.

На рисунке 149, а изображен однородный диск, который может вращаться вокруг закрепленной оси, проходящей через его центр — точку О. Если подвесить к нему тело в точке А, то диск будет находиться в равновесии.

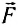
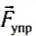
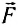
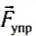
Естественно, что действующая сила будет уравновешиваться силой упругости со стороны оси вращения. Если подвесить тело в точке В, то равновесие тоже не нарушится. Отсюда можно сделать вывод, что точку приложения силы натяжения можно переносить вдоль линии действия силы. При этом силы и лежат на одной прямой.

Если же прямая, на которой лежит вектор силы 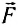, не проходит через ось вращения, то эта сила не может быть уравновешена силой упругости оси, и тело поворачивается вокруг нее (рис. 149, б).

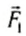
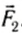
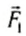
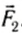
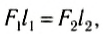
На рисунке 149, в изображен тот же диск, на который действуют две силы и . Численные значения этих сил определяются динамометрами. Сила вращает диск против часовой стрелки, а сила — по часовой стрелке. Диск не будет вращаться, если выполняется условие:
(2)

где l₁ и l₂ — кратчайшие расстояния от оси вращения до прямых, на которых лежат векторы сил и .

Итак, мы получили известное вам из курса физики 8-го класса условие равновесия рычага.

Кратчайшее расстояние от оси вращения до линии действия силы называется плечом силы, а произведение модуля силы F на плечо l называется моментом силы М:
M = Fl (3)

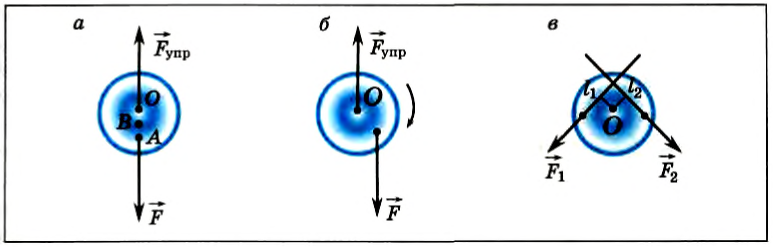
Рис. 149

Следовательно, равенство (2) означает равенство моментов сил F₁ и F₂. Но момент силы F₁ вращает диск против часовой стрелки, а момент силы F₂ — по часовой стрелке. Поэтому им нужно приписать различные знаки. Обычно положительным считают момент силы, вызывающий вращение по часовой стрелке, а отрицательным — момент силы, вызывающий вращение против часовой стрелки.

Итак, вторым условием равновесия тела является правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу, относительно этой оси равна нулю.

Таким образом, тело будет находиться в равновесии, если выполняются два условия: (1) и (4). Например, доска, изображенная на рисунке 150, находится в равновесии.

Рис. 150

Главные выводы:

Условия равновесия тел

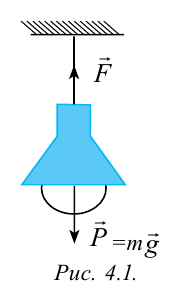
Рассмотрим силы, действующие на подвешенную к потолку лампу (рис. 4.1). Для начала вспомним изученное в 6-м классе понятие «центр масс» тела.

Центр масс – это воображаемая точка, в которой воплощена вся масса тела.
Исходя из этого будем считать, что силы, действующие на тело, приложены к центру масс. На подвешенную лампу действует направленная вниз сила тяжести . При этом туго натягивается удерживающая ее нить. Возникающая в нити сила натяжения и сила тяжести действуют вдоль одной прямой линии, которая проходит через центр массы и направлены противоположно. Эти силы равны по модулям. Если эти силы сложить по правилу сложения векторов, то результирующая сила становится равной нулю. Поэтому лампа остается в положении равновесия.

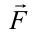
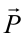
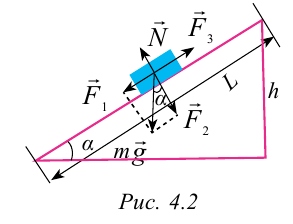
Рассмотрим случай, когда тело покоится в равновесии на наклонной плоскости (рис. 4.2). Рассмотрим действующие относительно центра масс силы в этом случае. На тело действует сила тяжести .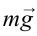
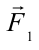
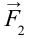
Эту силу разделим на составляющие: и .

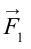
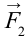
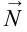
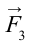
При этом сила стремится сдвинуть тело вниз по наклонной плоскости, сила представляет силу давления на площадь наклонной плоскости. Эта сила приводит к образованию силы реакции на тело со стороны наклонной плоскости. Также на тело действует сила трения в противоположном относительно скольжения направлении.

В этом случае векторная сумма всех действующих сил тоже будет равна нулю.

Исходя из вышесказанного можно сделать следующие выводы:
Для того чтобы тело или система тел, не имеющие вращения оси, остались в равновесии, векторная сумма всех действующих на них сил должна быть равна нулю.

Виды равновесия

Если некое тело находится в состоянии равновесия, это не означает, что оно постоянно будет находиться в таком состоянии (рис. 4.3). В реальных условиях тело подвергается неожиданным воздействиям извне, которые невозможно избежать. Главное, что нужно знать – останется ли тело после такого воздействия в равновесии или равновесие будет нарушено. Для этого необходимо учесть направление результирующей силы внешнего воздействия. В зависимости от направления результирующей силы различают три вида равновесия.

Устойчивое равновесие

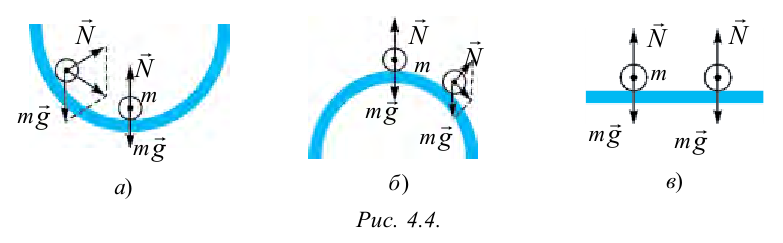
При выведении тела из положения равновесия возникают силы, возвращающие тело в прежнее положение, это называется устойчивым равновесием (рис. 4.4а). В данном случае, при небольшом смещении шарика, лежащего на дне сферического углубления, равнодействующая сила возвращает его в положение равновесия.

Неустойчивое равновесие

При выведении тела из положения равновесия возникают силы, удаляющие его от положения равновесия, это называется неустойчивым равновесием (рис. 4.4б). В данном случае шарик находится в верхней точке выпуклой сферической поверхности. При небольшом смещении из положения равновесия равнодействующая сила действующих на него сил удаляет его еще дальше от состояния равновесия.

Безразличное равновесие

Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называется безразличным равновесием (рисунок 4.4в). Если приложить силу к шарику, находящемуся на горизонтальной поверхности, то он переместится на другое место.

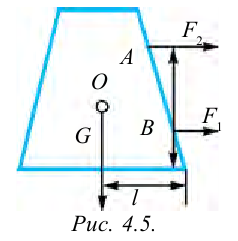
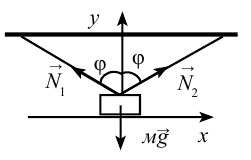
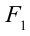
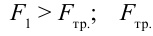
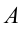
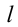
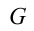
Если на тело, показанное на рисунке 4.5 действует сила в точке ниже центра тяжести ( – сила трения), тело приходит в поступательное движение. Не меняя величину силы, приложим ее к точке , при этом тело начинает наклоняться. Начинает уменьшаться расстояние между крайними точками нижнего основания контура и вектором, направленным вниз из центра тяжести. Если продолжить прикладывать силу, вектор выйдет за пределы контура тела и оно опрокинется.

Таким образом, равновесие тела зависит от:

Образец решения задачи

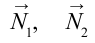
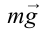
Согласно чертежу, действующие на груз силы и пересекаются в одной точке.
Следовательно, условие равновесия определяется двумя уравнениями:

После внесения математических изменений получим: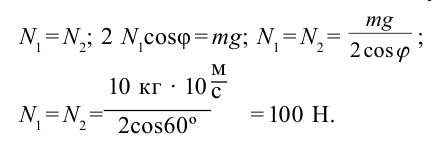

Ответ: 100 Н.

Определение условия равновесия тела

По I закону Ньютона, нахождение тела в состоянии равновесия означает, что оно находится в покое или движется прямолинейно и равномерно в инерциальной системе отсчета. Ознакомимся с условиями, при выполнении которых тело остается в состоянии равновесия.

Равновесие тела при поступательном движении

Для нахождения тела в состоянии равновесия при его поступательном движении равнодействующая сила (геометрическая сумма всех действующих на тело сил), прикладываемая к телу, должна быть равна нулю:

Если геометрическая сумма сил равна нулю, то и сумма проекций этих сил на произвольную координатную ось равна нулю:

Равновесие тела с неподвижной осью вращения

Тело с неподвижной осью вращения находится в равновесии, если алгебраическая сумма моментов действующих на него сил относительно оси вращения равна нулю:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Условия равновесия тел — виды, формулы и примеры

Раздел механики, изучающий условия равновесия тел, называют статикой. Методы науки используются в самых различных областях деятельности человека. Архитекторы и инженеры рассчитывают силы, действующие на всевозможные конструкции, знание о поведении мышц позволяет лечить травмы. Поэтому важным в физике является понимание условий, обеспечивающих телу состояние покоя, умение расчёта действующих сил. При этом единого способа решения задач не существует.

Общие сведения

Статика — это наука, изучающая силы, при которых положение тела не изменяется в пространстве. Такая ситуация называется равновесием. Особенность покоящихся тел в том, что в таком состоянии они не обладают ускорением и скоростью, а результирующая сила и момент равны нулю. Поэтому и кажется, что на тело не оказывается никакого воздействия, но на самом деле это не так.

В общем смысле под равновесием понимают состояние, которое может сохраняться сколько угодно долго, если нет внешних воздействий. Это утверждение справедливо для любого вида состояния покоя. Например, механического, теплового, экономического, политического и тому подобного.

В механике состояние движения физической точки описывает скорость. Если она не изменяется, то параметр всегда постоянный. Значит, под механическим равновесием можно понимать состояние прямолинейного равномерного движения. Кроме этого, при определённых условиях к нему можно отнести и обращение. Например, вращающееся колесо, которое крутится на оси без учёта сил трения.

При воздействии различных сил на материальную точку объект может вести себя трояко. В соответствии с этим различают три вида реакции физического тела на попытку вывести его из этого положения:

Следует отметить, что для того чтобы узнать, какой вид равновесия присущ ситуации, необходимо вывести объект из положения покоя. При этом первостепенной задачей статики является изучение условий, которые приводят к одному из трёх состояний тела, и их математическое описание.

Центр тяжести и условия равновесия

Простейшим случаем, при котором материальная точка находится в равновесии, будет тот, когда нет вращения, а размерами тела можно пренебречь. В этом случае ускорение равняется нулю: a = 0. Выяснить условия равновесия значит определить действующие силы. Согласно второму закону Ньютона, их равнодействующую можно найти из произведения массы на ускорение: F = m * a. Отсюда следует, что в состоянии покоя F = 0.

Реальное тело имеет определённые размеры. Чтобы определить для такого случая условие, необходимо рассмотреть самый простой вид движения — поступательное. Им называют перемещение, при котором все точки в теле двигаются одинаково, то есть с одной и той же скоростью. А это значит, что ускорения для всех его частиц будет постоянным и равняться нулю.

Пусть имеется горизонтальная поверхность, на которой находится, например, тележка. Через неё можно провести условную прямую под любым наклоном к горизонту. Места пересечения контуров тела с построенной линией будут точками A и B. К любой из них можно приложить силу F. Тележка начнёт двигаться. Эту силу можно перенести вдоль линии к другой точке, не изменяя направления, то есть сменить место приложения. В результате никаких изменений не произойдёт.

Но предыдущих двух условий мало, чтобы можно было сформулировать достаточные условия. Например, пусть есть карандаш, лежащий на столе.

Сумма действующих на него сил равняется нулю, но при этом он может вращаться. Значит, важным условием должно быть отсутствие углового ускорения. Другими словами, состояние, при котором момент внешних сил равен нулю.

Таким образом, если тело находится в равновесии, для него должны выполняться три условия:

Перечисленные условия являются необходимыми для нахождения тела в состоянии равновесия. Составив систему из уравнений, можно решать задачи с тремя неизвестными, что часто оказывается более чем достаточно, особенно для школьной программы.

Закреплённая ось вращения

Объект не будет вращаться, если равнодействующая приложенных к нему сил будет равняться нулю. Пусть имеется тело эллипсоидной формы. Чтобы оно не перемещалось поступательно, необходимо добиться одинакового движения точек.

В предмете можно сделать отверстие, которое будет обозначать ось вращения. Тогда центры перемещения точек находятся на этой линии.

К произвольно взятому месту A можно приложить силу F. Тело начнёт поворачиваться до тех пор, пока не наступит ситуация, при которой линия действия F начнёт проходить через ось. Тогда вращение прекратится. То есть произойдёт компенсирование реакцией оси. Кроме того, эти два действия не только лежат на одной линии, но и равны по модулю.

Из второго условия равновесия следует, что силу можно перемещать вдоль оси. Если это сделать, то к противоположной точке A окажется приложено две силы. Они будут равны по величине, но противоположны по направлению. Эта пара действует на закреплённую ось, поэтому предмет, необязательно эллипсоидной формы, вращаться не будет.

Таким образом, тело любого размера и массы с закреплённой осью будет находиться в равновесии, если линия действия приложенной к ней силы проходит через ось. Это простая ситуация. Но может случиться так, что на тело будет оказываться воздействия одновременно с нескольких сторон. Причём они будут приложены к разным местам тела. В этом случае, как и в первом, всё равно можно будет подобрать такую силу, которая будет действовать, как все существующие.

Значит, обобщённое определение можно сформулировать так: тело с закреплённой осью вращения будет находиться в равновесии, если линия действия равнодействующей приложенных воздействий проходит через ось.

Но на самом деле этим правилом пользоваться неудобно, так как часто найти общее действие бывает довольно сложно. Поэтому используют плечо силы. Это кратчайшее расстояние до оси вращения. Физически величина равна произведению модуля действия на её плечо и называется моментом. Описывают её формулой: M = F * d, где первый член — модуль, а второй — плечо относительно оси вращения.

За единицу измерения момента принимают ньютон, умноженный на метр (Н * м). Причём эта величина может иметь как положительное, так и отрицательное значение. Выбор знака зависит от направления. Строго требования нет, но в математике вращение по часовой стрелке считают плюсовым, а против — минусовым.

Решение задач

Важно не только знать теоретический материал, но и уметь применять его на практике. Единого метода решения задач в статике не существует. В учебных классах по физике можно встретить плакаты, на которых изображён алгоритм вычислений, когда тело находится в инерциальной системе отсчёта (ИСО). Последовательность действий выглядит так:

Несомненно, самым трудным будет первый шаг. Вот один из примеров среднего уровня сложности. Однородная балка массой 1200 кг представляет собой весы. В конструкции убрали среднюю опору, но поставили две крайних. На балку положили механизм весом 15 тонн. Определить силу, действующую на каждую из вертикальных опор. Учесть, что длина между колонами составляет 20 м, а расстояние от центра до груза равняется пяти метрам.

Вначале следует рассмотреть силы, действующие на концы балки. Они будут равны по величине действиям, с которыми концы главного стержня давят на опоры. Пусть это будет F1 и F2. Сила тяжести балки приложена к центру масс, то есть приходится на середину. Так как условие равновесия для моментов можно записать относительно любой точки, то удобнее взять её в месте приложения F1. Поскольку в этом случае она будет равняться нулю из-за значения плеча, то останется только одна неизвестная — F2.

Таким образом, главное — правильно выбрать ось вращения, тем самым сделать расчёт более простым. Следует отметить, что в инженерии некоторые силы определяют с помощью специальных датчиков напряжения. Например, пьезоэлектрические датчики и тензодатчики. Их крепят как на саму конструкцию, так и на её модель.

Источник