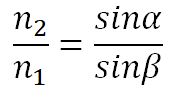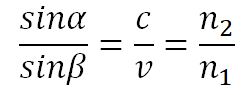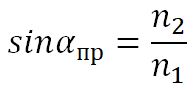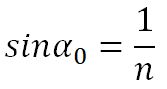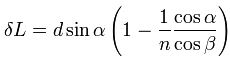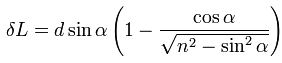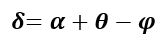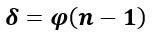в каком случае угол преломления луча равен углу падения

Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Рис. 1. Преломление луча на границе «воздух–среда»

Закон преломления (переход «воздух–среда»).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2 ) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе «среда–воздух»

Закон преломления (общий случай).

Рис. 3.

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4 ). Здесь угол падения меньше угла преломления:

Рис. 4.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

Полное внутреннее отражение.

Рис. 5. Полное внутреннее отражение

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Величину легко найти из закона преломления. Имеем:

Так, для воды предельный угол полного отражения равен:

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

Источник

В каком случае угол преломления луча равен углу падения

Наблюдение преломления света.

На границе двух сред свет меняет направление своего распространения. Часть световой энергии возвращается в первую среду, т. е. происходит отражение света. Если вторая среда прозрачна, то свет частично может пройти через границу сред, также меняя при этом, как правило, направление распространения. Это явление называется преломлением света.

Вследствие преломления наблюдается кажущееся изменение формы предметов, их расположения и размеров. В этом нас могут убедить простые наблюдения. Положим на дно пустого непрозрачного стакана монету или другой небольшой предмет. Подвинем стакан так, чтобы центр монеты, край стакана и глаз находились на одной прямой. Не меняя положения головы, будем наливать в стакан воду. По мере повышения уровня воды дно стакана с монетой как бы приподнимается. Монета, которая ранее была видна лишь частично, теперь будет видна полностью. Установим наклонно карандаш в сосуде с водой.

Если посмотреть на сосуд сбоку, то можно заметить, что часть карандаша, находящаяся в воде, кажется сдвинутой в сторону (рис. 96).

Эти явления объясняются изменением направления лучей на границе двух сред — преломлением света.

Закон преломления света определяет взаимное расположение падающего луча АВ (рис. 97), преломленного DB и перпендикуляра СЕ к поверхности раздела сред, восставленного в точке падения. Угол а называется углом падения, а угол β— углом преломления.

Падающий, отраженный и преломленный лучи нетрудно наблюдать, сделав узкий световой пучок видимым. Ход такого пучка в воздухе можно проследить, если пустить в воздух немного дыма или же поставить экран под небольшим углом к лучу. Преломленный пучок также виден в подкрашенной флюоресцеином воде аквариума (рис. 98).

Вывод закона преломления света. Закон преломления света был установлен опытным путем в XVII веке. Мы его выведем с помощью принципа Гюйгенса.

Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в той и другой среде. Обозначим скорость волны в первой среде через v₁, а во второй — через v_2.

Пусть на плоскую границу раздела двух сред (например, из воздуха в воду) падает плоская световая волна (рис. 99). Волновая поверхность АС перпендикулярна лучам А₁А и В₁В. Поверхности MN сначала достигнет луч А₁А. Луч В₁В достигнет поверхности спустя время

Поэтому в момент, когда вторичная волна в точке В только начнет возбуждаться, волна от точки А уже имеет вид полусферы радиусом

Волновую поверхность преломленной волны можно получить, проведя поверхность, касательную ко всем вторичным волнам во второй среде, центры которых лежат на границе раздела сред. В данном случае это плоскость BD. Она является огибающей вторичных волн.

Угол падения α луча равен углу САВ в треугольнике АВС (стороны одного из этих углов перпендикулярны сторонам другого). Следовательно,

Угол преломления β равен углу ABD треугольника ABD. Поэтому

Разделив почленно (5.2) на (5.3), получим

где n — постоянная величина, не зависящая от угла падения.

Из построения (рис. 99) видно, что падающий луч, луч преломленный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Данное утверждение совместно с уравнением (5.4), согласно которому отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред, представляет собой закон преломления света.

Убедиться в справедливости закона преломления можно экспериментально, измеряя углы падения и преломления и вычисляя отношение их синусов при различных углах падения. Это отношение остается неизменным.

Показатель преломления. Постоянная величина, входящая в закон преломления света, называется относительным показателем преломления или показателем преломления второй среды относительно первой.

Из принципа Гюйгенса не только следует закон преломления, но с помощью этого принципа раскрывается физический смысл показателя преломления. Он равен отношению скоростей света в средах, на границе между которыми происходит преломление:

Если угол преломления β меньше угла падения а, то согласно (5.4) скорость света во второй среде меньше, чем в первой.

Показатель преломления среды относительно вакуума называют абсолютным показателем преломления этой среды. Он равен отношению синуса угла падения к синусу угла преломления при переходе светового луча из вакуума в данную среду.

Пользуясь формулой (5.5), можно выразить относительный показатель преломления через абсолютные показатели преломления n₁ и n₂ первой и второй сред.

Среду с меньшим абсолютным показателем преломления принято называть оптически менее плотной средой.

Абсолютный показатель преломления определяется скоростью распространения света в данной среде, которая зависит от физического состояния среды, т. е. от температуры вещества, его плотности, наличия в нем упругих напряжений. Показатель преломления зависит также и от характеристик самого света. Для красного света он меньше, чем для зеленого, а для зеленого — меньше, чем для фиолетового.

Поэтому в таблицах значений показателей преломления для разных веществ обычно указывается, для какого света приведено данное значение n и в каком состоянии находится среда. Если таких указаний нет, то это означает, что зависимостью от указанных факторов можно пренебречь.

В большинстве случаев приходится рассматривать переход света через границу воздух — твердое тело или воздух — жидкость, а не через границу вакуум — среда. Однако абсолютный показатель преломления n₂ твердого или жидкого вещества отличается от показателя преломления того же вещества относительно воздуха незначительно. Так, абсолютный показатель преломления воздуха при нормальных условиях для желтого света равен приблизительно n₁≈1,000292. Следовательно,

Значения показателей преломления для некоторых веществ относительно воздуха приведены в таблице 2 (данные относятся к желтому свету).

Ход лучей в треугольной призме.

Закон преломления света позволяет рассчитать ход лучей в различных оптических устройствах, например в треугольной призме, изготовленной из стекла или других прозрачных материалов.

На рисунке 100 изображено сечение стеклянной призмы плоскостью, перпендикулярной ее боковым ребрам. Луч в призме отклоняется к основанию, преломляясь на гранях ОА и ОВ. Угол φ между этими гранями называют преломляющим углом призмы. Угол 0 отклонения луча зависит от преломляющего угла призмы ф, показателя преломления n материала призмы и угла падения а. Он может быть вычислен с помощью закона преломления (5.4).

ПОЛНОЕ ОТРАЖЕНИЕ

При прохождении света из оптически менее плотной среды в более плотную, например из воздуха в стекло или воду, v₁ и v₂ согласно закону преломления (5.4) показатель преломления 1. Поэтому а>β (рис. 101, а):

преломленный луч приближается к перпендикуляру к границе раздела сред. Если направить луч света в обратном направлении — из оптически более плотной среды в оптически менее плотную вдоль бывшего преломленного луча (рис. 101, б), то закон преломления запишется так:

Преломленный луч по выходе из оптически более плотной среды пойдет по линии бывшего падающего луча, поэтому а а_о. При падении света на границу двух сред световой луч, как об этом уже упоминалось, частично преломляется, а частично отражается от нее. При а>a₀ преломление света невозможно. Значит, луч должен полностью отразиться. Это явление и называется полным отражением света.

Для наблюдения полного отражения можно использовать стеклянный полуцилиндр с матовой задней поверхностью. Полуцилиндр закрепляют на диске так, чтобы середина плоской поверхности полуцилиндра совпадала с центром диска (рис. 103). Узкий пучок света от осветителя направляют снизу на боковую поверхность полуцилиндра перпендикулярно его поверхности. На этой поверхности луч не преломляется. На плоской поверхности луч частично преломляется и частично отражается. Отражение происходит в соответствии с законом отражения, а преломление — в соответствии с законом преломления (5.4).

Если увеличивать угол падения, то можно заметить, что яркость (и следовательно, энергия) отраженного пучка растет, в то время как яркость (энергия) преломленного пучка падает. Особенно быстро убывает энергия преломленного пучка, когда угол преломления приближается к 90°. Наконец, когда угол падения становится таким, что преломленный пучок идет вдоль границы раздела (см. рис. 102), доля отраженной энергии составляет почти 100%. Повернем осветитель, сделав угол падения а большим а_о. Мы увидим, что преломленный пучок исчез и весь свет отражается от границы раздела, т. е. происходит полное отражение света.

На рисунке 104 изображен пучок лучей от источника, помещенного в воде недалеко от ее поверхности. Большая интенсивность света показана большей толщиной линии, изображающей соответствующий луч.

Угол падения а_о, соответствующий углу преломления 90°, называют предельным углом полного отражения

При sin β= 1 формула (5.8) при нимает вид

Из этого равенства и может быть найдено значение предельного угла полного отражения а_о. Для воды (n = 1,33) он оказывается равным 48°35′, для стекла (n =1,5) он принимает значение 41°51′, а для алмаза (n— 2,42) этот угол составляет 24°40′. Во всех случаях второй средой является воздух.

Явление полного отражения легко наблюдать на простом опыте. Нальем в стакан воду и поднимем его несколько выше уровня глаз. Поверхность воды при рассматривании ее снизу сквозь стенку кажется блестящей, словно посеребренной вследствие полного отражения света.

Полное отражение используют в так называемой волоконной оптике для передачи света и изображения по пучкам прозрачных гибких волокон — световодов. Световод представляет собой стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления. За счет многократного полного отражения свет может быть направлен по любому (прямому или изогнутому) пути (рис. 105). Волокна набираются в жгуты. При этом по каждому из волокон передается какой-нибудь элемент изображения (рис. 106). Жгуты из волокон используются, например, в медицине для исследования внутренних органов.

По мере улучшения технологии изготовления длинных пучков волокон— световодов все шире начинает применяться связь (в том числе и телевизионная) с помощью световых лучей.

Трехсантиметровые волны: закон отражения (металл)

Полное внутреннее отражение

Источник

В каком случае угол преломления луча равен углу падения

Каждая точка, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

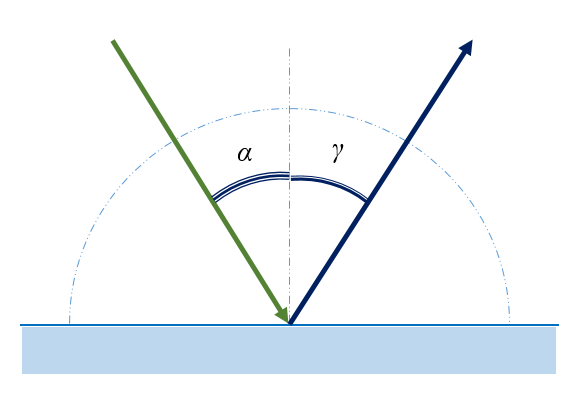
α = γ

Вывод на основе принципа Гюйгенса:

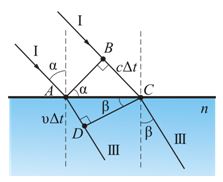
Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела двух сред. Когда фронт волны АВ достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну.

Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен: υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны – лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол падения α равен углу отражения γ.

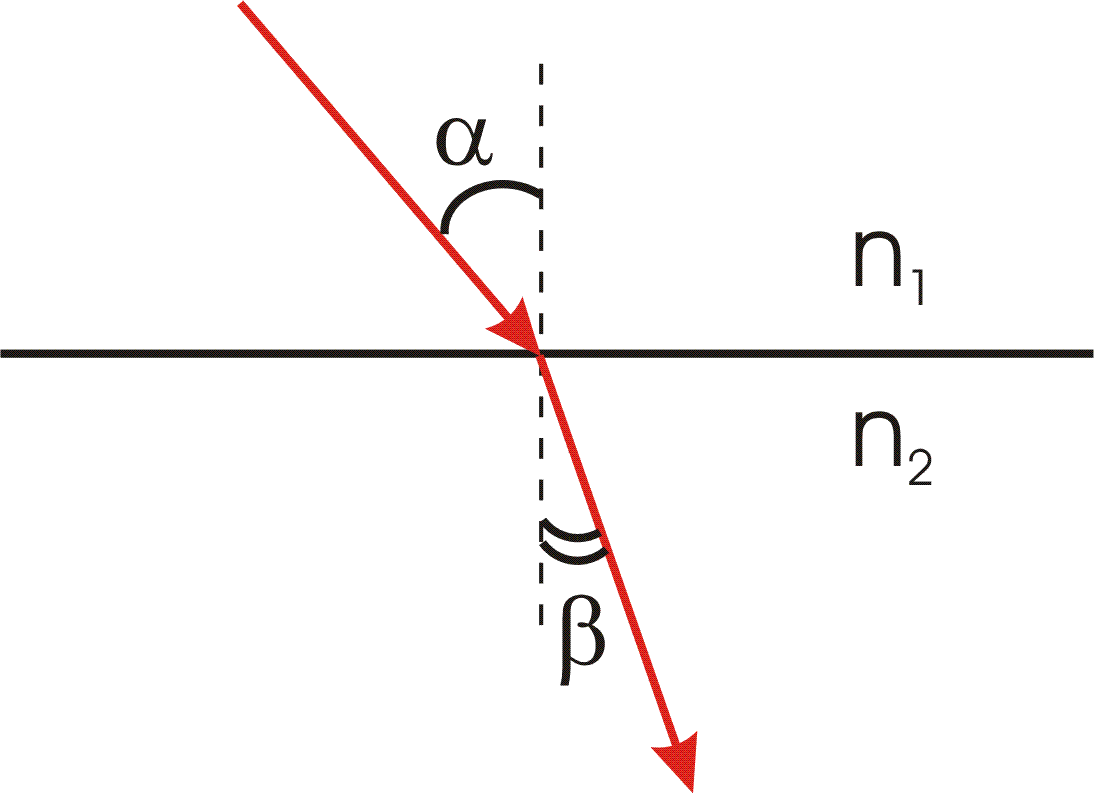
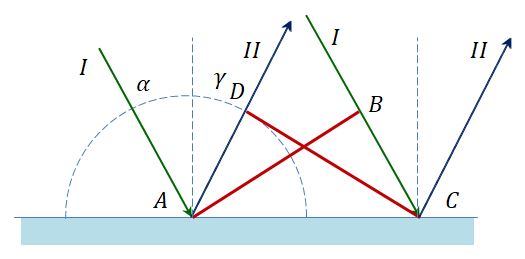
Вывод закона преломления. Предположим, что плоская волна (фронт волны АВ), распространяющаяся в вакууме вдоль направления I со скоростью с, падает на границу раздела со средой, в которой скорость ее распространения равна v.

Пусть время, затрачиваемое волной для прохождения пути ВС, равно Δt. Тогда ВС = сΔt. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью u, достигнет точек полусферы, радиус которой AD = vΔt. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения – лучом III. Из рис. видно, что

, т.е. .

Отсюда следует закон Снелиуса:

П ринцип Ферма : свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время.

Покажем применение этого принципа к решению той же задачи о преломлении света.

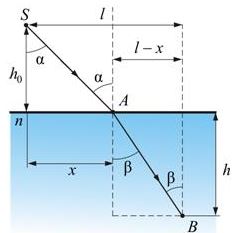
Луч от источника света S, расположенного в вакууме идет до точки В, расположенной в некоторой среде за границей раздела

В каждой среде кратчайшим путем будут прямые SA и AB. Точку A охарактеризуем расстоянием x от перпендикуляра, опущенного из источника на границу раздела. Определим время, затраченное на прохождение пути SAB:

.

Для нахождения минимума найдем первую производную от τ по х и приравняем ее к нулю:

,

отсюда приходим к тому же выражению, что получено исходя из принципа Гюйгенса: .

Следствия из принципа Ферма:

1. Обратимость световых лучей: если обратить луч III, заставив его падать на границу раздела под углом β, то преломленный луч в первой среде будет распространяться под углом α, т. е. пойдет в обратном направлении вдоль луча I.

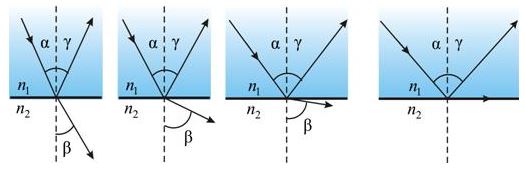
2. Если свет распространяется из среды с большим показателем преломления n₁ (оптически более плотной) в среду с меньшим показателем преломления n₂ (оптически менее плотной) ( n₁ > n₂ ), например из стекла в воздух, то, согласно закону преломления, преломленный луч удаляется от нормали и угол преломления β больше, чем угол падения α:

3. С увеличением угла падения увеличивается угол преломления, до тех пор, пока при некотором угле падения (α = α_пр) угол преломления не окажется равным π/2.

Полное отражение

По мере приближения угла падения к предельному, интенсивность преломленного луча уменьшается, а отраженного – растет.

Преломление света в плоскопараллельной пластине

Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения.

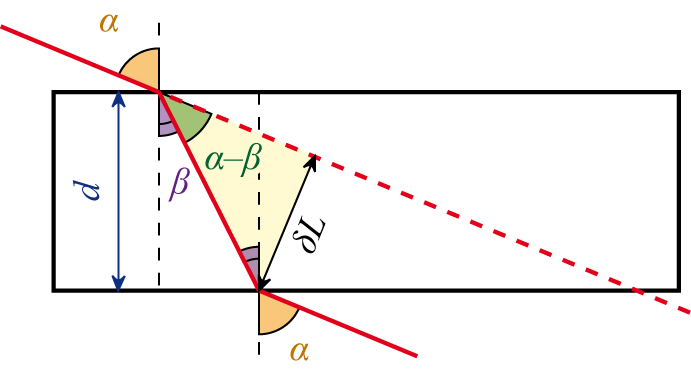
Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величину δL относительно исходного луча

Величина смещения в плоскопараллельной пластине

Величина сдвига луча света δL зависит:

C увеличением любого из этих параметров смещение луча света увеличивается.

Смещение луча можно выразить через угол падения

Из этого выражения видно, что величина смещения луча в пластине зависит от угла падения, толщины пластины и показателя преломления. Из формулы видно, что отклонения луча не происходит, если:

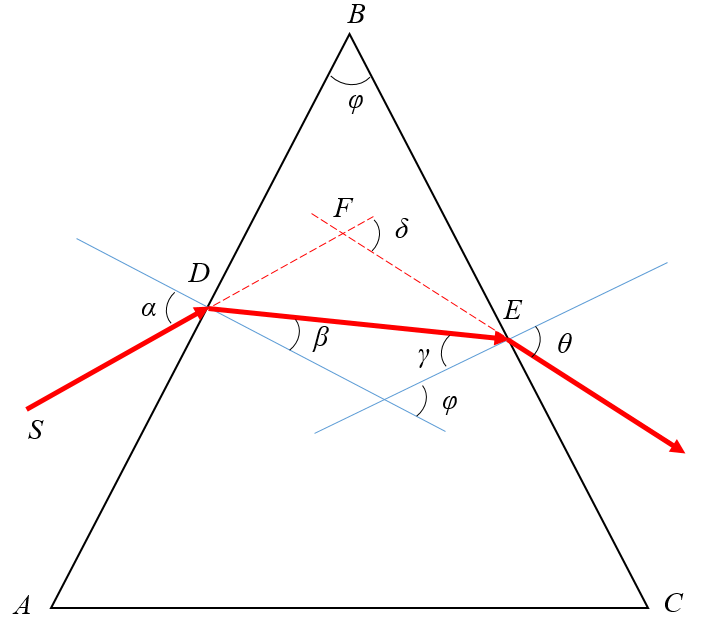
Ход луча через треугольную призму

Призма — оптический элемент из прозрачного материала (например, оптического стекла) в форме геометрического тела — призмы, имеющий плоские полированные грани, через которые входит и выходит свет. Свет в призме преломляется. Важнейшей характеристикой призмы является показатель преломления материала, из которого она изготовлена.

На призму из точки S падает луч света. Испытав 2 преломления, он выходит с отклонением на угол δ, который называется угол отклонения луча. Угол при вершине призмы АВС – φ называется преломляющим углом.

Если световой луч падает на преломляющую грань призмы под малым углом (практически перпендикулярно преломляющей грани призмы), то угол отклонения луча призмой определяется формулой

Если призма сделана из материала, показатель преломления которого больше, чем у среды, в которой находится призма, отклонение лучей происходит к основанию призмы.

Лучи различного цвета (различной частоты или длины волны) отклоняются призмой по-разному. В случае нормальной дисперсии (показатель преломления материала тем выше, чем больше частота светового излучения) призма наиболее сильно отклоняет фиолетовые лучи; наименее — красные.

Источник