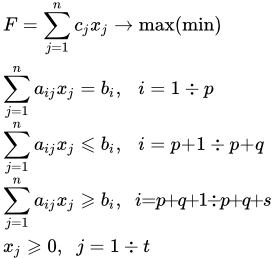в каком случае задача линейного программирования решений не имеет

Основы линейного программирования

Задача линейного программирования

Переменные задачи часто записывают в виде n-мерного вектора:
.

Система ограничений (1.2) может состоять из равенств
,
и неравенств обоих знаков:
, или
.

В системе ограничений особо выделяют ограничения, связанные с не отрицательностью некоторых переменных (1.3), которые являются следствием физических свойств величин, описываемых этими переменными.

Различные формы задач ЛП

Теорема
Любую общую задачу линейного программирования (1.1) – (1.3) можно привести к каноническому виду (1.4). А любую задачу в канонической форме можно привести к любой из задач в симметричной форме (1.5) или (1.6).

При таких преобразованиях переменные задач могут не совпадать. Могут вводиться новые переменные, а также переменные одной из задач могут линейно выражаться через переменные той же задачи, записанной в другой форме.

Дополнительная переменная (вспомогательная переменная) – это переменная, которая вводится для преобразования неравенства в равенство. Дополнительную переменную также называют вспомогательной переменной. Например, неравенство

переводится в равенство, введением дополнительной неотрицательной переменной :
.

Графический метод решения

Свойства решений задач линейного программирования (ЛП) наглядно демонстрирует графический метод решения.

Решение задачи линейного программирования графическим методом.

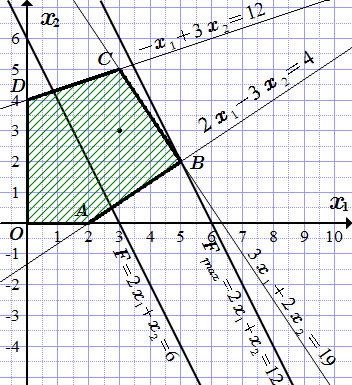
Графическим методом можно решить задачу, если она имеет две переменные, или ее можно привести к задаче с двумя переменными.

Свойства решений задач ЛП

Далее приводим более строгую трактовку этих рассуждений.

Теорема о выпуклости ОДР
Область допустимых решений задачи линейного программирования является выпуклым множеством.

Теорема об оптимальном решении
Если задача линейного программирования имеет единственное решение, то оптимальный план является угловой точкой ОДР. Если существует несколько оптимальных планов, то в него входят две или более угловых точек, и любая выпуклая линейная комбинация этих угловых точек также является оптимальным планом. То есть задача имеет бесконечно много решений.

Выпуклое множество Возьмем две произвольные точки, принадлежащие некоторому множеству. Если все точки отрезка, соединяющего эти точки, принадлежат этому множеству, то такое множество называется выпуклым. Угловая (крайняя) точка выпуклого множества – это точка, через которую нельзя провести отрезок так, чтобы она была внутренней точкой отрезка, концы которого принадлежат множеству. Угловую точку также называют крайней точкой. Опорный план – это план (допустимое решение), который является угловой точкой (вершиной многогранника) области допустимых решений.

Поскольку в задачах линейного программирования система ограничений содержит конечное число неравенств, то ОДР является многогранником. Тогда угловые точки ОДР являются вершинами многогранника.

Лемма
Оптимальный план задачи линейного программирования является опорным планом, и может быть выбран из совокупности ее опорных планов.

Теорема
Угловая точка ОДР (1.2) – (1.3) является решением системы из n уравнений, полученной из (1.2) – (1.3), вычеркиванием части неравенств, и заменой оставшихся неравенств равенствами.

Задачи линейного программирования в канонической форме

Выше мы указали, что оптимальный план является угловой точкой ОДР. Но угловая точка получается из системы ограничений, заменой части неравенств равенствами, чтобы в результате получилась система из n линейно независимых уравнений. Решая эту систему, можно найти координаты угловой точки.

Если в рассматриваемой угловой точке план не вырожден, то в ней имеется только один набор базисных переменных. Если же план вырожден, то в этой точке имеется два или более набора базисных переменных.

Теорема о числе базисных переменных
При решении задачи линейного программирования в канонической форме ⇑, в любом опорном плане имеется r базисных переменных ⇑. Отсюда следует, что в опорном плане как минимум переменных равны нулю. Здесь n – число переменных; r – ранг матрицы системы ограничений (1.4), из которой определяются значения базисных переменных.

Методы решения задач

Графический метод

Метод перебора вершин

В этом методе мы используем тот факт, что оптимальный план является угловой точкой ОДР. А если задача имеет множество решений, то среди них имеются угловые точки.

В методе перебора вершин мы находим все угловые точки, и вычисляем в них значения целевой функции. Далее, из этих значений, определяем наибольшее или наименьшее значение целевой функции.

Решение задачи

Но мы применим более общий метод, который работает при любом числе переменных, а не только для двух.

В этой задаче переменных. Система ограничений (П.2) содержит 3 линейно независимых уравнения. Поэтому в произвольной угловой точке имеется свободные переменные, и 3 базисные. Перебираем все возможные сочетания свободных переменных, приравниваем их к нулю, и, решая систему (П.2), определяем значения базисных переменных.

Итак, мы нашли все угловые точки ОДР. Находим в них значения целевой функции.
;
;
;
;
.

Симплексный метод

Для решения задачи симплексным методом, сначала задачу приводят к канонической форме. Далее выбирают любой опорный план с некоторым набором базисных переменных. Потом определяют свободную переменную, которую нужно включить в базис, чтобы при такой замене произошло наибольшее увеличение целевой функции. Определяют переменную, выходящую из базиса и с помощью линейных преобразований, совершают переход к новым базисным переменным. В результате получают новый план, значение целевой функции которого ближе к экстремальному. Процесс повторяют до тех пор, пока целевая функция не достигнет экстремального значения.

В геометрической интерпретации это означает следующее.
1. Вначале мы выбираем любую вершину многогранника ОДР.
2. Добавляя в базис новую переменную, выбираем направление до смежной вершины вдоль ребра многогранника, двигаясь по которому целевая функция наиболее быстро возрастает.
3. Переходим на новую вершину по выбранному в пункте 2 направлению, исключая из базиса одну из переменных.
4. Повторяем пункты 2 и 3, пока не достигнем экстремума.

Решение задачи

4. Повторяем шаги 2 и 3.

6. Повторяем шаги 4 и 5.

Транспортная задача

Транспортную задачу можно решить симплексным методом. Однако имеются методы, которые позволяют получить решение другими, как правило, более легкими способами, используя специфичный вид системы ограничений (Т.2) – (Т.3). Одним из таких методов является метод потенциалов. В нем, как и в симплексном методе ⇑, используется метод последовательного улучшения плана. Мы кратко рассмотрим применение этого метода на примере решения простой транспортной задачи.

Решение транспортной задачи методом потенциалов

Вначале нужно подсчитать суммы мощностей поставщиков и потребителей. Если сумма мощностей поставщиков равна сумме мощностей потребителей, то такая задача называется задачей с правильным балансом, или задачей с закрытой моделью. Задача, в которой суммы мощностей поставщиков и потребителей не совпадают, называется задачей с неправильным балансом, или задачей с открытой моделью. Если у задачи открытая модель, то ее сначала нужно привести к закрытой модели, добавлением фиктивного поставщика или потребителя с нулевыми стоимостями перевозок. В нашем случае, сумма мощностей поставщиков равна сумме мощностей потребителей:
.
Модель закрытая, задачу можно решать методом потенциалов.

Задача имеет неотрицательных переменных:
.

Применяем метод последовательного улучшения плана.

Метод северо-западного угла

1. Вначале нам нужно найти любой опорный план, удовлетворяющий системе ограничений (Т.6) и условию не отрицательности переменных. Существует несколько методов, позволяющих это сделать. Мы применим метод северо-западного угла.

Теперь нам нужно вычеркнуть либо первую строку, либо первый столбец. В нашем случае, как первый поставщик, так и первый потребитель исчерпали свои мощности. Однако вычеркнуть мы можем только одну строку или один столбец. Вместе их вычеркнуть нельзя. Вычеркиваем по своему усмотрению первую строку.

Заполняем верхнюю левую ячейку предыдущей таблицы, и вычеркиваем первый столбец.

Первый опорный план.

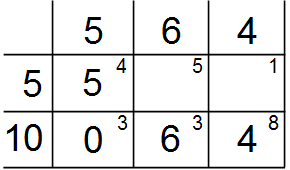
Определение потенциалов

Находим оценки свободных клеток (то есть оценки свободных переменных) по формуле:
.

.

Переход к новому базису

Чтобы перейти к новому базису, в симплексном методе, мы выполняли линейные преобразования над системой ограничений. В транспортной задаче переход выполняется с помощью цикла.

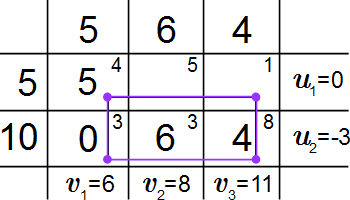
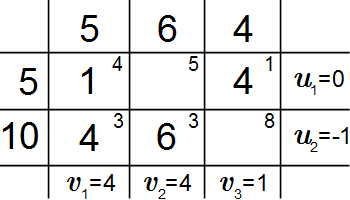
Цикл с начальной вершиной в заданной пустой клетке – это ломаная, все вершины которой расположены в занятых клетках, кроме одной начальной вершины. И при этом две соседние вершины цикла расположены или в одной строке, или в одном столбце. Потенциалы и контур клетки (1,3).

Второй опорный план.

Определение потенциалов нового плана

Находим оценки свободных клеток по формуле:
.

.

Поскольку отрицательных оценок нет, то план оптимален.

Использованная литература:
С. Гасс. Линейное программирование (методы и приложения). Москва, «Государственное издательство физико-математической литературы», 1961.
Общий курс высшей математики для экономистов. Под общей редакцией В. И. Ермакова. Москва, «ИНФРА-М», 2007.
К. Н. Лунгу. Линейное программирование. Руководство к решению задач. Москва, «ФИЗМАТЛИТ», 2005.
Д. Б. Юдин, Е. Г. Гольштейн. Задачи и методы линейного программирования. Москва, «Советское радио», 1961.

Источник

Тест по предмету «Методы оптимальных решений» с ответами

Нет времени или сил пройти тест онлайн? Поможем сдать тест дистанционно для любого учебного заведения: подробности.

Тест по методам оптимальных решений онлайн

Вопрос 1. Каким образом вводятся переменные двойственной задачи, соответствующие ограничениям-уравнениям прямой задачи?

Вопрос 2. Каким образом можно избавиться от уравнений в системе ограничений?

Вопрос 3. При построении двойственной задачи к задаче линейного программирования в стандартной форме вводится столько основных переменных, сколько в прямой задаче.

Вопрос 4. Какая переменная выходит из базиса при преобразовании симплексной таблицы?

Вопрос 5. Что такое критерий эффективности операции?

Вопрос 7. В матричной форме можно записать.

Вопрос 8. Что показывают «теневые цены» (основные переменные двойственной задачи) в линейной задаче производственного планирования?

Вопрос 12. В каком случае задача математического программирования является линейной?

Вопрос 13. Чему равны не базисные переменные в опорном плане задачи линейного программирования?

Вопрос 14. Если оптимальное значение искусственной переменной при решении задачи методом искусственного базиса равно положительному числу, то.

Вопрос 17. Что такое оптимум задачи линейного программирования?

Вопрос 18. В чем заключается критерий оптимальности симплексной таблицы?

Вопрос 19. Все точки, удовлетворяющие уравнению системы ограничений задачи линейного программирования с двумя переменными, образуют на плоскости.

Вопрос 20. Каким образом строятся ограничения двойственной задачи, соответствующие переменным прямой задачи, не ограниченным по своему знаку?

Вопрос 23. Если оптимальное значение искусственной переменной при решении задачи методом искусственного базиса равно отрицательному числу,

Вопрос 24. Что такое оптимальный план задачи линейного программирования?

Вопрос 27. В каком случае точка на отрезке между оптимальными планами задачи линейного программирования тоже будет оптимальным планом (задача не целочисленная)?

Вопрос 28. Сколько допустимых планов может иметь задача линейного программирования (не целочисленная)?

Вопрос 29. Что такое неограниченная область допустимых планов задачи линейного программирования?

Вопрос 30. Что такое допустимый план задачи линейного программирования?

Вопрос 31. Если задача линейного программирования разрешима, в каком случае будет разрешима двойственная к ней задача?

Вопрос 32. В каком направлении сдвигают линию уровня целевой функции при решении задачи линейного программирования на максимум?

Вопрос 33. Сколько оптимальных планов может иметь задача линейного программирования (не целочисленная)?

Вопрос 34. Каким образом можно избавиться от не ограниченных по знаку переменных в системе ограничений?

Вопрос 35. Какое из приведенных ниже утверждений о разрешимости сопряженных задач является НЕ верным?

Вопрос 36. На графике оптимальный план задачи линейного программирования с двумя переменными представляет собой.

Вопрос 37. В чем заключается критерий допустимости симплексной таблицы?

Вопрос 38. При построении двойственной задачи к задаче линейного программирования в стандартной форме строится столько ограничений, сколько в прямой задаче.

Вопрос 39. Каким образом строится целевая функция расширенной задачи при использовании двухэтапного симплекс-метода?

Вопрос 40. Какая переменная входит в базис при преобразовании симплексной таблицы?

Источник

СДАЛ / Математика высшая / Математика 1 и второй / Архивные вопросы и решения / Вся математика по темам / 1.1 Математические модели и методы

Что называется экономико-математической моделью:

упрощенные и формально описанные экономические явления

схема работы хозяйственной единицы

любой, формально описанный процесс

Что является математической структурой экономической модели

символические обозначения для учитываемых характеристик экономических объектов и формализованные отношения между ними

формальное описание работы предприятия

Насколько точно экономическая модель описывает реальную действительность

любая экономическая модель адекватно описывает действительность

экономические модели не могут описать реальные экономические процессы и, следовательно, их нельзя применять на практике

любая экономическая модель абстрактна и, следовательно, неполна

все зависит от качества построения модели

По учету фактора времени модели могут делиться на:

динамические и стохастические

статические и динамические

стохастические и детерминированные

теоретические и прикладные

Экзогенными переменными называются:

все параметры модели

переменные, которые задаются вне модели, т.е заранее известны;

переменные, которые определяются в ходе вычислений в модели

любые переменные модели

всякое мероприятие, объединенное единым замыслом и направленным к достижению какой-то цели

любое произведенное действие

любое действие, связанное с управлением предприятия

применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности

Решением в исследовании операций называется:

выбор из рада возможностей, имеющихся у организатора

решение экономических задач

выбор из рада возможностей, используя тот или иной математический аппарат

решение, принимаемое управляющим

Существуют ли общие способы построения экономико-математических моделей?

да, существуют специальные алгоритмы

построение модели зависит от конкретной ситуации

все экономико-математические модели являются стандартными и уже построенными

экономико-математическую модель вообще нельзя построить

Какую проблему позволяют решать обратные задачи исследования операций?

исходя из значения показателя эффективности выбирается решение

если в заданных условиях мы приме какое-то решение хХ, то чему будет равен показатель эффективности

находят показатель эффективности

как выбрать решение х, чтобы показатель эффективности был оптимальным

Какие задачи называются задачами математического программирования?

все задачи, в которых функция оптимизируется

задачи оптимизации функции, при ограничениях, наложенных на переменные

все задачи, в которых переменные ограничены

задачи, в которых нужно решить системы уравнений или неравенств

Какая задача называется задачей линейного программирования?

Любая задача математического программирования

задача, в которой ограничения линейны

задача математического программирования, в которой функция и ограничения линейны

любая задача, где есть линейная функция

В каком случае задачу линейного программирования можно решать графически?

если в задаче 2 переменных

любую задачу линейного программирования можно решать графически

если ограничения заданы равенствами

если ограничения заданны неравенствами

Что является областью допустимых решений?

все решения уравнения целевой функции

область допустимых решений может быть любой

решение системы ограничений

первая четверть координатной плоскости

В каком случае задача линейного программирования решений не имеет?

область допустимых решений не ограничена;

все ограничения в виде равенств

система ограничений не совместна

целевая функция не пересекает область допустимых решений

Какую задачу линейного программирования можно привести к каноническому виду?

если ограничения неравенствами имеют знак 

если ограничения неравенствами имеют знак 

привести никакую задачу к каноническому виду нельзя, она должна быть заранее задана в каноническом виде

Сколько базисных переменных имеет система из m уравнений с n неизвестными (n>m)?

Чему равны не базисные переменные при решении задачи линейного программирования симплекс-методом?

они выражаются через базисные переменные

они равны столбцу свободных членов

их значения могут быть любыми

В каком случае в задаче линейного программирования вводятся искусственные переменные?

когда начальное базисное решение не допустимое

если ограничения неравенствами 

если ограничения неравенствами .

Каким методом можно найти начальное решений транспортной задачи?

методом северо-западного угла

Какая транспортная модель называется сбалансированной (закрытой)?

когда продукции потребляется больше, чем производится.

когда продукции производится больше, чем потребляется

когда продукции производится столько же, сколько потребляется

любая транспортная модель

Задачи поиска экстремума линейных функций с линейными неравенствами ограничений называют…

Задачами нелинейного программирования.

Задачами линейного программирования.

Обязательным условием формализованного представления задачи линейного программирования является …

Целочисленность управляемых переменных.

Отрицательность управляемых переменных.

Вещественность управляемых переменных.

Комплексное представление управляемых переменных.

Экономическая интерпретация целевой функции в задаче линейного программирования заключается в …

Моделировании эластичности спроса.

Моделировании некоторых ограничений производства.

Моделировании динамики развития объекта управления.

Моделировании эластичности предложения.

Моделировании суммарной прибыли субъекта операции.

Значения правых (постоянных) частей неравенств ограничений в задаче линейного программирования экономически интерпретируют как …

Минимально реализуемую прибыль предприятия по соответствующему виду деятельности.

Показатели платежеспособности предприятия.

Максимально реализуемую прибыль предприятия по соответствующему виду деятельности.

Максимальные запасы ресурсов предприятия по соответствующему виду деятельности

Показатели расходов предприятия по месяцам.

Приведение целевой функции к виду, когда в правой части уравнения находится единица.

Приведение целевой функции к виду, когда в правой части уравнения находится минус единица.

Приведение целевой функции к виду, когда в правой части уравнения находится бесконечно большое число.

Приведение целевой функции к виду, когда в правой части уравнения находится отрицательное значение ресурса

Приведение целевой функции к виду, когда в правой части уравнения находится нуль.

Приведение неравенств к виду, когда в правой части стоит нуль.

Приведение неравенств к виду, когда в правой части стоит единица.

Приведение неравенств к равенствам с помощью добавочных переменных.

Приведение неравенств к виду, когда в правой части стоит бесконечно большое число.

Приведение равенств к неравенствам с помощью добавочных переменных.

Графический метод решения задачи линейного программирования применяется, когда …

Количество управляемых переменных более трех.

Необходимо наглядно представить решение задачи в условиях бесконечно большого числа управляемых переменных.

Количество управляемых переменных равно двум.

Другими методами решить данную задачу невозможно.

Градиент целевой функции в задаче линейного программирования…

Моделирует ограничения задачи.

Показывает направление возрастания (убывания) функции.

Показывает угловые точки области допустимых решений.

Всегда должен быть равен нулю.

Всегда должен быть равен бесконечности.

Область допустимых решений в задаче линейного программирования …

Является областью, где действует первое ограничение.

Является областью, где действует последнее ограничение.

Является областью, где объединяются направления и области действий всех ограничений.

Является областью, где пересекаются направления и области действий всех ограничений.

множества точек, где выполняются все неравенства и ограничения

Вся область первого квадранта декартовой системы координат.

Решение задачи линейного программирования всегда находится …

В направлении минимизации последнего ограничения.

В центре области допустимых решений.

За пределами области допустимых решений.

В направлении максимизации первого ограничения.

В одной из угловых точек области допустимых решений.

В процессе поиска решения задачи линейного программирования графическим методом …

Решение находят на пересечении вектора градиента и угловой точки области допустимых решений.

Решение находят на пересечении нормали к вектору градиента и угловой точки области допустимых решений.

Решение находят в центре области допустимых решений.

Решение находят в нижней точке области допустимых решений.

Решение находят в верхней точке области допустимых решений.

Градиент функции определяется как …

Вектор, координатами которого являются первые частные производные функции по всем аргументам.

Сумма аргументов функции в некоторой точке.

Произведение ее аргументов в некоторой точке.

Максимальное значение данной функции.

Минимальное значение данной функции.

Методом ортогональных преобразований.

Перед применением симплекс-метода решения задачи линейного программирования необходимо …

Привести целевую функцию к стандартному виду.

Привести неравенства ограничений к стандартному виду.

Отложить вектор градиента целевой функции на координатной плоскости.

Построить область допустимых решений на координатной плоскости.

Перед применением симплекс-метода решения задачи линейного программирования необходимо …

Левые части неравенств ограничений вначале привести к виду больше либо равно, а затем ввести добавочные переменные и сделать неравенства равенствами.

Ввести добавочные переменные и сделать неравенства ограничений равенствами.

Отложить вектор градиента целевой функции на координатной плоскости.

Левые части неравенств ограничений вначале привести к виду меньше либо равно, а затем ввести добавочные переменные и сделать неравенства равенствами.

Построить область допустимых решений на координатной плоскости.

Условием оптимальности решения задачи линейного программирования симплекс-методом при минимизации целевой функции является …

Неотрицательность всех коэффициентов строки симплекс-таблицы.

Отрицательность всех коэффициентов в ведущей строке симплекс-таблицы.

Отрицательность либо равенство нулю всех коэффициентов в строке симплекс-таблицы.

Неотрицательность всех коэффициентов в ведущей строке симплекс-таблицы.

Отрицательность всех коэффициентов в ведущем столбце симплекс-таблицы.

Условием оптимальности решения задачи линейного программирования симплекс-методом при максимизации целевой функции является …

Отрицательность всех коэффициентов в ведущей строке симплекс-таблицы.

Неотрицательность всех коэффициентов в ведущем столбце симплекс-таблицы.

Отрицательность всех коэффициентов в строке симплекс-таблицы.

Неотрицательность всех коэффициентов строки симплекс-таблицы.

Неотрицательность всех коэффициентов в ведущей строке симплекс-таблицы

Разрешающим Ведущим столбцом в симплекс-таблице называют …

Столбец, относительно которого не будет меняться базисное решение.

Столбец, содержащий “нулевые” коэффициенты.

Столбец, относительно которого будут меняться свободные переменные. ет меняться базисное решение.

Столбец, содержащий коэффициенты равные единице.

Столбец, содержащий отрицательные коэффициенты.

Разрешающим Ведущей строкой в симплекс-таблице называют …

Строку, относительно которой будет меняться базисная переменная. ое решение.

Строку, относительно которой не будет меняться базисное решение.

Строку, содержащую “нулевые” коэффициенты.

Строку, содержащую коэффициенты равные единице.

Строку, содержащую отрицательные коэффициенты.

Базисными переменными в процессе решения задачи линейного программирования называют …

Переменные, которые на данной итерации симплекс-метода принимают не равное нулю значение.

Переменные, которые на данной итерации симплекс-метода принимают равное нулю значение.

Все переменные симплекс-таблицы.

Переменные, принимающие максимальное значение.

Переменные, принимающие минимальное значение.

Источник