в каком случае задача на равновесие плоской системы сходящихся сил является статически определимой
По исследованию условий равновесия системы сходящихся сил



Задачи данного типа могут решаться либо геометрическим (графическим) способом, либо аналитическим. При решении задач геометрическим (графическим) способом необходимо придерживаться следующего порядка:
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить все активные (заданные) силы, действующие на выделенное тело.
3. Освободить это тело от наложенных на него связей, заменив их действие реакциями связей.
4. Построить замкнутый силовой многоугольник (или треугольник – если действуют три силы). При этом следует сначала сложить все заданные, а затем достроить неизвестные силы.
5. Решить силовой многоугольник (по известным элементам определить неизвестные) или, если силовой многоугольник построен в масштабе, определить искомые силы по масштабу.
При решении задач аналитическим способом рекомендуется придерживаться следующего порядка:
1. Выделить точку, равновесие которой надо рассмотреть.
2. Изобразить активные (заданные) силы.
3. Освободить точку от связей, приложив соответствующие реакции. При этом необходимо убедиться, что данная задача является статически определимой – число неизвестных величин должно быть не более двух или трех (в случаях плоской и пространственной систем сходящихся сил соответственно).
4. Направить оси координат.
5. Составить уравнения равновесия системы сходящихся сил, из которых можно найти неизвестные величины.
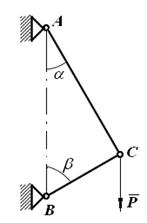
Пример.Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров (рис. 1.31). На шарнирный болт С действует вертикальная сила Р = 1000 Н.
Определить реакции этих стержней на шарнирный болт С, если углы, составляемые стержнями со стеной, равны: α = 30° и β = 60°.
Задачу можно решить либо аналитически, либо графически.
I. Геометрический способ. Очевидно, что объектом исследования в данной задаче является болт C, т.к. именно к нему приложены заданная сила 
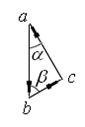
Построим замкнутый треугольник abc (рис. 1.32) для сил 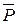
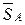
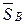
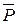
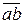
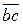
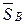
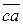
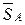
Измерив отрезки 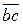
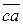
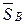
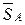
Величины неизвестных сил 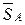
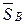
Итак, построим в масштабе вектор 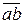
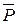
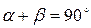
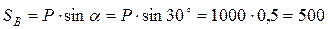
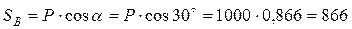
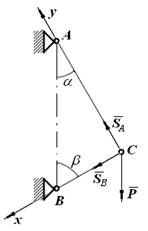
II. Аналитический способ. Выполним пункты 1-3 аналогично, как и при решении задачи графическим способом. Поэтому продолжим решение данной задачи с пункта 4 – выберем систему координат. Так как угол между неизвестными силами 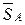
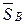
Направим Ох по линии действия 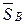
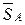
Для данной плоской системы сходящихся сил составим 2 уравнения равновесия:
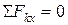
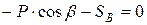
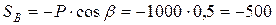
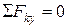
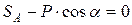
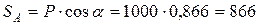
При аналитическом способе заранее неизвестно, в какую сторону направить реакции стрежней вдоль прямых АС и ВС. Если в результате решения получим положительные значения, то реакции были направлены верно, если получим отрицательные, то выбранное направление реакции изменим на противоположное.
Техническая механика
Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3 :
где FΣ – равнодействующая данной системы трех сил.
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.
Геометрическое условие равновесия плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая FΣ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.
При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Пример решения задачи
Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:
N = G tg α ; R = G/cos α
Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.
Проекция силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.
Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
Аналитический способ определения равнодействующей плоской системы сил
Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:
Направляющий тангенс угла между вектором FΣ и осью x :
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Аналитические условия равновесия плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:
Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.
Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.
Тема1.2. Плоская система сходящихся сил
§1. Геометрический способ сложения сил
Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил
(рис. 1, a), откладываем от произвольной точки О (рис. 1, б) вектор Oa, изображающий в выбранном масштабе cилу F1, от точки a откладываем вектор
, изображающий силу F2, от точки b откладываем вектор bc, изображающий силу F3 и т. д.; от конца m предпоследнего вектора откладываем вектор mn, изображающий силу Fn. Соединяя начало первого вектора с концом последнего, получаем вектор
, изображающий геометрическую сумму или главный вектор слагаемых сил:
От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное построение представляет собою результат последовательного применения правила силового треугольника.
Рис.1. Система сил
Фигура, построенная на рис. 1,б, называется силовым (в общем случае векторным) многоугольником. Таким образом, геометрическая сумма или главный вектор нескольких сил изображается замыкающей стороной силового многоугольника, построенного из этих сил (правило силового многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора
— в сторону противоположную.
Сходящимися называются силы, линии действия которых пересекаются в одной точке, называемой центром системы (см. рис. 1, а).
По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис. 1, а в точке А).
Последовательно применяя аксиому параллелограмма сил, приходим к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы
Примечания.
2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.
3. Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
§2.Равновесие системы сходящихся сил
Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.
Отсюда получаем два важных вывода:
1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».
2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил.
Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.
1. Геометрическое условие равновесия. Так как равнодействующая сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то
Плоская система сходящихся сил
Содержание:
Плоская система сходящихся сил – это система сил линии действия которых сходятся в одной точке, называются сходящимися.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Если все силы, приложенные к телу, расположенные в одной плоскости и линии их действия пересекаются в одной точке, то такая система сил носит название плоской системы сходящихся сил.
Покажем на рис. 1.6 произвольное тело, к которому приложена плоская системы сходящихся сил 



Определение равнодействующей системы сходящихся сил
Геометрический способ сложения сил:
Добавить систему сил означает определить их равнодействующую. Попробуем найти равнодействующую для плоской системы сходящихся сил, которая изображена на
рис. 1.6. Возьмем (условно) две первые силы 

статики найдем их равнодействующую 


сторонах, построим свой параллелограмм, диагональ которого, которая приложена в
точке A, и является их равнодействующей 


параллелограмм, диагональ которого будет второй равнодействующей 


Если внимательно присмотреться к геометрическому построению параллелограммов, то можно увидеть, что к концу вектора силы 




Таким образом, геометрический способ добавления сходящихся сил сводится к построению силового многоугольника. Он строится путем параллельного переноса векторов сил в масштабе, когда начало следующей силы совпадает с концом предыдущей силы. Тогда вектор равнодействующей соединяет начало первой силы с концом последней силы. Это можно записать так:
Величина равнодействующей силы не изменится, если будет изменен порядок
присоединения (добавление) сил до многоугольника, но конфигурация силового
многоугольника будет другой.
Условие равновесия плоской системы сходящихся сил в геометрической форме
Если к свободному материальному телу приложена одна сила, то о равновесии этого тела речи не может быть. Таким образом, если рассматривать плоскую систему сходящихся сил, которая сведена к равнодействующей, то тело не может быть в равновесии.
Для равновесия тела под действием плоской системы сходящихся сил необходимо и
достаточно, чтобы равнодействующая всех сил была равна нулю.
Равнодействующая такой системы сил будет равна нулю, когда силовой многоугольник будет замкнутым, то есть когда начало вектора первой силы будет совпадать с концом вектора последней силы.
Теорема о равновесии тела под действием трех не параллельных сил
Если тело под действием системы трех плоских не параллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.
Представим тело (рис. 1.7), к которому в точках А, B, C приложены силы





Далее, если есть в точке О две приложенные силы, то на основании III аксиомы статики их можно заменить одной силой, то есть равнодействующей 






Проекция силы на ось и на плоскость
Представим силу 

Обозначим сначала конце вектора силы 


По знаку проекция силы на ось тогда будет положительная, когда угол α (угол пересечения направления вектора силы или линии действия силы с осью) острый. В полной мере разумеется, если этот угол равен в 90º, то проекция силы 

Но практически тут удобнее использовать тупой угол α2, а острый угол β между вектором силы 
Таким образом, проекция силы на ось — это направленный отрезок на оси, образованный между перпендикулярами, которые опущены из концов вектора силы на ось, и который по величине равен произведению модуля силы на косинус угла между направлением вектора силы и осью.
Спроектируем теперь вектор силы на плоскость и оси координат.
Возьмем силу 




где α — угол между вектором силы 
Следует заметить, что проекция вектора силы на плоскость является вектором, потому что плоскость на имеет базисных векторов, ортов.
Если в плоскости xOy обозначить угол β, то есть возможность спроектировать силу 

В данном случае через ось z и вектор силы 
где ϒ — угол между вектором силы 
Определение силы за ее проекциями
Предположим, что у нас в плоскости рисунка имеем прямоугольную декартову систему координат Oxy, заданные две проекции силы — 


На заданных проекциях, как на сторонах, строим прямоугольник, диагональ которого, проходит через точку пересечения проекций, и является искомым вектором силы 

Углы между вектором силы 
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Аналогично для пространственной системы сил (рис. 1.9) можно построить на проекциях сила как на сторонах параллелепипед, а модуль силы 
Направление вектора этой силы также определяется через направляющие косинусы его углов с соответствующими осями координат x, y и z:
Через арккосинус определяют сами углы.
Теорема о проекции равнодействующей силы на ось
Проекция вектора равнодействующей силы на ось равна алгебраической сумме проекций векторов составляющих сил на ту же ось.
Доказательство. Имеем систему сил 




Добавим алгебраически все проекции и подсчитаем, почему эта сумма равна:
Но отрезок ak и является проекцией равнодействующей силы 
Аналитический способ добавления системы сходящихся сил
На основании теоремы о проекции равнодействующей силы на ось, имеем:
Аналогично проекция равнодействующей силы на ось y будет равняться
Модуль равнодействующей равен
Углы между вектором равнодействующей 
Зная направляющие косинусы, через арккосинус есть возможность найти сами углы.
Условия равновесия тела под действием плоской системы сходящихся сил в аналитической форме
Плоскую систему сходящихся сил можно заменить одной силой, которая носит название равнодействующей.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю. А если равнодействующая равна нулю, то и ее проекции на оси x и y тоже должны равняться нулю. Поскольку проекции
равнодействующей равны алгебраическим суммам проекций составляющих сил, то,
окончательно, иметь условия равновесия тела под действием плоской системы
сходящихся сил
Для равновесия тела, находящегося под действием плоской системы сходящихся
сил, необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси
координат были равны нулю.
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.